基于微机电系统与径向基函数的水下航行器姿态检测

张春宇, 刘福才, 程雪聪

(燕山大学 智能控制系统与智能装备教育部工程研究中心, 河北 秦皇岛 066004)

1 引 言

行为特征识别是对物体特定的动作类型或运动方式进行分类和识别,其具有很高的研究价值,是人们精准操控机器的重要条件。目前,对于物体特征识别的方法大致分为基于机器视觉识别以及基于传感器识别两大类[1]。基于机器视觉的测量技术作为一种新的非接触测量方法是以图像处理为核心[2],对视频序列中行为逐帧进行描述和识别,视觉识别处理运算量大,过程复杂,且容易受到环境因素影响。而基于传感器的识别具有成本低,体积小和不易受环境影响等优点。但高精度微机电系统(micro-electro-mechanical system，MEMS) 由于其成本高昂,目前只在航天,军工等高端领域使用,无法广泛应用于民用行业,因此对低成本传感器应用的相关研究依旧有着很重要的意义。如今中低精度的MEMS惯性传感器已被广泛应用于姿态检测系统中以获取人体的姿态信息,测量小型飞行器姿态,确定移动设备的运动状态以及步进信息等[3～5]。随着MEMS传感器的不断发展,设计小型化、低功耗、低成本、精度适中的测姿系统,使之灵活地应用于各领域成为可能[6]。

当前常用的姿态检测算法主要分为基于阈值数据处理的算法和机器学习的算法。在阈值法中,首先测量当前载体的加速度和角速度值,通过数据处理得到组合特征量,设定合适的阈值。当载体的姿态特征值超过阈值时,判断为行为变化状态;否则视为行为没有变化。由于阈值的设定存在不确定性,在不同的应用领域准确度差异性较大。近年来研究者们开始将机器学习方法引入到姿态行为检测系统中,其中包括支持向量机(SVM)[7]、随机森林[8,9]、隐马尔科夫链[10]等。作为机器学习的一种方法,人工神经网络具有自主学习性强、面对复杂数据快速寻找最优解的能力。为此,本文通过惯性传感器检测载体运动行为参数,提取行为特征向量,采用径向基函数(radial basis function，RBF)神经网络训练和构建分类模型,识别水下航行器的基本行为。

2 MEMS的数据采集与融合

将MEMS惯性传感器应用到自主水下航行器上,采用RBF神经网络算法对水下航行器的基本行为进行识别分类,整个流程如图1所示。

图1 水下航行器行为识别流程Fig.1 Underwater vehicle behavior recognition process

将MEMS惯性传感器做好防水后固定在水下航行器上,采集水下航行器在运动过程中的加速度计数据、陀螺仪数据以及陀螺仪与加速度计的数据解算得到实时的姿态角度,运用RBF神经网络对姿态检测系统采集的上述数据进行状态转换和特征提取,对提取特征后的特征值进行训练和分类,从而达到对水下航行器基本运动特征的识别。

目前,MEMS惯性器件主要包括3大类,微加速度计、微陀螺仪以及微惯性测量组合[11]。由于 MEMS 的惯性器件一般是以硅为材料,结合半导体工艺制成。它不但拥有尺寸小、成本低、功耗低、可靠性高等特点,而且环境适应性强、抗振动冲击能力高等许多优点更是其它传感器所没有的[12]。传感器采集的数据是带有噪音的,采用单传感器在对目标进行估计时,会产生较大误差且出现不稳定现象。一般需要通过对加速度传感器和陀螺仪获取的数据进行融合来实时修正系统所采集到的角度值,从而克服单传感器在姿态角测量过程中的偏差问题。基于多传感器的信息融合是一个非常重要的研究内容,只有采用适宜的融合方法才能达到最好的效果。文献[13,14]采用的加权平均法是一种简单、直观的融合方法,它将传感器信息进行加权平均的结果作为融合值,适用于动态环境,但运算精度不高。文献[15]设计了基于梯度下降法的实时姿态测量系统,并使用梯度下降算法来融合三轴加速度计IMU3000、三轴陀螺仪BMA180和三轴磁阻传感器HMC5883L的数据,完成了姿态角的测量。但梯度下降法收敛的步长对收敛性有很大影响,使用条件有所限制。

在惯性测量模块中,相对于加速度计,陀螺仪的精度会高一些,但是时间长了会漂移;加速度计没有明显随着时间增加的漂移，但其精度不高且对噪声过于敏感。在MEMS惯性传感器的数据融合算法中最为常见的莫过于卡尔曼滤波,卡尔曼滤波算法是一个最优化自回归数据处理算法,在大多数应用场景下都能够提供最优的解法。该算法的基本思想是采用递推的计算形式,即根据前一时刻的估计值和当前时刻的测量值,以最小均方差的最优估计原则,得到当前时刻的估计值[16]。 卡尔曼滤波算法最大特点就是可以实时地对状态量进行动态估计,并利用递推算法,根据新的观测量对状态量的先验估计进行校正,从而提高滤波器的性能。根据卡尔曼滤波原理,构建系统状态方程和测量方程:

Xk=FXk-1+Buk+wk

(1)

Zk=HXk+vk

(2)

式中:Xk为当前系统状态矩阵;Xk-1为上一时刻系统状态;F为状态转移模型矩阵;uk为系统控制输入,B为控制输入模型矩阵;wk为过程噪声;Zk为系统观测值;vk为测量噪声;H为观测模型矩阵,作用是将系统真实状态空间映射到观测空间。过程噪声和测量噪声皆符合均值为0,协方差分别为Q和R的高斯分布。

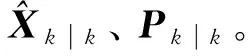
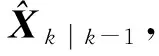
(3)

Pk|k-1=FPk-1|k-1FT+Qk

(4)

(5)

Sk=HPk|k-1HT+R

(6)

计算卡尔曼增益Kk:

(7)

(8)

Pk|k=(I-KkH)Pk|k-1

(9)

卡尔曼滤波在数据融合中被广泛应用,它属于贝叶斯滤波的一种,在MEMS惯性传感器融合中通常将陀螺仪数据作为预测,加速度数据作为观测数据,进而得出更完整的,一致的姿态角的状态估计。

本文采用集成三轴加速度计与三轴陀螺仪于一身的JY901来获取水下航行器在各个状态下的加速度值、角速度值以及解算后的姿态角,将MEMS惯性传感器安装固定在水下航行器的质心位置。根据分析水下航行器的运动特点,本设计数据采集频率设置为20 Hz。通过对照视频录像与采集数据的绝对时间来对各类状态的数据进行收集,每类行为的数据量为50组。

3 数据特征提取与RBF分类器实现

3.1 数据采集与特征提取

一般来讲,RBF网络需要的输入具有固定的格式,而MEMS传感器采集到的数据是1组数据流,因此需要将数据流分割成固定格式的数据窗,作为RBF网络的输入。目前主要使用重叠的滑动分割窗来分割数据。滑动分割窗的重叠率是1个需要结合系统延迟、算力需求和计算功耗等因素综合考虑的超参数。大部分研究人员通常会使用25%～75%的重叠率[17]。图2是使用重叠率为50% 的滑动分割窗分割加速度数据的示意图。假定1个滑动分割窗的长度为60个采样点(按20 Hz的采用频率计算,1个滑动分割窗的时间长度为3 s),第1个滑动分割窗的采样范围是从第1个采样点到第60个采样点。由于滑动分割窗的重叠率为50%,第2个滑动分割窗的采样范围是从第31个采样点到第90个采样点,生成2个滑动分割窗的时间一共为4.5 s。

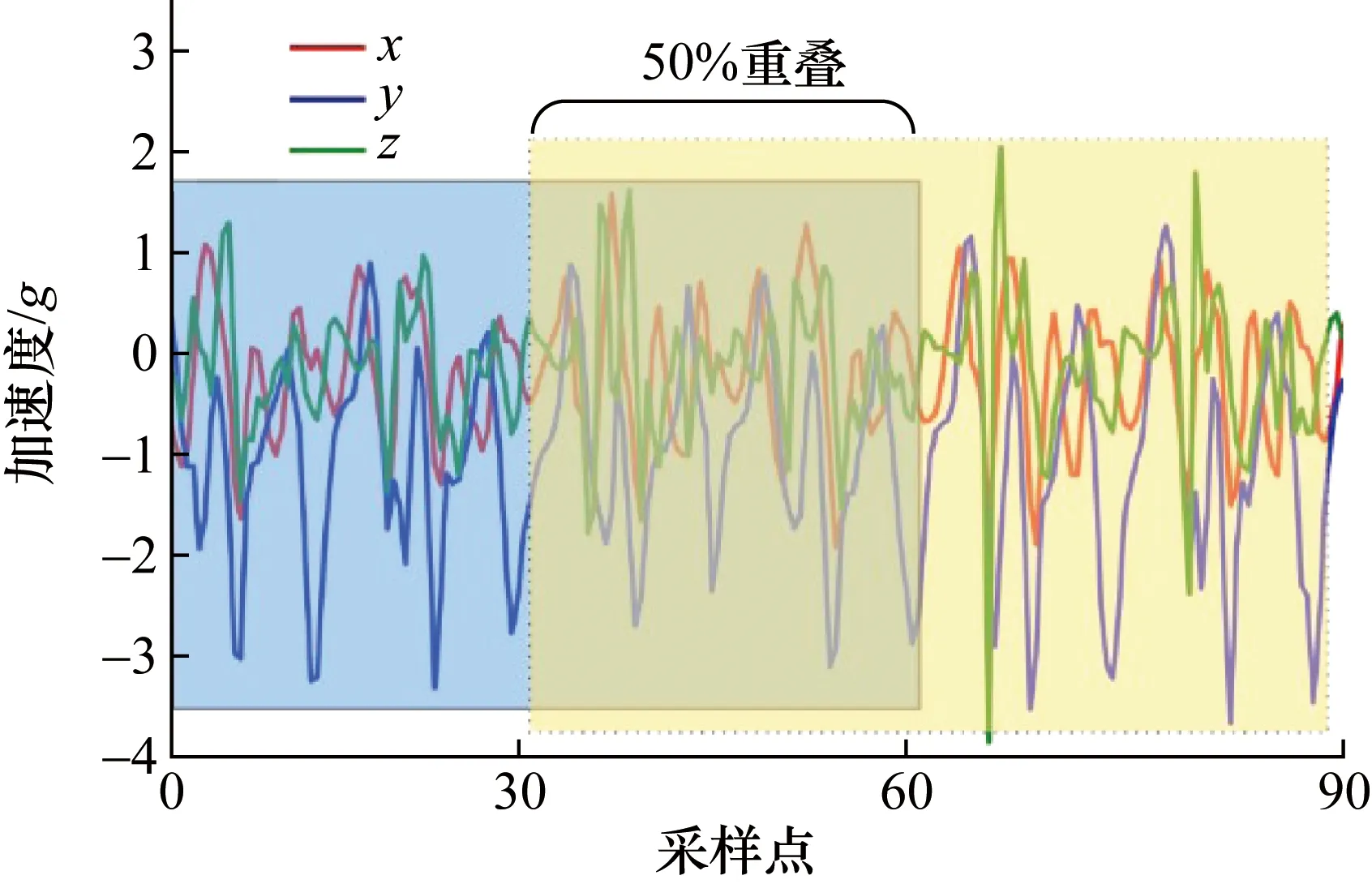
图2 滑动分割窗分割数据Fig.2 Sliding segmentation window to segment data

特征提取方法主要包括时域特征提取和频域特征提取[18,19],本设计主要提取的时域特征和频域特征特征主要为均值、标准差、最小值、最大值、众数、范围(一个窗口内最大值与最小值的差)、直流分量、幅度和功率谱密度等。

3.2 RBF神经网络分类算法

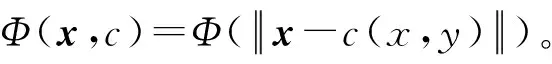
RBF可以看作是一个高维空间中的曲面拟合(逼近)问题,学习是为了在多维空间中寻找一个能够最佳匹配训练数据的曲面,然后来一批新的数据,用上述训练的曲面来处理(比如分类、回归)。RBF的本质思想是反向传播学习算法应用递归技术,这种技术在统计学中被称为随机逼近。RBF里的basis function(径向基函数里的基函数)就是在神经网络的隐单元里提供了提供了一个函数集,该函数集在输入模式(向量)扩展至隐空间时,为其构建了一个任意的“基”。这个函数集中的函数就被称为径向基函数。很明显,RBF属于神经网络领域,所以像很多神经网络一样,其结构由输入层、隐含层和输出层3层组成[17]。RBF神经网络结构如图3所示。

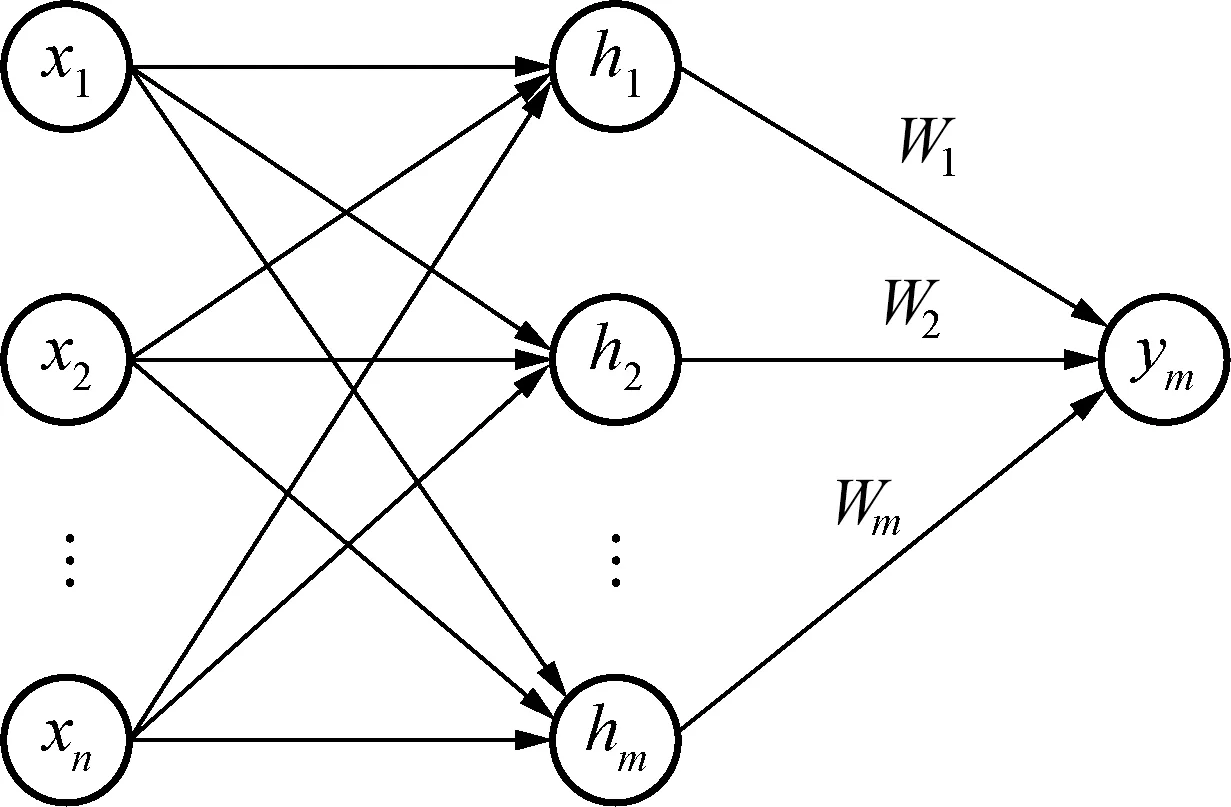
图3 RBF神经网络Fig.3 RBF neural network

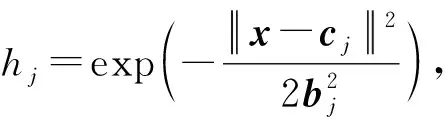
RBF分类器的实现主要分训练阶段和测试阶段2个阶段。其中训练过程主要分为2步: 1) 无监督学习阶段:确定输入层与隐含层的连接参数bij和cij;2) 有监督学习阶段:确定隐含层与输出层权值Wij。

在RBF网络的训练中常用的方法为梯度下降法,具体如下:

1) 根据提取的特征和预期结果确定输入向量x=[xi]T、输出向量y=[yi]T以及期望输出o=[oi]T;

2) 初始化隐含层中各神经元的中心参数cij、宽度向量bij和隐含层与输出层连接权值W=[W1,W2,…,Wm]T;

3) 根据实际输出y=[yi]T与期望输出o=[oi]T,采用梯度下降法,中心值宽度和输出权重等参数通过自适应学习调节到最佳值。

实验中应用 RBF 神经网络构建分类模型。首先,根据输入的训练样本以及随机产生的数据中心值和宽度计算隐含层输出值；然后，将实际输出与期望值的差值作为计算误差与设定的标准误差ε进行比较,并通过5类训练样本寻找满足误差要求的最佳模型参数。如果不满足设定的误差要求,则进行下一轮训练;一旦满足误差要求,则保存模型参数。RBF分类器工作流程如图4所示。

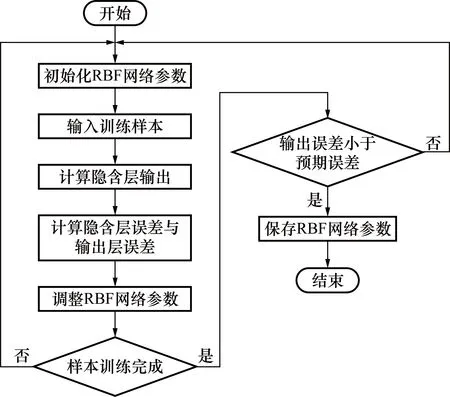
图4 RBF分类器工作流程Fig.4 RBF classifier workflow

4 数据处理与实验验证

4.1 行为的数据处理

本文将水下航行器的状态分为5类,分别为静止、前行、左转、右转和调头。每类的数据量为50组,又将各类的数据分为训练数据和测试数据,其中每类训练数据为30组,测试数据为20组。

对采集到的右转、左转、调头和前行的MEMS数据进行处理,如图5～图8所示。图5为在水下航行器进行右转时MEMS三轴加速度、三轴角速度以及z轴角度值,由图5可见在水下航行器右转过程中x、y轴加速度以及z轴的角速度变化明显,而z角度的变化也可明显判断左转(MEMS传感器设定右转为z轴角度减小,角度的变化范围为180°,在超出范围是会循环的,如图5(c)所示)。

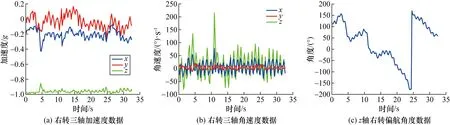
图5 水下航行器右转数据Fig.5 Right turn data of underwater vehicle

图6为水下航行器进行左转时MEMS三轴加速度、三轴角速度以及z轴角度值,由图6(b)可见在水下航行器右转过程中z轴的角速度变化最为明显,x、y轴加速度有略微变化,而z角度的变化也可明显判断左转(MEMS传感器设定左转为z轴角度增大)。

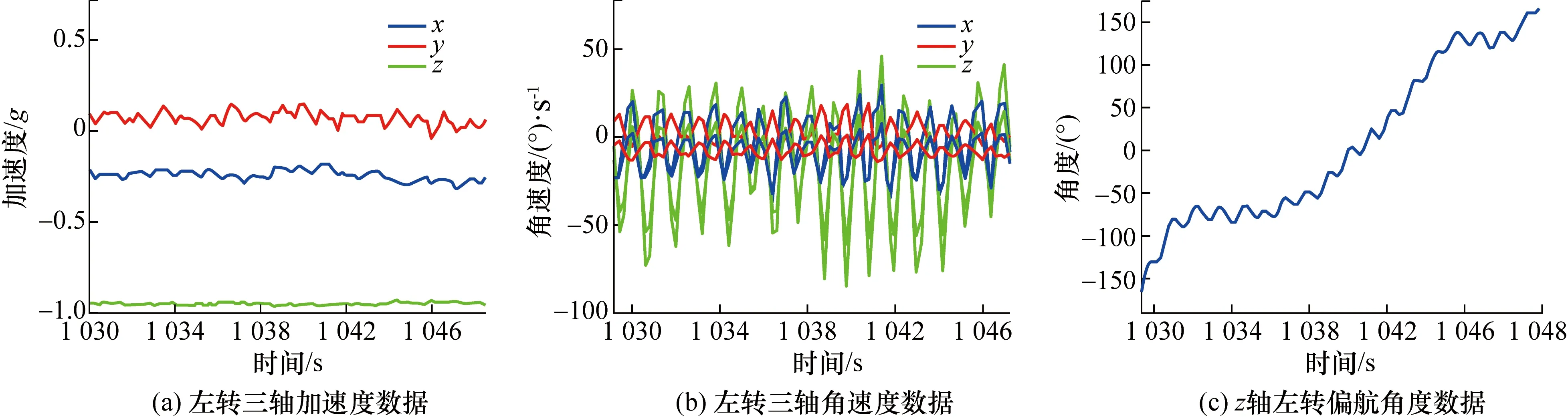
图6 水下航行器左转数据Fig.6 Left turn data of underwater vehicle

图7为水下航行器进行调头时MEMS三轴加速度、三轴角速度以及z轴角度值,由图7可见在水下航行器调头过程中传感器的各个数据变化都要比左、右转弯时幅值大。

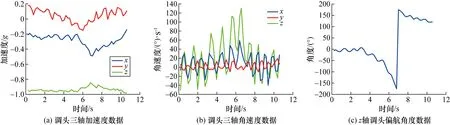
图7 水下航行器调头数据Fig.7 Underwater vehicle U-turn data

图8为水下航行器直行时MEMS三轴加速度、三轴角速度以及z轴角度值,由图8可见在水下航行器直行转过程中传感器的各个数据变化都比较稳定。

图8 水下航行器直行数据Fig.8 Straight travel data of underwater vehicle

由于实验用水下航行器运动机制类似于仿生鱼,在所有运动的过程中均是左右摆动前行的,在图5～图8中z轴的角速度以及z轴的角度变化得以体现,两者皆以类似正弦规律变化。那么在所有的动态过程都会有小幅度的左右转的现象。所以在数据提取中,以一定时间内转动超过20°的动作定义为左、右转行为。而后再根据加速度、角速度以及角度的特征加以分类。

由于本文设计主要是判断水下航行器在平面的行为,为了减少数据量过于繁杂,对于采集的加速度,角速度以及解算后的角度只使用与平面运动强相关的数据进行特征提取,来降低输入量的维度,减少神经网络的复杂度。

4.2 RBF训练与测试

以召回率R作为分类有效性判别指标,它表示的是样本中的正例有多少被预测正确了。有2种可能,一种是把原来的正类预测成正类(PT),另一种就是把原来的正类预测为负类(NF),召回率的表达式为:

(10)

首先运用水下航行器直行、左转、右转、调头和静止的前30组特征值来对RBF网络进行训练,设置RBF函数的均方差的目标为0.01,扩展速度为22,最大迭代次数为500(该参数为多次尝试后识别率最高,运行速度最快的参数,再降低均方差后,即使迭代到最大迭代次数也无法满足要求,而且识别率也无法提高)。在迭代次数达到55时,满足分类器的均方差需要。本系统迭代次数与误差关系如图9所示。

图9 迭代次数与误差关系Fig.9 The relationship between the number of iterations and the error

在训练完RBF神经网络后,对水下航行器各项基本动作的后20组测试样本来对RBF网络进行测试,其中1、2、3、4、5分别代表水下航行器直行、左转、右转、调头和静止,其结果如图10所示。

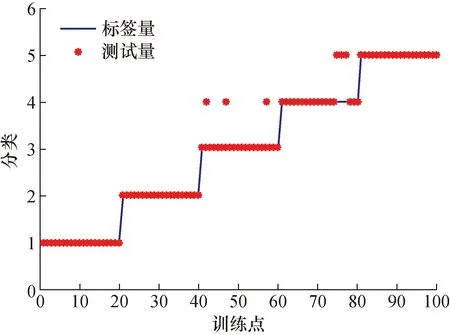
图10 RBF分类结果Fig.10 RBF classification results

系统的平均召回率为94%,其中直行的召回率为100%,左转的100%,右转为85%,调头为85%,静止状态为100%。由此可见,分类器在对右转状态和调头状态进行识别时,容易与其它状态混淆,分析原因一是特征提取不够完善，二是对于RBF函数的参数选取还需继续优化。其余状态的RBF分类器识别的召回率都比较高，可达到准确识别。

5 结 论

本文提出了一种基于MEMS传感器与RBF神经网络的对水下航行器进行姿态检测的方法,避免了基于视觉姿态检测方法的处理过程复杂、运算量大,且容易受到环境因素影响等缺点。以水下航行器为被测载体,实现对水下航行器直行、左转、右转、调头和静止等基本动作的识别。利用MEMS惯性传感器采集水下航行器在运动过程中的加速度、角速度以及解算后的角度,作为基本的采集数据,对采集数据进行处理与特征提取后输入到由RBF神经网络搭建的分类器进行训练与测试。对于来自于在水下航行器运动过程中采集的运动行为数据,采用RBF神经网络分类器进行姿态识别。实验表明,系统的平均召回率为94%,其中直行的召回率为100%,左转的100%,右转为85%,调头为85%,静止状态为100%。因此,本文提出的基于MEMS传感器与RBF神经网络的姿态检测方法能够准确地识别水下航行器的基本行为。