基于3D视觉的微通道换热器定位与尺寸测量

舒子超， 曹松晓, 蒋 庆， 徐志鹏， 楼旭东

(中国计量大学计量测试工程学院，浙江杭州310018)

1 引 言

在实现微通道换热器生产自动化的过程中，产品的上下料是必不可少的环节，为引导机械臂完成对产品的抓取，需对产品进行定位并测量其尺寸[1～3]。

近年来机器视觉被广泛应用于工业生产领域并获得了长足的发展，通过机器视觉能够快速准确地锁定被检测对象，确认其位置并引导机械臂实现准确的抓取[4,5]。目前已存在许多机器视觉识别定位与测量的相关研究。卢清华等[6]基于机器视觉并使用了一种边界搜索拟合和动态补偿的测量方法，实现了大幅面陶瓷地砖尺寸的高精度测量；刘斌等[7]结合机器视觉，先对目标进行定位再拟合其边缘，实现了对丝网印刷版的尺寸测量；Butt S I 等[8]通过机器视觉技术对铸造模具进行定位与测量实现了铸造过程的自动化。由于上述工作都基于2D机器视觉实现，因此对于初始距离不确定的待测对象难以实现有效的距离与尺寸测量，并且测量与定位结果容易受到背景噪声的干扰。Hou B等[9]提出基于机器视觉与激光测距结合的方式，利用像素坐标与二维平面坐标的转换，有效解决了焊接机器人精准测距与定位的问题，能够不受测量距离变化的影响，但依然存在复杂背景下难以实现精确图像分割的问题。3D机器视觉的应用能够很好地解决上述的一系列问题，由于能够获得待测对象的深度信息，因此能够更有效地实现前景与背景的分割以及尺寸的测量。苗中华等[10]将图像处理技术与点云数据处理技术相互配合，实现青饲机拖车车斗的边沿识别和空间定位，但该方式对于点云信息不稳定的边沿难以实现精确定位；解则晓等[11]设计了一种线结构光视觉系统，实现了随机位姿目标对象的三维定位；Ngo N V等[12]基于三维机器视觉对2D图像特征点进行坐标变换，获取了对应的世界坐标，实现了内燃机汽缸盖孔径的精确测量。

本文聚焦于大尺度微通道换热器产品的定位与测量方法进行研究，主要存在以下研究难点：

(1) 产品成像背景复杂，且颜色与产品相近，基于二维图像对产品进行分割较为困难。

(2) 产品有多种型号，尺寸各不相同，与视觉系统的距离也会改变。

(3) 产品尺寸较大，长度最长可达3 000 mm以上，受限于相机视场角(field of view, FOV)，相机与产品的距离较大从而降低了测量精度。

(4) 产品的角点位置落在产品两侧集流管的圆弧段上，坐标信息不稳定难以定位。

针对上述问题，提出一种基于3D视觉的微通道换热器定位与测量方法。通过结合产品的2D图像信息与3D位置信息，定位产品角点二维坐标、拟合角点深度、转换得到角点三维坐标并测量产品尺寸。

2 产品定位与测量方法

2.1 方法概述

图1为微通道换热器生产线中自动上料系统，其中3D相机以俯视角度拍摄目标产品，对产品进行定位并测量尺寸。将产品相关信息传输给机械臂以实现产品的自动抓取。其中相机成像平面、产品表面、地面这三者成几乎平行的状态。为实现有效的机械臂引导，要求产品各边的测量误差<1%。另外，在实际系统应用中，由于最大产品的边长为3 200 mm左右，而相机的FOV有限，为保证相机视野完全覆盖产品并保有一定余量，需要将相机置于距离产品4 000 mm处。

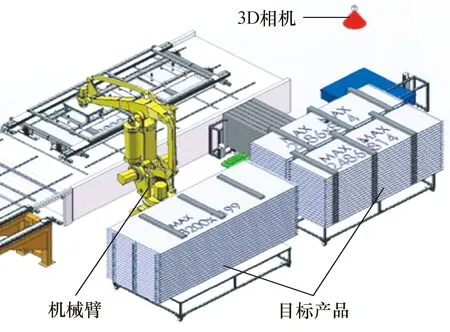
图1 微通道换热器自动上料系统Fig.1 Automatic feeding system of micro-channel heat exchangers

图2所示为微通道换热器产品，产品形状大体为一长方体，两侧各有一根圆柱形的集流管，在集流管上安装有接管座和固定片。

图2 微通道换热器产品Fig.2 Micro-channel heat exchanger products

本文所设计的定位与测量方法流程如图3所示。

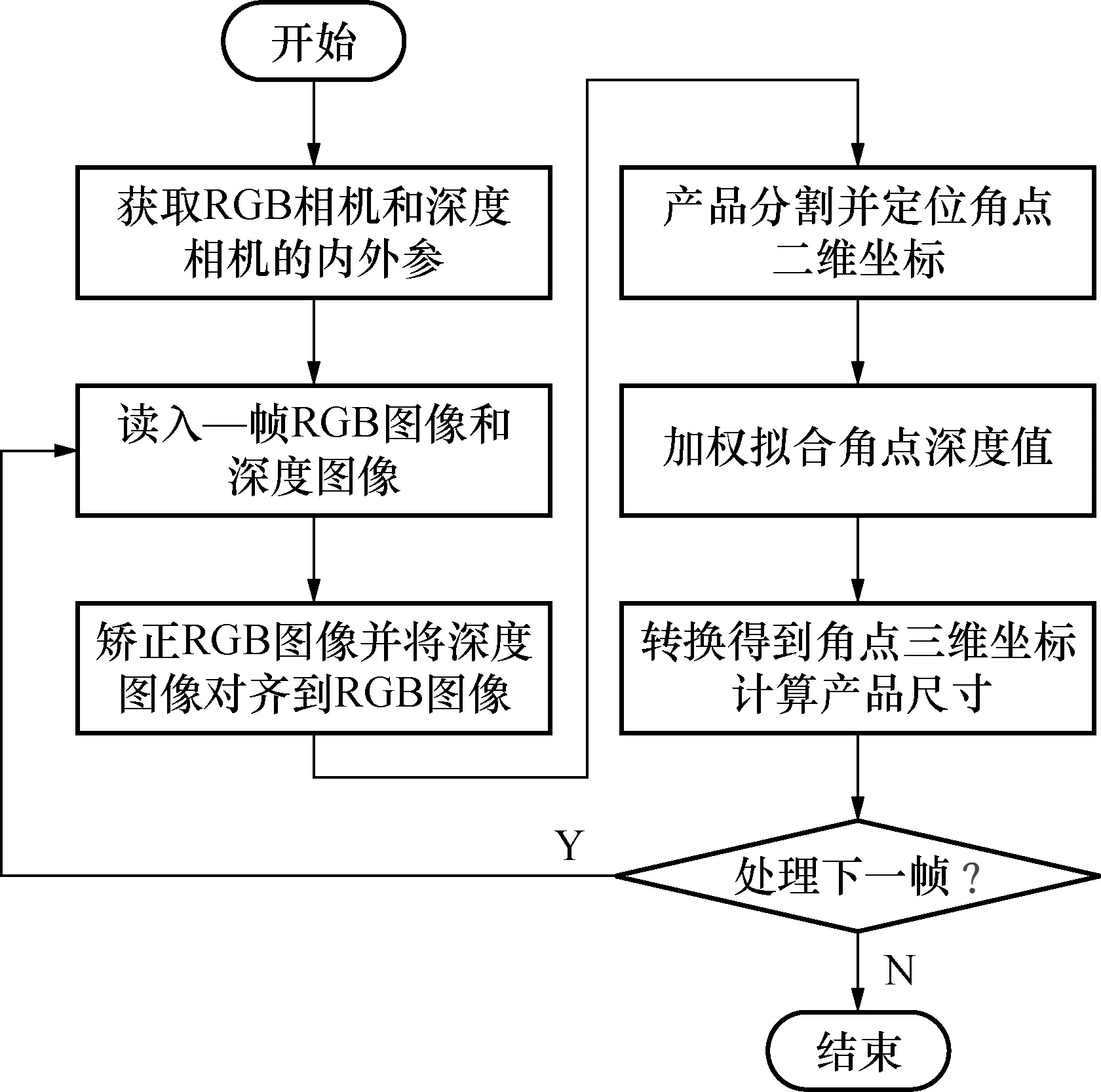
图3 微通道换热器定位与测量方法流程图Fig.3 Flow chart of positioning and measuring method for micro-channel heat exchanger

主要流程如下：

(1) 获取产品RGB-depth(RGB-D)信息，矫正RGB图像并将深度图对齐到RGB图像。

(2) 结合产品深度信息对产品进行深度下探式分割，处理得到产品轮廓并定位其角点。

(3) 选取角点近邻区域，加权拟合角点深度值。结合角点二维坐标及深度值转换得到其三维坐标，以实现尺寸测量。

2.2 图像的矫正与对齐

在处理所获取的图像前，需对图像进行矫正，并将RGB图像与深度图像对齐以便于后续的操作。对于已完成标定的相机，其内参、外参矩阵与畸变参数均已知。

由于相机制造工艺的偏差、入射光线在通过各个透镜时的折射误差和CCD点阵位置误差等，实际的光学系统存在着非线性几何失真，从而使目标像点与理论像点之间存在着多种几何畸变[13,14]。本文主要对相机的径向畸变和切向畸变进行矫正。

径向畸变的数学模型可以表示为

(1)

式中：(x,y)为正常图像位置坐标；(x′,y′)为畸变图像位置坐标；r为该点距离成像仪中心的距离；k1，k2，k3为径向畸变系数。

切向畸变的数学模型可以表示为

(2)

式中：p1，p2为切向畸变参数。

结合物理尺寸与像素点的比例因子dx、dy，就可以通过非畸变图像的坐标(u,v)求得在畸变图像上的坐标(ud,vd)。由于畸变图像已知，从(ud,vd)坐标处得到所需像素值，采用插值处理得到非畸变图像。

在相机的内参与外参矩阵已知时，RGB图像与深度图像对齐可以通过矩阵变换实现[15]。像素坐标系与世界坐标系的转换关系如下：

(3)

式中：zc为(u,v)点深度值，M1为相机3×3的内参矩阵，M2为相机3×4的外参矩阵，(xw,yw,zw)为该点的世界坐标。

图像对齐的坐标转化公式如下：

(4)

式中：Pc、Pd分别为某点在彩色图像坐标系和深度图像坐标系下的二维点坐标向量；Tw2c，Tw2d分别为世界坐标系转换到深度摄像头和彩色摄像头坐标系的外参矩阵；Kc，Kd分别为深度摄像头和彩色摄像头的内参矩阵。

通过上述公式可以将深度图中的二维点映射到RGB图像中，实现图像的对齐。

2.3 产品分割与角点二维定位

由于产品角点位于两侧集流管的圆弧段上，因此三维坐标信息不稳定。为提高产品角点的三维定位精度，本文提出先在二维图像中分割出产品轮廓，锁定角点，再结合深度值进行坐标转换得出角点三维坐标的定位算法。

图像分割的精度很大程度上决定了角点的定位精度。由于产品待测表面几乎与相机成像平面平行，且检测区域内不存在与产品待测表面同深度的大体积干扰物，因此本文利用产品3D信息的辅助，采用深度值下探式的图像分割方法对产品图像进行分割：

(1) 设置一定的深度初始值x0，设定检测区间Δl。

(2) 分割出深度图中深度值处于(x0,x0+Δl)区间内的像素点。

(3) 若得出点的数量超过一定阈值，则认为已到达工件表面，停止下探。保存分割出的像素点为像素值255，其余点像素值为0。若得出点的数量未满足阈值，则将x0增加Δx，回到步骤2继续循环下探检测。

得到产品的初步分割图像后，为平滑图像边缘并消除产品接管座对轮廓提取的影响，先采用高斯滤波对图像进行平滑[16]，其次需要对图像进行形态学操作以进一步提高图像边缘的定位精度，其中主要包括膨胀、腐蚀、开运算与闭运算[17]。若原始图像为f(x,y)其定义域为Df，高度为0结构元素为E(x′,y′)定义域为De。

膨胀后的图像g(x,y)可表示为

g(x,y)=f⊕E=max{f(x-x′,y-y′)}

(5)

腐蚀后的图像g′(x,y)可表示为

g′(x,y)=f⊗E=min{f(x-x′,y-y′)}

(6)

式中： (x-x′,y-y′)∈Df， (x′,y′)∈De。

开运算可表示为

f∘E=(f⊗E)⊕E

(7)

闭运算可表示为

f·E=(f⊕E)⊗E

(8)

本文中先采用一个3×3的矩形结构元素对高斯滤波后图像进行闭操作，以去除图像中的无效深度点；再用7×7的矩形结构元素进行开操作，以去除与目标产品同深度的干扰物的影响；最后分别采用20×1和1×20的矩形结构元素进行开操作，由于产品几乎为一个规则的矩形并且绕z轴旋转角度不大，因此该操作不仅能保留工件分割图像的几何特征，还能消除接管座和固定片对产品轮廓的影响。

获取形态学处理后图像的轮廓，寻找轮廓的最小外接旋转矩形并获得旋转矩形的4个顶点坐标，认定这4个坐标为产品角点的二维坐标。

2.4 产品角点的深度拟合

为转换得到产品角点的三维坐标，还需获取角点的深度值，由于产品角点的空间位置信息不稳定，因此无法直接获取角点的有效深度。本文采用近邻区域加权拟合的方式进行精确估算，由于集流管附近的工件表面为平面，深度信息较为稳定，且深度值与角点相近，因此可为获取角点深度提供参考。如图4所示红色点为工件实际角点，蓝色区域为角点深度参考区域。

图4 产品角点与深度拟合区域Fig.4 Product’s corner and depth fitting area

参考区域内与角点距离越近的点参考价值越高，将区域内所有点的深度值加权求平均以获得角点的等效深度d，计算方式如下：

(9)

式中：n为参考区总点数；pi为参考点的权重，i表示参考区域内的第i个像素点；di为参考点的深度；Δxi，Δyi分别为参考点与角点的横纵坐标差值。

在实际计算中为减少计算量，可将公式(9)等效为

(10)

图5所示为产品成像示意图，p为产品角点，h为产品厚度，计算所求角点等效深度值d并非是真实深度，为得到真实深度d′需进一步转化：

图5 产品成像示意图Fig.5 Schematic diagram of product imaging mode

(11)

2.5 产品角点三维坐标的转换及尺测量

为转换得到产品角点的三维坐标，将公式(3)中的相机内外参矩阵展开，可以得到深度相机的坐标转换表达式：

(12)

式中：f为相机焦距；dx、dy为比例因子；R，T为相机外参矩阵中的旋转矩阵和平移矩阵。

将世界坐标系的原点设置在与相机光心同一位置处，即有：

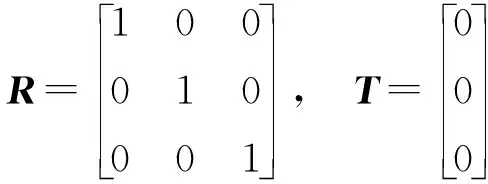
(13)

将式(13)代入(12)得到表达式：

(14)

相机的内参为定值，因此在已知角点深度图二维坐标(u,v)和角点深度值zc的情况下，即可换算得到角点的世界坐标。

若求得两角点世界坐标分别为(x1,y1,z1)和(x2,y2,z2)，则对应产品边长尺寸可表示为

(15)

3 实验及结果分析

实验采用RGB-D相机，工作距离为1 280～5 000 mm，深度分辨率为1 280×960，RGB分别率为2 592×1 944，X、Y方向的FOV为56°×45°，相机标定参数如表1所示。

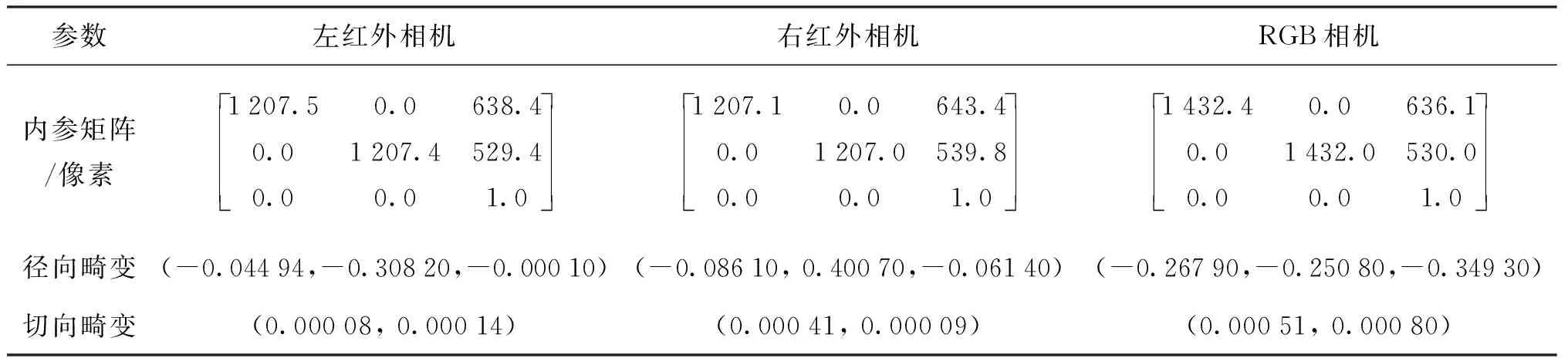
表1 相机标定参数Tab.1 Camera calibration parameters

图6为矫正畸变前后的RGB图像。实验所用的微通道换热器样品为某公司微通道换热器实际生产线中的目标产品。

图6 矫正前后的RGB图像Fig.6 RGB images before and after correction

3.1 角点定位实验结果与分析

图7为产品角点二维定位的流程。

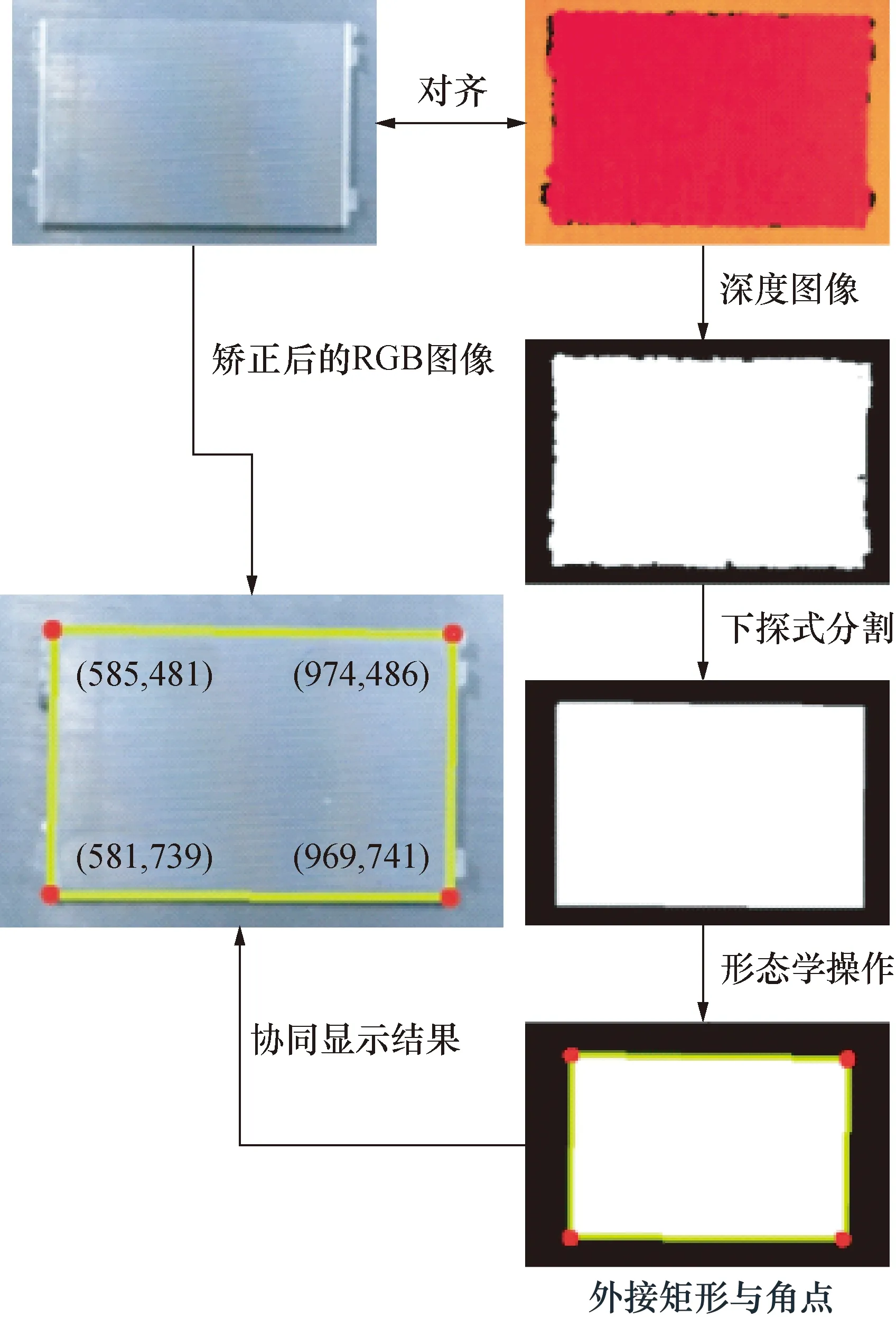
图7 角点二维定位流程Fig.7 Two-dimensional positioning process of corners

在协同显示图中，角点的位置为二维像素点的坐标。定位角点的二维坐标后，结合深度图采用邻近区域加权拟合的方式估计角点的深度，分别对两个型号产品的8个角点深度值各进行20次测算，实验结果见表2。

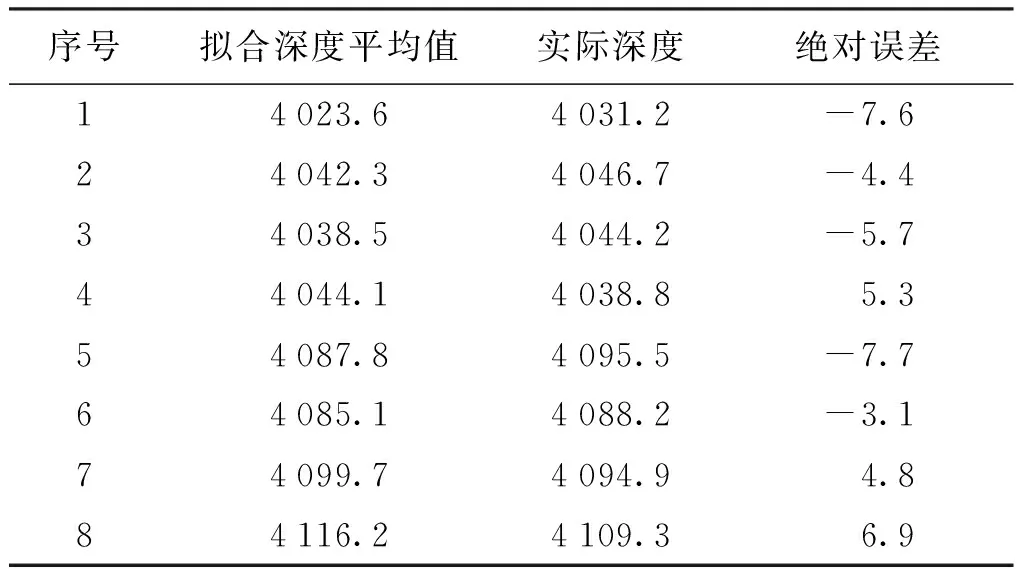
表2 深度测量结果Tab.2 Results of depth measurement mm

在8个实验点中，误差的绝对值最大为 7.7 mm，而本文采用的相机在4 000 mm的测量距离时本身具有±5.2 mm的测量误差。因此本文的深度拟合方法对角点的深度估计较为准确，且所得结果稳定。

3.2 尺寸测量结果与分析

结合相机的内外参矩阵，通过产品角点的图像坐标与深度值换算得到其三维世界坐标，设世界坐标原点与相机光心重合。由勾股定理计算产品的长宽。对两个产品进行尺寸测量，其中小产品实际尺寸为1 208×809 mm2，大产品实际尺寸为 2 956×1 615 mm2。

图8为产品尺寸测量可视化的结果，角点的三维坐标与产品长宽已在图中标出，单位均为mm。

图8 测量结果显示Fig.8 Visualization of measurement results

为验证本文图像分割算法的有效性，以及尺寸测量算法的准确性，在测量距离为4 000 mm时对小产品的两条边长分别进行20次重复测量实验并得出结果。设置对照组：采用Grabcut二维图像分割算法，提取RGB图像的前景后滤除接管座和固定片并锁定其角点，直接读取深度图中角点对应的深度值，转换得到角点世界坐标以实现尺寸测量。图9为滤除接管座和固定片后的图像分割结果对比，相较于常规的二维图像分割算法，由于本文图像分割算法利用了产品的3D信息进行辅助，因此能够更精确地从复杂的背景中分离出前景。尺寸测量结果对比如表3所示。

图9 图像分割结果对比Fig.9 Comparison of image segmentation results

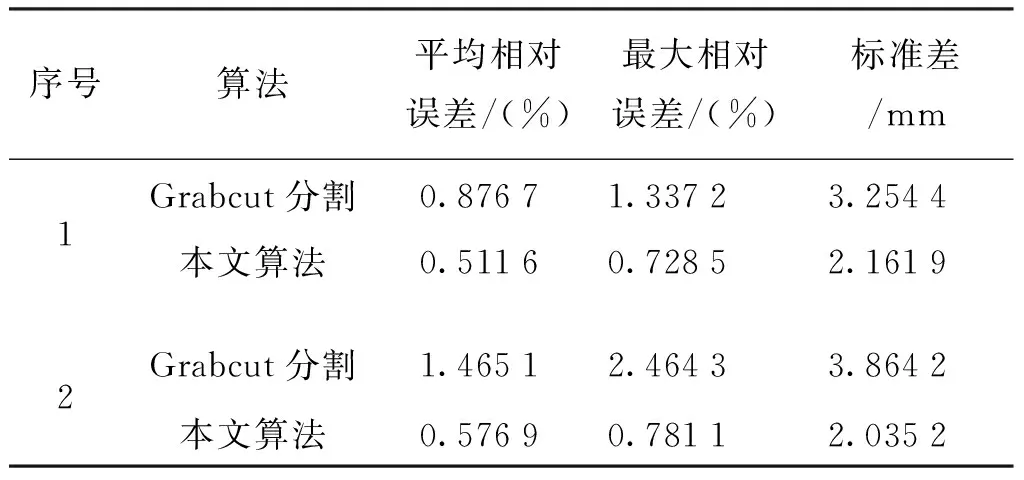
表3 尺寸测量结果对比Tab.3 Comparison of dimension measurement results

表3中：序号1表示产品较长边，参考真值为1 208 mm；序号2表示产品较短边，参考真值为809 mm。从实验结果中可以看出，本文算法与Grabcut分割算法相比较，尺寸测量值在平均误差、最大误差与标准差均有所减小，并且最大误差<1%，满足系统需求。

改变测量距离，使用本文算法对两个型号微通道换热器进行尺寸测量实验，以验证算法在工作距离不同时的测量精度。统计不同工作距离下各边长的相对测量误差并求取平均，得出的实验结果如图10所示。在相机分辨率固定不变时，尺寸测量的误差随着测量距离的增加总体呈上升趋势。其中较长边测量的误差较小，且随测量距离的增大上升趋势不明显，而较短边的测量误差较大，且随距离的增大出现较为明显的上升；另外，对于3 500～4 500 mm的工作距离，相机在X、Y方向上本身具有8.01～10.19 mm的测量误差。这表明在不同测量距离能够实现较为稳定的尺寸测量。

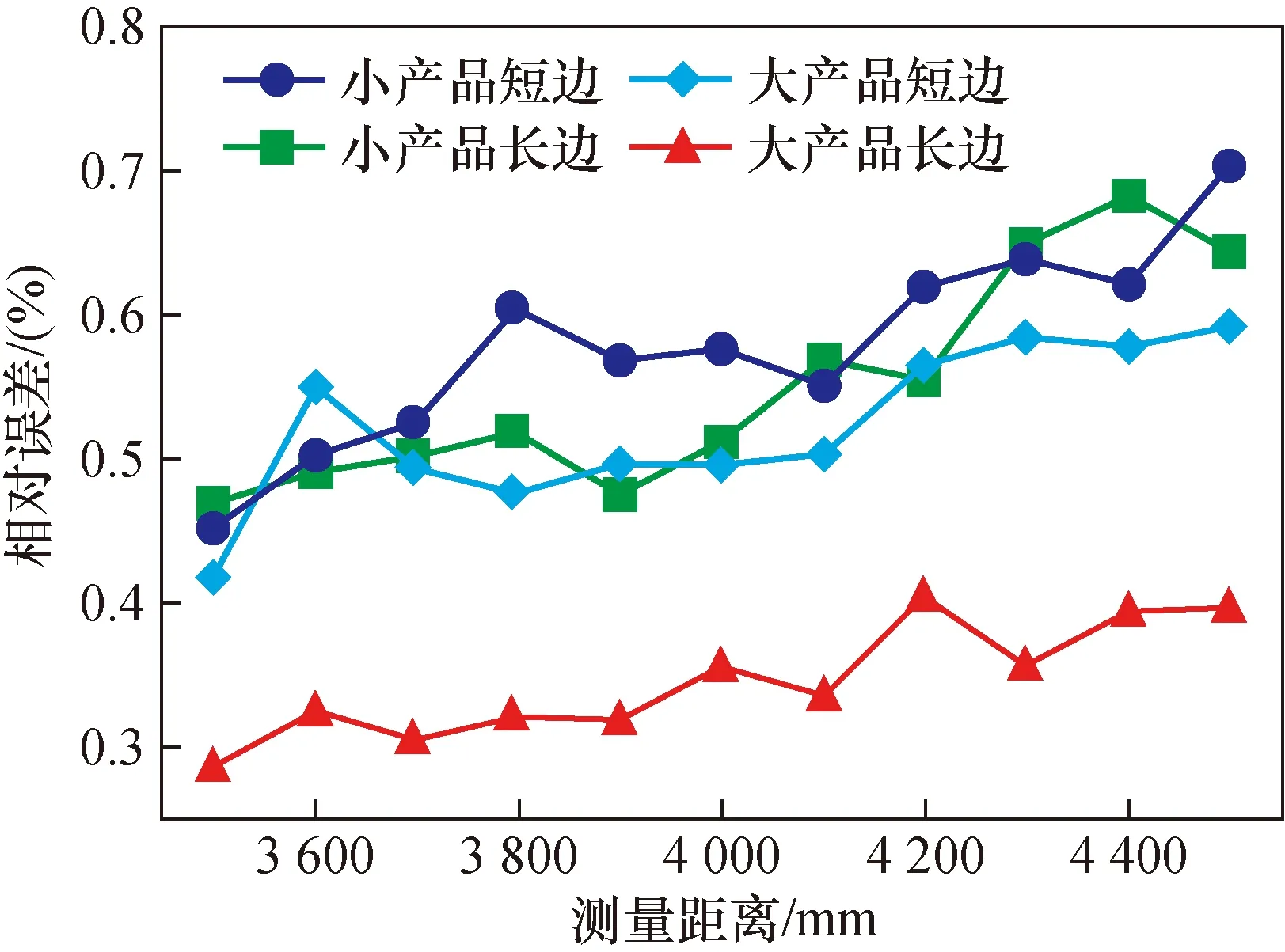
图10 测量相对误差分析Fig.10 Analysis of relative error in measurement

4 结 论

本文所提微通道换热器定位与测量方法在结合待测物的2D与3D信息的同时，能够有效地将目标对象从复杂的背景中分离出来，精确地拟合角点的深度值，从而实现高精度的尺寸测量。实验数据表明，在测量距离为4 000 mm时测量误差<1%，能够作为引导机械臂抓取微通道换热器有效的参考值。

同时，本文所提算法同样能够应用于其它领域。结合更多的机器视觉技术，在复杂环境下对初始位姿不同的待测物进行定位与测量。但是由于3D相机所获取的深度信息存在一定的波动，因此所得最终测量值的重复性不理想，并且精度也有待进一步提升。设计合适的补偿算法或结合二维轮廓信息进行更精确的图像分割来提高测量的精度和重复性，这将是后续进一步的研究工作。