新课标理念下的数学教科书“综合与实践”活动：“关键特征”“基本类型”与“呈现要点”

李海东，李 健

新课标理念下的数学教科书“综合与实践”活动：“关键特征”“基本类型”与“呈现要点”

李海东，李 健

（人民教育出版社 课程教材研究所，北京 100081）

为应对创新型人才的培养需求，《义务教育数学课程标准（2022年版）》赋予了“综合与实践”活动新的内涵．数学教科书中“综合与实践”活动的编写，为新课标理念的落地提供重要保障．数学教科书“综合与实践”活动的3个关键特征为综合性、实践性、开放性．基于关键特征构建了“综合与实践”活动的三维特征模型，结合教科书编写实际情况，整合出低、中、高3种不同学生要求的基本活动类型．开发数学教科书“综合与实践”活动时，除了要把握好关键特征，还要注意一些呈现要点，包括以“问题”引领活动设置，以“过程”指导活动实施，以“评价”保证活动质量．

课程标准；数学教科书；综合与实践；跨学科

1 问题提出

随着时代发展，在生产生活中将面对大量的跨学科、综合性问题．如何培养具有解决这类问题能力的创新型人才，自然成为中国基础教育应对时代发展的重要任务．近年来，STEM教育强调的跨学科课程备受关注[1]，美国甚至将STEM教育作为维持当今美国国家创新能力的根基[2]，跨学科课程被提至美国国家战略高度，也为中国基础教育课程改革提供了良好借鉴．2016年2月，《全民科学素质行动计划纲要实施方案》明确提出：在中学阶段要增强学科间横向配合，开展跨学科实践探究活动．而在《教育信息化“十三五”规划》《关于加强和改进中小学实验教学的意见》等文件中，也均提及跨学科学习、多学科融合教育等要求．在此背景下，如何更好地推动跨学科课程落地，无疑成为中国新一轮课程改革的重要发力点．

2022年4月，新颁布的《义务教育课程方案（2022年版）》要求：各门课程用不少于10%的课时设计跨学科主题学习[3]．而在《义务教育数学课程标准（2022年版）》（简称《标准（2022年版）》）中，以跨学科主题学习为主的“综合与实践”，与“数与代数”“图形与几何”“统计与概率”共同构成义务教育阶段数学课程内容的4个学习领域．《标准（2022年版）》指出：“综合与实践”以培养学生综合运用所学知识和方法解决实际问题的能力为目标，重在解决实际问题，以跨学科主题学习为主，主要包括主题活动和项目学习，等等[4]．

教科书是桥接课程标准与课堂教学的中间课程形态．长久以来，数学教师对教学内容的把握、教学策略的选择，主要受到数学教科书的直接影响[5–6]．与常规教学内容相比，大多数数学教师对于《标准（2022年版）》要求下的“综合与实践”活动并不熟悉，甚至比较陌生．对于数学教科书中的“综合与实践”活动这一教学资源，教师们需求紧迫、依赖性强．因此，开发高质量的数学教科书“综合与实践”活动，成为新课标理念下“综合与实践”有效落地的重要保障之一．基于新课标理念与教科书编写实际，对数学教科书“综合与实践”活动的关键特征、基本类型与呈现要点进行讨论，可以为《标准（2022年版）》理念下“综合与实践”领域的教科书编写提供参考，帮助一线教师全面认识“综合与实践”活动，使其获得更多适合自主开发和用于自身教学的高质量“综合与实践”活动的经验．

2 “综合与实践”活动的关键特征

开发数学教科书的“综合与实践”活动，必不可少地，要对其关键特征有一个清晰认识．基于影响教科书质量的重要因素[7–8]，以及《标准（2022年版）》对“综合与实践”领域的定位，在数学教科书的具体开发过程中，相比于常规内容的编写，“综合与实践”活动的编写必须重点关注：如何处理好不同学科内容间的综合？如何使学生获得良好的活动实践？如何使活动设置更好地满足不同类型的教学需求？基于上述3个关注点，得到数学教科书“综合与实践”活动的3个关键特征：综合性、实践性、开放性．

2.1 综合性

相比于《义务教育数学课程标准（2011年版）》中的“综合与实践”活动，《标准（2022年版）》对“综合”一词的界定更加宽泛：不仅可以是数学与日常生活间的紧密联系，还可以是数学与其它学科间的关联[4]．在此，将“综合与实践”活动的综合性定义为学生完成活动过程中，数学与日常生活或其它学科知识所起作用的关联．

讨论综合性之前，必须要认识哪些对象可以与数学学科进行综合．除了可以将数学与日常生活相关联，《标准（2022年版）》中还有将数学与科学、技术、经济、金融、地理、艺术等学科领域相融合的提法[4]．在STEAM教育理念中[9]，与数学相综合的学科可分为科学、技术、工程、艺术等学科领域，每个领域下又可细分下属学科，如科学学科领域下的物理、化学、生物等，艺术学科领域下的美术、舞蹈、音乐等．由此可见，数学可以与类型广泛而多样的大多数学科相综合，体现出“综合与实践”活动选材的广泛性．

关于如何将不同学科进行综合，需要考虑如何处理同一活动所涉不同学科的学科地位．目前，中国跨学科课程主要分两类：基于学科渗透的相关课程模式，基于学科融合的广域课程模式[10]．两种模式的主要区别在于对主体学科的定位，前者有单一的主体学科，后者将多门学科作为联合主体．在以数学作为单一主体学科的“综合与实践”活动中，日常生活或其它学科主要充当着为活动提供问题情境的角色，对于问题的解决并不起过多作用；而在广域课程模式下的“综合与实践”活动，其问题解决需要不同学科知识共同作用、有机结合，更有可能体现出较强的综合性．

2.2 实践性

“实践”是指人们有意识地从事改造自然和改造社会的活动，所谓实践出真知、实践是检验真理的唯一标准，无不体现出实践对于人类发展的重要性．“综合与实践”活动的实践性，指完成活动过程中，需要学生亲身经历的思维过程或行为表现．数学教科书“综合与实践”活动的实践性的体现，需要学生把认知与行动、理论与实践、数学知识与其它学科知识有机融合，为落实数学课程总目标提供了保障．

学科实践活动是学生形成核心素养的重要路径[11]．《标准（2022年版）》指出数学课程要培养的学生核心素养包括会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界[4]．观察、思考、表达这些行为动词，体现出学生在数学学习实践活动不同阶段的具体实践行为方式．因此，“综合与实践”活动的实践性，与数学核心素养的表现形式高度关联，有助学生数学核心素养养成．

对于数学教科书“综合与实践”活动的开发，不仅要关注实践活动的次数多少，更要关注活动所体现的实践性的强弱．活动实践性的强弱水平，直接影响着学生的数学活动经验发展机会，而数学活动经验又是数学基础知识、基本技能、基本思想的黏合剂．此外，《标准（2022年版）》对学生进行“综合与实践”活动的学业要求表明：学生要通过实践活动，发展发现、提出、分析、解决问题的能力，并借此在学习能力、表达能力、应用意识、创新意识等方面获得提升[4]．上述学生发展要求，指出了体现活动实践性的一些具体实践方式，例如发现、提出、分析、解决问题，以及合作交流、方案设计、制作物品等．

2.3 开放性

编写教科书时，必须谨慎应对不同学生之间的差异性．一方面，中国幅员辽阔，许多地域间的文化、经济水平存在差异，导致各地学生对相同事物的认知情况并不完全相符；另一方面，即便对于相同地域乃至同一班级的学生，由于学生的知识储备、认知能力、志趣爱好等存在差异，使得他们可能具备不同的发展需求．因此，“综合与实践”活动的开发者必须面对具有不同认知水平、不同发展意向学生的差异化需求．应对学生数学学习差异的一条重要途径即设计开放性的任务[12]，因此有必要加强“综合与实践”活动的开放性．基于已有研究[13–14]，将“综合与实践”活动的开放性定义为：在活动的条件、问题、过程、结果等环节上具有的多种可能．

“综合与实践”活动的条件与问题的开放性，可以使学生面对各式不同活动．条件的开放性，主要表现为提供给学生冗余或缺失的活动条件，要求学生自行选择或补充有用信息．问题的开放性，主要表现为可供学生选择的平行任务，或可由学生自行提出的感兴趣的研究问题等．此处讨论的条件与问题的开放性，是作为教科书文本呈现给学生的，下面讨论的活动过程与结果的开放性，则侧重于学生的实践．

在进行“综合与实践”活动的过程中，存在两个世界，一个是数学世界，另一个是与其它学科相关联的现实世界，学生要想解决问题，就要处理好数学世界与现实世界的信息互换，包括将现实世界信息抽象为数学信息，将数学信息翻译为现实世界信息[15]．因此，对于一些涉及不同领域学科信息的活动，在学生进行抽象或者翻译的过程中，过程与结果不是预先确定的，而是存在多种可能的，学生拥有的知识与能力体系越丰富，信息转化时的质量就越高[16]．此外，由于“综合与实践”活动所具备的实践性特征，使得不同学生可能产生形式各异的实践过程，这也是活动过程开放性的一种重要表现．

3 “综合与实践”活动的基本类型

在实际的教科书编写过程中，常常需要在教科书不同位置匹配上对应的“综合与实践”活动．为了将“综合与实践”活动有机融入数学教科书中，有必要根据其在关键特征上的不同表现水平，对其进行类型划分．

3.1 “综合与实践”活动的三维特征模型

数学教科书中的“综合与实践”活动在3个关键特征上的表现存在强弱差异（见表1）．

表1 关键特征的表现水平

通过对3个基本特征的强弱表现的划分，可以构建一个关于“综合与实践”活动的三维特征模型（见图1）．三维特征模型包括3个特征维度，综合性指向学科内容关联，实践性指向学生活动实践，开放性指向作为大众教学资源的教科书所应具备的应对学生学习差异的能力．在该模型中，越接近于点，表示在3个特征维度上的表现水平越弱；越接近于点，表示在3个特征维度上的表现水平越强．

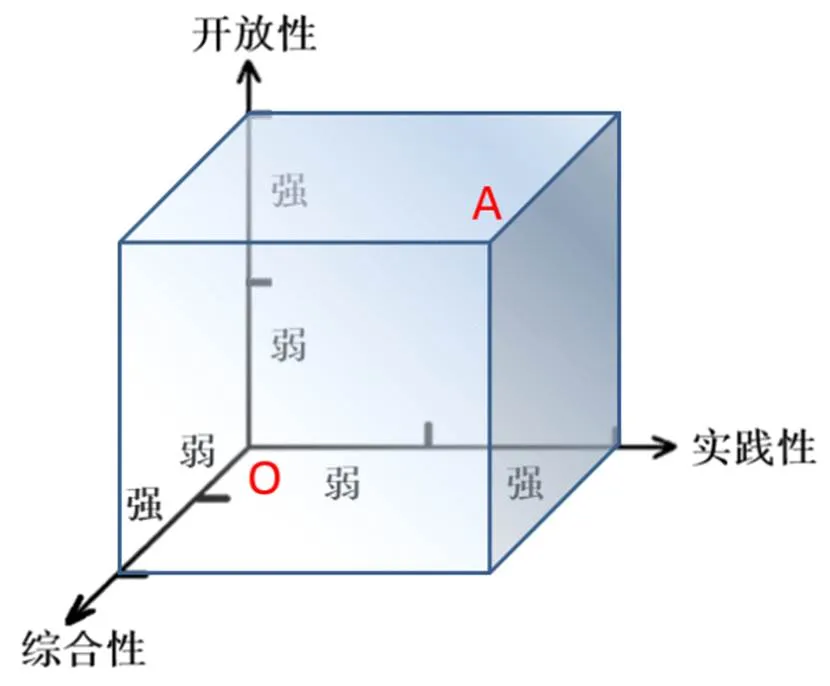
图1 “综合与实践”活动的三维特征模型

3.2 基于三维特征模型的活动基本类型划分

由于每个特征维度均具有强弱水平之分，因此基于“综合与实践”活动三维特征模型，总共有8种活动类型．为了方便起见，结合教科书编写实际情况，将8种活动类型整合为3种类型，它们分别对学生提出了低、中、高水平要求，分别记为低、中、高要求型活动．

3.2.1 低要求型活动

低要求型活动，即在3个特征维度上都具有弱表现水平的活动．例如基于第四学段“数据分析”内容设置的活动．

下表记录了3个城市在近几年的火灾发生次数，你能通过表中数据获得哪些信息？请选择合适的统计图描述表中数据，并向其他同学介绍你从图中读到的信息．

城市20162017201820192020 A2631 352840 B87881017976 C4247 505154

就综合性而言，该活动属于数学与日常生活相关联，但“3个城市在近几年的火灾次数”作为问题背景，并不直接影响学生选择与绘制统计图，对于数据的解读也无太大关联，属于典型的装饰型情境[15]．因此，该活动在此维度表现为弱综合性．

就实践性而言，该活动需要学生基于所给数据的类型与特点，选择合适的统计图并进行绘制，这对学生的思维水平或动手操作要求并不高．又由于背景信息对问题的影响强度不高，所以学生对所绘统计图的解释说明也并不困难．因此，该活动在此维度表现为弱实践性．

就开放性而言，由于学生可以根据自身对活动的理解，选择并绘制不同类型的统计图，并且不同学生对统计图的解释说明也可能因人而异，仅表现为活动过程与结果的不唯一性．因此，该活动在此维度表现为弱开放性．

综上，该活动表现为弱综合性、弱实践性、弱开放性，属于低要求型活动．通常而言，这类活动的综合难度系数不大，学生完成活动的耗时不长，比较适合在教科书的知识引入与训练系统（包括例题、习题）中使用．

3.2.2 中要求型活动

中要求型活动，即在一或两个特征维度上具有弱表现水平，在其余维度上具有强表现水平的活动．例如基于《标准（2022年版）》中的活动实例“图画还原”[4]所开发的活动．

图像复原技术在恢复老旧照片、景象识别等领域有较强应用．用数学语言准确地表达出图像的复原方式，有助我们了解图像复原过程中的具体过程．让我们应用已学知识，一起来完成一些简单图形的复原吧！首先，请利用平移和旋转将下方右图还原为左图，并记录还原的步骤．其次，尝试将一幅你喜欢的美术作品进行网格切割，再打乱顺序，然后选择一种操作步骤最少的方式将其还原，并记录步骤．

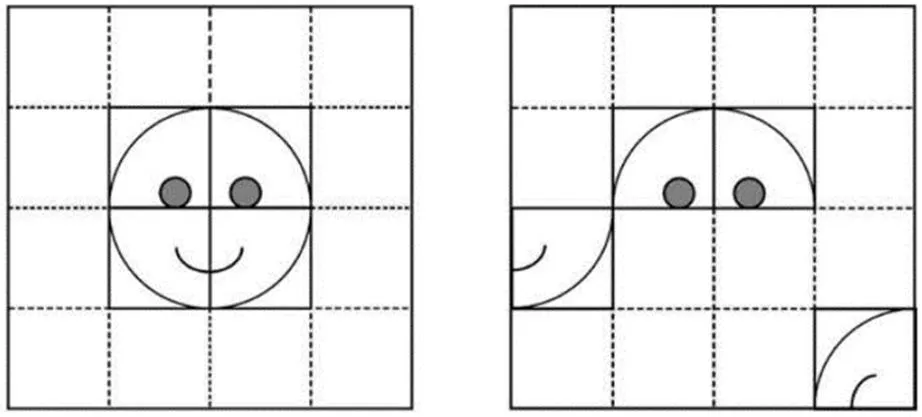
就综合性而言，该活动将数学与计算机科学领域的图像复原技术、艺术领域中的美术作品结合，但问题解决的过程与图像复原技术、美术作品的特性并无实质性关联，即问题解决过程不需要非数学领域知识．因此，该活动在此维度表现为弱综合性．

就实践性而言，该活动需要学生将美术作品按一定方式打乱顺序、还原图案、记录操作步骤最少的还原方式等都属于实践性活动．对于学生而言，图案的还原过程以及记录还原步骤都并不复杂；而选择一种操作步骤最少的还原方式，即该活动的最优解，则需要学生经历反复尝试、比较、归纳等活动过程，具有一定的实践挑战性．因此，该活动在此维度表现为强实践性．

就开放性而言，该活动需要学生自行选择一幅美术作品打乱顺序，再将其还原以及记录还原步骤，这需要学生自行设定活动条件．因此，该活动在此维度表现为强开放性．

综上，该活动表现为弱综合性、强实践性、强开放性，属于中要求型活动．通常而言，这类活动具有一定难度系数，学生完成活动的耗时并不短，比较适合出现在教科书中专门的活动探究类栏目当中．

3.2.3 高要求型活动

高要求型活动，即在3个特征维度上都具有强表现水平的活动．例如基于《标准（2022年版）》中的活动实例“绘制公园平面地图”[4]所开发的项目式学习活动．

为满足游客的个性化需求，公园常常需要提供不同主题的地图．请以学校附近的某公园为对象，以小组为单位，共同选择一个你们小组感兴趣的主题，如文化古迹、景观、建筑、古树、定向越野打卡点、小吃售卖点等，根据实地测量绘制对应主题的公园平面地图．并请每小组推选出一名公园导游，通过所绘地图，向全班同学介绍公园中对应主题元素的分布情况，最后通过同学的反馈调整你们组的地图设计．

就综合性而言，该活动主要涉及数学、地理、美术3个学科，而受学生选择主题的不同，还可能与其它学科相关联，例如文化古迹对应的历史学科，古树、植物分布对应的生物学科，定向越野对应的体育与健康等学科领域．在具体绘制地图时，需要结合相关学科知识确定地图中的要素，结合实地测量数据进行数学抽象，将真实的公园抽象为图象表示，再结合美术知识进行富有美感的地图绘制．因此，该活动在此维度表现为强综合性．

就实践性而言，该活动需要学生选出感兴趣的主题、对公园进行实际测量、绘制公园地图、作为导游向全班介绍，其中多数活动还需要团队合作完成．尤其对公园的实地测量，可能会用到许多数学知识解决一些不可测问题，这需要学生结合实际情况进行设计并实施测量，具有较高的挑战性．因此，该活动在此维度表现为强实践性．

就开放性而言，由于绘制地图的主题是通过小组讨论得到，供学生绘制的公园也由学生根据各地条件进行选择，则活动的问题与条件均为开放的；而学生在实地测量、绘制地图、介绍公园等活动中的行为表现，更是因人而异，体现出活动过程与结果上的开放性．因此，该活动在此维度表现为强开放性．

综上，该活动表现为强综合性、强实践性、强开放性，属于高要求型活动．通常而言，这类活动具有较大的难度系数，学生完成活动的耗时较长，比较适合出现在教科书中专门的跨学科主题学习或项目学习的栏目当中．

4 “综合与实践”活动的呈现要点

开发数学教科书“综合与实践”活动时，除了要把握好3个关键特征，还有一些活动呈现中的要点也需要关注，包括：以“问题”引领活动设置，以“过程”指导活动实施，以“评价”保证活动质量．这些呈现要点既是“综合与实践”活动关键特征融入教科书文本的有效保障，也是教师能够组织好“综合与实践”活动的有力抓手．

4.1 以“问题”引领活动设置

问题是数学的心脏．对于数学教科书“综合与实践”活动的设置，问题也充当着活动心脏这一重要角色，是整个活动的动力源泉．《标准（2022年版）》指出，“综合与实践”活动：要以问题解决为导向……让学生从数学的角度观察与分析、思考与表达、解决与阐释社会生活以及科学技术中遇到的现实问题……提高发现与提出问题、分析与解决问题的能力[4]．从这一要求出发，“综合与实践”活动应通过问题引领学生进行数学地观察、思考与表达，以达成学生的发现、提出、分析、解决问题能力的提升．

从落实“综合与实践”活动关键特征的视角来看，在教科书中设置“问题”引领活动，要注意如下方面．首先，活动应选择真实的综合性问题情境，它们可以来自日常生活，也可以是跨学科的，基于这些真实的综合性情境得到的问题有助发展学生的发现与提出问题能力．其次，问题应具有较强的探究价值，通过问题探究过程的步步深入，将引导学生开展观察、操作、比较、分析、讨论、设计、制作等各类实践性活动．此外，设置开放性问题也很必要，不仅有助满足不同学生的发展需求，还能使整个活动具备多样化的发展路径．

例如，对于“比赛场地规划”活动，首先向学生呈现学校运动会需提前规划比赛场地这一问题情境，完成该活动需要学生掌握一定的体育项目场地知识，以及足够的几何学知识，体现出活动的综合性．其次，通过一系列具体问题（如：某项比赛对应的场地的要求是什么？如何用数学的语言刻画所在学校的真实场地特点？如何基于实际情况合理地设计比赛场地？），引导学生开展查阅资料、调查或测量场地、合作解决问题等实践性活动．最后，建议学生可以根据各自兴趣、能力及所在学校的场地特点，提出并解决问题，这些开放性问题使活动实施充满更多可能，活动结果具备更多未知．

还需强调的是，要使问题引领整个“综合与实践”活动，要处理好问题的适用性，如问题能够激发学生的挑战欲望、问题解决符合学生的能力等．只有保证学生兼备解决问题的意愿与能力，才能够使活动问题真正引领整个活动．

4.2 以“过程”指导活动实施

相比于旧课标，《标准（2022年版）》对以跨学科主题学习为主的“综合与实践”活动赋予了新的内涵，使得“综合与实践”活动成为了教学实施的难点．作为数学课堂教学的重要资源，教科书充当着既是教材、又是学材的重要角色，应具备足够的教学实施指导性．因此，对于“综合与实践”活动，尤其高要求型“综合与实践”活动，教科书有必要呈现出必要的活动过程，以此作为活动实施的文本指导．

优质的教科书“综合与实践”活动过程，应该为学生呈现出清晰的活动过程结构．通常而言，以帮助学生获取某数学知识为目标的主题式学习活动，其活动过程可形象地比喻为蛛网型；而以解决问题为目标的项目式学习，其活动过程大体呈现出线性结构．学生一旦能够清晰地认识整个活动的实施过程，知晓活动每一步的目的和作用，自然也就能做到对活动实施心中有数．在具体编写教科书时，体现明显的活动过程结构，能够起到良好的活动实施辅助作用．例如在美国教科书中，其跨学科学习栏目My Big Ideas Projects中的每个活动，都可以按照“项目引言→重要问题→问题辅助→一般问题→项目说明”的流程进行划分，使得整个活动过程一目了然[17]．又比如上文所讨论的“比赛场地规划”活动，可以明确提出组建活动团队、开展活动（确定活动项目、实地和资料调查、设计规划图纸）、撰写活动报告、交流展示评价等活动过程．

除了在教科书中体现活动的整体过程，对一些关键活动任务步骤的详细说明，也是提升教科书服务于学生的“综合与实践”活动质量的重要体现．例如使用通俗易懂的文字说明，以及为学生提供适宜的活动过程范例，都可以为其较好地完成关键活动步骤搭建脚手架．

4.3 以“评价”保证活动质量

评价是保证教学活动质量的重要手段之一．数学教科书中最常见的学生学习评价工具是各种习题，如计算题、选择题、解答题等，将其用于评价学生是否掌握了对应的数学知识，是否具备对应的数学核心素养．而对于《标准（2022年版）》要求下的“综合与实践”活动，其主要目标在于培养学生应对兼具综合性、实践性、开放性特征的问题的能力，具体表现为数学核心素养、问题意识、跨学科思维、批判性思维、沟通表达能力，等等．因此，仅通过常规数学习题无法考察学生完成“综合与实践”活动的质量，需要在教科书中设置能够有效衡量学生各种能力的多样化评价方式．

利用教科书评价学生完成“综合与实践”活动的质量，既要体现结果性评价，又要注重过程性评价．进行结果性评价，即评价学生最终完成活动要求的情况，例如要求学生画出设计图、找到任务解决方案、建立数学模型并判断其与实际情况是否相符等．进行过程性评价，即评价学生在活动过程各阶段的任务完成情况以及表现，例如学生在合作小组中的工作表现及完成情况、与同伴交流的顺畅性、在活动中的耐挫表现等．在教科书中，结果性评价主要以活动问题呈现，过程性评价可以通过要求学生填写小组合作任务清单、撰写活动感受、分享活动经验等方式实现．

值得注意的是，因为“综合与实践”活动是一项学习活动，而非学业考评活动，所以要将评价的目标更多地指向学生的学习与发展．因此，在教科书“综合与实践”活动中体现评价，应突出以评促建、增值评价等理念，帮助学生正确认识自身在活动中的能力水平及发展提升．

[1] 胡焱，蒋秋．数学教育与STEM（STEAM）教育的融合：机遇与挑战——基于数学教育与STEM（STEAM）教育国际学术研讨会[J]．数学教育学报，2019，28（6）：92–94．

[2] 王科，李业平，肖煜．STEM教育研究发展的现状和趋势：解读美国STEM教育研究项目[J]．数学教育学报，2019，28（3）：53–61．

[3] 中华人民共和国教育部．义务教育课程方案（2022年版）[M]．北京：北京师范大学出版社，2022：11．

[4] 中华人民共和国教育部．义务教育数学课程标准（2022年版）[M]．北京：北京师范大学出版社，2022：5–6，16–17，77–78，115，172–175．

[5] HOWSON G. The development of mathematics textbooks: Historical reflections from a personal perspective [J]. ZDM, 2013, 45 (5): 647–658.

[6] REYS B J, REYS R E, CHAVEZ O. Why mathematics textbooks matter [J]. Educational Leadership, 2004, 61 (5): 61–66.

[7] 石鸥．教科书概论[M]．广州：广东教育出版社，2019：190–193．

[8] 翟志峰，董蓓菲．国内外教科书评价标准的评价维度和价值取向——基于NVivo11.0的编码分析[J]．教育学报，2022，18（1）：74–85．

[9] YAKMAN G, LEE H. Exploring the exemplary steam education in the U.S. as a practical educational framework for Korea [J]. Journal of the Korean Association for Science Education, 2012, 32 (6): 1 072–1 086.

[10] 李志辉，邵晓霞．我国中小学跨学科教学实施之动因、困境及对策探析[J]．现代中小学教育，2020，36（5）：34–39．

[11] 余文森．学科育人价值与学科实践活动：学科课程新标准的两个亮点[J]．全球教育展望，2022，51（4）：14–15．

[12] SMALL M. Good question: Great ways to differentiate mathematics instruction in the standards-based classroom [M]. New York: Teachers College Press, 2017: 6.

[13] 张侨平．数学开放性问题和平行任务的设计：处理数学学习差异的一种途径[J]．课程·教材·教法，2021，41（1）：105–109，137．

[14] 朱德全，李平，陈亮．基于开放性问题解决的实践性思维数学教学设计[J]．中国教育学刊，2005（4）：46–49．

[15] 李健，李海东．情境在现实问题解决中的作用——基于5套人教版初中数学教科书的纵向比较[J]．数学教育学报，2021，30（4）：30–34，40．

[16] 徐斌艳．如何理解数学教育中问题的开放性——访德国柏林洪堡大学舒尔茨教授[J]．全球教育展望，2001，30（8）：1–3，18．

[17] 李健，李海东．数学课程跨学科主题学习项目的设置与启示——基于美国教科书的分析[J]．上海教育科研，2022（8）：17–23．

Synthesis and Practice Activities of Mathematics Textbook under the Idea of New Curriculum Standard: Key Features, Basic Types, and Presentation Points

LI Hai-dong, LI Jian

(Curriculum and Teaching Materials Research Institute, People’s Education Press, Beijing 100081, China)

In order to meet the cultivation needs of innovative talents, thehas given a new connotation to the synthesis and practice activity. The compilation of synthesis and practice activity in mathematics textbooks will provide an important guarantee for the implementation of the new curriculum standard. The three key features of synthesis and practice activity in mathematics textbooks are synthesis, practice and openness. Based on the key features, a three-dimensional characteristic model of synthesis and practice activity is constructed, and the basic activity types of low, middle and high school students with different requirements are integrated according to the actual situation of textbook compilation. When developing the synthesis and practice activity of mathematics textbook, we should not only grasp the key features, but also pay attention to some key points of presentation, including “problem” to lead the activity setting, “process” to guide the activity implementation, and “evaluation” to ensure the activity quality.

curriculum standard; mathematics textbooks; synthesis and practice; interdisciplinary

G40–03

A

1004–9894（2022）05–0014–05

李海东，李健．新课标理念下的数学教科书“综合与实践”活动：“关键特征”“基本类型”与“呈现要点”[J]．数学教育学报，2022，31（5）：14-18．

2022–08–10

2019年度教育部人文社会科学研究规划基金项目——高中数学核心素养理论框架的实证及实践研究（19YJA880009）

李海东（1973—），男，河北遵化人，编审，主要从事中学数学课程、教材、教学研究．

[责任编校：周学智、陈汉君]