美英早期代数教科书的代数价值观探析

邵爱娣，刘思璐，汪晓勤

美英早期代数教科书的代数价值观探析

邵爱娣1，刘思璐2，汪晓勤2

（1．上海市延安初级中学，上海 200050；2．华东师范大学 教师教育学院，上海 200062）

选取1800—1959年间出版的155种美英早期代数教科书，考查其前言及正文引言部分有关代数教育价值观的内容．研究发现代数教育价值观可分为学科基础、思维训练、品质培养、实际应用、数学交流、情感信念、学科优势7类．以20年为一个时间段，每个时间段7类价值观都不同程度地出现．从代数运算、公式、方程、图象和问题5个方面分析了代数教育价值观在教科书中的体现．启示今天的中学代数教学与教科书编写要注重代数价值观的实现．

代数；教育价值；语言；思维；应用

1 问题提出

理想的教学要求教师不仅要知道“教什么”“如何教”，还要知道“为何教”[1]，教师只有深刻理解数学的价值，才能知道“为何教”．关于数学的价值，《普通高中数学课程标准（2017年版）》（以下简称《标准》）指出：“数学是自然科学的重要基础，在形成人的理性思维、科学精神和智力发展中发挥着不可替代的作用，它还是表达与交流的语言，其应用渗透在人们日常生活的各个方面．”《标准》还在课程目标中提出“让学生认识数学的科学价值、应用价值、文化价值、审美价值”的要求[2]．调查研究表明[3-4]，学生在初等教育时期，受以功利性和实用性为主的升学考试的影响，随着年段的升高，其数学观各维度的水平逐步下降，高中最低．鉴于此，一些学者大力提倡在数学教学中凸显数学的价值，改变学生消极的数学观[5-7]．

代数是数学的一个分支，在中小学数学教育中占有重要地位．要在代数教学中体现数学的价值，首先需要深入探讨代数学所特有的价值．虽然有许多学者在这方面[8-10]做过研究，但很少见到基于历史视角的文献研究．事实上，对于代数学价值的探讨可以上溯至17世纪，法国数学家笛卡儿称“一切问题均可转化为代数问题，一切代数问题均可转化为方程问题”．19世纪以来，部分西方代数教科书中或多或少都对代数学教育价值作过探讨，对这些代数教科书的价值观进行考查，一方面能帮助今天的教师更深刻、全面地理解代数的教育价值，另一方面也能够为今日代数教学和教科书编写带来一定的启示．对1800—1959年间出版的美英早期代数教科书进行考查，试图回答以下问题：早期代数教科书提出了代数学的哪些教育价值？这些价值在教科书中是如何体现的？对今日中学代数教学和教科书编写有何启示？

2 研究方法

2.1 对象选取

研究者详细阅读Hathi Trust数字图书馆中两百余种出版于1800—1959年间的美国和英国代数教科书的前言和正文引言部分，从中筛选出论及代数学价值的教科书作为研究对象．关于代数价值的表述有以下4类：（1）直接描述代数学的价值；（2）描述数学的价值，因其出现在代数教科书的前言部分，将其归为代数的价值；（3）描述该教科书或教科书的某一部分（如例题）所要达成的教育价值，因其出现在代数教科书的前言部分，将其归为代数学的价值；（4）描述代数学中某一个知识点的价值．

对于同一作者再版的教科书，若书名不一致或书名虽同但内容不一致，则视为不同的教科书，否则视为同一种．最终确定155种，其中112种在前言中论及代数学的价值，25种在正文引言部分论及代数学的价值，18种在前言和正文引言部分同时论及代数学的价值．若以20年为一段，则155种代数教科书的分布情况如图1所示．

图1 155种教科书的时间分布

2.2 分类框架的建立

早在1920年，Kelley在哥伦比亚大学《教师学院院刊》发表了一项关于中学代数价值的调查研究[11]．为了回答“中学代数的价值是什么”这个问题，作者对数学家以及从事各行各业的人们进行了一项调查．研究者对Kelley的调查结果进行分析和归类，据此形成初步的代数价值分类框架．运用该框架对早期代数教科书的代数价值观进行统计时，根据统计情况，反过来又对分类框架进行适当修正，最终形成正式的代数价值分类框架，见表1．

表1 代数学价值的分类框架

2.3 分类统计

确定统计框架后，由两位研究者运用文本分析法对155种教科书的前言及正文引言部分进行研究，提炼出其中关于代数价值观的统计单位，根据分类框架对统计单位进行分类．对于分类有争议的地方，两位研究者进行再讨论，直至全部一致．

统计结果显示，共有81种教科书论及一类价值，47种教科书论及两类价值，19种教科书论及三类价值，4种教科书论及四类价值，两种教科书论及五类价值，两种教科书论及六类价值．七类价值共出现270次，具体分布情况见图2．

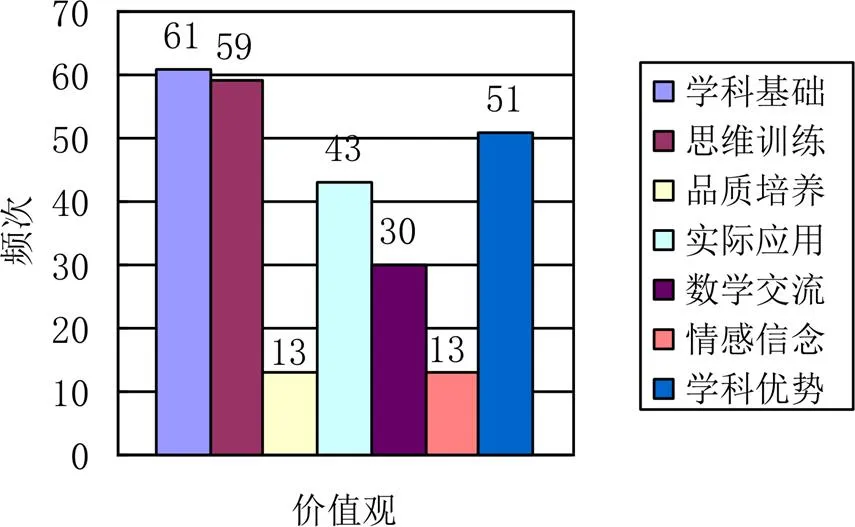
图2 代数教育价值观的分布

3 代数价值观具体分类

3.1 学科基础

共有61种教科书（占39.4%）提及代数作为学科基础的价值，这也是代数价值观中占比最多的一类．数学上，除了算术和初等几何以外，没有什么学科离得开代数学．三角学、解析几何、微积分，没有代数学可谓寸步难行．作为跨学科基础，代数知识是学习物理、化学、工程、商业等其它学科所需的必备知识．表2给出了代表性的具体观点．

3.2 思维训练

共有59种教科书（占38.1%）提到代数的思维训练价值．通过学习代数，学生能够提高智力，增强逻辑推理能力，发展抽象概括能力，并且能够缜密地思考问题等．总之，这里的思维训练是指跟脑力活动相联系的教育价值．表3给出了代表性的具体观点．

3.3 品质培养

共有13种教科书（占8.4%）提到代数在培养学生品质方面的价值．这里的品质指的是学生的行为和作风显示出来的品性、认识等．无论是锻炼坚韧的意志、培养良好的习惯，还是培育探索精神、增加卓识远见，学习代数都带来了很大的帮助．表4给出了代表性的具体观点．

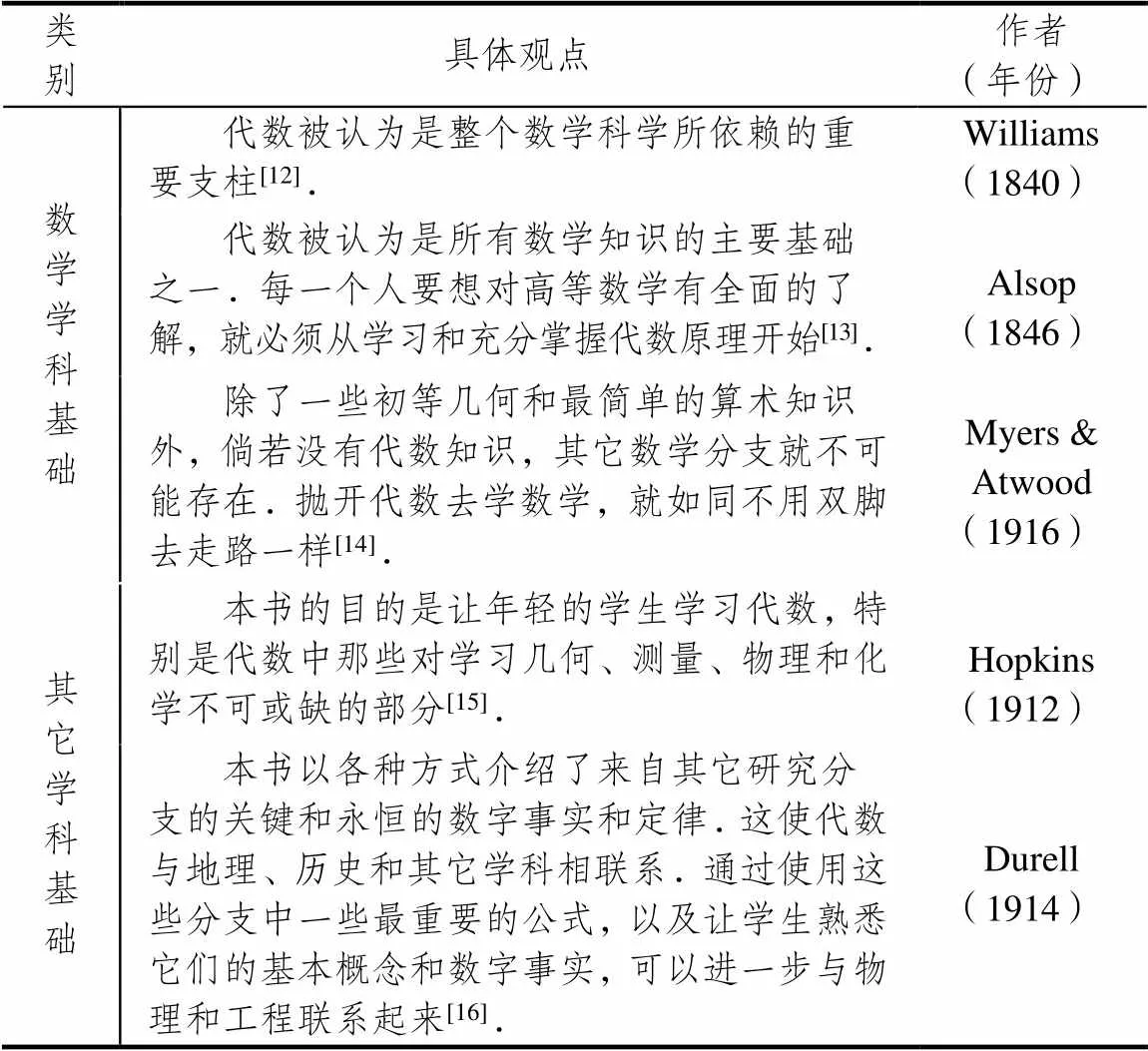
表2 关于学科基础的代表性观点

表3 关于思维训练的代表性观点

表4 关于品质培养的代表性观点

3.4 实际应用

共有43种教科书（占27.7%）提到了代数的实用价值．代数渗透于日常生活的许多方面，是从事多种行业的人员必需掌握的一门学科．表5给出了代表性的具体观点．

3.5 数学交流

共有30种教科书（占19.4%）给出了代数在数学交流上的价值．代数语言是人们精确表达思想的强有力的工具，同时，代数也能锻炼学生的表达能力．表6给出了代表性的具体观点．

表5 关于实际应用的代表性观点

表6 关于数学交流的代表性观点

表7 关于情感信念的代表性观点

3.6 情感信念

共有13种教科书（占8.4%）认为，学习代数有助于促进学生对该学科的情感和信念的一种变化．这里的情感信念指的是学生对于数学学科或数学学习的一种态度的感受和认识．表7给出了代表性的具体观点．

3.7 学科优势

共有51种教科书（占32.9%）指出，与算术相比，代数有其独特的优势．代数是算术的一种延续，它能解决用算术和几何方法难以解决或不可能解决的问题．表8给出了代表性的具体观点．

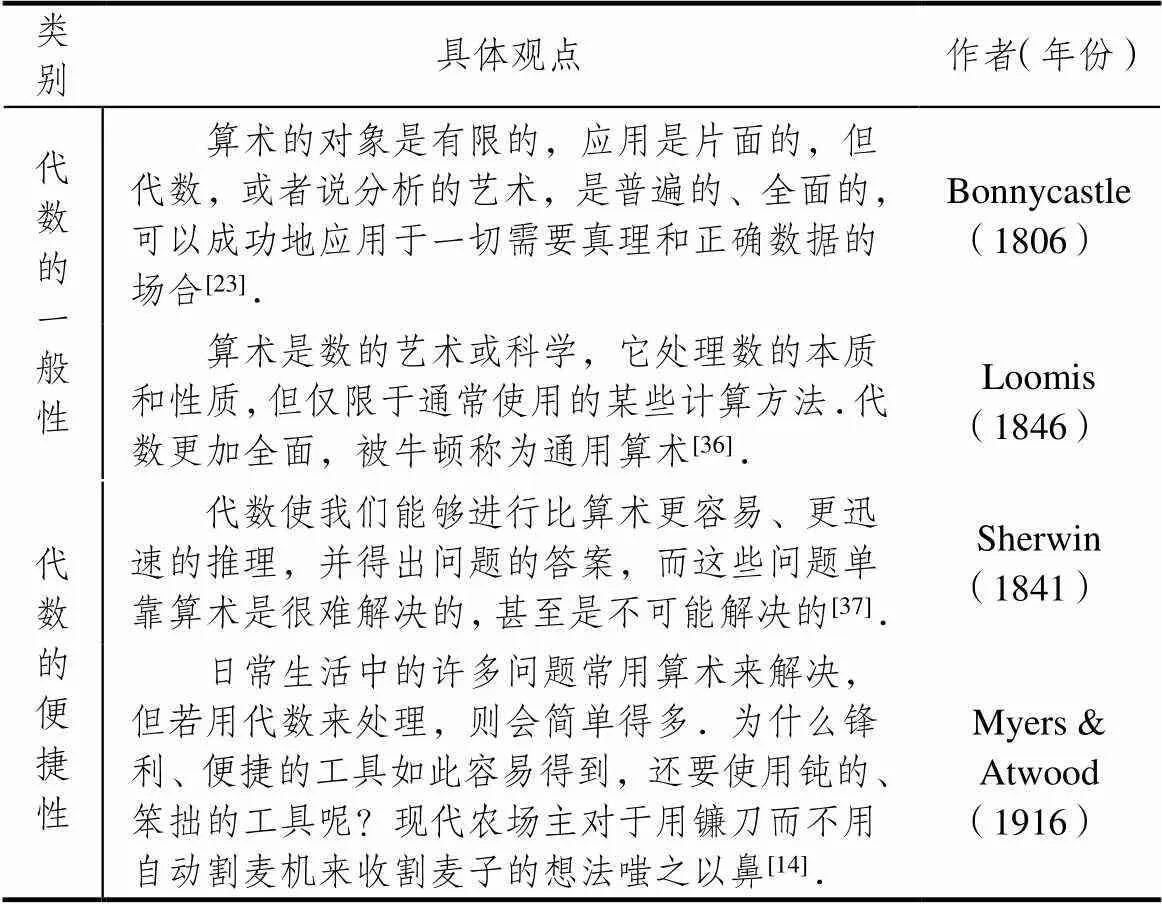
表8 关于学科优势的代表性观点

4 代数价值观的分布

由于每个年段的书本数量有差别，因而对上述7类代数价值观在其年段所占比率进行统计，并绘制图表．图3给出了各类价值分布的变化情况．

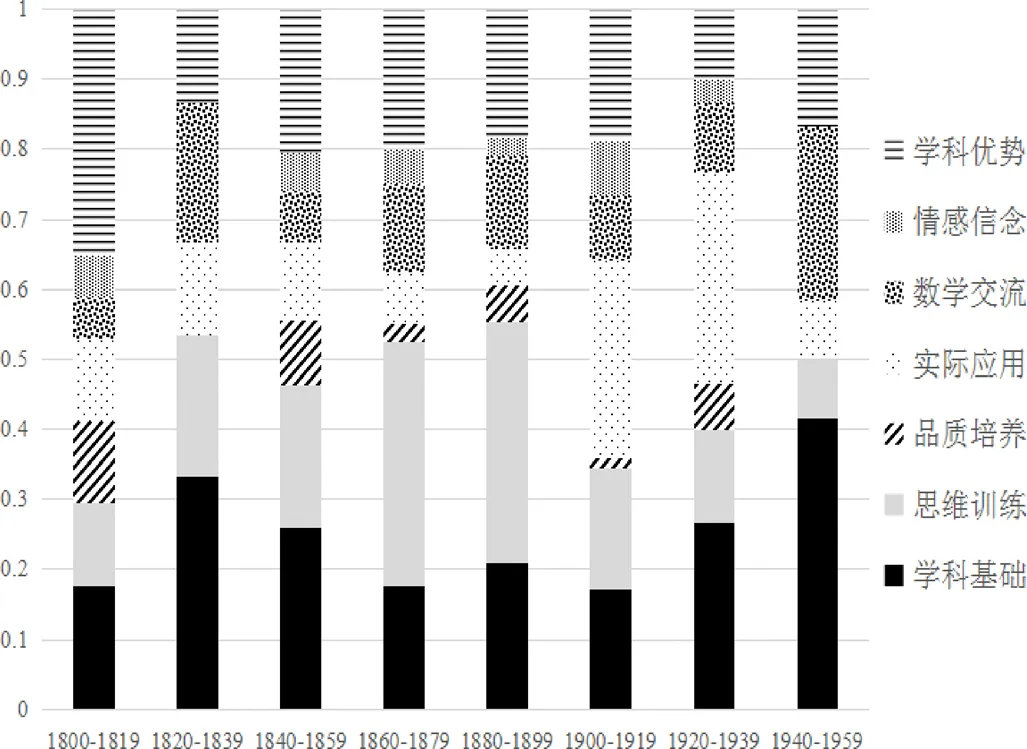
图3 各类价值分布的变化情况

从图3可见，以20年为一个时间段，则160年分成了8个时间段．其中品质培养和情感信念出现在其中的6个时间段，其余5种价值出现在所有时间段．由此，19世纪到20世纪上半叶，代数教科书的编写者对代数的7种教育价值都有所关注．总的来说，早期代数教科书呈现出了代数教育价值的多样性．就单个价值而言，学科基础和思维训练两种价值占比最高．而变化比较明显的是思维训练和实际应用，19世纪末，思维训练占比较高，进入20世纪之后，实际应用占比迅速上升，这与20世纪初西方的数学教育改革运动息息相关．

5 代数价值观在教科书中的体现

在对早期代数教与学的研究中发现，Hotz从加法和减法、乘法和除法、方程和公式、问题、图象5个方面制定了代数测试量表[38]；Durell从口头和书面问题、图象、公式、新颖的例子等方面给出了代数教学的建议[39]；而Thorndike从公式、方程、问题、图象4个方面阐述了学习代数需要具备的能力[40]．因此，早期教科书编写者比较注重学生对于代数运算、公式、方程、图象和问题5个方面的学习．研究者将从这5个方面来分析代数价值观在教科书中的体现．

5.1 代数运算

相比于算术，代数运算代表了更一般化的数字运算，因而早期代数教科书通过代数运算来培养学生的抽象和概括能力．如Lyman等在讲解多项式乘以多项式时类比两位数竖式乘法的方式[41]，如图4，要把32乘以24，可以先把30+2乘以4，然后再乘以20，最后把部分乘积相加．要把2+3乘以3+，先把2+3乘以3，然后再乘以，最后把部分乘积相加．该过程让学生体会从特殊的例子当中抽象出一般的代数乘法的运算过程，从而达到锻炼学生思维的目的．

图4 Lyman多项式乘法运算

此外，Gillet认为反复练习代数运算有助于加强记忆、加快理解，培养精确的习惯[42]．可见，早期代数教科书通过代数运算来训练学生的思维、培养学生良好的品质．

5.2 公式

早期代数教科书给出许多物理、工程、商业等学科中的公式以及运算．Wentworth等写道：“今天任何一种商业活动中，公式都是非常有用的．没有公式的知识、价值和帮助，一个人不可能成为商业领域的真正主人．”[43]可见公式对于商业领域的重要性．Schorling等也在其教材中突出强调公式的结构、意义和使用，认为公式作为简洁的语言、计算的简写规则、问题的通解、表示一个量对另一个量的依赖关系的方法[44]．

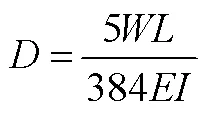
总之，早期代数教科书利用公式来彰显代数的实际应用价值和数学的交流价值．

5.3 方程

方程刻画了现实世界中某些事件所遵循或近似遵循的规则或定律，是初等代数的中心问题．Myers等认为，使用方程的能力是精确思考者的主要装备，代数实质上是方程的科学与艺术[14]．Kent指出，代数的主要目的之一是解决用算术方法难以解决或不可能解决的问题，而方程是获得这些解的手段，事实上方程是这门课的中心思想[46]．Young等通过突出方程在教科书中的地位来体现代数的应用价值[24]．一些教科书专门用整章的篇幅来呈现方程的应用，如Taylor分别用一章的篇幅介绍一元一次方程（含6道例题、57道习题）和一元二次方程（含6道例题、53道习题）的应用[47]．

因此，方程是早期代数教科书训练学生思维能力、凸显代数学科优势以及实际应用价值的重要工具之一．

5.4 图象

通过图象能够直观地表示出两个变量之间的关系．早期教科书运用函数图象或方程曲线，一方面让学生通过观察图象了解事物的变化规律，从而推断出其中隐含的信息；另一方面让学生动手操作，绘制图象并能根据图象回答问题．

Schorling认为，数学关系的图象表示利用了更广泛的感官体验．在其它条件相同的情况下，附带图象的问题容易被更多的学生理解和欣赏[44]．Schultze等认为图解法不仅有很大的实用价值，而且毫无疑问地提供了一种非常好的方法，以防止“学校代数退化为一种机械地应用记忆规则的倾向”[48]．Slaught等列专章介绍图象表示法[49-50]，其中主要涉及函数或方程的图象或图形．Cajori等用图象来表示午后12小时之内的温度变化情况以及1860—1914年之间美国无烟煤价格的变化情况[51]．Hawkes等在其图象表示法一章中称：“商业世界的科学数据和数字统计经常以图象的形式清晰而简洁地表示出来．”[52]

易知，图象的运用可用来训练学生的思维能力，激发学生的学习兴趣，并解释代数在现实世界的广泛应用．

5.5 问题

这里的问题主要指的是文字题，大部分问题通常具有一定的学科背景或实际背景．Lawrence提到：“在代数教学方面的经验证明，只有把这些原理应用到实际问题的解决中，才能使学生熟悉这些原理．因此，教材中包含大量的实际例子和问题．在选择这些例子时，一个突出的目标是选择那些最有可能使学生感兴趣的，同时这些例子的解决方案又将加强学生的分析能力．”[18]有大量的早期代数教科书会用专门的章节来呈现问题．例如Day等通过专门的章节来阐述了代数在几何中的应用[18，53]，如题“给定了平面三角形的三条边，求它的面积；一个人要高出地球表面多高才能看到地球表面的三分之一？”等．Wentworth第十章一共给出了76道练习题，涉及年龄问题、钟表问题、行程问题、工程问题、图形面积问题、动物比赛问题、军事问题、经济问题等[54]，可谓丰富多彩．

Durell等[55]认为代数的其它任何部分都不如语言问题那样发展思想力量和培养对代数精神的欣赏．Seaver等指出教材中精心安排了问题集，其推理可以很容易地在头脑中进行并通过口头表达出来．这种口头使用代数语言被认为是一种非常有效的教学方法[56]．

可见，早期代数教科书在问题选择时关注了代数的学科基础、思维训练、实际应用、数学交流和情感信念等价值．

6 结论与启示

综上，1800—1959年间155种美英早期代数教科书呈现了7类代数教育价值观，即学科基础、思维训练、品质培养、实际应用、数学交流、情感信念和学科优势．在160年间，7类价值并没有呈现出明显的大起大落现象．由此可见，早期代数教科书编写者对于代数学的价值有着比较全面和客观的认识．早期教科书的代数价值观对今日中学代数教学和教科书编写具有一定的启示．

（1）注重代数的思维训练价值．早期教科书中思维训练价值占了很高的比例，说明代数的学习有助于学生的思维能力发展．在实际教学和教科书编写时，要以该价值的实现为目标，从代数运算、方程求解、问题解答等方面出发，促进学生的积极思考与实践，让学生的思维真正得到锻炼．

（2）促进代数与其它学科的融合．代数作为学科基础这一价值普遍受到了早期教科书编写者的关注，一切需要抽象原理的学科都离不开代数知识．在实际教学中要让学生体会到代数这门学科的优势所在，加强与其它学科的交流，如从公式应用、问题设计等方面着手，让学生体会到代数在其它学科发展中的重要性．

（3）重视代数学习对学生的品质以及情感信念的影响．学生一开始从算术思维进入代数思维必定会遇到一定的困难，教师要注意对学生进行适当的引导便于他们能顺利渡过这个时期．鼓励学生遇到困难不要退缩，要努力地战胜困难．在代数运算中培养学生的专注力、耐力，在问题解答中培养学生独立思考、积极进取、勇于探索的精神．让学生真正体验到学习代数的乐趣．

（4）加强学生代数表达的训练．代数语言是一种通用语言，其在训练学生表达的精确性和简洁性方面起到了决定性的作用．教学中重视代数语言的学习、加强代数表达的训练，一方面能够有益于学生逻辑思维的培养，另一方面也便于其它相关学科的学习．

（5）坚持课堂教学与实践相结合．代数的实用价值表明：数学源于生活，又服务于生活．很多学生因为缺乏生活实践，因而对书本上的内容一知半解．代数教学既要挖掘生活素材，又要让学生走出课堂，进入生活．从公式应用、图象辅助、问题设计等方面让学生感知代数的实用价值，消除代数无用的疑虑．这就要求教师从改变课堂教学方法入手，让学生成为课堂的主人，通过自身的体验感知，从而真正理解数学知识．

[1] Young J W A. The teaching of mathematics in the elementary and the secondary school [M]. New York: Longmans, Green & Co., 1907: 11.

[2] 中华人民共和国教育部．普通高中数学课程标准[M]．北京：人民教育出版社，2018：1-8．

[3] 周琰，谭顶良．学生数学观发展状况的调查研究[J]．数学教育学报，2010，19（4）：27-30．

[4] 谢明初．数学教育的人文追求[J]．数学教育学报，2015，24（1）：6-8．

[5] 周立栋．学生数学意识养成教育——数学教育应有的价值取向[J]．上海教育科研，2010（4）：93-94．

[6] 吴维煊．勿让“分数场”遮蔽数学教育的核心价值[J]．教育理论与实践，2011，31（32）：18-20．

[7] 朱立明，马云鹏．基于新课标的学生数学价值感悟研究[J]．数学教育学报，2014，23（5）：33-35，55．

[8] 李忠．数学的意义与数学教育的价值[J]．课程·教材·教法，2012，32（1）：58-62．

[9] 王尚志，胡凤娟．数学教育的育人价值[J]．人民教育，2018（Z2）：40-44．

[10] 刘鹏飞，孟建伟．论数学的人文价值[J]．自然辩证法研究，2019，35（6）：113-117．

[11] Kelley T L. Values in high school algebra & their measurement [J]. Teachers College Record, 1920, 21(3): 246-290.

[12] Williams J D. An elementary treatise on algebra [M]. Boston: Hilliard, Gray, & Co., 1840: iii-v.

[13] Alsop S. An elementary treatise on algebra [M]. Philadelphia: E. C. & J. Biddle, 1846: 3-11.

[14] Myers G W, Atwood G E. Elementary algebra [M]. Chicago: Scott, Foresman & Company, 1916: 1-6.

[15] Hopkins J W, Underwood P H. Elementary algebra [M]. New York: The Macmillan Company, 1912: vii-viii.

[16] Durell F. Durell’s algebra [M]. New York: Charles E. Merrill Company, 1914: 3-4.

[17] Clarke J B. Algebra for the use of high schools, academies and colleges [M]. San Francisco: A. L. Bancroft and Company, 1881: iii-v.

[18] Lawrence C D. Elements of algebra [M]. New York: Alden, Beardsley & Co., 1853: iii-iv.

[19] Loomis E. Elements of algebra [M]. New York: Harper, 1876: iv.

[20] Green R W. Gradiations in algebra [M]. Philadelphia: I. Ashmead, 1839: v-vii.

[21] Gilbert J H, Sullivan E. Practical lessons in algebra [M]. New York: Richardson, Smith & Company, 1903: iii-iv.

[22] Tower D B. Intellectual algebra [M]. New York: Daniel Burgess, 1855: 3-6.

[23] Bonnycastle J. An introduction to algebra [M]. Philadelphia: Joseph Crukshank, 1806: iii-vii.

[24] Young J W A, Jackson L L. A second course in elementary algebra [M]. New York: D. Appleton and Company, 1910: iii-iv.

[25] Skinner E B. College algebra [M]. New York: The Macmillan Company, 1917: v-vi.

[26] Jones G W. A drill-book in algebra [M]. Ithaca: George W. Jones, 1892: iii-iv.

[27] Wentworth G, Smith D E. Vocational algebra [M]. Boston: Ginn and Company, 1911: iii-iv.

[28] Comstock C E. Elementary algebra [M]. Peoria, Ill.: C. E. Comstock, 1907: 5-7.

[29] Rothrock D A, Whitacre M A. First year algebra [M]. New York: C. Scribner’s Sons, 1932: v-vi.

[30] Dupuis N F. The principles of elementary algebra [M]. New York: The Macmillan Company, 1900: iii-v.

[31] Ford W B. A brief course in college algebra [M]. New York: The Macmillan Company, 1922: v-vi.

[32] Olney E. Introduction to algebra [M]. New York: Sheldon, 1874: 3-4.

[33] Greenleaf B. A practical treatise on algebra [M]. Boston: R. S. Davis and Company, 1852: iii-iv.

[34] Docharty G B. The institutes of algebra [M]. New York: Harper & Brothers, 1867: v-vi.

[35] Hull G W. Elements of algebra for beginners [M]. New York: American Book Company, 1904: 3.

[36] Loomis E. A treatise on algebra [M]. New York: Harper & Brothers, 1846: 10.

[37] Sherwin T. An elementary treatise on algebra [M]. Boston: Sanborn, Carter, Bazin, 1841: 1.

[38] Hotz H G. First year algebra scales: Series a [M]. New York: Teachers College, Columbia University, 1920: 26.

[39] Durell F. Suggestions on the teaching of algebra [M]. New York: Charles E. Merrill Company, 1921: 10-13.

[40] THORNDIKE E L, WOODYARD E, WALD E, et al. The psychology of algebra [M]. New York: The Macmillan Company, 1923: 100-120.

[41] Lyman E A, Darnell A. Elementary algebra [M]. New York: American Book Company, 1917: 74.

[42] Gillet J A. Elementary algebra [M]. New York: H. Holt and Company, 1896: iii-v.

[43] Wentworth G, Schlauch W S, Smith D E. Commercial algebra: Book I [M]. Boston: Ginn, 1917: iii-iv.

[44] Schorling R, Clark J R. Modern algebra: Ninth school year [M]. Yonkers-on-Hudson, N.Y.: World Book Company, 1924: iii-viii.

[45] Stone J C, Millis J F. Elementary algebra: First course [M]. Boston: B. H. Sanborn & Company, 1911: 1-18.

[46] Kent F C. A first course in algebra [M]. New York: Longmans, Green, and Co., 1913: iii-iv.

[47] Taylor J M. Elements of algebra [M]. Boston: Allyn and Bacon, 1900: 99-106, 291-299.

[48] Schultze A, Breckenridge W E. Elementary and intermediate algebra [M]. New York: The Macmillan Company, 1925: v-vi.

[49] Slaught H E, Lennes N J. Elementary algebra [M]. Boston: Allyn and Bacon, 1915: 230-239.

[50] Rietz H L, Taylor E H, Orathorne A R. School algebra: First course [M]. New York: H. Holt and Company, 1915: 180-191.

[51] Cajori F, Odell L R. Elementary algebra [M]. New York: The Macmillan Company, 1915: 16, 63-76.

[52] Hawkes H E, Touton F C, Luby W A. First course in algebra [M]. Boston: Ginn and Company, 1917: 200-210.

[53] Day J, Thomson J B. Elements of algebra [M]. New Haven: Durrie & Peck, 1844: 232-245.

[54] Wentworth G A. Elements of algebra [M]. Boston: Ginn & Heath, 1881: 137-150.

[55] Durell F, Arnold E E. A second book in algebra [M]. New York: C. E. Merrill, 1920: iii-iv.

[56] Seaver E P, Walton G A. The Franklin elementary algebra [M]. Philadelphia: J. H. Butler, 1882: iii-vi.

Educational Values of Algebra in U.S. and English Textbooks Published between 1800 and 1959

SHAO Ai-di1, LIU Si-lu2, WANG Xiao-qin2

(1. Shanghai Yan’an Middle School, Shanghai 200050, China;2. College of Teacher Education, East China Normal University, Shanghai 200062, China)

155 kinds of early American and English algebra textbooks published between 1800 and 1959 were selected to examine the content of the prefaces and introductions on the values of algebra education. It was found that the values of algebra education could be divided into seven categories: foundation of discipline, thinking training, character cultivating, practical application, mathematical communication, emotions and beliefs, and advantages of discipline. Taking 20 years as a time period, the seven types of values appeared in different degrees in each time period. This paper analyzes the reflection of values of algebra education in textbooks from five aspects: algebraic operation, formulas, equations, graphs, and problems. It is suggested that today’s middle school algebra teaching and textbook compilation should pay attention to the realization of algebra values.

algebra; educational value; language; thinking; application

G633.62

A

1004–9894（2022）05–0076–06

邵爱娣，刘思璐，汪晓勤．美英早期代数教科书的代数价值观探析[J]．数学教育学报，2022，31（5）：76-81．

2022–07–11

上海高校“立德树人”人文社会科学重点研究基地之数学教育教学研究基地研究项目——数学课程与教学中落实立德树人根本任务的研究（A8）

邵爱娣（1990—），女，江苏盐城人，硕士，主要从事数学史与数学教育研究．

[责任编校：陈隽、陈汉君]