俄罗斯中学生数学奥林匹克试题中的数学文化

吕孙忠，雷沛瑶，吴尉迟，熊 斌

俄罗斯中学生数学奥林匹克试题中的数学文化

吕孙忠1，2，雷沛瑶1，吴尉迟1，2，熊 斌1，2

（1．华东师范大学 数学科学学院，上海 200241；2．上海市核心数学与实践重点实验室，上海 200241）

俄罗斯在数学竞赛方面有着诸多经验值得中国学习，其命制的竞赛试题也有着人文特色．研究主要对俄罗斯中学生数学奥林匹克决赛试题中的数学文化进行了研究，统计并分析了其中的数学文化类题目在年份变化、内容分布、知识领域分布和不同年级分布间的特点，从中得到了有关数学竞赛命题以及数学资优生培养的相关启示：以知识源流为切点，架初等高等数学桥梁；思各知识领域特色，精心编排展文化之魅；展现数学内在之美，培养资优生臻美能力；融合文化多元特性，提升资优生国际视野．

俄罗斯；数学竞赛；数学文化

1 问题提出

为了选拔一批具有学科特长、创新潜质并有志于服务国家重大战略需求的青少年，教育部于2018年出台了《关于实施基础学科拔尖学生培养计划2.0的意见》，接着又在2020年发布了《关于在部分高校开展基础学科招生改革试点工作的意见》（也称“强基计划”），并联合中国科协颁布了《2021年“英才计划”工作实施方案》，这意味着中国已将拔尖人才的培养提升到了国家重大战略部署的高度[1]．作为基础学科的数学，在科技发展和国家竞争中举足轻重．由于数学学科的特殊性和儿童心智发展的特点，培养数学英才应该把握学生智力发展的关键期，中国在对数学英才的早期识别和培育上也做了较多工作[2]．其中，开展数学竞赛活动可以在基础教育阶段选拔并培养早期的数学英才，它可以培养学生的兴趣、毅力、眼界和品味[3]，并为高等学府选拔科学研究人才．同时，数学竞赛也是数学教育研究的一个重要领域，包括对选手和对比赛试题的研究[4]．对试题的研究通常集中在对试题的编制和难度分析、比较等领域[5-6]，对选手的研究主要包括对参赛选手后续发展的追踪调查[7-9]．这些研究都表明，奥数的学习经历有利于拔尖人才的成长，对其终身发展是有益的，在英才教育中既应当重视数学奥林匹克活动，也应当关注竞赛试题的命制．

数学竞赛活动作为一种教育活动，不仅要选拔并培养数学英才，而且要促进学生人性的完善[10]．《普通高中数学课程标准（2017年版）》（以下简称《标准》）中指出数学教育的基本理念是：“人人都能获得良好的数学教育，不同的人在数学上得到不同的发展．”[11]为数学资优生提供更高水平的学习材料，是社会主义教育的题中应有之义[12]．对数学资优生而言，数学试题除了承担思维训练的任务，还应具有人文素养的导向，注重数学的价值引领，体现数学的科学价值、应用价值、文化价值和审美价值[11]．数学竞赛活动中有不少低年级学生参加，如何让超常学生在发展数学能力的同时保持对数学的兴趣，是开展数学竞赛活动应考虑的[13]．众多研究表明，数学文化可以提高学生的数学学习兴趣[14]．因此，在数学竞赛试题中融入数学文化，既可以体现数学的人文价值，又可以保持资优生的数学学习兴趣，是值得关注的一种命题视角．

国内视域中，无论是已有的数学竞赛试题、教材，还是有关数学竞赛的研究，对数学竞赛试题中的数学文化关注都较少，如何对资优生进行数学文化价值的引领、保持他们对数学学习的兴趣还值得进一步思考．国际领域中，数学奥林匹克具有悠久的历史传统，它在发现和培养数学人才上发挥着重要作用．其中，不乏菲尔兹奖获得者的俄罗斯[15-16]在数学竞赛试题的人文导向上有着丰富的经验．俄罗斯对数学人才的培养极富人文精神，数学奥林匹克试图具有较高的人文情怀，其国家统一考试的数学试题也更注重与实际生活的联系[17]，数学奥林匹克试题不仅数量多，而且质量高[18]，还有不少奥林匹克式的开放性问题[19]，具有丰富的数学文化背景，为中国数学竞赛试题的编制提供了一个值得参考的文化视角．在此背景下，研究提出以下研究问题：俄罗斯中学生数学奥林匹克试题中数学文化类题目在年份变化、内容分布、知识领域分布和不同年级的分布间有何特点？

2 研究设计

2.1 数据来源

全俄中学生数学奥林匹克是受俄罗斯联邦教育部指导的全国性数学竞赛活动，每学年举办一届．从苏联解体后到2008年，每届全俄中学生奥林匹克竞赛进行5轮比赛；自2009年开始，原来的校级竞赛不再作为首轮的竞赛，比赛被缩减为4轮，分别是：市级竞赛、省级竞赛、联邦区域赛和全俄决赛，其中市级竞赛和省级竞赛在第一学期进行，联邦区域赛和全俄决赛在第二学期进行．全俄决赛通常在每年的4月中旬举行，时间并不固定，它是俄罗斯最高层次、最高水平的数学竞赛，功能和水平与中国的中学数学奥林匹克相当，考试分两天进行，要求每天在5个小时内完成4道题目．全俄决赛中设置了九年级、十年级和十一年级，与中国高中的3个年级对应，当年的全俄决赛的优胜者有机会代表俄罗斯参加国际数学奥林匹克竞赛[20]．

研究的具体对象是1993—2019年俄罗斯数学奥林匹克决赛（以下简称全俄决赛）的九年级、十年级和十一年级3个年级的题目，每个年级有8道题目，总计648道题目（由于疫情原因，2020年的比赛没有举行），具体的题目来自苏淳翻译的两本书[18，20]．

2.2 分析框架

2.2.1 数学文化类题目的数量变化趋势

对1993—2019年全俄决赛试题的数学文化进行统计，将每一年3个年级的数学文化类题目总量作为该年的数学文化类题目数量，统计全俄决赛中数学文化类题目数量随年份的变化趋势．

2.2.2 数学文化类题目的内容分布

不同学者对数学文化的定义有不同的理解，研究主要采用《标准》中对数学文化的定义，即“数学文化指数学的思想、精神、语言、方法、观点，以及它们的形成和发展；还包括数学在人类生活、科学技术、社会发展中的贡献和意义，以及与数学相关的人文活动”[11]．根据汪晓勤依据西方学者所总结的数学史的教育价值以及课程标准中要求的数学的4类价值，研究将数学文化内涵划分为知识源流、学科联系、社会角色、审美娱乐和多元文化5个类别[21]，并根据俄罗斯中学生数学竞赛题的特点，结合PISA测试对数学问题情境的分类[22]，将“社会角色”细分，得到了数学竞赛试题中数学文化元素的分类框架，具体见表1．

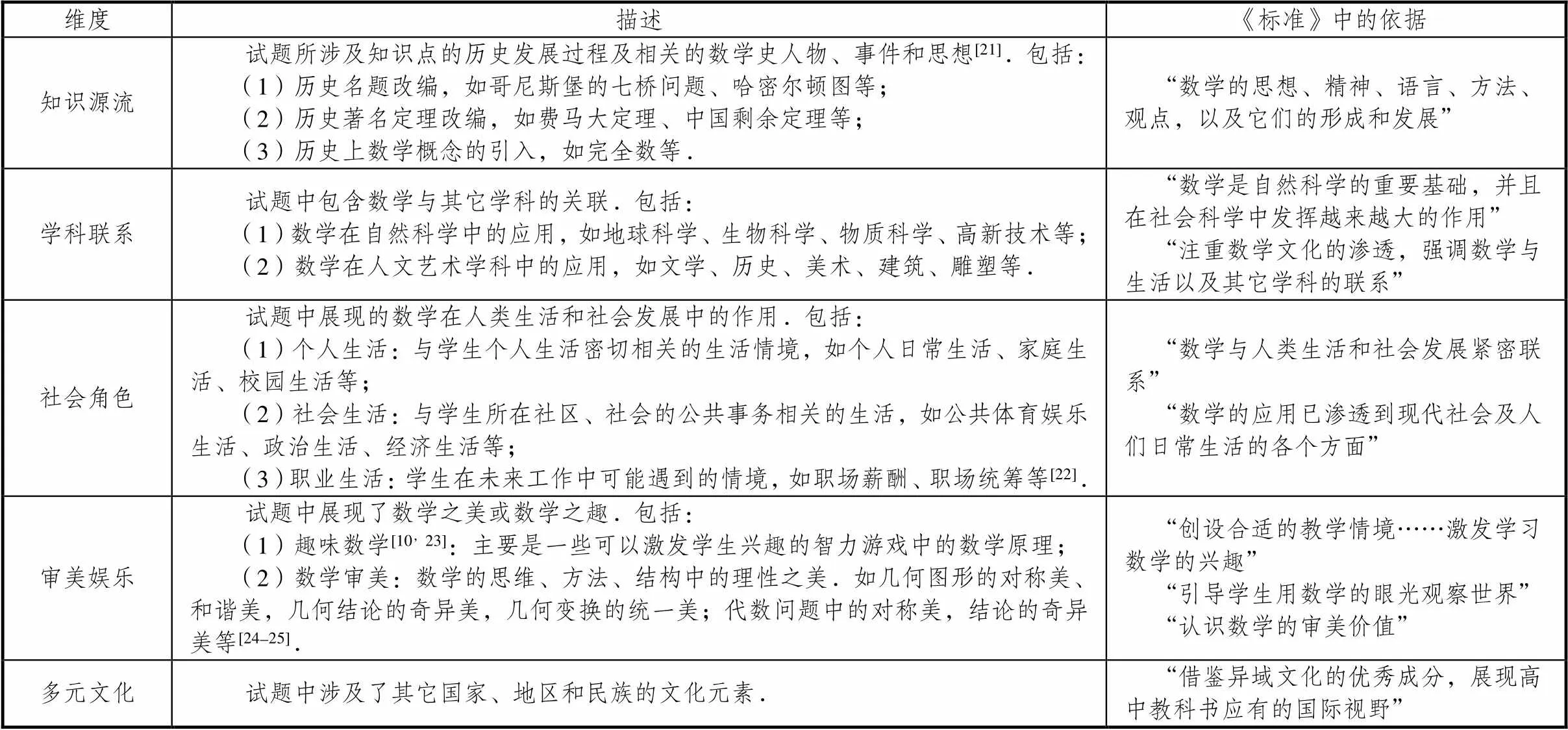
表1 数学竞赛试题中数学文化元素的分类框架

具体地，含有数学文化元素的试题举例如下．

例1 【知识源流】（1999年，十年级）在某个由12个人组成的群体中，任何9个人中都可以找出5个人相互认识．证明：从该群体中可以找到6个人相互认识[18]．

此题和Ramsey原理有一定的关联，Ramsey理论广泛见于科研，又频繁地出现在数学竞赛中，Ramsey理论往往以“人与人之间相互认识或者不认识”的关系出现在科普书上[26]．此题多了一个“可以找出5个人相互认识”的条件，是一道典型的根据历史定理改编的试题，因此将它归类为知识源流．对这类历史上著名命题、定理和名题的巧妙改编，可以让学生感受来自大数学家的思想方法之美，体会数学史上独特的理性光辉．

例2 【审美娱乐】（2015年，十一年级）不死的跳蚤自原点出发，沿着数轴上的整点跳跃．它第1步跃过的距离为3，然后是5，再然后是9，如此一直下去，在第步跃过的距离是2+1．至于第一步是往左跳还是往右跳，全凭跳蚤自己选择．试问：跳蚤是否能跳遍每一个整数点（允许多次到达某点）[20]？

此题以跳蚤为主角创造了一个虚拟的故事场景，数轴上的跳蚤不断跳跃，就像数轴上的点不断移动，由此产生了相关的趣味数学问题．此类试题将数学问题藏身于有趣的故事情节中，将单调的数学语言用风趣的生活语言代替，新颖有趣，可有效地提升学生的数学学习兴趣．

2.2.3 数学文化类题目的知识领域分布

研究根据俄罗斯中学生数学竞赛题目所考察的知识点，将题目的知识领域编码为代数、数论、几何以及组合共4个知识领域，如表2所示．再分别统计数学文化类题目出现在不同知识领域的数量．编码中涉及到多个知识点的试题，研究会将该试题归类到知识点比例较高的领域中去．

表2 知识领域分类框架

2.2.4 数学文化类题目在各个年级上的分布

研究将每一年全俄决赛试题中的数学文化类题目分别统计，由于各个年级的考试同时进行，部分题目会重复出现，针对这一类题目，研究将它们独立编码．例如2017年九年级的第8题和2017年十年级的第7题是同一道题，研究会将它们在九年级和十年级中各记一次．

2.3 编码过程

研究共经历了3轮编码，分为预编码、初编码和二轮编码．在确定理论框架后，进入了预编码阶段．研究人员在进行预编码后，与数学教育专业数学竞赛方向的1名教授、3名博士研究生和数学史方向的1名博士研究生讨论并确定了具体的编码方案，随后开始进行初编码．在初编码阶段，先由1名研究人员独立进行编码，然后随机抽取20%的题目，也就是6年的原始试题（144道），让两名博士研究生分别对数学文化类别和知识领域进行编码，并统计编码一致度．得到关于数学文化的编码一致度为94.44%，关于知识领域的编码一致度为95.83%．由于编码一致度较高，研究人员与两名博士研究生进行讨论、达到统一的编码标准后，展开了二轮编码．二轮编码由研究人员独立将试题进行二次编码，最终得到研究的数据．

3 研究结果

3.1 数学文化类题目的数量变化趋势

将1993年到2019年间全俄决赛中3个年级数学文化类题目的总量分别统计，得到折线图1．

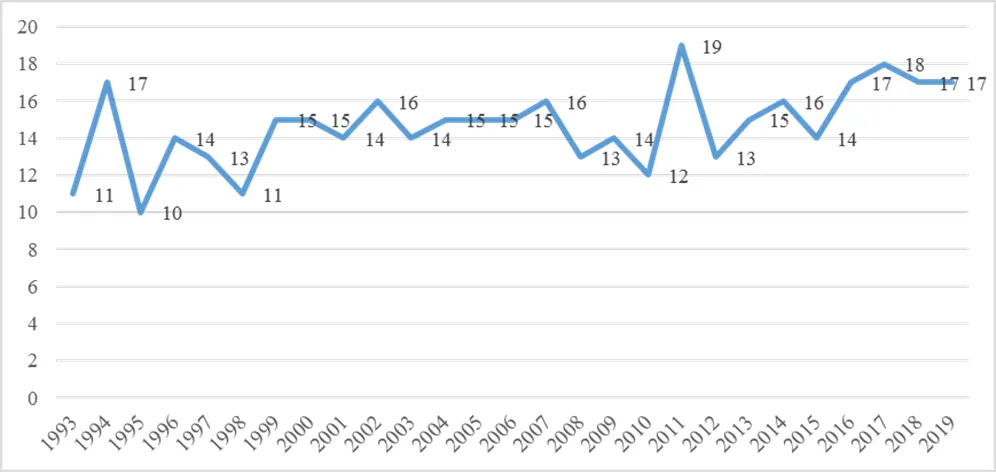
图1 数学文化类题目数量变化折线图

容易看出，全俄决赛开展的这27年间，其数学文化类题目所占的权重每年大致相似．在每年3个年级总题目为24题的情况下，其数学文化类题目多在10～20之间波动，大致占比41.7%～83.3%．除了93年（11题）、95年（10题）和98年（11题）外，其余年份的数学文化类题目都超过了50%，这说明俄罗斯一直就十分重视在竞赛题中传递数学文化．其试题大半具有数学文化背景，有的是有趣的数学游戏情境，有的是自然科学情境，有的是历史名题改编，有的是题目设计者匠心独运地通过试题展示数学美，体现数学的审美价值等．

3.2 数学文化类题目的内容分布

将全俄决赛试题的数学文化类试题按数学文化的类别（知识源流、学科联系、社会角色、审美娱乐和多元文化）分别统计，得到表3和图2．

从表3和图2知，全俄决赛试题中的数学文化试题对各个类别的数学文化均有涉及．具体看来，数学文化类试题大量集中在审美娱乐这一类别，占比71.2%，相比其它4个类别具有绝对的数量优势．其中，数学审美类题目有161道，趣味数学类题目有121道．数学审美类题目主要是通过题目展现一些优美的几何图形和代数结构，让学生感受数学的简洁美、对称美、奇异美等，感受数学在永恒与运动间的不同魅力；趣味数学则是将数学试题进行改编，赋予单调的数学题一些有趣的故事情节，或是将数学问题蕴涵在数学游戏中，如方格染色方案的设计、策略游戏中取胜方案的咨询，或是无限大棋盘上棋子的落定、数学王国中卢布的使用等，让学生在解题的过程中感受数学文化的乐趣．占比第二多的社会角色类问题，则是将数学竞赛与现实生活进行联系，将数学试题放置于现实生活中个人的、职业的、社会的情境中，让学生感受数学学科所发挥的社会角色价值，如与个人家庭生活有关的家族相册、与个人校园生活有关的同学交流、与社会生活相关的体育竞技活动以及与学生未来职业生活相关的程序员写程序等问题，这些问题大多贴近生活，让学生可以直观地体会数学在生活中的作用．

表3 数学文化的内容分布统计

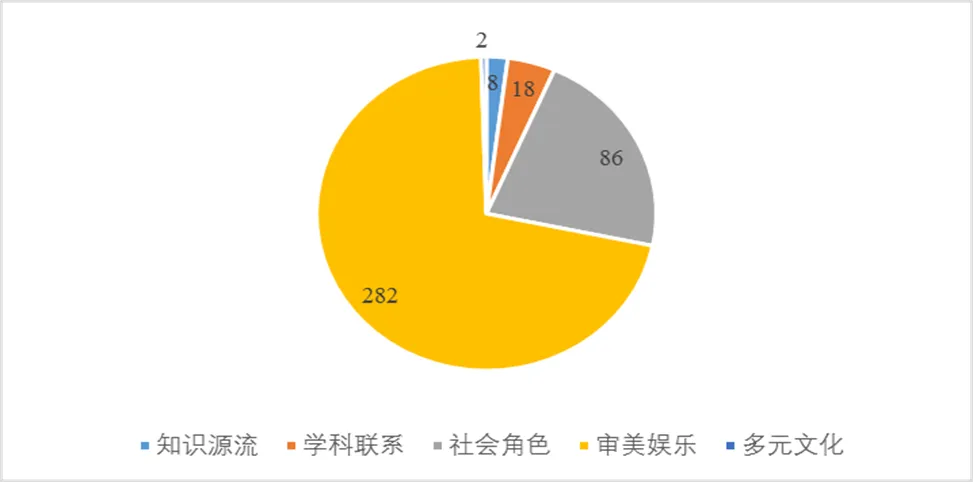
图2 数学文化类题目内容分布饼状图

学科联系有少量的题目（18道），主要集中在与物理学、航空航天学等学科的联系，如通过数学方法计算速度、质量，通过数学方法设计航空路线等，这些题目搭建了沟通数学与其它学科的桥梁，让学生体会数学广泛的应用性．内容分布最少的是知识源流和多元文化两个维度．知识源流只有8道题，主要是将数学史上的历史名题、著名定理等进行改编，如将费马大定理改编为结构类似，但可以用初等简单方法解决的不定方程，用哈密尔顿图改编的图论路线问题，将历史上“完全数”概念引入的数论题等，这些改编的资料都可以作为初等数学联结高等数学的桥梁，它们可以呼唤起学生内心对数学的热爱，让他们成为逐梦的数学人．而多元文化仅有2道题，均来自古希腊的神话传说，出题者别具一格地将古希腊的神话传说编成数学问题，让学生在解题的过程中了解多元文化，既增加了数学题目的趣味，又丰富了学生对世界多元性的了解．

3.3 数学文化类题目的知识领域分布

分别统计数学文化类题目在组合、几何、数论和代数共4个知识领域出现的频数，得到各知识领域出现数学文化类题目的数量．其中，组合共有42题，几何共有131题，数论有42道题，代数有181道题．考虑到试题中各个知识领域题目的数量本就不相同，因此将每个知识领域的数学文化类题目的数量除以该领域题目的总量，得到数学文化类题目在4个知识领域的百分比，见图3．

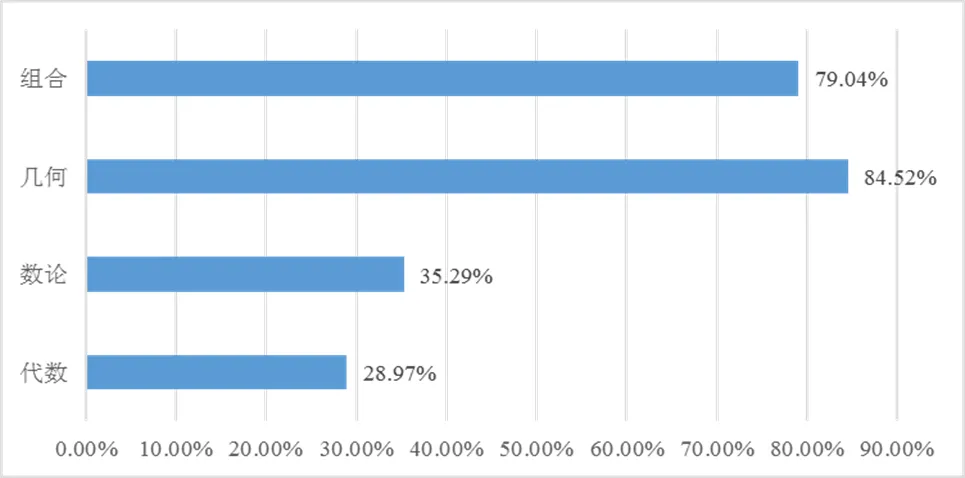
图3 数学文化类题目知识领域分布条形图

由图3可知，数学文化类题目出现最频繁的是几何领域和组合领域，占比均在8成左右．其中，几何试题大部分属于平面几何，也有少量属于立体几何，这个领域数学文化类题目的占比最高，其高达84.52%的试题具有数学文化背景，但是文化背景的类型较为单一，全部来自数学审美．这些数学美有的是图形上的对称、简洁美、奇异美，如对称的直线、简洁的蝴蝶定理、角度的巧合性相等、点的巧合性共圆等；有的是几何变换中的统一美，如位置在改变的某条直线通过某个定点、变换的三角形保持面积不变、旋转位似变化下保持的不变性等．历史上很多优美的平面几何结论就是在很多人不停地探索中发现的，这些数学美可以激发学生对几何结论的自主探索，提升学生对几何位置关系的洞察能力和几何图形的审美能力．数学文化类题目占比第二高的是组合领域，其题目中的数学文化背景比重也达到了79.04%．取材广泛，立意新颖的俄罗斯组合题，需要认真探索、深入思考才能找到试题的答案，是典型性的“动脑题”[18]．组合类题目的文化背景较几何领域的题目更丰富，有的是设计染色的方案、天平称重的方案和分割方格纸图形，有的是游戏策略的输赢，这些问题大多都十分有趣，贴近生活．同时，组合试题结合了其本身就蕴含的丰富的数学方法，如算两次、极端原理、反证法、抽屉原理等，将巧妙的数学思想与丰富多彩的数学文化碰撞，产生了无与伦比的火花，这些试题设计精巧却未令人感到丝毫刻意雕琢之感．另外，有的题目可能还是科研中的副产品，通过解决这些试题，学生也许能在不知不觉中涉足到数学的前沿领域．

数论和代数领域中数学文化类题目占比虽然相对较少，但仍然有3成左右．它们中的数学文化却更多元，都包含了知识源流、学科联系、数学审美和社会角色这4个类别，而代数部分还包括了多元文化．从具体内容的角度来说，它们在学科联系和社会角色上的数学文化类似于组合部分的，但在知识源流和数学审美上有所不同．从数学审美的角度看，俄罗斯竞赛中的数论和代数试题也渗透着代数美学，如在数论试题中定义的“好数”“几乎平方数”“阶好数”等，这些概念映射着特殊的代数结构，在代数试题中，不少全对称或者轮换对称的不等式也闪耀着数学的美学光辉，而这些都是在组合和几何试题中看不到的．

具体地，将4个知识领域在5个数学文化类别中的分布进行统计，得到表4．

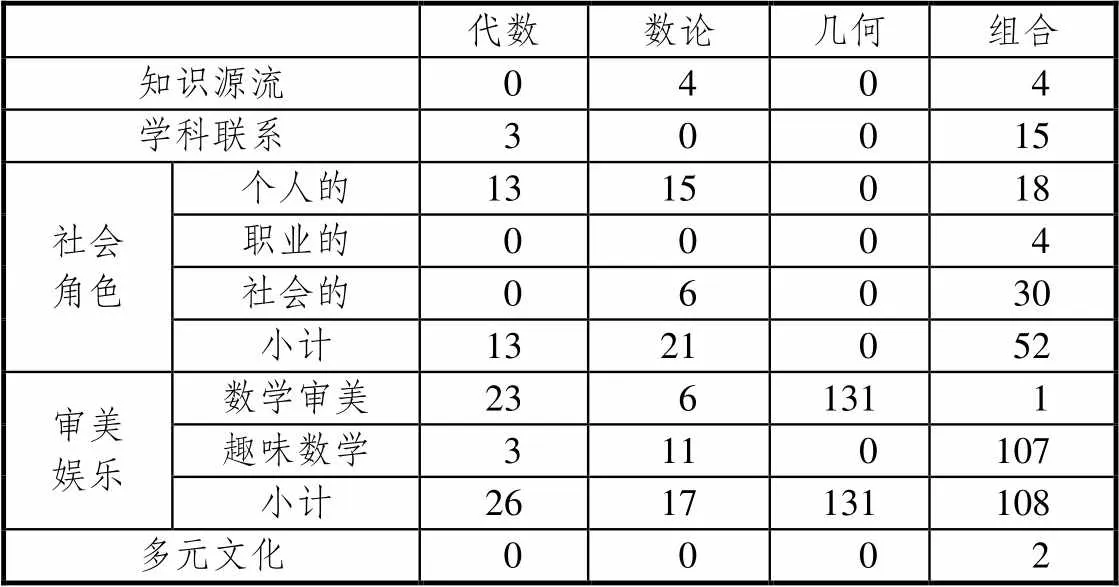
表4 数学文化在各知识领域的内容分布统计

由表4可知，各个知识领域的题目在数学文化各个类别上的分布十分不均衡，利用统计软件SPSS20.0进行Fisher精确检验，得出它们在分布上具有极其显著的差异（<0.01）．具体看来，组合领域题目所蕴含数学文化的种类最多，涵盖了5个类别的数学文化，几何领域所体现的数学文化最单一，仅体现在数学审美上，其余的组合和数论领域也都只涵盖了4个类别的数学文化．

3.4 数学文化类题目在各个年级上的分布

将试题中九年级、十年级和十一年级的题目分别统计，得到：九年级共148道，十年级共130道，十一年级共118道数学文化类题目．对不同年级题目在5个数学文化类别上的具体分布进行了统计，得到了图4．

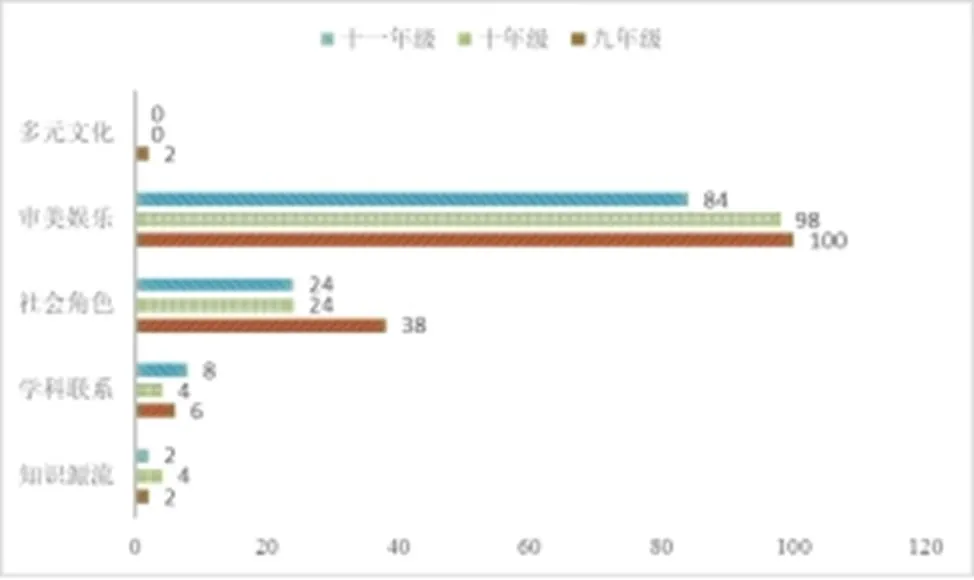
图4 各个年级数学文化类题目分布条形图

3个年级数学文化类题目的总数逐渐减少，九年级最多，十一年级最少．这可能与设计者认为高年级学生的抽象能力更强有关．从图4中可知，尽管总数不尽相同，但各个年级的数学文化类题目在5个数学文化类别上的分布却大致相似，亦无统计学意义上的显著差异（Fisher精确检验=0.450）．3个年级试题中的数学文化最多出现在审美娱乐这一领域，包括一些体现数学审美的题目和蕴含趣味数学游戏的情境．其次是体现社会角色，重点展现数学与个人生活和社会生活的联系．而学科联系、知识源流和多元文化都特别少，尤其是多元文化，试题的里的多元文化仅在九年级出现了两次．

4 结论与启示

研究对全俄决赛试题中的数学文化进行了统计分析，针对研究问题，得到了以下研究结论．

（1）全俄决赛试题中数学文化类题目的占比较大，其从1993—2019年的27年间，数学文化类题目所占的权重大致相似且数量大多超过了总题数的一半；（2）在内容分布上，数学文化类题目分布十分不均衡，主要集中在审美娱乐上，多元文化涉及最少；（3）各个知识领域中数学文化类题目的权重也十分不均衡，几何与组合具有最多的数学文化类题目，且各个知识领域在5个数学文化类别上的分布具有极其显著的差异；（4）3个年级的数学文化类题目数量随着年级的增长依次减少，但在5个数学文化类别上的分布具有相同的趋势．

基于以上研究结论，结合俄罗斯数学竞赛的特点，得到有关数学竞赛命题以及数学资优生培养的以下启示．

4.1 以知识源流为切点 架初等高等数学桥梁

全俄决赛试题中有一些试题直接改编于高等数学知识，如数论里的费马大定理、图论中的拉姆塞数[26]等，这些试题都具有较深的知识源流，蕴含内隐的数学文化．这些竞赛题也可以看作是沟通初等数学和高等数学的桥梁[27]．这也是俄罗斯数学竞赛题的鲜明特色，就连俄罗斯著名数学家柯尔莫哥洛夫也曾在1960年打趣道：“也许，找到证明费马大定理的一种方法是将它作为一道莫斯科数学奥林匹克试题．”[28]数学家们可以将数学研究中部分巧妙的想法，转化为初等数学语言，然后用美丽的故事将它们包装成一道道崭新的数学奥林匹克试题[27]．所以数学奥林匹克试题也值得专业的数学研究人员去探索，因为这些试题可能产生新的研究问题和方向，同时专业的数学研究人员也可以对那部分可以用来作为数学奥林匹克试题资源的高等数学内容保持关注[28]．俄罗斯的数学竞赛还得到了许多数学家们的支持，让学生有更多的机会去接触更前沿的数学[19]；而欧美国家的许多知名高中也开展了大学数学预科课程，这些预修课程和数学奥林匹克教育可以相辅相成．因此，可以邀请更多的数学家来参加数学竞赛的命题、竞赛教辅书的编写和中学数学竞赛课程的教学，从知识源流的角度来编制材料，赋予试题更多的数学文化，引导数学资优生更好地从初等数学学习过渡到高等数学的学习和研究中去．

4.2 思各知识领域特色 精心编排展文化之魅

从数学文化内容在各个知识领域分布的角度来看，全俄决赛试题中代数、数论、几何和组合所蕴含的数学文化类别存在明显的差异．这些特点也为数学文化融入数学竞赛的命题提供了新的思考，在试题编制中应该考虑各个知识领域的特点，为各知识领域的试题融入适合它们知识特点的数学文化，比如几何题可以从数学审美的角度考虑，而代数、数论、组合题可以结合其它4个角度．但是单纯的数学文化展现并不能为学生提供独特的数学体验，合理、有效的融合和呈现方式显得特别重要．数学文化的融入方式并不是盲目的，可以结合其知识特点在现实、历史和其它学科中的应用情况等进行编制，如数论中的密码学、组合中的统筹规划、几何中的黄金分割等，这些可以增强学生的数学应用意识，同时让学生认识到数学在其它学科中的重要性，为部分学生成为日后的交叉学科人才打下基础．另外，全俄决赛试题存在着年级差异，所以在试题与数学文化的融合过程中需要结合该试题的年级特点以及学生的心智发展特点，低年级的竞赛试题中可以融入更多的社会角色和审美娱乐的内容，高年级的试题中可以适当地引入知识源流的内容．因此，要将有特色的数学文化渗透到有特点的数学知识和特定年级中去，这样数学资优生就可以更好地体验到知识的学习和文化精神的熏陶，摆脱传统枯燥单纯的知识教育[29]．

4.3 展现数学内在之美 培养资优生臻美能力

数学除了具有普适意义的美学特点外，其内在的内容、结构和方法本身就臻于大美．数学的审美价值不仅是用数学的眼光看世界，欣赏文学、美术、雕塑和音乐作品中的数学结构、数学原理之美，还应该让学生体会数学本身的美，一种纯粹的数学之美．而竞赛题，是传递这些数学之美的有效途径，正如法国著名数学家、天文学家昂利·庞加勒在《科学的价值》一书中所提到的：“数学的美感、数和形的和谐感、几何学的雅致感，这是一切真正的数学家都知道的真实的审美感……正是这种特殊的审美感，起着我曾说过的微妙筛选作用，这充分地说明，缺乏这种审美感的人永远不会成为真正的创作者．”[30]一道好的数学竞赛题可以给学生展现出数学的优雅和美丽，会让他产生对真正数学的热情[31]．在全俄决赛试题中，平面几何中几何图形的对称美、和谐美，代数不等式中的简洁美、奇异美，这些数学美都被设计者精心地编排在题目里，让学生在解题的过程中感受之美，增强他们的学习动力，提高数学学习兴趣，而这些都是在培优数学资优生时值得借鉴的．

4.4 融合文化多元特性 提升资优生国际视野

全俄决赛试题对多元文化涉及较少，27年、3个年级的试题中仅出现了2次多元文化，且都是同一类型，即古希腊的神话传说．数学作为人类文明的重要组成部分，具有文化多样性．世界上各个文明和不同的文化之间虽然有质的不同，但却是值得互相尊重、理解、学习和借鉴的[32]．数学文化同样如此，不同国家、地区、民族的人在数学创造、数学应用上都有着各自的贡献，数学文化也有着其鲜明的地域特色．在保留本民族数学的民族特色之外，还应避免狭隘的“民族主义”，应该让学生了解本民族以外的、广阔的数学天地和丰富多彩的数学文化．因此，在竞赛试题的命制时，可以有意识地融合多元文化，避免文化相对主义、保守主义，展现文化多元性和文明多样性．这样培养出来的数学英才，其视野也更开阔，更能包容世间万物的差异，更能在国际舞台上走向卓越．

[1] 阎琨，吴菡．拔尖人才培养的国际趋势及其对我国的启示[J]．教育研究，2020，41（6）：78-91．

[2] 王光明，宋金锦，佘文娟，等．建立中学数学英才教育的数学课程系统——2014年中学英才教育数学课程研讨会议综述[J]．课程·教材·教法，2014，34（5）：122-125．

[3] 单墫，葛军．国际数学竞赛解题方法·数学竞赛史话[M]．上海：上海教育出版社，2019：333．

[4] PETER J T. Future directions for research in mathematics competitions [M] // SOIFER A. Competitions for young mathematicians. Cham: Springer, 2017: 303-328.

[5] KONTOROVICH I. Problem-posing triggers or where do mathematics competition problems come from? [J]. Educational Studies in Mathematics, 2020, 105 (3): 389-406.

[6] 蒋培杰，张勇，熊斌．中外小学高年级数学竞赛试题难度的比较研究——以“华杯赛”与“袋鼠赛”为例[J]．数学教育学报，2020，29（6）：87-91．

[7] CAMPBELL J R, WALBERG H J. Olympiad studies: Competitions provide alternatives to developing talents that serve national interests [J]. Roeper Review, 2010 (1)：8-17.

[8] 张勇，何忆捷，熊斌．国际比较视角下奥数优胜者调查结果分析[J]．比较教育学报，2020（6）：83-93．

[9] 陆一，冷帝豪．中学超前学习经历对大学拔尖学生学习状态的影响[J]．北京大学教育评论，2020，18（4）：129-150，188．

[10] 朱华伟．从数学竞赛到竞赛数学[M]．北京：科学出版社，2009：47．

[11] 中华人民共和国教育部．普通高中数学课程标准（2017年版）[M]．北京：人民教育出版社，2018：2-10．

[12] 张奠宙，马文杰．简评“数学核心素养”[J]．教育科学研究，2018（9）：62-66，85．

[13] 徐瑞哲，吴潇岚．资优生培养要用好数学开放题——奥数国家队领队：过早接触数学竞赛存弊端[N]．解放日报，2021-07-19（7）．

[14] 裴昌根，宋乃庆．我国数学文化研究的文献计量分析[J]．全球教育展望，2017，46（2）：89-98．

[15] USHAKOV D V. Olympics of the mind as a method to identify giftedness: Soviet and Russian experience [J]. Learning & Individual Differences, 2010, 20 (4): 337-344.

[16] GRIGORENKO E L. Gifted education in Russia: Developing, threshold, or developed [J]. Cogent Education, 2017, 4 (1): 1-12.

[17] 张瑞炳，倪明．中国和俄罗斯高考数学考查内容比较研究[J]．数学教育学报，2016，25（2）：32-35．

[18] 阿加汉诺夫．全俄中学生数学奥林匹克[M]．苏淳，译．上海：华东师范大学出版社，2009：1-10，63-113．

[19] MARK S, DMITRI F. Russian traditions in mathematics education and Russian mathematical contests [M] // KARP A, VOGELI, BRUCE R. Russian mathematics education. Singapore: World scientific publishing company, 2010：223-252.

[20] 苏淳．全俄中学生数学奥林匹克[M]．合肥：中国科学技术大学出版社，2020：i-iii，41-80．

[21] 汪晓勤．基于数学史的数学文化内涵课例分析[J]．上海课程教学研究，2019（2）：37-43．

[22] OECD. PISA for development mathematics framework: Reading, mathematics and science [EB/OL]. (2018-09-25) [2021-02-02]. https://doi.org/10.1787/9789264305274-5-en.

[23] 熊斌，谈祥柏．趣味数学[M]．上海：上海辞书出版社，2011：1-6．

[24] 张奠宙，木振武．数学美与课堂教学[J]．数学教育学报，2001，10（4）：1-3．

[25] 徐利治．科学文化人与审美意识[J]．数学教育学报，1997，6（1）：1-7．

[26] 熊斌．数学竞赛和数学研究[M]．北京：高等教育出版社，2017：115-128．

[27] SOIFER A. The goal of mathematics education, including competitions, is to let student touch “real” mathematics: We ought to build that bridge [J]. Mathematics Competitions, 2012, 25 (2): 47-67.

[28] SOIFER A. Building a bridge I: From problems of Mathematical Olympiads to open problems of mathematics [J]. Mathematics Competitions, 2008, 21 (2): 11-18.

[29] 徐乃楠，孔凡哲，刘鹏飞．俄罗斯高中数学教科书中的数学史及其启示[J]．吉林师范大学学报（自然科学版），2013，34（4）：152-156．

[30] 庞加勒．科学的价值[M]．李醒民，译．北京：光明日报出版社，1988：383-384．

[31] SOIFER A. Goals of mathematics instruction: Seven thoughts and seven illustrations of means [M] // SOIFER A. Competitions for young mathematicians. Cham: Springer, 2017: 3-26.

[32] 徐乃楠，刘鹏飞．数学文化热：历史、意义与反思[J]．自然辩证法通讯，2020，42（8）：102-106．

Mathematical Culture in All-Russian Olympiad

LV Sun-zhong1, 2, LEI Pei-yao1, WU Yu-chi1, 2, XIONG Bin1, 2

(1. School of Mathematical Sciences, East China Normal University, Shanghai 200241, China;2. Shanghai Key Laboratory of Pure Mathematics and Mathematical Practice, Shanghai 200241, China)

The experience of Russia in mathematics competition is worthy learning, and its competition tests also have humanistic characteristics. This research mainly studies the mathematics culture in All-Russian Olympiad, and the changes of characteristics of mathematical culture between different years, content distribution, knowledge field distribution and distribution by grades are also analyzed. The following results about how to pose mathematics competition questions and how to cultivate math talents are gained. Firstly, to take the history of mathematics as a bridge to link the elementary mathematics and advanced mathematics. Secondly, in consideration of the characteristics of the knowledge field distribution, the mathematical questions should be carefully arranged to show the charm of culture. Thirdly, to use the beauty of mathematics in questions to improve the aesthetic ability of the gifted students. Last but not the least, to integrate diverse cultures to enhance the international vision of gifted students.

Russia; math competition; mathematical culture

G40–055

A

1004–9894（2022）05–0097–06

吕孙忠，雷沛瑶，吴尉迟，等．俄罗斯中学生数学奥林匹克试题中的数学文化[J]．数学教育学报，2022，31（5）：97-102．

2022–05–21

上海市核心数学与实践重点实验室课题——数学实践（18dz02271000）

吕孙忠（1991—），男，浙江温州人，博士生，主要从事数学竞赛与数学教育研究．

[责任编校：张楠、陈汉君]