小学生比例推理学习进阶模型的构建

巩子坤，程 玲，陈影杰

小学生比例推理学习进阶模型的构建

巩子坤1，程 玲2，陈影杰1

（1．杭州师范大学 经亨颐教育学院，浙江 杭州 311121；2．杭州市朝晖中学，浙江 杭州 310014）

教科书编写要按照知识的逻辑顺序与学生的认知发展顺序分层次安排教学内容，因而，厘清核心概念的学习进阶尤为重要．基于文献分析法构建假设的比例推理学习进阶模型，并据此设计问卷，测试630名一～六年级学生，修订假设的比例推理学习进阶模型，最后得到小学生比例推理学习进阶模型．该模型包含定性推理中两组量的变化、定量推理中比例的数值结构关系和数值大小关系3类进阶变量，以及对应的7个进阶水平，其中，定性推理中“双维、不确定”为最高水平．提出建议：增加教科书中定性推理的题型；开展统整定性推理与定量推理的教学设计．

小学生；比例推理；学习进阶模型

1 问题提出

义务教育数学课程标准确立了课程内容后，教科书编写就要按照知识的逻辑顺序与学生的认知发展顺序来分层次安排教学内容，因此，明晰知识的内在逻辑、学生的认知水平变得尤为重要，这就需要厘清相关核心概念的学习进阶．2004年Smith向美国国家研究理事会（National Research Council，NRC）提交的报告中首次提出“学习进阶”——“围绕一门学科的核心概念（big ideas）与原则，基于一系列连续的、复杂程度逐步提升的思维路径而形成的一种推理探究方法”[1]，而后，2007年NRC将“学习进阶”正式定义为“随着时间的推进，学生对某一学习主题的思考和认识不断丰富、深入的过程”[2]，这是当下使用最为广泛的定义．基于此，这里的“学习进阶”是指学生在较长一段的时间跨度内，学习某一核心概念（技能）时，经历的一个连续的、概念理解不断深化、思维方式不断发展的过程．国外对于“学习进阶”的研究起步较早，现研究的重点聚焦于“将学习进阶作为一种教育评价模型”[3]．构建学习进阶能帮助教师更好地认识学生的认知发展过程，从而促进学生对数学知识有更高层次的理解[4]．

比例推理贯穿小学数学的始终，与核心概念“分数”紧密相关[5]，学生在没有正式入学前，就开始潜移默化地学习比例推理．比如“一个小朋友有2个苹果，3个小朋友共有几个苹果”．比例推理是基于比和比例知识进行推理的一种能力[6]，也是根据已知信息和比例的相关性质，进行判断和计算的思维过程[5]，需要基于具体情境把握其中数量关系的变化[7–8]．国内较早的研究者苗丹民基于Noelting的4～14岁儿童比例推理认知发展的研究成果，从心理学角度将儿童比例推理能力的发展分为7个阶段[9]．而国外关于比例推理的研究主要聚焦于探究学生应用比例推理的现状，分析发现，学生难以区分问题情境中的数据结构是不是比例关系[10]；无法理解现实问题中的比例关系，进而不能正确使用比例推理解决问题[11]；对“比”和“比例”的理解过程较为困难[12]等．

目前关于比例推理学习进阶相关研究较少，北卡罗来纳大学的Confrey团队研究较具代表性．其构建的比例推理学习进阶模型聚焦于解决如何帮助学生更好地理解比例推理中量之间的关系和解题策略的问题，列举了比例推理的常见问题类型，并详细例说了如何更好地引导学生进行比例推理学习．但该研究更偏向于教学，而非指向学生比例推理的学习进阶过程．比例推理可以被视为是最为复杂的乘法思维形式[13]，Callingham等人对乘法思维，其中包括比例推理展开学习路径的相关研究，利用真实的生活情景创设评估项目，并借助Rasch模型分析项目有效性，进而确立最终的乘法思维量表[14]．而该研究更大程度上指向乘法思维，而非直接针对比例推理学习进阶．李众展以“内在比”和“相间比”为进阶变量，直接计算一～六年级学生在进阶水平上的得分，基于数据进行修订和验证，进而得到最终的比例推理学习进阶[15]．但该研究对进阶变量的选取并未细化，且数据分析方法较为单薄．

根据已有研究存在的问题，围绕小学生比例推理学习进阶模型的构建，提出以下3个研究问题．（1）假设的比例推理学习进阶模型是什么？（2）如何修订和验证假设的比例推理学习进阶模型？（3）小学生比例推理学习进阶模型是什么？

2 研究设计

2.1 研究对象

在杭州市两所普通公办小学（以下简称A校、B校）一～六年级中，从A校每个年级各随机选取两个班，B校每个年级各随机选取一个班进行测试．共发放问卷630份，回收有效问卷630份．

2.2 研究方法

首先利用文献分析法构建假设的比例推理学习进阶模型，然后根据假设的进阶模型编制相应问卷，最后利用问卷调查法对假设的进阶模型进行修订及检验，进而构建小学生比例推理学习进阶模型．

2.3 研究过程

研究分为4个阶段，具体研究流程如图1．

图1 研究流程

基于已有研究，构建假设的比例推理学习进阶模型．基于假设的学习进阶模型，开发相应的测试问卷．实施问卷测试，基于问卷数据，采用Rasch模型，对假设的学习进阶模型进行修订，得到实证的学习进阶模型．对实证的学习进阶模型进行检验，得到小学生比例推理学习进阶模型．

2.4 数据编码及计分标准

基于对比例推理的划分，将问卷分为“定性推理”与“定量推理”两部分，设置12个假设的进阶水平．其中，定性推理包含假设的进阶水平1—4，定量推理包含假设的进阶水平5—12，共33道题目．部分题目见下文．

“定性推理”部分设置为选择题，题目编码为“1.1—1.9”．每题均有且仅有唯一正确的答案，选择正确计为1分，选择错误或没选择计为0分．“定量推理”部分设置为简答题，题目编码为“2.1—2.24”．每题均有且仅有唯一正确的答案，解答正确计为1分，解答错误或没有解答计为0分．

问卷的Cronbach’s系数为0.96，表明该问卷具有较高的信度．

3 研究结果

3.1 构建假设的比例推理学习进阶模型

3.1.1 选取进阶变量

进阶变量是构成学习进阶的主要成分之一，是对学生概念理解程度的刻画与度量，也可以理解为对学生概念理解的影响因素，包括知识、能力等方面．

根据是否需要精确计算，将比例推理分为定性推理与定量推理两类．利用问题中两组量之间的比例关系，直接解决问题，而不需要进行数值计算，即为定性推理；相应地，需要利用具体数值计算才能解决问题，即为定量推理．

（1）定性推理中两组量的变化．

第一个进阶变量是定性推理中两组量的变化：如果只有一组量变化，称为“单维”；如果两组量都变化，称为“双维”．而两组量的变化情况可以细分为“变大”“不变”“变小”．如在“平均分蛋糕”的问题情境下，其中蛋糕大小和人数的变化情况均存在3种可能，两两组合共有9种情况，具体变化情况如表1．

表1 定性推理的9种变化情况

将定性推理中的9种变化情况划分为4个假设的进阶水平，从低到高排列如表2．

表2 定性推理的4个假设的进阶水平

（2）定量推理中比例的数值结构关系．

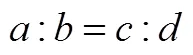
表3 定量推理中比例的数值结构关系的4个假设的进阶水平

（3）定量推理中比例的数值大小关系．

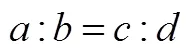
最终得到假设的比例推理学习进阶模型的3个进阶变量：定性推理中两组量的变化、定量推理中比例的数值结构关系和定量推理中比例的数值大小关系．

表4 定量推理中比例的数值大小关系的两个假设的进阶水平

3.1.2 构建假设的学习进阶模型

定性推理部分有4个假设的进阶水平．定量推理部分有两个进阶变量，组合得到8个假设的进阶水平．假设的学习进阶模型共有12个水平．对假设的进阶水平进行编码，定性推理表示为“D1”，定量推理表示为“D2”；每个类型中对应的进阶水平难度由低到高记为“L1”“L2”，以此类推如表5．

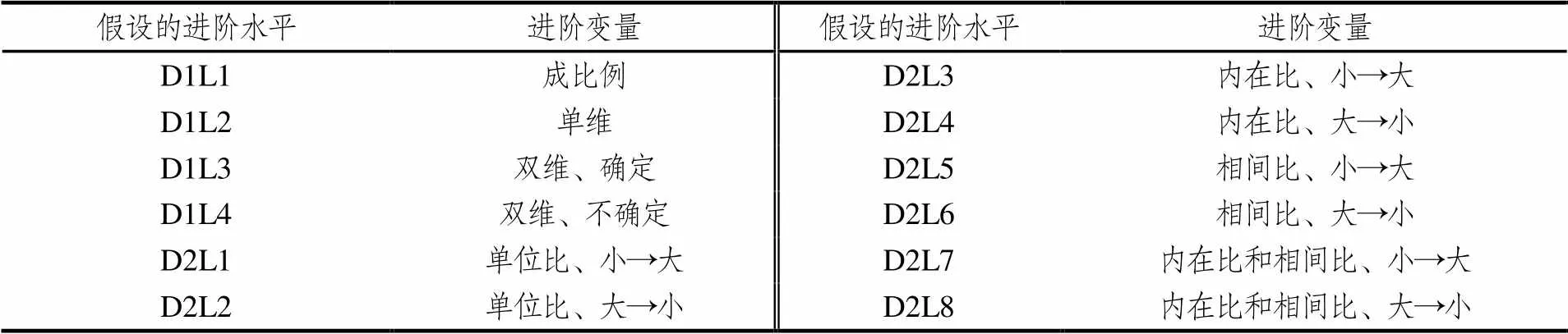
表5 假设的学习进阶模型

3.2 开发比例推理学习进阶问卷

根据假设的学习进阶模型编制的问卷包括两个部分：考察定性推理的选择题和考察定量推理的简答题．

定性推理部分采用如例题1所示的选择题进行测试．这一部分的题目不涉及具体的数值计算，其中的变化仅为任务中两组数值（蛋糕、人数）的变化，且变化情况均为“变大”“不变”“变小”3种，两组数值共得到9种变化情况，据此组合成9道测试题．

例题1 一个蛋糕平均分给8个小朋友，每人得到一块蛋糕．如果这只蛋糕变大，小朋友的人数不变，那么每个人分到的这块蛋糕与原来得到的相比（ ）．

A. 变大 B. 变小 C. 不变 D. 不确定

定量推理部分采用如例题2所示的简答题进行测试，两个进阶变量共构成8个假设的进阶水平，每个假设的进阶水平对应3道题目，共24道测试题．

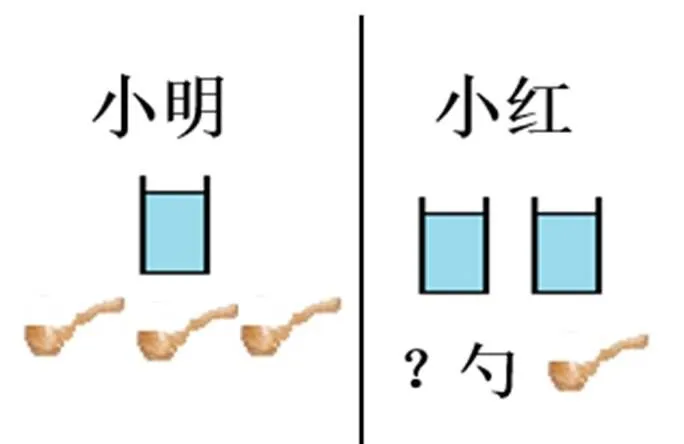
例题2 小明在大玻璃杯中加入1小杯水和3勺蜂蜜，小红在大玻璃杯中加入2小杯水，要使小红与小明的蜂蜜水一样甜，小红需要加入几勺蜂蜜？

3.3 比例推理学习进阶模型的修订

根据比例推理学习进阶问卷施测后得到的数据分析结果，对假设的学习进阶模型进行以下两步修订．

3.3.1 假设的进阶水平难度的重新排序

利用Winsteps得到每个假设的进阶水平难度的平均Rasch得分．Rasch得分越高，说明题目难度越大，对应假设的进阶水平越高．根据各假设的进阶水平的平均Rasch得分重新排列各进阶水平，得到修订后的比例推理学习进阶模型如表6．

相较于表5、表6中修订后的比例推理学习进阶模型存在两处修订．第一，定性推理中的第4个进阶水平D1L4，即“双维、不确定”是难度最大的一个水平，应排在最高的进阶水平．第二，定量推理中的第5个进阶水平D2L5的难度应该排在D2L2之后，D2L3之前．

3.3.2 合并无显著性差异的假设进阶水平

观察各假设的进阶水平的Rasch得分，D1L2和D1L3相差较小，D2L5、D2L3、D2L4、D2L6相差较小，D2L7、D2L8相差较小．若两个假设的进阶水平的Rasch得分相差较小，说明学生在这两个水平上的表现比较一致．因此，对Rasch得分相差较小的进阶水平做差异性检验，分析学生在此类进阶水平中是否处于同一水平，若学生在进阶水平上的得分无显著性差异，则将其合并为一个进阶水平．

（1）假设的进阶水平D1L2和D1L3的修订．

对学生在假设的进阶水平D1L2和D1L3的Rasch得分进行配对样本检验，发现D1L2和D1L3无显著性差异（(629)=0.332，=0.740），因此，将假设的进阶水平D1L2和D1L3合并为同一进阶水平．

（2）假设的进阶水平D2L5、D2L3、D2L4、D2L6的修订．

对学生在假设的进阶水平D2L5、D2L3、D2L4、D2L6的Rasch得分进行单因素方差分析，结果显示学生在这4个水平的得分主效应不显著（(3, 626)=0.80，=0.494）．通过多重比较发现，4个假设的进阶水平两两间均无显著性差异（值均大于0.05）．因此，将假设的进阶水平D2L5、D2L3、D2L4、D2L6合并为同一进阶水平．

（3）假设的进阶水平D2L7、D2L8的修订．

对学生在假设的进阶水平D2L7和D2L8的Rasch得分进行配对样本检验，发现学生在D2L7和D2L8上得分无显著性差异（(629)=6.377，=0.315），因此，将假设的进阶水平D2L7、D2L8合并为同一进阶水平．

3.3.3 实证的比例推理学习进阶模型

通过对假设的学习进阶模型的难度排序和进阶水平的修订，得到实证的比例推理学习进阶模型如表7．

表7 实证的比例推理学习进阶模型

3.4 比例推理学习进阶模型的验证

3.4.1 学生在不同进阶水平上得分的差异性检验

对学生在修订后7个进阶水平上的原始平均得分做单因素方差分析发现，主效应显著（(3, 626)=202.18，<0.05）．进一步多重比较发现，各进阶水平两两之间均存在显著性差异（<0.05）．因此，构建的比例推理学习进阶模型的水平划分是合理的．

3.4.2 学生在不同进阶水平上得分率的变化趋势

学习进阶模型需要符合进阶水平越高的题目难度越高，即学生的得分率越低的规律．因此计算学生在每个进阶水平上的原始平均得分率，观察得分率的变化趋势如图2．

由图2可知，学生在不同进阶水平上的得分率符合进阶水平越高得分率越低的规律，因此所构建的比例推理学习进阶模型是合理的．

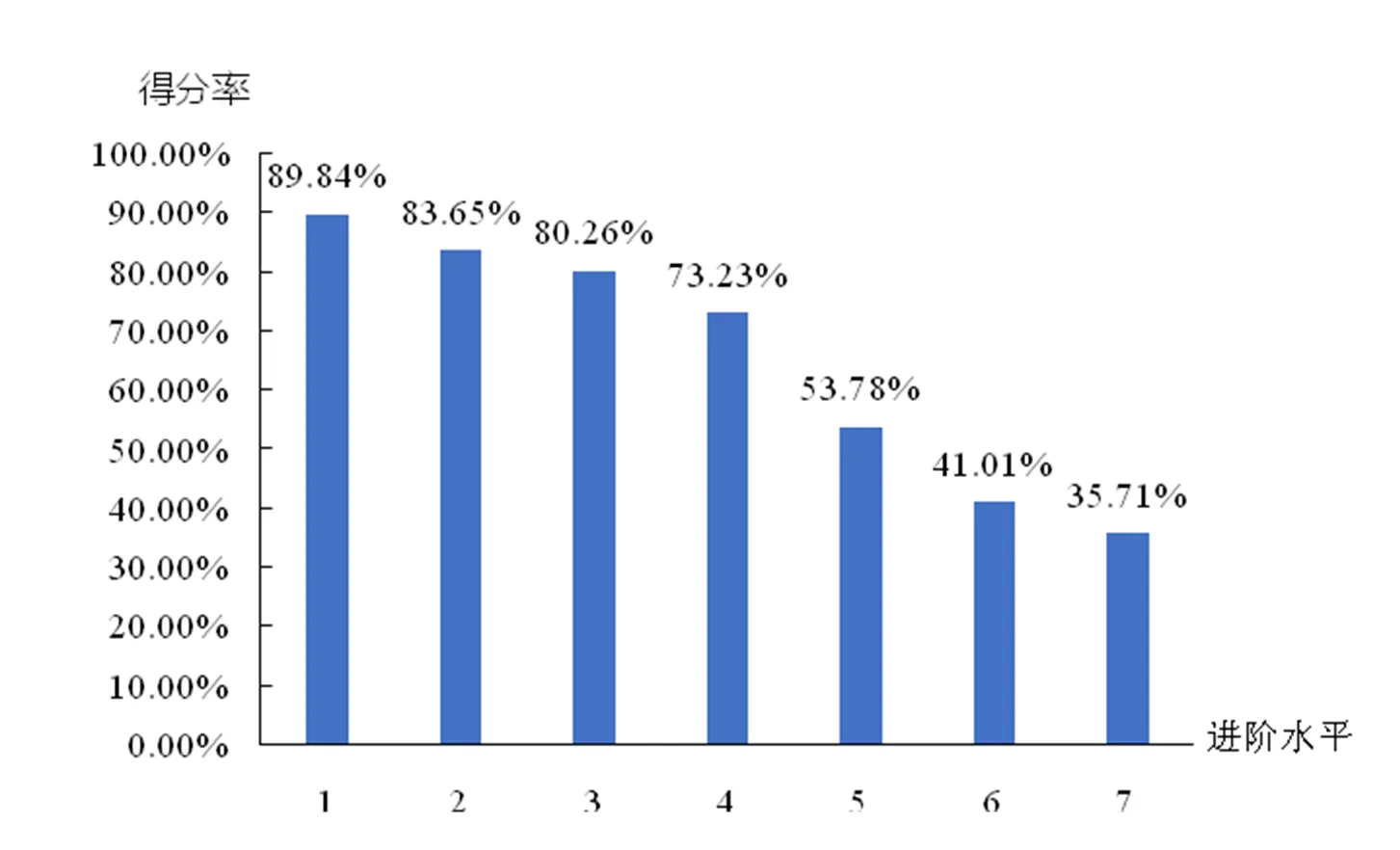
图2 小学生在不同进阶水平上的得分率

3.4.3 不同年级学生在进阶水平上的得分率变化趋势

学习进阶模型需要符合学生的年级越高，能力越高，即在每个进阶水平上的得分率越高的趋势．计算不同年级学生在不同进阶水平上的原始平均得分率，观察每个进阶水平在不同年级上的平均得分率如图3．

由图3可知，在每一个进阶水平中均符合学生的年级越高，其在该进阶水平上的得分率越高．因此，研究构建的比例推理的学习进阶模型是合理的．

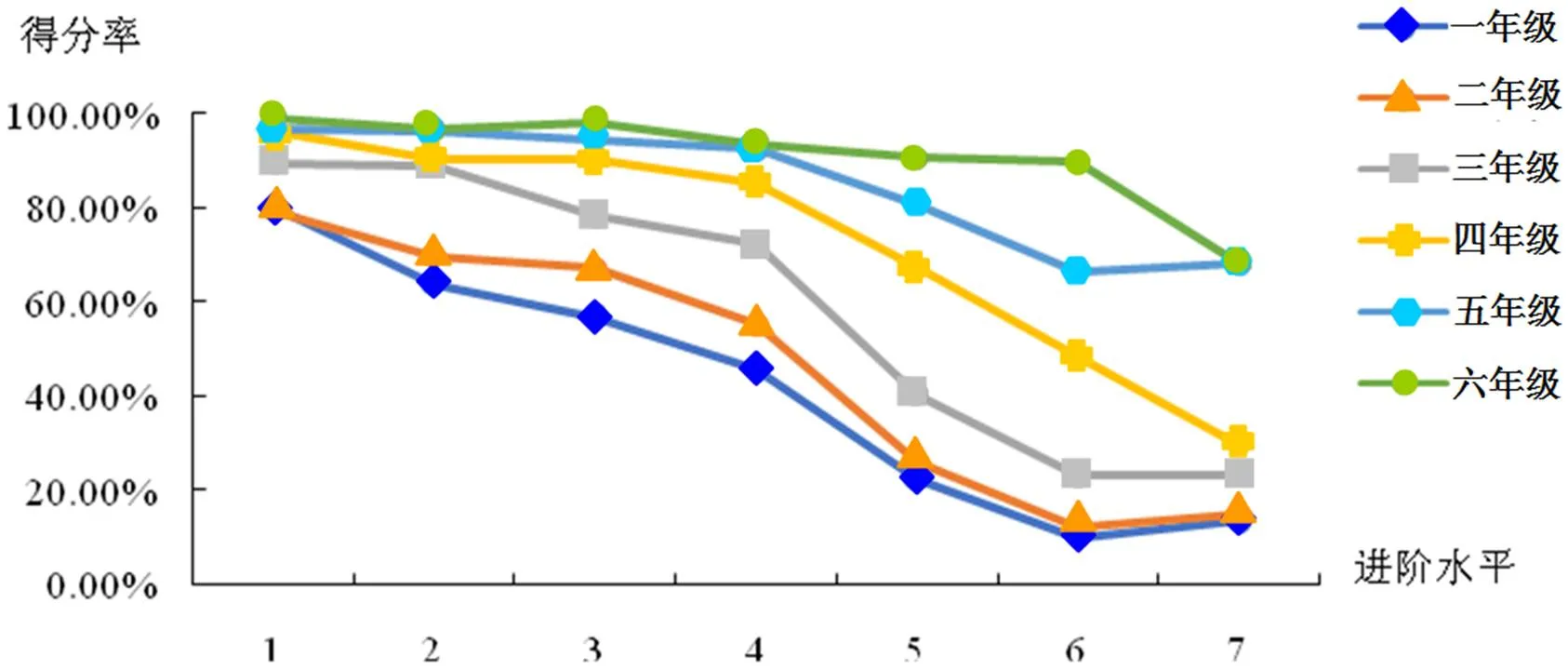
图3 不同年级学生在进阶水平上的得分率

3.5 小学生比例推理学习进阶模型

通过对假设的学习进阶模型进行修订和检验，得到实证的学习进阶模型，基于对实证的学习进阶模型的验证，得到了小学生比例推理学习进阶模型，共包含7个学习进阶水平，每个学习进阶水平对应学生具体的学习表现见图4．

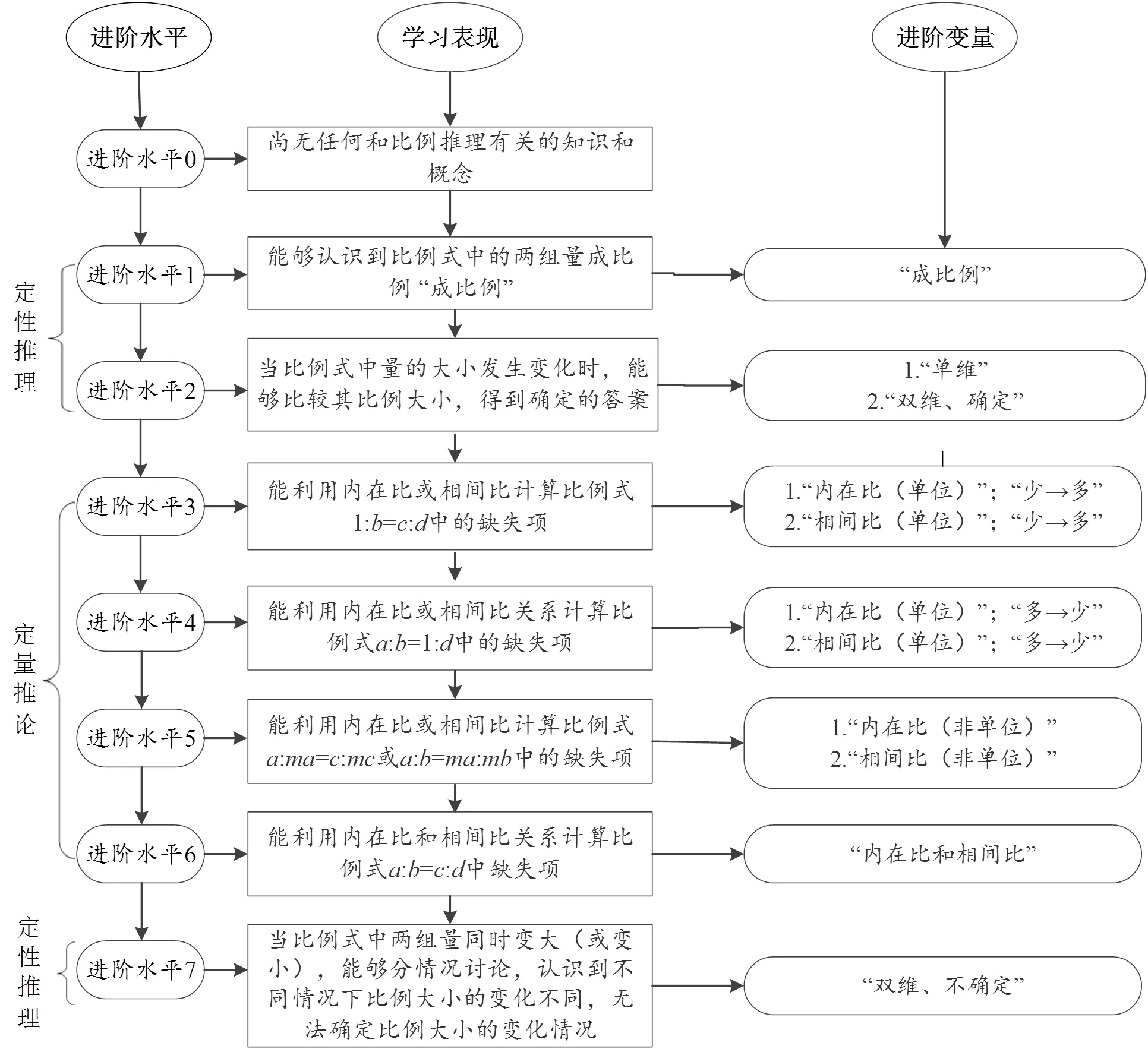
图4 小学生比例推理学习进阶模型

4 分析与讨论

4.1 创新

相对已有研究[4，11，14–15]，这里对研究方法和数据分析进行了创新．一方面，选取定性推理中两组量的变化、定量推理中比例的数值结构关系和定量推理中比例的数值大小关系作为3类进阶变量，构建小学生比例推理学习进阶模型．并利用Rasch模型对假设的学习进阶模型进行修订和验证，使得数据分析更为客观、严谨．另一方面，利用进阶模型的特点及方差分析对优化后实证的学习进阶模型进行验证，进而说明这里所构建的进阶模型符合学生的认知，更具有说服力．最终得到与已有研究不同的小学生比例推理学习进阶模型和用于测试小学生比例推理水平的问卷．

4.2 定性推理中“双维和不确定”为何是最高水平

在构建假设的学习进阶模型时，由于定性推理不需要具体的数值计算，主观地认为其涵盖的各个水平应低于定量推理，但在实际测试后发现，定性推理中“双维、不确定”这一水平的难度最高，对学生思维水平要求较高．该水平要求学生对比例式中两组量变化的3种情况进行分类讨论，进而得到最终答案．根据学生在问卷中的回答可知，大多学生在遇到此类问题时仅考虑了其中一种变化情况，并不能完整地将3种变化情况一一讨论，综合得到“不确定”这一答案，因此，定性推理中“双维、不确定”为最高水平．

4.3 假设的进阶水平合并的原因

在假设的学习进阶模型的修订过程中，对3组假设的进阶水平进行了合并．其中，定性推理中的两个水平虽然变化的情况不同，但均可以通过相同的分析方法得到结果，因此要求学生所要掌握的知识点在本质上是相同的．对于第二组的合并，学生均是通过寻找已知条件中的倍数关系，然后计算得出答案．对学生来说，倍数关系存在于内在比还是相间比之间、数值是由大推小还是小推大，都是一样的．定量推理中最高的两个假设的进阶水平在学生的解题过程中比较一致，均是先将已知比化简得到最简比，然后利用相间比得到答案，与数值的大小关系无关．

5 研究结论与建议

5.1 结论

5.1.1 比例推理学习进阶问卷

研究过程中开发了一套一～六年级学生比例推理能力问卷，可以用于评测小学生具体处于哪一个比例推理学习进阶水平．

5.1.2 小学生比例推理学习进阶模型

研究过程中构建的小学生比例推理学习进阶模型，包含2种题目类型，7个进阶水平，各水平的学习表现和进阶变量如图4．

5.2 建议

现有教科书中关于“比例推理”的内容较少，主要集中在“定量推理”；课程目标较为笼统，缺乏操作性，这就给教师的教学提出了挑战．人教版教科书中有关比例的问题题型主要集中于比例计算、化简已知比和解比例，几乎没有涉及定性推理[14–15]．学生在六年级学习“比例的基本性质”后，解决比例问题时直接列式计算，缺少进行比例推理的过程．而定性推理可以帮助学生脱离数值计算，历经并理解比例推理的全过程，提升逻辑思维和分类讨论的能力．考虑到学生的接受能力，低年级时可以增加进阶水平1及进阶水平2中对应的定性推理的题目，六年级增加进阶水平7中对应的定性推理题目．教师应根据不同的比例推理学习进阶水平与学生的认知特点，设计有针对性的课堂教学活动．

6 不足与展望

因为研究为横向调查，被试不同，所以不能有效控制无关变量对研究结论的影响．如果采用纵向追踪调查，可以更全面、真实地了解学生比例推理的发展历程，精确界定学生比例推理的进阶模型．当然，一个更加理想的做法是开展个案诊断访谈、教学实验，以探查在较为自然状态下学生比例推理的发展历程．

[1] SMITH C L, WISER M, ANDERSON C W, et al. Focus article: Implications of research on children’s learning for standards and assessment: A proposed learning progression for matter and the atomic-molecular theory [J]. Measurement Interdisciplinary Research & Perspectives, 2006, 4 (1/2): 1–98.

[2] 皇甫倩，常珊珊，王后雄．美国学习进阶的研究进展及启示[J]．外国中小学教育，2015（8）：52–59．

[3] 袁媛，朱宁波．探析国外科学教育领域的“学习进阶”研究[J]．外国中小学教育，2016（7）：59–64．

[4] CONFREY J, MALONEY A P, CORLEY A K. Learning trajectories: A framework for connecting standards with curriculum [J]. ZDM, 2014, 46 (5): 719–733.

[5] 巩子坤，杨婷，张都，等．三～六年级学生分数概念的错误理解及其发展[J]．数学教育学报，2021，30（5）：14–20．

[6] 李晓东，蔡梦婕，江荣焕．克服比例推理的过度使用——抑制控制与工作记忆的视角[J]．数学教育学报，2021，30（3）：73–77．

[7] 张侨平，邢佳立，金轩竹．小学数学教学中数学推理的理论和实践[J]．数学教育学报，2021，30（5）：1–7．

[8] 李晓东，江荣焕，钱玉娟．中小学生对比例推理的过度使用[J]．数学教育学报，2014，23（6）：73–77．

[9] 苗丹民．关于儿童比和比例概念发展的研究（综述）[J]．心理学动态，1991（1）：18–23．

[10] ARTUT P D, PELEN M S. 6th grade students’ solution strategies on proportional reasoning problems [J]. Procedia- Social and Behavioral Sciences, 2015 (197): 113–119.

[11] SUSAN, LAMON. Ratio and proportion: Connecting content and children’s thinking [J]. Journal for Research in Mathematics Education, 1993, 24 (1): 41–61.

[12] WATANABE L T. Developing ratio and proportion schemes: A story of a fifth grader [J]. Journal for Research in Mathematics Education, 1997, 28 (2): 216–236.

[13] HILTON A, HILTON G, DOLE S, et al. Promoting middle school students’ proportional reasoning skills through an ongoing professional development programme for teachers [J]. Educational Studies in Mathematics, 2016, 92 (2): 193–219.

[14]  CALLINGHAM R, SIEMON D. Connecting multiplicative thinking and mathematical reasoning in the middle years [J]. The Journal of Mathematical Behavior, 2021, 61(1): 100 837.

[15] 李众展．一～六年级学生比例推理的学习进阶研究[D]．杭州：杭州师范大学，2019：22–53．

[16] 中华人民共和国教育部．义务教育数学课程标准（2022年版）[M]．北京：北京师范大学出版社，2022：27–30，63．

[17] 人民教育出版社，课程教材研究所，中学数学课程教材研究开发中心．义务教育教科书数学六年级上册[M]．北京：人民教育出版社，2014：48–56．

[18] 人民教育出版社，课程教材研究所，中学数学课程教材研究开发中心．义务教育教科书数学六年级下册[M]．北京：人民教育出版社，2014：40–67．

Construction of the Learning Progression Model of Proportional Reasoning for Elementary School Students

GONG Zi-kun1, CHENG Ling2, CHEN Ying-jie1

(1. Hangzhou Normal University Jing Hengyi School of Education, Zhejiang Hangzhou 311121, China;2. Hangzhou Zhaohui Junior High School, Zhejiang Hangzhou 310014, China)

Textbook compilation needs to arrange the teaching contents hierarchically according to the logical order of knowledge and the cognitive development order of students. Therefore, it is particularly important to clarify the learning progression of core concepts. This study constructs the hypothetical learning progression model of proportional reasoning through literature analysis, designs a questionnaire, and surveys 630 students in grades one to six. Based on the questionnaire data, the hypothetical learning progression model of proportional reasoning was revised and validated, and the learning progression model of proportional reasoning for elementary school students was proposed. The model includes three types of variables and the corresponding seven levels. The variables are as follows: the change of two groups of quantities in qualitative reasoning, the numerical structure relationship of proportion and the numerical size relationship in quantitative reasoning. Among the seven levels, “two dimensions and uncertain” is the highest level in qualitative reasoning. The following suggestions are put forward: increasing the types of questions for qualitative reasoning in textbooks; carrying out the teaching design of integrating qualitative reasoning and quantitative reasoning.

elementary school students; proportional reasoning; the model of learning progression

G622

A

1004–9894（2022）05–0048–06

巩子坤，程玲，陈影杰．小学生比例推理学习进阶模型的构建[J]．数学教育学报，2022，31（5）：48-53．

2022–08–10

浙江省哲学社会科学规划课题——基于认知发展模型的义务教育教科书编写质量提升研究

巩子坤（1966—），男，山东滕州人，教授，博士生导师，主要从事数学教育心理研究．

[责任编校：周学智、张楠]