A new approach for free vibration analysis of a system of elastically interconnected similar rectangular plates

E.Heidari and A.Ariaei

Department of Mechanical Engineering,Faculty of Engineering,University of Isfahan,Isfahan 8174673441,Iran

Abstract: A new procedure is proposed to ease the analyses of the free vibration of an elastically connected identical plates system with respect to Kirchhoff plate theory.A structure of n parallel,elastically connected rectangular plates is of concern,whereby the motion is explained by a set of n coupled partial differential equations.The method involves a new change in variables to uncouple equations and form an equal system of n decoupled plates,while each is assumed to be elastically connected to the ground.The differential quadrature method is adopted to solve the decoupled equations.To unravel the original system,the inverse transform is applied.Decoupling the equations enables one to solve them based on the solution methods available for a single plate system.This also diminishes the computational costs of such problems.By considering different boundary conditions,a case study is run to present the method and to validate the results with its counterparts,for which excellent agreement is observed.Assessing the influence of dimensionless thickness,aspect ratio,and stiffness coefficients on the frequencies reveals the different effects of them at the low order of dimensionless natural frequencies in comparison with high orders and for different boundary conditions.

Keywords: multiple-plate system;elastic connections;free vibration;Kirchhoff plate theory;differential quadrature method

1 Introduction

Consisting of different continuous systems,coupled structures are highly applied in engineering fields;consequently,there exist many studies concerning them in the field of mechanical behavior.The complexity of coupled structures centers on their feature of having continuous components.Coupled structures consisting of beams are one of these systems which have received much attention during these years (Del Carpioet al.,2017;Jouneghani and Haghollahi,2020;Ketiyot and Hansapinyo,2018;Liet al.,2020;Liuet al.,2020).Many studies of this category have been done on the elastically connected double and multiple beam systems.The interaction between external moving loads and multiple beams systems is the subject of a study run by Foroozandeh and Ariaei (2018).By applying the Timoshenko beam theory,they assessed the effects of inertia and different types of acceleration on system response.There are similar studies in which this issue is assessed (Ariaeiet al.,2011;Paunovićet al.,2020;Fenget al.,2020).Britoet al.(2019) applied the boundary element method (BEM) to analyze a double beam system,in which the Winkler foundation theory is compared with that of Pasternak.Liu and Yang (2019)and Zhaoet al.(2020) provided a closed-form solution for the free and forced vibration of double beam systems,in which the main feature is applying Green′s functions.

Double and multiple plate systems are other types of complicated coupled structures,which have many applications.In absorbing the vibration of large deck plates of ships,bridges,optical tables,computer disk drives,hard drives,multi-array drives of computer servers,and general tooling machines,the double plate systems are highly contributive and feasible.Next to the practical problems in construction and the complexities in solving the equations as limitations,there also are advantages in designing lightweight structures that represent excellent practical fields in structural engineering,such as in aeronautical and mechanical engineering.Double and multiple plate systems are observed in the aerospace industry,for example,space platforms,solar panels,and the skin of planes′ wings(Giles,1995).In civil engineering,solutions obtained from theoretical approaches of this type of structure can be applied for estimating the behavior of multi-story buildings (Stojanovićet al.,2015).Arthi and Jaya (2020)studied the seismic performance of a double concrete plate system consisting of a shear wall and a slab to provide a seismic resistant connection for precast elements used in the structure.Multi-plate systems can be applied to reduce the seismic effect on various structures.Li and Shu (2020) applied Triangular-plate added damping and stiffness (TADAS) device which is a multiple triangular plate system.Maleki and Dolati (2020) applied the multi-plate system as the end diaphragm in the tub girder of bridges to reduce seismic demand by more than 25%.Multiple plate systems can also be used to simulate the dynamic behavior of multilayer soils (Chaoet al.,2020;Liet al.,2018),wherein the multi-degree of freedom(MDOF) analysis method can be applied to simplify the solution.Applying powerful methods such as Rayleigh_Ritz,finite element,transfer matrix,etc.,for solving complex geometries is feasible.However,simplifying complex structures by the inclusion of coupled identified structures such as plates,beams,etc.,in reducing the calculation effort has been assessed by some researchers.One of the most well-known structures of this type is laminated composite materials that may be modeled as a structure consisting of several plates connected by elastic or viscoelastic soft material.In case intermediate layers have negligible mass and a shear modulus;one can only take into account their compressibility and model this type of laminate by applying the method proposed in this article.This leads to having only normal stress,with no need to fulfill the continuity conditions in the shear strains in various layers′ interfaces,which results in a simplification of equations and the computational process.A high strength and stiffness-toweight ratio of laminated composite materials provide major reasons for applying them in a wide variety of mechanical and civil engineering systems such as the aircraft,automobile,train,and construction industries.As to energy harvesters,inserting piezoelectric layers in such combinations has become intriguing in scientific community harvesters (Yuanet al.,2017;Khazaeeet al.,2020;Fuet al.,2020;Tianet al.,2020;Liuet al.,2020).

The concept of the coupled plate systems field was applied by McElman (1964),who assessed the flutter of a simply supported double plate system,subject to a combination of mid-plane loads and aerodynamic pressure by assuming a quasi-static condition (high Mach number) and not considering the damping term.McElman also drew some sketches,illustrating system buckling behavior.In a similar study,Bismark-Nasr(1977) applied the FE method to explain the stability features of the same system,in which the damping term of aerodynamic pressure was of concern.By adopting the Winkler foundation theory,Kunukkasseril and Swamidas (1973) and Swamidas and Kunukkasseril(1975,1978) assessed the free vibrations of elastically connected circular plate systems.Kunukkasseril and Swamidas (1975) also introduced an analytical solution for the stability of circular double plate systems with different boundary conditions.The Kirchhoff plate theory was applied by Chonan (1976,1979a) to assess the free vibration of elastically connected multiple circular and annular plate systems subjected to elastic boundary conditions,by which an attempt was made to classify the mode shapes and consider the effect of in-plane loads on natural frequencies.In other studies carried out by Chonan (1979b,1979c),the Kelvin model was applied to analyze the stability of double Mindlin rectangular plates connected by a viscoelastic medium subject to a moving load.With reference to internal material damping and based on Mindlin plate theory,the forced vibration of an annular double plate system with different boundary conditions was assessed by Irieet al.(1982).A method based on Green′s functions was proposed by Kukla (1998,1999) to solve the free vibration of a system consisting of two plates connected by a continuous and discontinuous Winkler medium;it was revealed that the elastic connection size affects system frequencies.By applying the classical Navier method,the natural frequencies of an elastically connected double plate system were determined by Oniszczuk (2000) and a comparison was made with a double membrane system to establish their similarity.This study was extended by Oniszczuk (2004) to embody forced vibration and to illustrate that the second plate can behave as a dynamic vibration absorber.Applying the double plate configuration in absorbing and reducing vibration has been of significant concern in many studies(Aidaet al.,1995;Wang and Chen,2013;Wang and Lin,2016;Kamenskikh and Lekomtsev,2020).Hedrih(2006,2007,2008) and Hedrih and Simonović (2012)assessed the free and forced vibration of rectangular and circular double plate systems by applying Kelvin foundation theory subject to discontinuity in the elastic medium,nonlinearity,and different boundary conditions assumptions.The effect of connecting rolling viscous nonlinear elastic elements on the forced vibration of a double plate system was assessed by Simonović(2012),whereby it was revealed that rolling elements inertia intensified resonant transition phenomena.The intersection between a double plate system and soil(as a connecting medium) by applying the Winkler and Pasternak foundation theory was modeled by Rosa and Lippiello (2009) to analyze the free vibration of the system subject to simply supported boundary conditions.The coupled plate systems are applicable in the fuel assembly of reactors and heat exchangers,and their oscillating behavior was studied (Jeong,2006;Jeong and Kim,2009;Jeong and Kang,2013;Bochkarev and Lekomtsev,2016).Maet al.(2014) proposed an active triple-panel sound insulation system with a controllable force acting on the middle plate.An analytical method was adopted by Sadri and Younesian (2016) in assessing the vibrational and acoustic responses of a sandwich plate coupled with an enclosure cavity,by which it was assumed that the resilient material between the layers was of a Winkler medium and it was found that cavity thickness had a reverse effect on plate frequencies.The connecting resilient material effect on the stability behavior of a cross-ply laminated plate was studied by Stojanovićet al.(2019),whereby the viscoelastic assumption was applied for the connecting material.Stojanovićet al.(2015) assessed the vibrational and stability behavior of multiple plate systems by applying the Winkler foundation theory.When the thickness of the plate is small compared to its other dimensions,the Kirchhoff plate theory is applied,whereby the effects of rotary inertia and shear deformation are ignored.For thick plates,however,the Mindlin plate theory was applied (Rao,2007).Although,when considering thin plates,the Kirchhoff plate theory is of concern in this article;nonetheless,the proposed method can be extended to higher-order plate theories such as that of Mindlin.

Because exact solution methods are not always available,approximate numerical methods (Abdel Raheemet al.,2018;Bendineet al.,2016;Dusickaet al.,2004;Guet al.,2018;Liuet al.,2016;Luet al.,2004;Tahounehet al.,2019,2020;Wu and Zhong,2003) are preferred.However,due to the accuracy and the convenience of doing parametric studies,applying analytical and semi-analytical solutions (Busby and Weingarten,1972;Ebrahimi and Heidari,2019;Lobitzet al.,1977;Nayfehet al.,1974;Bayat and Pakar,2013;Wang,2018;Wanget al.,2020;Wanget al.,2019;Wang and Zhao,2019;Wang and Zu,2017a,2017b;Yang and Wang,2020) are more appropriate.By applying an analytical procedure,a new approach is proposed to uncouple the governing equations of multiple-plate systems to enable one to solve them based on the solution methods available for a single plate system;thus,there is a reduction in the computational costs of such coupled problems.

In the referenced articles for coupled beam and plate systems,a double-plate system connected by an elastic layer,a multiple-plate system in a sandwich structure,or a system of elastically connected beams are often studied.Simultaneously solving the governing equations of coupled plate systems is essential,wherein calculations are time consuming,especially when the number of plates increases.By consideringnelastically,interconnected rectangular plates,a new method involving a change in variables is proposed to uncouple a set ofnpartial differential equations into independent ones and to extend the work done by Ghafarian and Ariaei(2016),wherein a multiple beams system is of concern.This leads to converting and reducing the solution of elastically interconnected plates to the solution of independent plates with a slight computational effort,which is especially evident for many plates.Another additional feature is the second moment of mass,which is absent in some references for thin plates.The necessity of identical plates and identical boundary conditions on the same side is the only restricting assumption for this method.

This article is organized as follows: the problem formulation is introduced in Sec.2;results and discussions are presented in Sec.3,and the conclusion appears in Sec.4.To represent this technique in detail a case study with three plates is discussed in Sec.3;frequencies and mode shapes are acquired;and several parameters′ effects,such as dimensionless thickness,aspect ratio,and layers stiffness coefficients,are listed in several tables and figures.

2 Problem formulation

2.1 Differential equations of motion

A system ofnelastically connected,rectangular Kirchhoff plates,joined continuously by elastic layers,is assumed,as shown in Fig.1.The length,width,and thickness of each plate area,bandh,respectively.Without affecting the solution approach,all plates of the system are assumed to be clamped on one side and free on the other (the C-F-F-F boundary condition).The Winkler layer has the linear stiffness coefficients ofk,the displacements are minor,and the material is homogeneous and isotropic.

Fig.1 Schematic of a system of n elastically connected rectangular plates

Based on Kirchhoff plate theory,the straindisplacement equations,constitutive equations,and Hamilton principle (Reddy,2006),the vibration equation for one plate is expressed as:

where,iwis the transverse deflection ofith plate,kiis the stiffness of the elastic medium between the (i-1)th andith plate,I0=hρis the mass density per unit area of the plate surface (the zero-th moment of mass),andI2=ρh3/12 is the second moment of mass.

The parameterDis defined as:

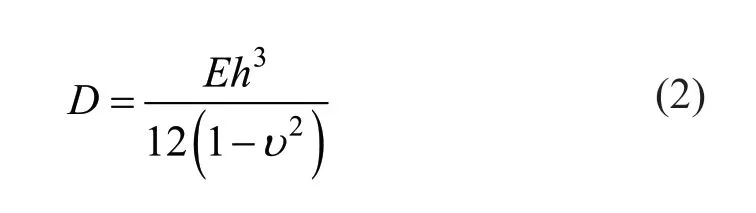
where,ρ,Eandυare the density,Young′s modulus,and the Poisson′s ratio,respectively.To apply these to the first and last plate,w0,wn+1,andkn+1values are set to be zero in Eq.(1).

The boundary condition of theith plate is expressed as (Reddy,2006):

y=0,b(Free)

At the corner of the two adjacent free edges,the following equation is applied for the boundary condition(Reddy,2006;Shu,2012):

2.2 Decoupling of the equations of motion

That Eq.(1) forms a system ofncoupled,partial differential equations that are not easily solvable is evident.Through a correct manipulation of the variables the equations of motion are uncoupled,which would enable solving them separately in a straightforward manner.By reversing the method,the anticipated parameters of the original system,such as the natural frequencies and the mode shapes become extracted.The new variableupis defined by (Ariaeiet al.,2011;Ghafarian and Ariaei,2016):

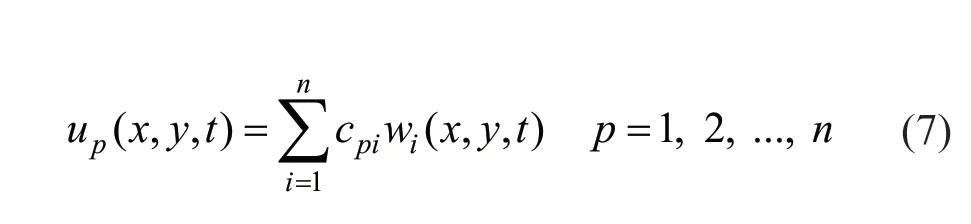
where,pis the plates′ count (p=1,2,…,n).The coefficientscpishould be identified in a manner as to uncouple thce equations.Multiplying theith equation bycoefficientpiand then adding them would yield:

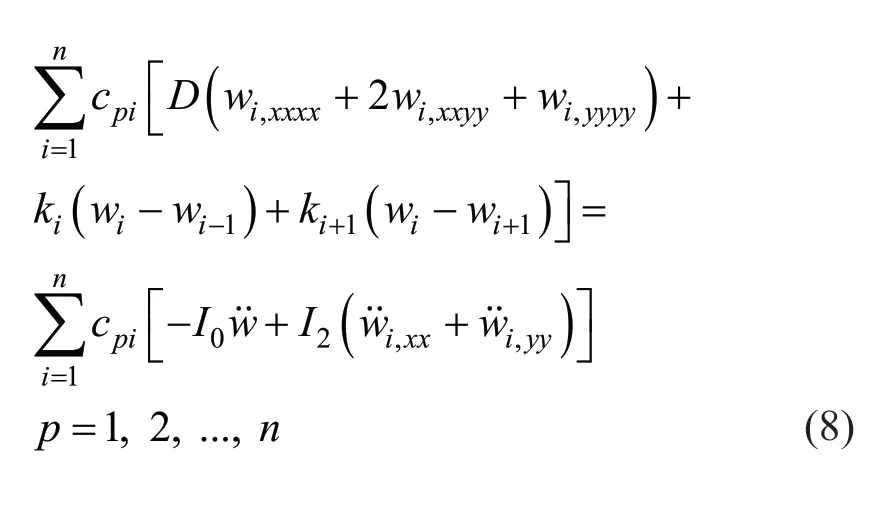
By considering Eq.(7),Eq.(8) is rewritten as:

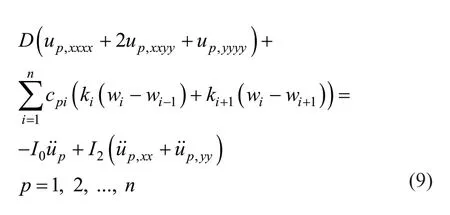
In a similar manner,the new equations for boundary conditions Eqs.(3)-(6) are expressed as:

x=0 (clamped)

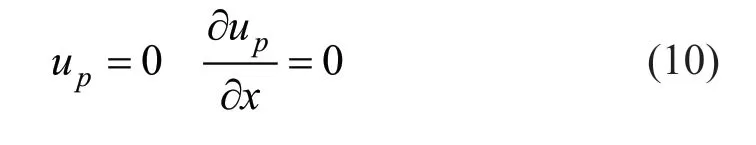
x=a(Free)

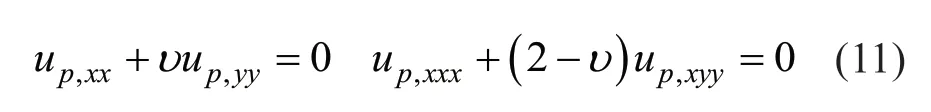
y=0,b(Free)

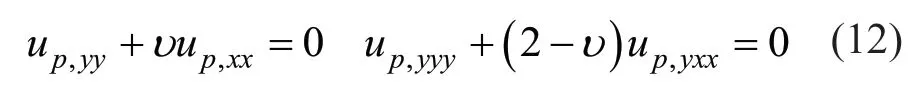
and at the free corners:

In rewriting thepth equation in Eq.(9),by considering only one function ofu p(x,y,t),a decoupled set of equations would yield,provided that the following equation holds:

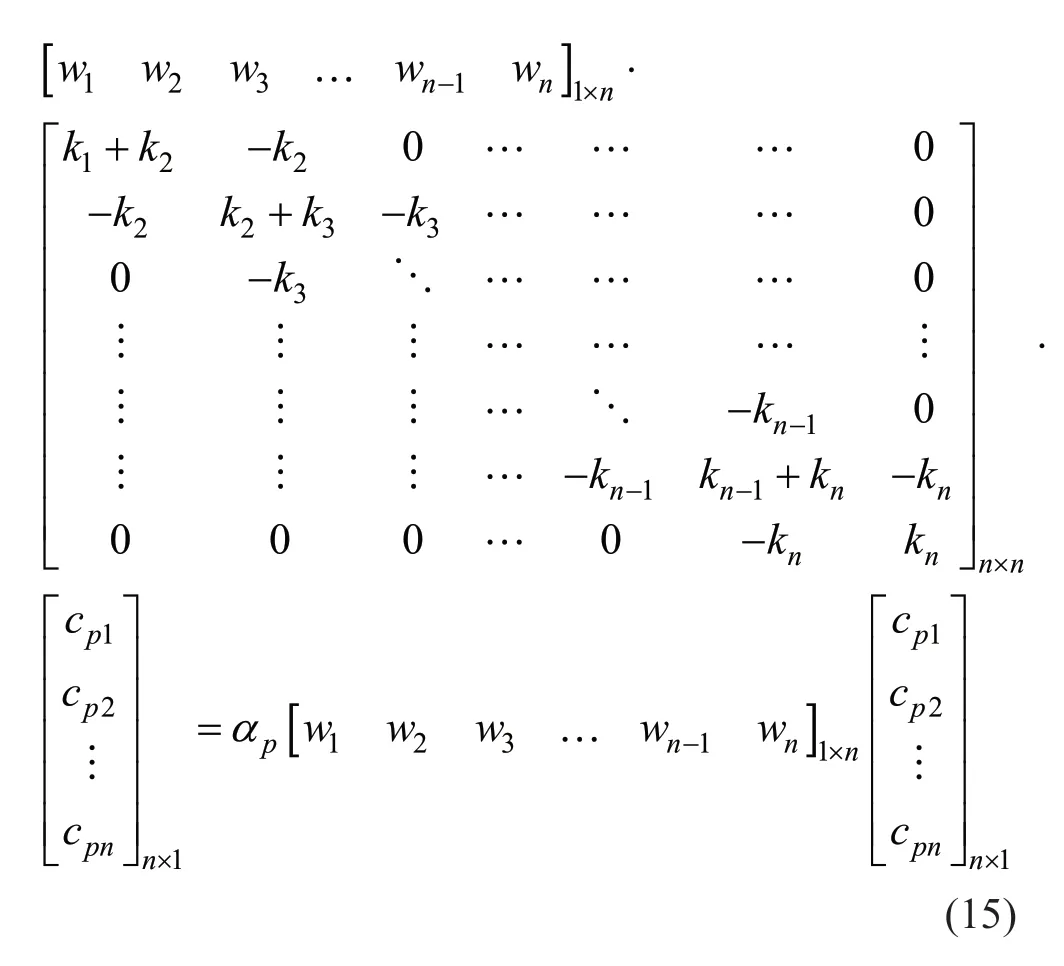
By inserting Eq.(7) in Eq.(14) with some rearrangements,Eq.(15) is arrived at,as follows:

As to the independency of the functions ofiw(i=1,2,…,n),to satisfy Eq.(15),it is essential to have:

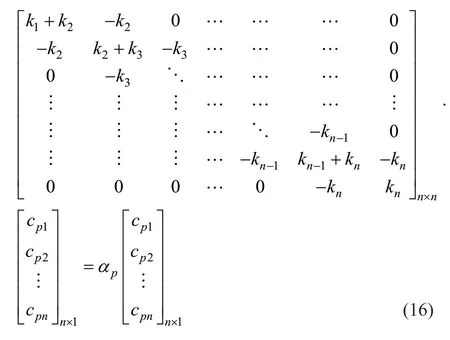
In matrix notation,Eq.(16) is expressed as:

where,Iis the unit matrix and matricesKandcpare defined through:

Equation (17) is an eigenvalue problem whereinpαandcpare thepth eigenvalue and eigenvector of MatrixK,respectively.To have a nontrivial solution it is necessary that:

The eigenvalues of matrixKobtained through Eq.(19) are applied to extract the corresponding eigenvectors from Eq.(17),the components of which are the coefficients shown in Eq.(7).By applying these eigenvectors in defining the new variableu p(x,y,t),the equations are uncoupled;that is,the existence ofαpvalues andcpvectors assure that Eq.(9) is uncoupled.By applying Eq.(14) in Eq.(9),the new decoupled equations are expressed as:

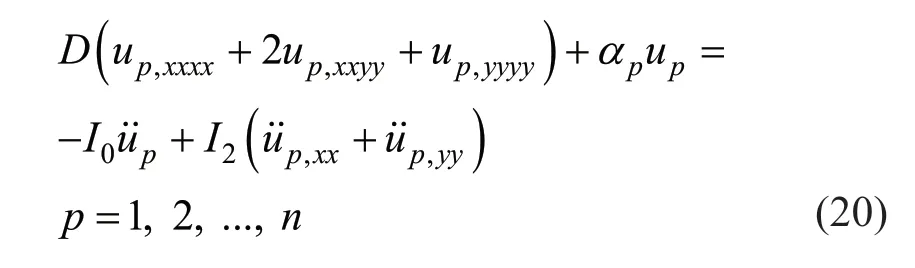
Equation (20) and boundary conditions Eqs.(10)-(13)constitute a new system ofnseparated plates with no mutual interaction.Figure 2(b) shows a schematic of this new system.Here,the original system consisting ofnconnected plates is transformed into a system ofndecoupled plates,where thepth plate independently appears on a Winkler foundation with the spring coefficientpαelastically connected to the ground,as shown in Fig.2.In other words,the decoupled plates system pictured in Fig.2(b) is a mathematically obtained system related to Eq.(20),with boundary described in Eqs.(10)-(13).The same method is adopted in solving the uniform Eq.(20).By applying the reverse transformation,the original system’s solution is obtained.

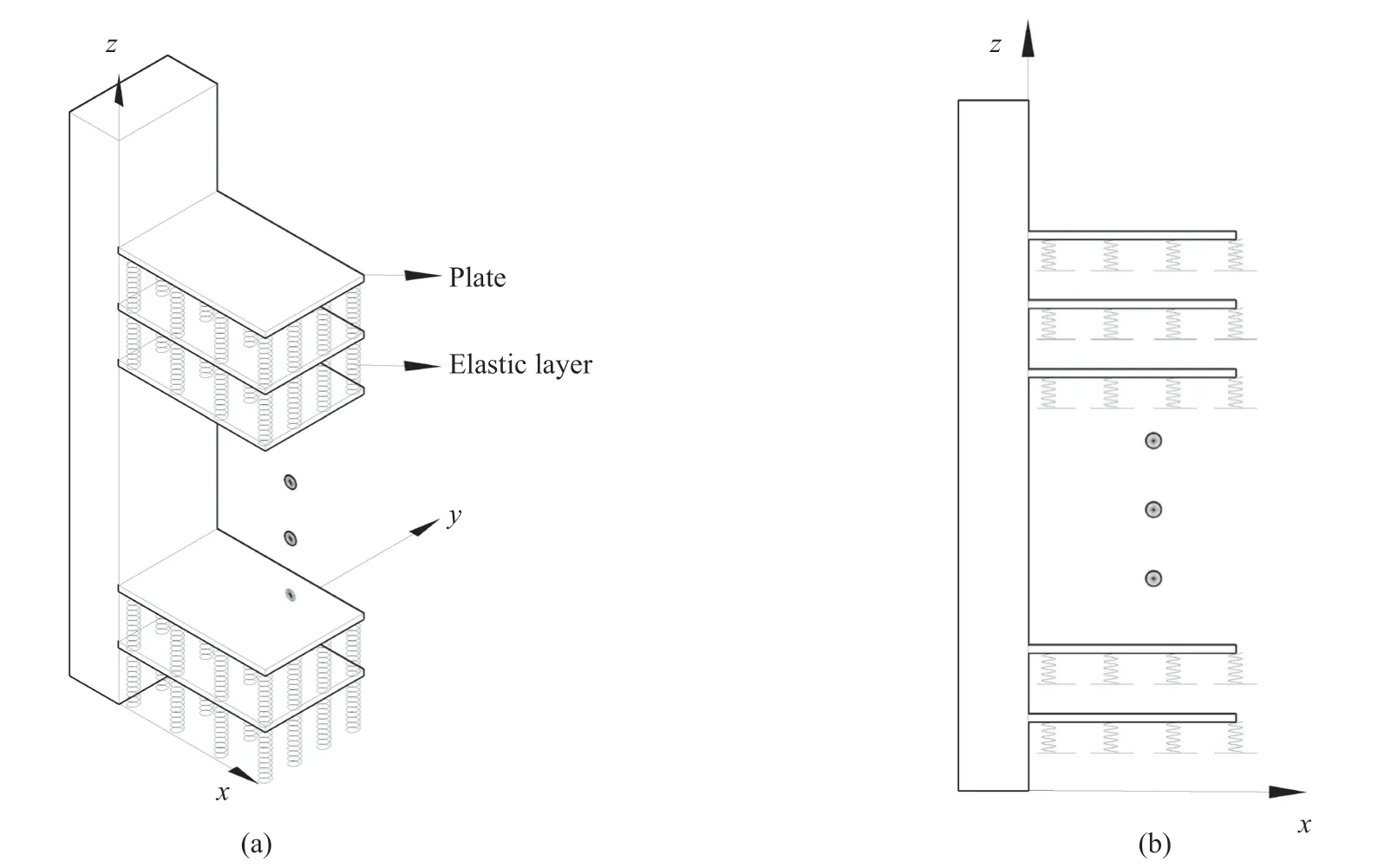
Fig.2 The transformation from the coupled plate system to the decoupled plate system.(a) Coupled plate system,(b) decoupled plate system

2.3 The free vibration problem

To solve Eq.(20),the following harmonic motion is considered as follows:

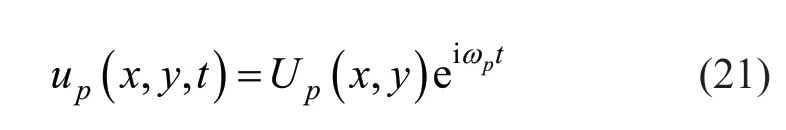
where,U p(x,y) andωpare the amplitude and natural frequencies of thepth plate,respectively.

To simplify the formulas,the following dimensionless parameters are introduced:

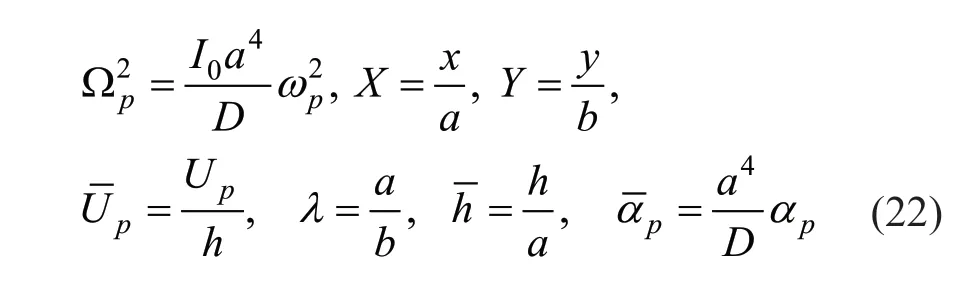
Inserting Eq.(21) into Eq.(20) and applying the dimensionless parameters of Eq.(22),yield:

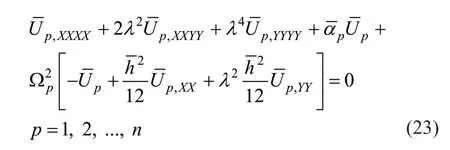
By applying a similar method for Eqs.(10)-(13),the dimensionless boundary conditions are obtained as:

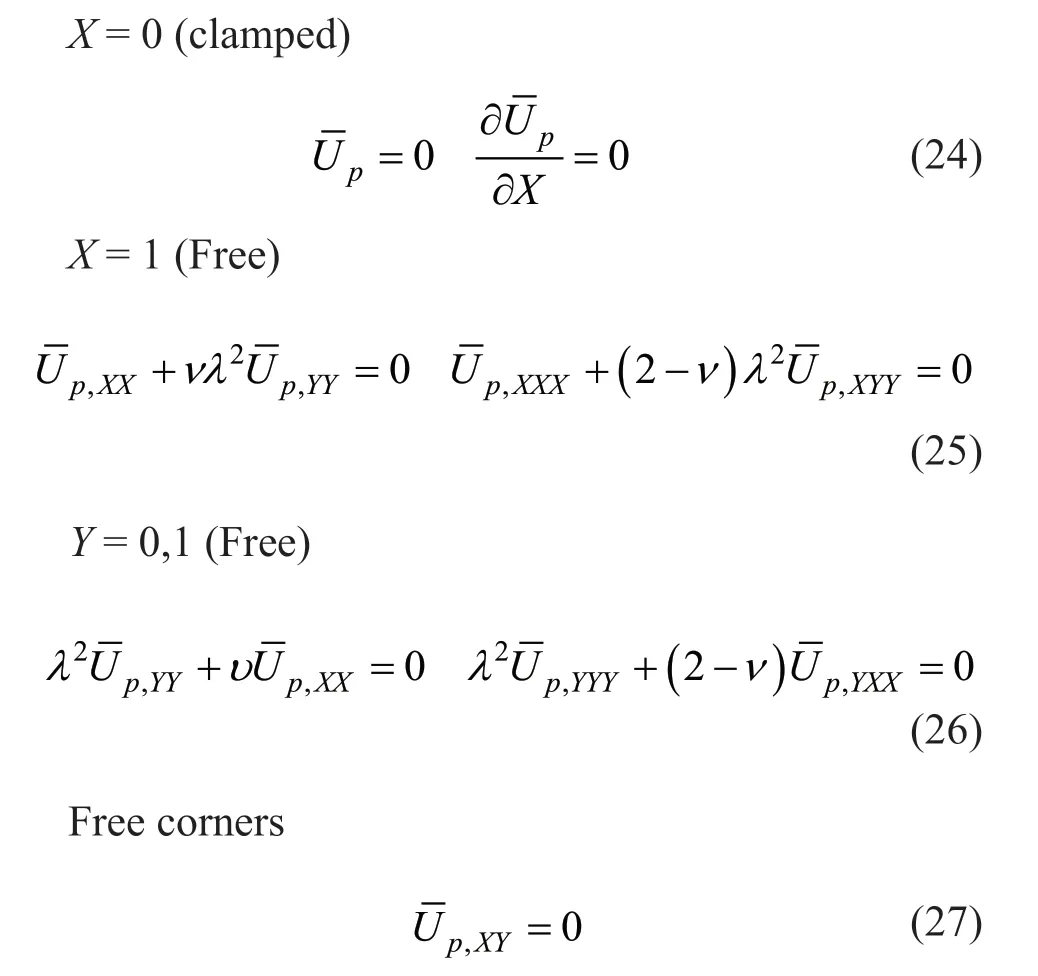
The solution of Eq.(23) by considering boundary conditions Eqs.(24)-(27) leads to obtaining the frequencies and modes of thepth plate in the decoupled plates system.Each natural frequency in the decoupled plates system is one of those found in the original system.By back-substituting them in Eq.(21) and then using that result into Eq.(7),the original system′s modes are found.Equation (7) is rewritten in a matrix notation as:

where,

Possessing the variableu p(x,y,t),the original system′s variableswi(x,y,t) are calculated through the use of the following equation:

where,

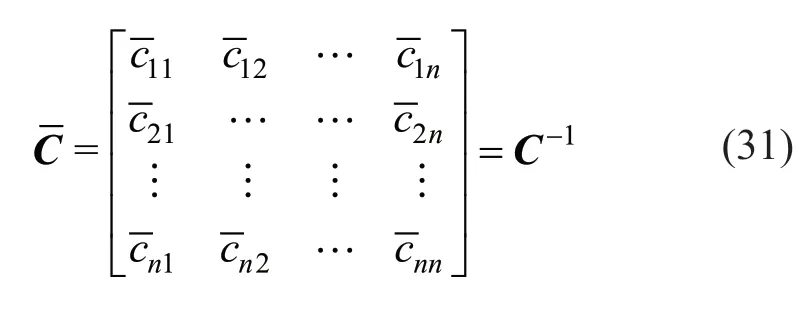
Because the rows of matrixCare the eigenvectors of the symmetric matrixKand are linear independent,matrixCis invertible.

By applying Eq.(30),the vectorWof the original system is obtained from the vectorUof the decoupled plate system.As thepth plate of the decoupled plate system becomes oscillated at itsjth natural frequency and mode shape (i.e.,Upj(x,y),ωpj),Eqs.(21)and (30)reveal that all plates of the original system vibrate at the same frequency,ωpj,which is the natural frequency of the original system,displayed in Fig.1.The corresponding mode shape of the frequencyωpjof the original system is obtained by settingU pj(x,y) in Eq.(30).

2.4 Solution procedure

As an efficient numerical method,the differential quadrature method (DQM) is applied to solve the governing equations of motion obtained in the previous section.Compared to the conventional low order f inite difference and f inite element methods,the DQ method can result in accurate numerical results by applying a smaller number of grid points;therefore,some computational effort is required (Shu,2012).However,both the convergency and stability of the solution are intensely dependent upon the distribution of sampling points.Consequently,the well-known Chebyshev nodes are served to discretize the governing equation of motion and the boundary condition expressions,as follows:

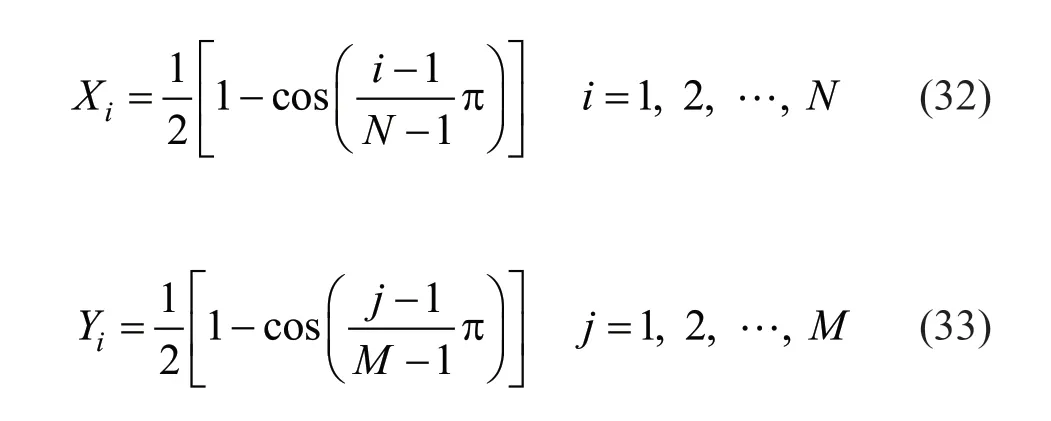
In a rectangular plate,a grid ofN×Mpoints is developed.By applying the weighting coefficient,a discretized equation is provided for every point of the grid,to which the following approximation is applied in the governing and boundary equations:

where,NandMare the number of the sampling points in thexandydirections,respectively.are the weighting coefficients of thenth derivative off(x,y)with respect toxand themth derivative off(x,y) with respect toy,respectively (Shu,2012).With the aid of Eqs.(32)-(35),Eq.(23) can be discretized as follows:

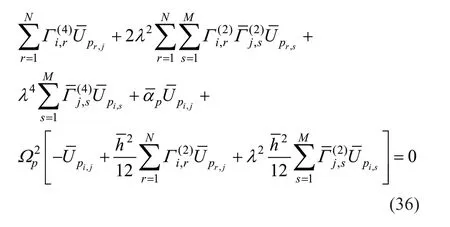
A similar approach is applicable to discretize boundary conditions Eqs.(24)-(27) as follows:

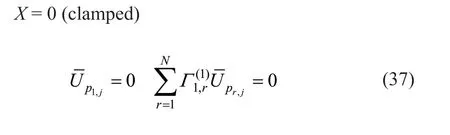
For mixed boundary conditions,the weighting coefficients are combined in a piecewise function (Shu and Wang,1999).The discretized Eqs.(36)-(40) can be vectorized (Liu and Trenkler,2008) and assembled in the following form:

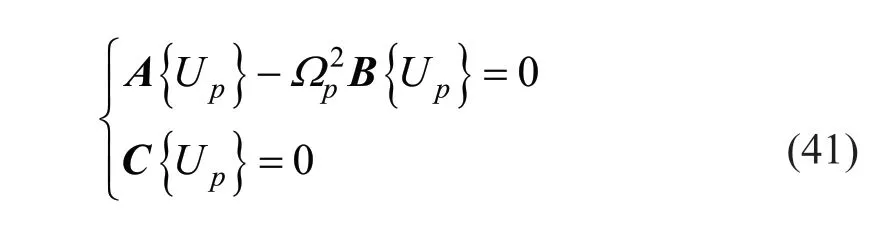
where {Up} is the vectorized arrangment ofvalues.The Eq.(41) is combined by applying the “general approach for implementing boundary conditions” (Shu,2012) and can be solved by using common matrix algebra.

The lower computational cost of the method proposed for decoupling the equations of motion can be revealed through operations-additions and multiplications required to obtain the natural frequencies,where a determinant should be calculated.Dubbs and Siegel (1987) presented an equation for computing the operations-additions and multiplications required for obtaining anm × mdeterminant by way of cofactor expansion expressed as:

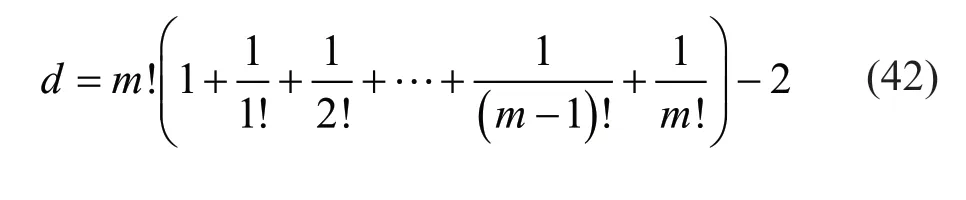
wheredis the total number of operations.By applying the method presented here for decoupling the equations and consideringnplates withksample points for each,it is required to calculate thendeterminant of the orderk,in which the total operations can be obtained by applying Eq.(42).However,considering all plates simultaneously,one (n×k)×(n×k) determinant should be obtained.Ifd1is assumed as the number of the required operations for the case of decoupling equations andd2for the coupled,it is obvious thatd2is considerably larger thand1,with the ratio of aboutd2/d1=(n×k)!/(n×k!).Also,if one applies LU decomposition or the Bareiss algorithm,the elementary operations for anm×mdeterminant are of O(m3) (Shores,2018).That is,the number of operations for the coupled equations is aboutn2larger than that for the decoupled ones (i.e.,(n×k)3/(n×k3)=n2).For example,if one considers a triple plate system,i.e.,n=3,and applies LU decomposition or the Bareiss algorithm,the number of the required operations for decoupled equations will be about one-ninth of the coupled ones,thereby revealing the computational efficiency of the method introduced in this article.

3 Results and discussions

As a case study for multiple plate systems,a triple plate system is considered with no connection to the ground (i.e.,k1=0 in Eq.(1)),Fig.3,in which all plates have the same geometry and material properties.A triple plate system can be considered as a development for piezoelectric bimorph plate case studies that frequently have been assessed in the related literature.

Fig.3 Elastically connected triple rectangular plates

To validate the solution method and the precision of its results,rigid connections are considered between the plates (k2→∞ andk3→∞),which makes the triple plate system turn into a system with one plate,allowing a comparison of the frequencies with those presented by Leissa (1973): good agreement is observed therein,as displayed in Table 1.

As for the other case,consideringλ=2,= 0.005,I2=0 and= 1048.3,i=1,…,n,the obtained natural frequencies for elastically connected 3,5,and 7 plates with an SSSS boundary condition are compared with those presented by Stojanovićet al.(2015),as shown in Table 2.Excellent agreement is observed,and is therefore a validation of this study.In Table 2,is the dimensionless stiffness of the elastic medium between (i-1) th andith plates,defined as:

Although the similarity of boundary conditions for all plates is a restriction of the presented method,this situation can be arbitrary.Considering the mixed boundary conditions,a triple plate system is of concern as shown in another case,Fig.4,in which each plate is simply supported on half of one side and clamped in the other half.In Fig.4,ξandηare the lengths of the clamped and simply supported portions,respectively,in whichη=2ξ.Forλ= 1,= 0.005 and= 1000,the first six natural frequencies of the system are tabulated in Table 3 and compared with those obtained by utilizing the ABAQUS finite element software,with which good agreement is observed.The first six mode shapes of the system with those obtained by the ABAQUS software are compared in Fig.5.

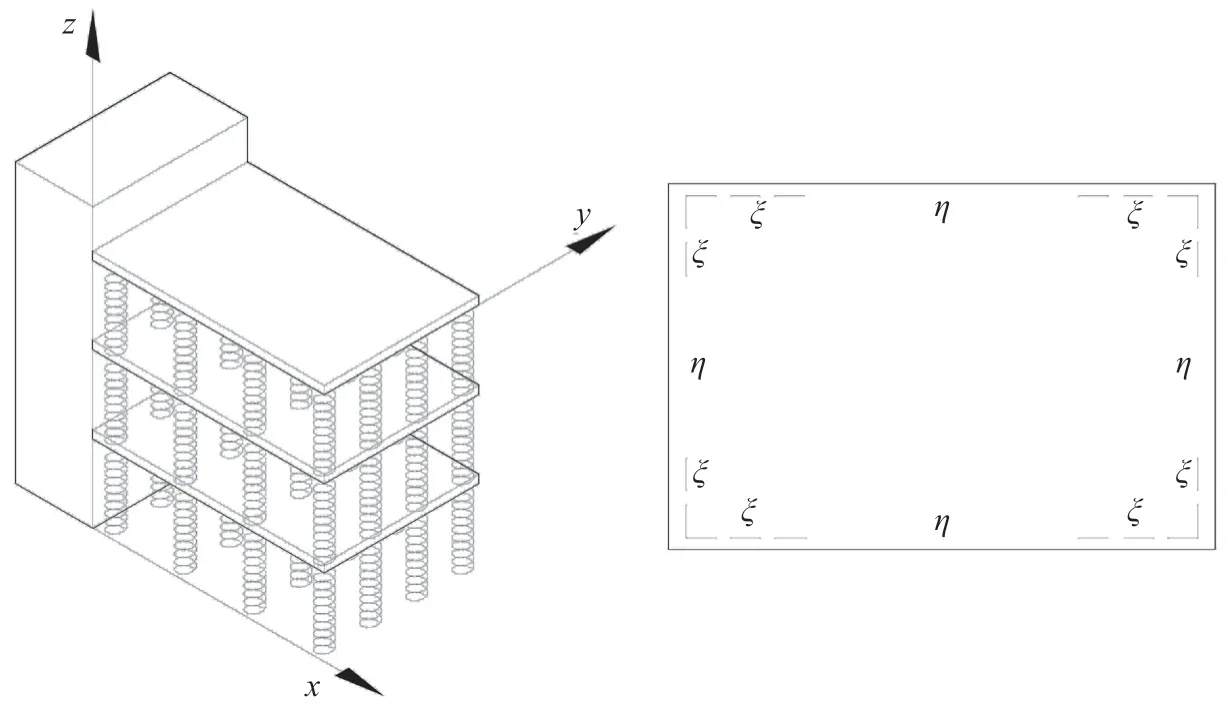
Fig.4 Triple plate system with mixed boundary conditions (ξ and η,the lengths of the clamped and simply supported portions,respectively)

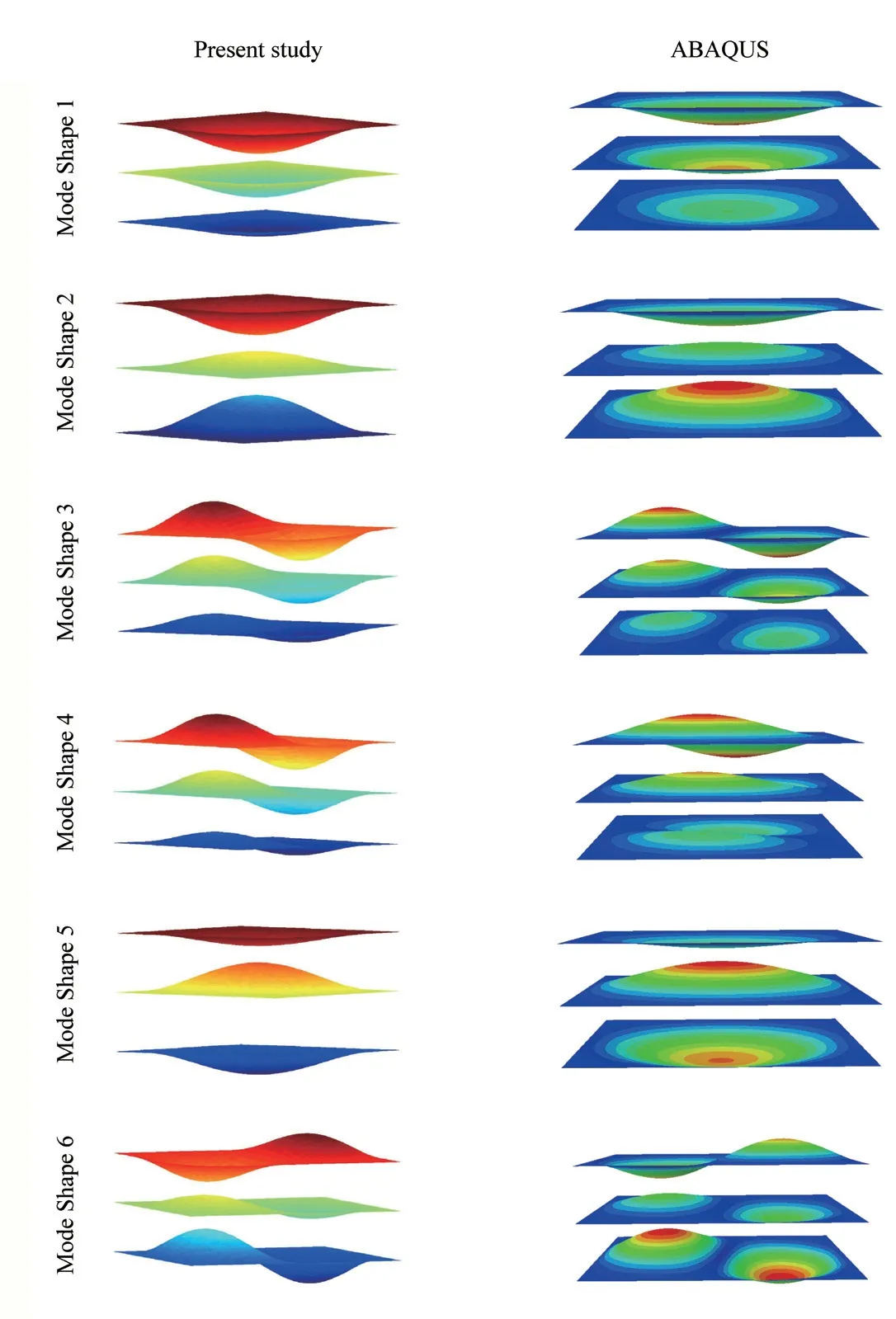
Fig.5 First six mode shapes of the triple plate system,with mixed boundary conditions (=1000,λ =1,=0.005)

According to Eq.(23),it is deduced that the vibrational behavior of the system is affected by the factors of geometry and the elastic properties of the connecting medium,represented by Winkler coefficients.The effect of geometry on the vibrational behavior of the system is briefed in the aspect ratio and the dimensionless thickness parameters,Eq.(23).Considering the triple plate system with no connection to the ground,as seen in Fig.3,the effect of these variables in the dimensionless frequencies is shown in Figs.6,7 and 8 for CFFF,CFCF and CCCC boundary conditions,respectively.As observed,the first and second dimensionless frequencies increase for CFFF boundary conditions by an increase in dimensionless thickness with a very small slope,unlike the aspect ratio,in which a decreasing effect is evident.The effect of the aspect ratio on the higherorder frequencies is completely different.In higherorder frequencies,after the third frequency an increase in the aspect ratio would increase dimensionless natural frequencies,as pictured in Fig.6.For a system with CFCF and CCCC boundary conditions,the dimensionless thickness has a small decreasing effect on dimensionless frequencies,as seen in Figs.7 and 8,respectively.For special values ofλand,considering Eq.(23) reveals the dimensionless natural frequencyΩpthat is only affected by the dimensionless thickness,due to terms.These terms are even neglected in some references due to the slight effects on thin plates (Rao,2007),leading to the slight effect ofthe dimensionless thickness on dimensionless natural frequencies,as shown in Figs.6-8.Despite CFFF boundary conditions,all natural frequencies of a system with CCCC boundary conditions increase with a rise in the aspect ratio,Fig.8.This increase is observed for a system with CFCF boundary conditions except for the first three natural frequencies,in which decreasing the natural frequencies is observed by an increase in the aspect ratio,as shown in Fig.7.Some numerical results for the first ten dimensionless natural frequencies are tabulated in Tables 4,5,and 6 for CFFF,CFCF,and CCCC boundary conditions,respectively.

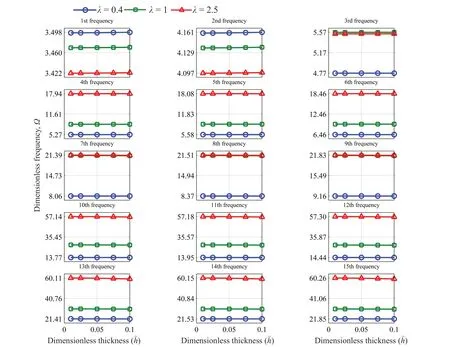
Fig.6 The effect of dimensionless thickness and aspect ratio on dimensionless natural frequencies (=4,=8,CFFF)

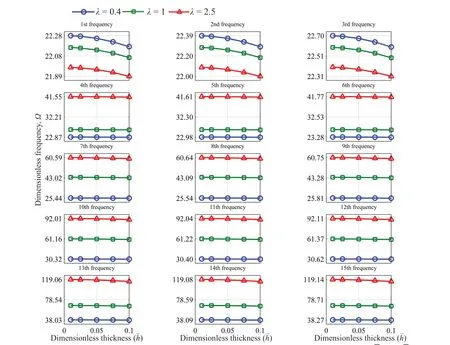
Fig.7 The effect of dimensionless thickness and aspect ratio on dimensionless natural frequencies (=4,=8,CFCF)

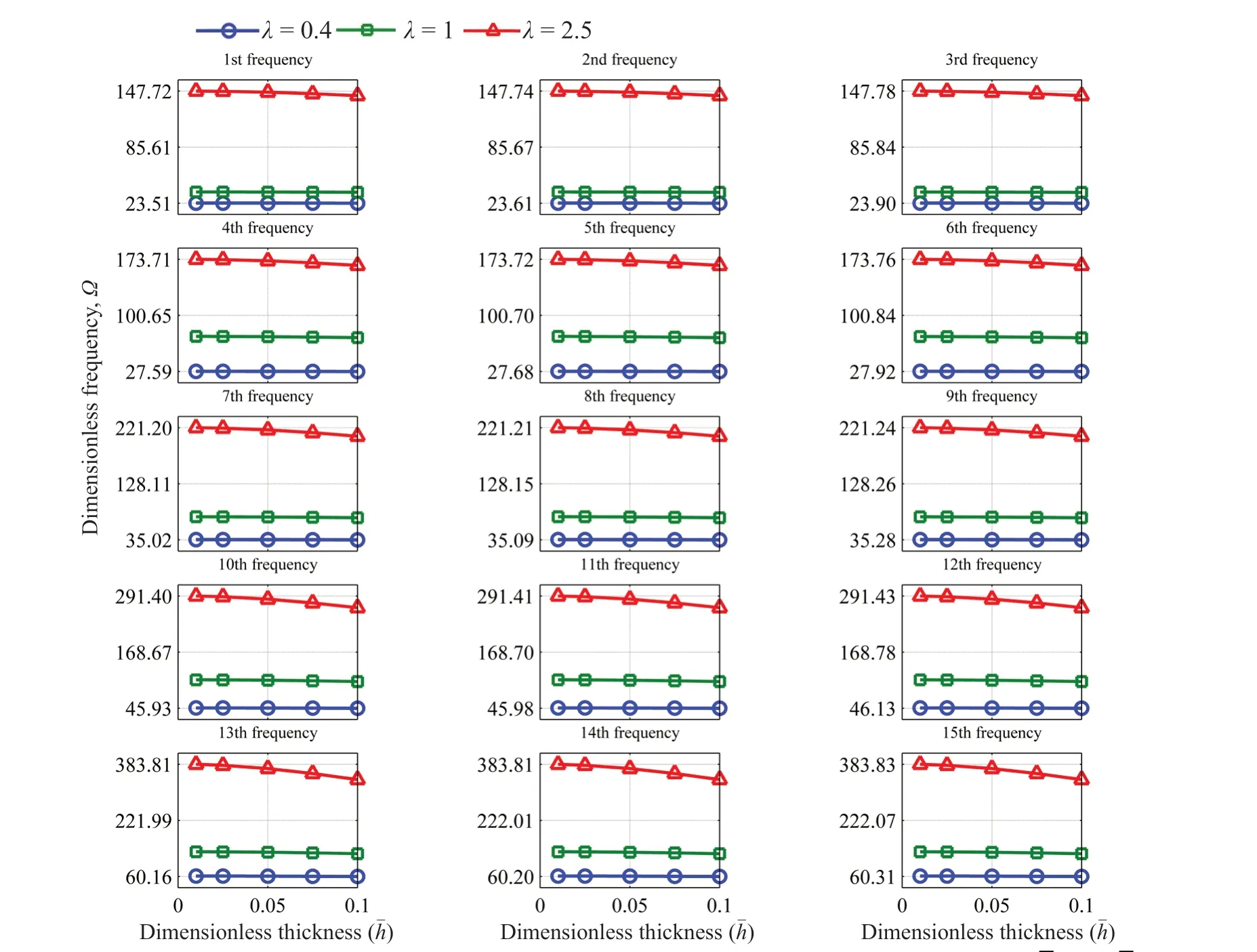
Fig.8 The effect of dimensionless thickness and aspect ratio on dimensionless natural frequencies (=4,=8,CCCC)

Table 1 Comparison of dimensionless natural frequencies for CFFF boundary conditions(k2 ,k3 ,=1,=0.1)

Table 1 Comparison of dimensionless natural frequencies for CFFF boundary conditions(k2 ,k3 ,=1,=0.1)

Table 2 Comparison of natural frequencies (s-1) for SSSS boundary conditions (=1048.3,=2,=0.005,I2=0)

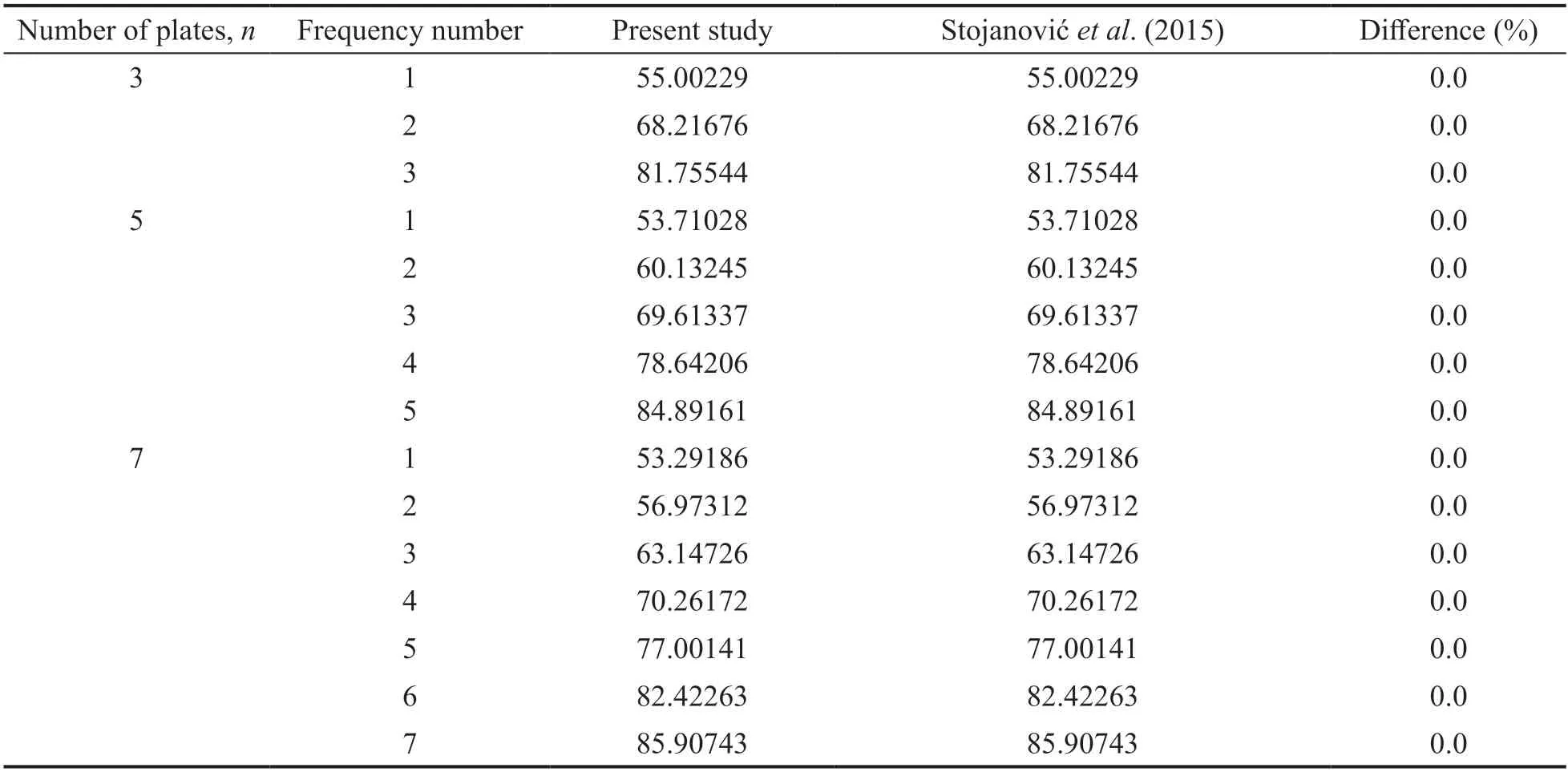
Table 2 Comparison of natural frequencies (s-1) for SSSS boundary conditions (=1048.3,=2,=0.005,I2=0)

Table 3 The first six natural frequencies (s-1) of the triple plate system,with mixed boundary conditions(=1000,λ =1,=0.005)

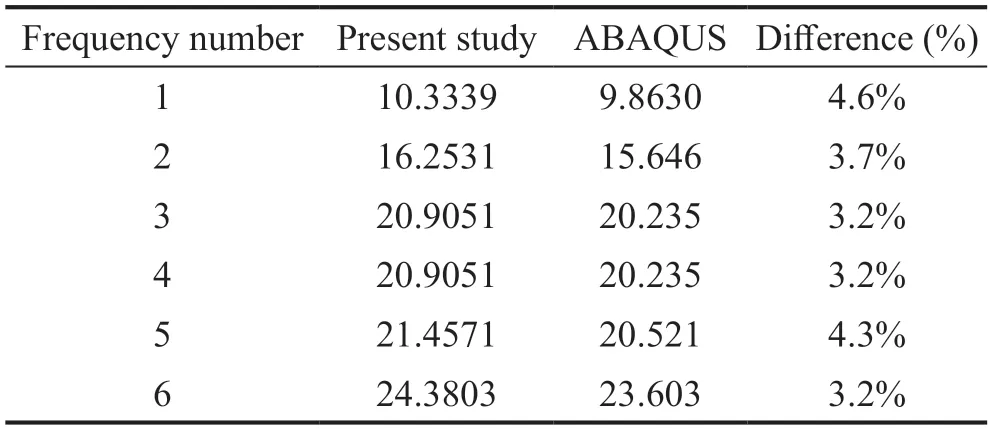
Table 3 The first six natural frequencies (s-1) of the triple plate system,with mixed boundary conditions(=1000,λ =1,=0.005)

The effects of stiffness coefficients are inquired on in the first fifteen frequencies,as shown in Figs.9,10 and 11 for CFFF,CFCF and CCCC boundary conditions,respectively.As anticipated,an increase in the dimensionless frequencies by increasing the stiffness of elastic connections for most frequencies is more evident;that is,increasing stiffness does not affect all frequencies,but does modify most.On the contrary,with no connection to the ground,the 1st,4th,7th,10th,and 13th dimensionless natural frequencies remain constant,which is due to the identical deflection shape of the similar plates in the corresponding modes,which inactivates the intermediate elastic layers (Ghafarian,and Ariaei,2016).The first ten dimensionless natural frequencies for different values of stiffness coefficients are tabulated in Tables 7,8 and 9 for CFFF,CFCF and CCCC boundary conditions,respectively.Thenatural frequencies of a system with CCCC boundary conditions exceed those of ones with other boundary conditions followed by CFCF and CFFF plate systems,respectively.This is due to the higher rigidity of a system with clamp boundary conditions,compared to a system with free ones on the same sides.Decreasing the effects of stiffness coefficients in higher-order modes occurs due to an increase in system rigidity.

Table 4 The effect of the aspect ratio and dimensionless thickness on the first ten dimensionless natural frequencies(=4,=8,CFFF)

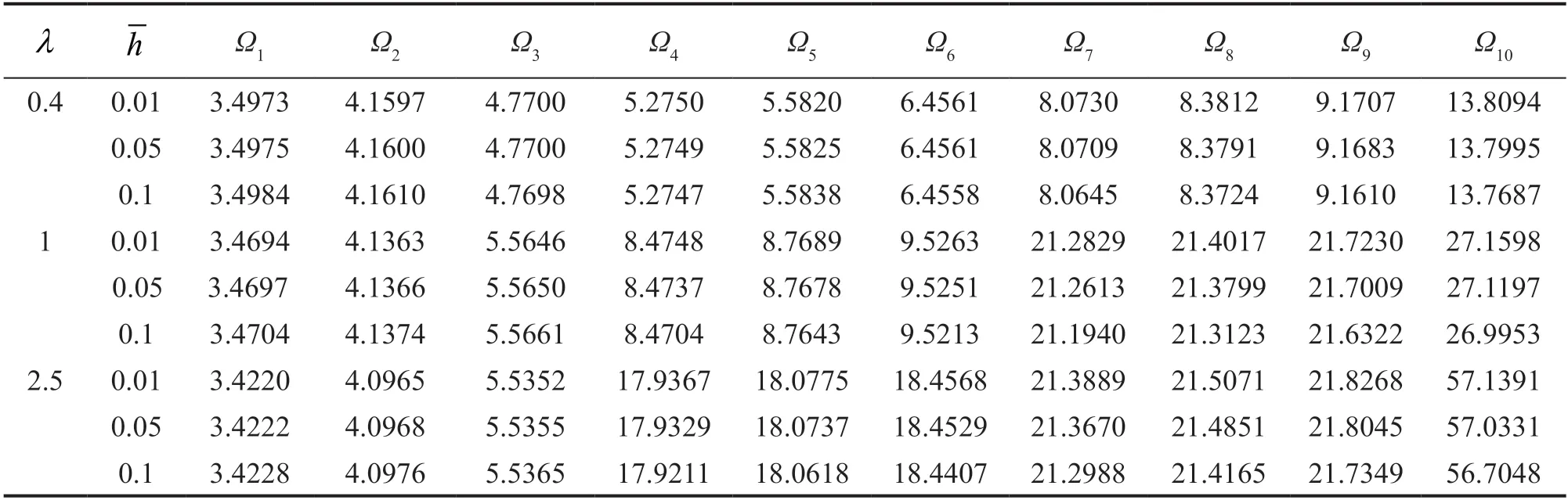
Table 4 The effect of the aspect ratio and dimensionless thickness on the first ten dimensionless natural frequencies(=4,=8,CFFF)

Table 5 The effect of the aspect ratio and dimensionless thickness on the first ten dimensionless natural frequencies(=4 =8,CFCF),

Table 5 The effect of the aspect ratio and dimensionless thickness on the first ten dimensionless natural frequencies(=4 =8,CFCF),

Table 6 The effect of the aspect ratio and dimensionless thickness on the first ten dimensionless natural frequencies=4 =8,CCCC)(,

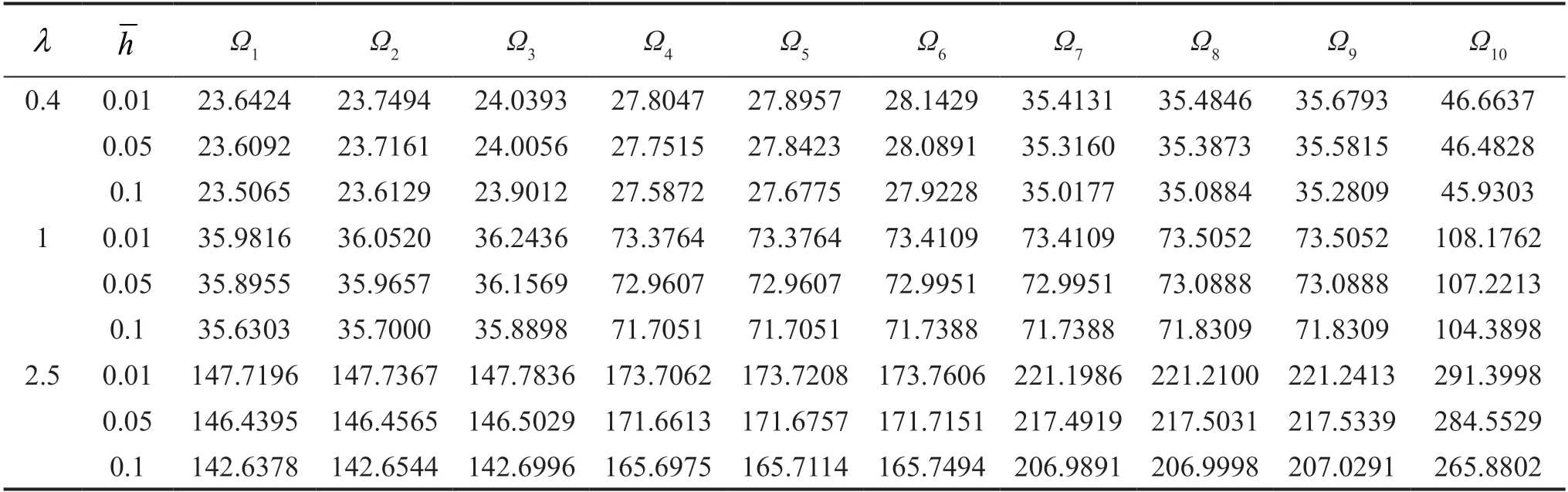
Table 6 The effect of the aspect ratio and dimensionless thickness on the first ten dimensionless natural frequencies=4 =8,CCCC)(,

Table 7 The effect of stiffness coefficients on the first ten dimensionless natural frequencies (=1,k2 =k ,k3=2k,CFFF)

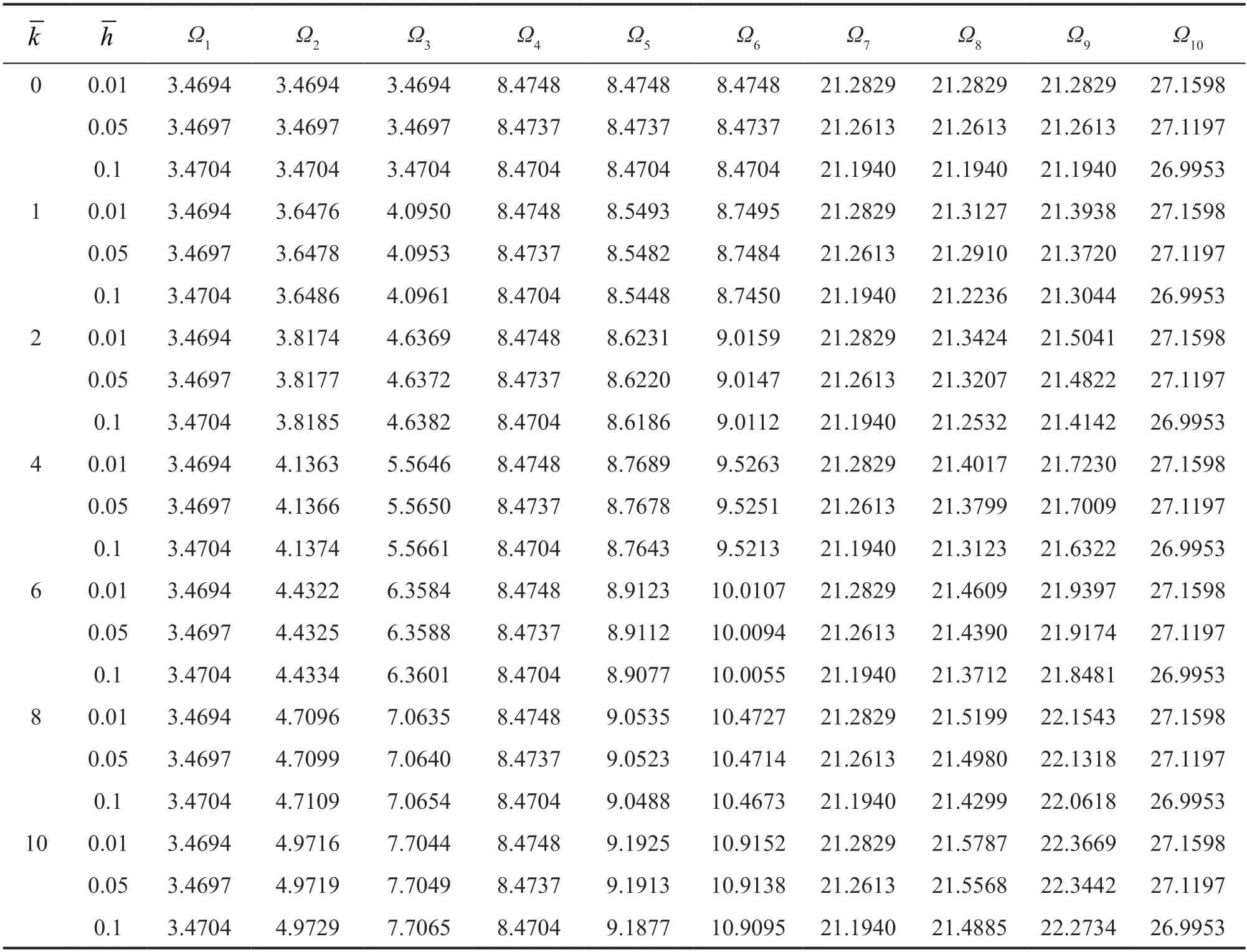
Table 7 The effect of stiffness coefficients on the first ten dimensionless natural frequencies (=1,k2 =k ,k3=2k,CFFF)

Table 8 The effect of stiffness coefficients on the first ten dimensionless natural frequencies (=1,= ,=,CFCF)

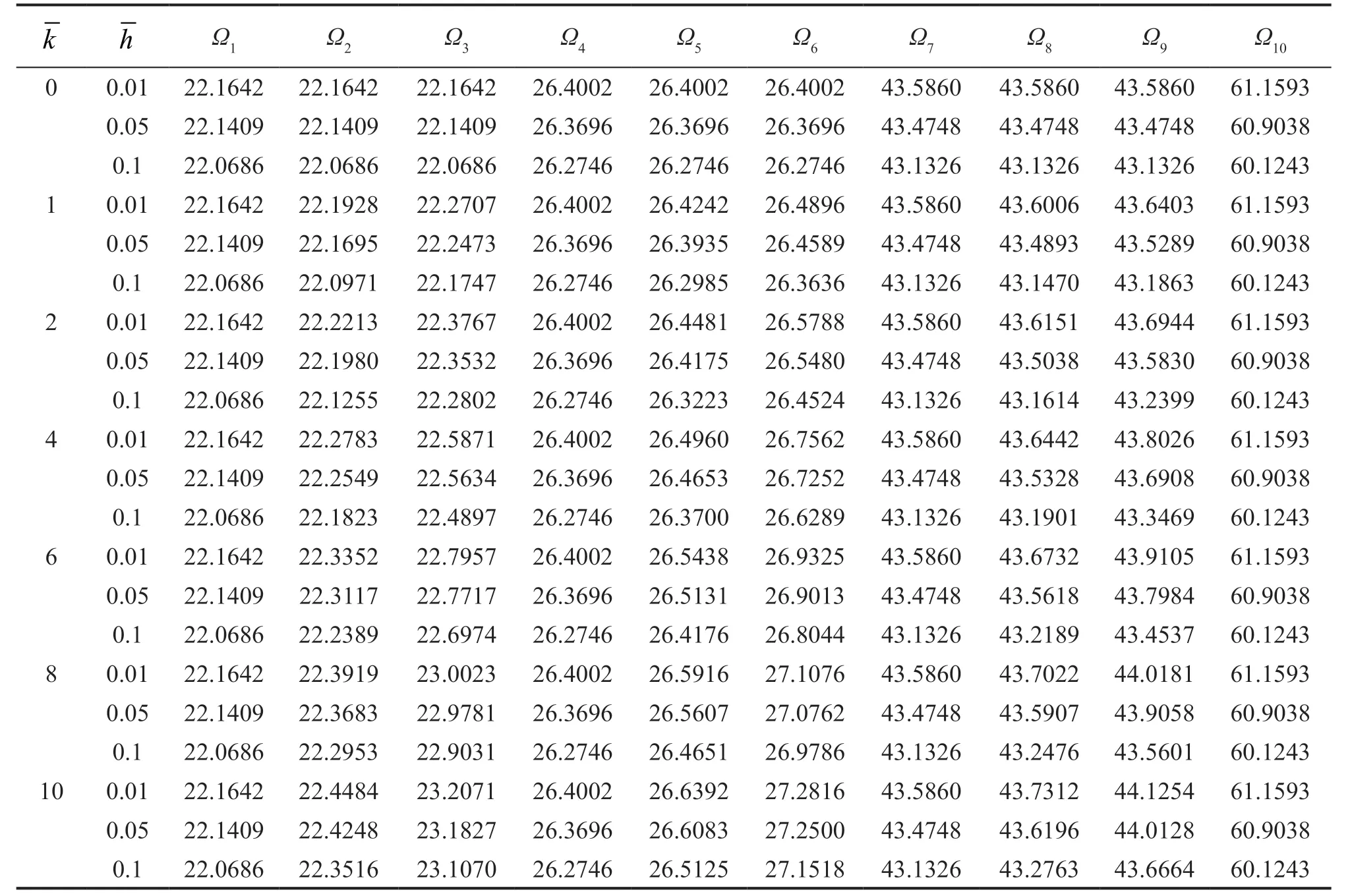
Table 8 The effect of stiffness coefficients on the first ten dimensionless natural frequencies (=1,= ,=,CFCF)

Table 9 The effect of stiffness coefficients on the first ten dimensionless natural frequencies (λ=1,= ,=,CCCC)

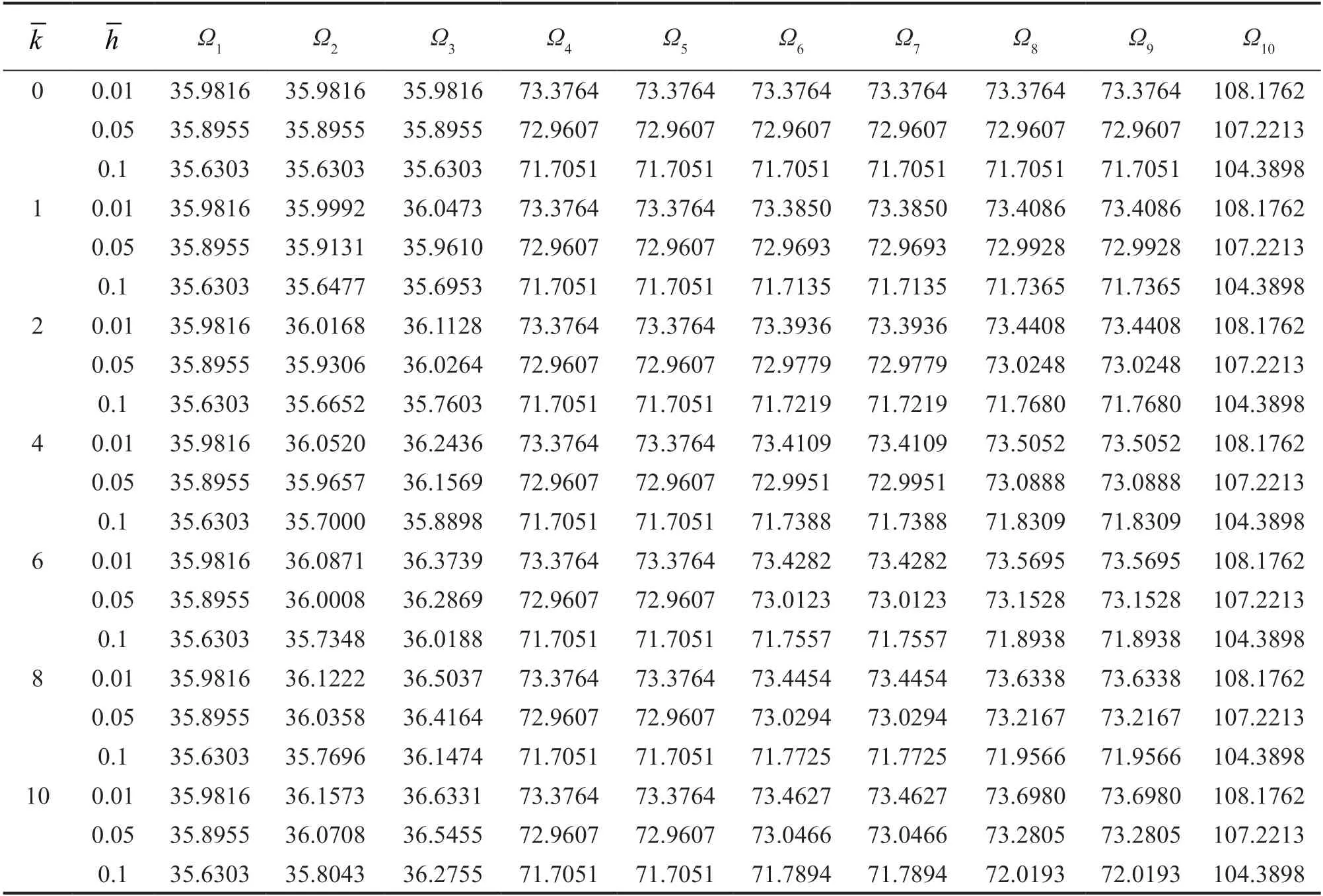
Table 9 The effect of stiffness coefficients on the first ten dimensionless natural frequencies (λ=1,= ,=,CCCC)

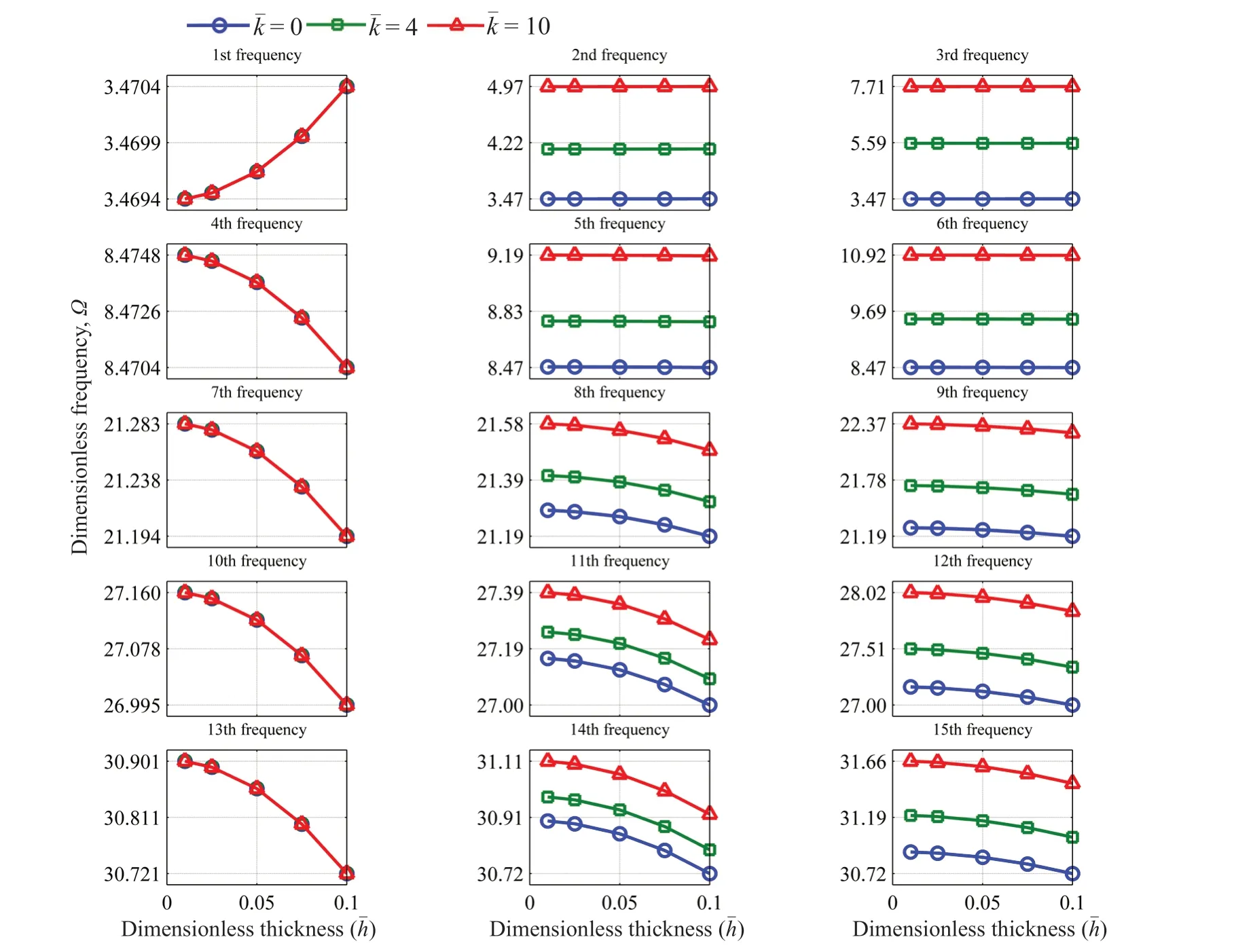
Fig.9 The effect of stiffness of elastic layers on dimensionless frequencies (=1, = ,=,CFFF)

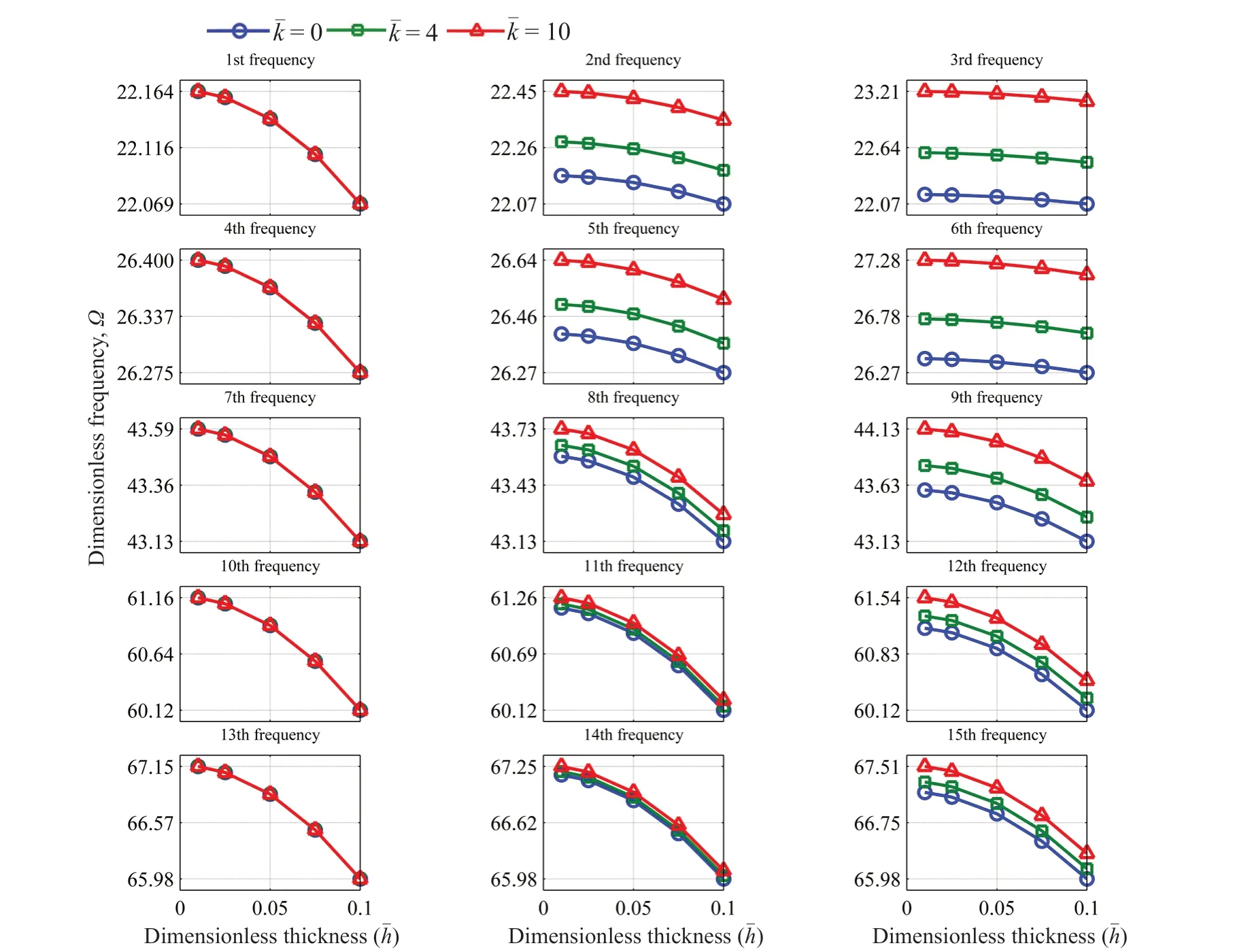
Fig.10 The effect of stiffness of elastic layers on dimensionless frequencies (=1,= ,=,CFCF)

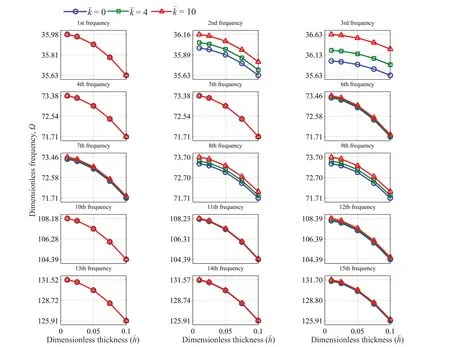
Fig.11 The effect of stiffness of elastic layers on dimensionless frequencies (=1,= ,=,CCCC)

The stiffness ratio effect on dimensionless frequencies is observed in Fig.12.The natural frequencies related to modes with the same pattern of plates are not influenced by the ratio between the stiffness coefficients;otherwise,the natural frequencies increase by a rise ink3.That considering a triple plates system leads to new natural frequencies in the vicinity of natural frequencies of a single plate may present the stiffness ratio as a parameter that could adjust frequencies for some applications such as mechanical energy harvesters (Malaji and Ali,2017).

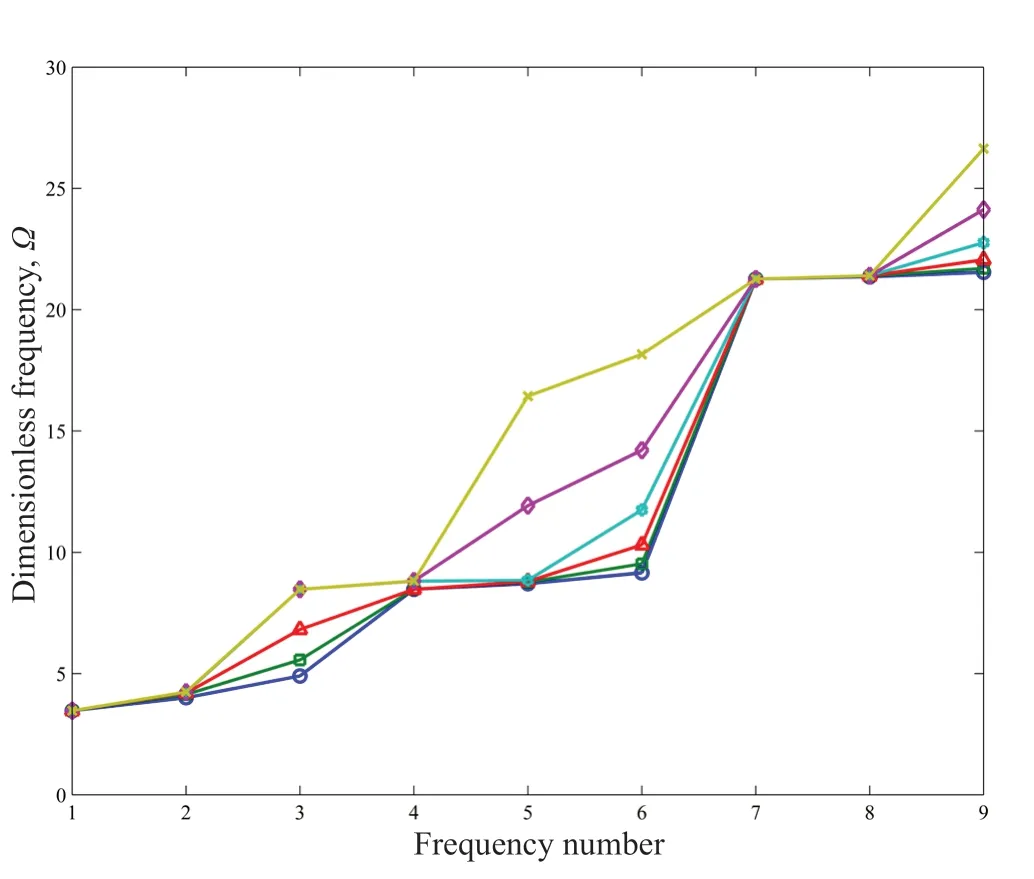
Fig.12 The effect of the stiffness ratio on dimensionless frequencies (CFFF,=1,=0.05, = 4);=4(circle),=8 (square),=16 (triangle),=32(hexagram),=64 (diamond),=128 (cross)

The first and the second frequencies of the plates in the decoupled system constitute the first six frequencies of the original system (Ghafarian and Ariaei,2016).The effect of stiffness coefficients on these frequencies is shown in Fig.13.The plates are identical,thus,atk=0,the first frequencies of all plates and the second ones coincide,as shown in Fig.13.As already known,an increase in stiffness coefficients does not affect the first and fourth frequencies due to the similar deflection shape of the plates in the corresponding modes,as shown in Fig.14,in which the first six modes are illustrated.

Fig.13 The effect of stiffness coefficients on the first two frequencies of the decoupled plates(=1,=0.1,= ,=): the decoupled plates′ first frequencies (solid-line),the decoupled plates′ second frequencies (dash-line);Plate 1 (blue circle),Plate 2 (green square),and Plate 3 (red triangle)

Fig.14 First six mode shapes of the system (=1,=0.1,=4,=8)

4 Conclusion

The free vibration of an elastically connected multiple plates system is assessed by assuming Kirchhoff′s plate theory.Due to difficulties in solving the coupled differential equations,a new change in variables is presented to allow the uncoupling of the equations and to obtain free vibration characteristics by applying the solution methods available for a single plate (such as the differential quadrature method) by means of a reduced computational effort.The two restrictions on this method are (1) the plates must be identical,and (2) the boundary conditions on the same side must be the same,although they can be arbitrary.By assessing the influence of many parameters,the following results are observed:

· As expected,an increase in stiffness coefficients acts to increase most frequencies,while with no connection to the ground due to the similar deflection shape of identical plates in corresponding modes,this does not occur.These frequencies are the same as those of a single plate system.

· The effect of stiffness coefficients in higherorder modes decreases due to an increase in system rigidity.

· The natural frequencies of a system with CFFF boundary conditions,because of the lesser rigidity of the free boundary condition compared to the clamp one,are lower than those of the CFCF and CCCC.

· With no elastic connections,the original and decoupled systems are the same;thus,the natural frequencies of all three plates coincide.

· In a system with thin plates,the effect of the dimensionless thickness on dimensionless natural frequencies is slight.

· Both the first and second frequencies of a system with CFFF boundary conditions and the first three frequencies for a system with CFCF boundary conditions decrease with an increase in the aspect ratio,while in the case presented here,the effect of the aspect ratio on higher-order frequencies is opposite.All frequencies of a system with CCCC boundary conditions increase,with a rise in the aspect ratio.

This approach can be applied in a system with an arbitrary number of plates with the feature to be modified by considering the various types of mechanical systems,such as parallel membranes and shells.

Acknowledgment

The authors would like to thank the Iran National Science Foundation (INSF) (Grant No.97021731).