基于三维建模和有限元分析的泥浆泵曲轴疲劳寿命评估
2022-10-19潘志杰张利贤
陈 艳,潘志杰,张利贤
(1.陕西机电职业技术学院智能制造学院,陕西 宝鸡 721001)(2.宝鸡石油机械有限责任公司,陕西 宝鸡 721002)
泥浆泵是石油勘探钻井作业的主要工具之一[1],随着石油勘探与钻井深度的不断增加,对泥浆泵的结构设计提出了更高要求,如泥浆泵曲轴要满足轻量化、大功率、低波动性等基本需求[2-3]。此外,高强度钻井作业还要求泥浆泵曲轴等主要零部件具有更高的刚度、可靠性、抗疲劳性及更长的使用寿命。曲轴是泥浆泵最重要的零部件,如果在使用过程中曲轴逼近最大负荷,将显著增加曲轴发生断裂的风险,同时影响泥浆泵的可靠性和使用寿命[4]。泥浆泵工作时,钻井的交变载荷会对曲轴产生巨大的扭矩与金属应力[5],如果能够对泥浆泵曲轴的工作状态、疲劳程度和使用寿命做出合理监控与评估,就可以有效避免由于泥浆泵曲轴断裂或其他突发故障给勘探钻井工作带来巨大损失。目前,针对泥浆泵曲轴疲劳度和寿命的评估,较为常用的方法主要有实验评估法[6]和金属磁记忆(metal magnetic memory,MMM)评估法[7]。其中实验评估法是在实验室环境下,利用伺服液压系统检测泥浆泵曲轴的剩余寿命。虽然依靠实验室检测能够评估出曲轴的疲劳度和剩余寿命,但该方法的评估成本较高,评估过程繁琐,实用性不强。MMM评估法是一种无损的曲轴寿命评估方法,基于泥浆泵的工作载荷和漏磁场应力集中情况[8],检测和判断曲轴是否存在金属疲劳或表面裂纹等情况。为了提高有限元模型的工作效率、直观性和计算精度,以便更准确评估出泥浆泵曲轴的金属疲劳程度和剩余使用寿命,本文利用三维建模的方式对传统有限元模型进行了优化。
1 泥浆泵曲轴运动规律与受力分析
泥浆泵曲轴由于金属疲劳产生损伤是一个累积的过程,随着曲轴服役时间的增加,其承受的动应力值就会逐渐接近甚至大于金属材料的疲劳限值[9]。如果曲轴的寿命为固定值N,经过n个周期变化给曲轴造成的累计损伤值为n/N。经过若干个周期后曲轴内部应力损伤会达到一个临界阈值χ,超过阈值金属就会发生断裂等损伤。
(1)
式中:ni为第i个周期;Ni为与ni相对应的应力级数。
泥浆泵工作时,曲轴的曲柄连杆运动过程如图1所示。

图1 曲柄连杆运动过程
图中AB为曲柄连杆,长度为L,C为曲柄连杆的质心,AB=4AC,OA的长度是连杆运动过程中,以曲轴右侧作为运动正方向而产生的距离,用D来表示。曲柄连杆柱塞十字头运动位移s、运动速度v和运动加速度a的计算公式如下:
(2)
式中:α为OA与x轴的夹角,其角度值随着曲柄连杆的移动而变化;ω为OA运动中的相位值,ω=α/t,其中t是曲柄连杆运动周期。曲轴运动时曲柄连杆做连续刚体平面运动,AB与x轴的摆角为β,α与β的角度变化关系决定了曲柄连杆的位置:
sinβ=Dsinα
(3)
泥浆泵曲轴受到连杆剪力F1、偏心惯性力F2、支撑座反力F3和主轴承座反力F4的影响。泥浆泵曲轴通常包括3~5个曲柄连杆,设第1个曲拐相位为φ1,在一个五曲柄连杆系统中,第i个曲拐的相位φi表示为:
(4)
曲轴所受连杆的剪力F1会随着曲拐相位的变化呈现周期性的变动,容易造成金属疲劳。由于曲拐偏心质量的存在会给泥浆泵曲轴带来向外的离心力,第i个曲拐偏心质量惯性力F2i表示为:
F2i=Lω2msinαj
(5)
式中:αj为第j个时刻OA与x轴的夹角;m为曲轴质量。支撑座反力F3和主轴承座反力F4会在一定程度上相互抵消,对曲轴金属疲劳度的影响程度,与偏心惯性力和连杆剪力相比较小。
2 泥浆泵曲轴三维建模有限元分析
针对曲轴几何结构进行三维建模,识别出载荷相对集中的区域做重点检测,并进行有限元分析,可以减少数据的采集量和检验量,降低检测评估成本。三维建模过程中利用激光设备采集曲轴的点云集合,对重点部位加大点云采集密度,划分出更密集的有限元网格。泥浆泵曲轴的主轴颈、曲柄连接处和曲柄连杆的轴径处承受的压力最大,在采集点云集合和划分网格时应提高节点的密度,可以将其设定为点云密度的最低值2 mm。三维点云集合的构建和网格的划分,为有限元模型的建立提供了基础框架,利用点云集合能够对泥浆泵的曲轴实施三维离散化处理。
有限元单元的载荷量τe与单元刚度ζe及节点位移量de之间的关系如下:
τe=de×ζe
(6)
节点位移向量与单元的应变向量相关,关联关系如下所示:
(7)
式中:ε为应变向量;G为与之相对应的几何矩阵。为确定载荷量和整体位移量,将离散化处理后的单元重新组合做整体分析,如果离散单元包括M个位移量,按照三维建模网格节点序号重新排列位移,位移量de表示为:
de=[d1,d2,d3,…,di,…,dM]T
(8)
式中:dM为离散单元位移量。
通过整体分析得到各单元内部的载荷量、节点位移变化情况和金属应力情况。曲轴所承受的应力主要由曲柄连杆的作用力所决定,计算曲轴截面所承受应力时需要在曲拐处建立动坐标系Ox0y0z0,曲轴和动坐标系以相同的角速度υ转动,动坐标系与原有的静坐标系Oxyz的转化过程如图2所示。

图2 动静坐标系转换过程
动坐标系在移动过程中z0轴与静坐标系保持重合,x0轴向和y0轴向分别与曲柄连杆径向分量和切向分量平行。动坐标系开始旋转时,x0轴(或y0轴)与静坐标系x轴(或y轴)的夹角为α′,动坐标系和静坐标系的转换关系如下:
(9)
利用动静坐标转换、外力的计算可以推算出曲轴各界面所承受的内部应力,计算中为了提高效率、降低复杂度,应优先计算三维建模网络密集的区域,以便大致判断出应力集中的区域,并选取具有代表性的界面。然后利用软件编程方法或MATLAB仿真方法计算曲轴应力较大界面的扭矩和弯矩。
3 泥浆泵曲轴疲劳寿命评估
利用三维点云集合和有限元模型,能够识别出曲轴和曲柄所受的应力情况,再基于有限元模型分析曲轴的金属疲劳情况,具体步骤包括曲轴金属疲劳强度的评估和曲轴全周期疲劳寿命的评估等。通常情况下,制造泥浆泵曲轴采用的材料是泊松比为0.29的高强度31CrMoV9,该材料的强度极限σu和疲劳极限σf之间的关系如图3所示。

图3 曲轴金属强度极限和疲劳极限之间的关系
通过大量的实验描点绘制出强度极限σu和疲劳极限σf之间的关系曲线(OA和AB),当强度极限达到1 500 MPa左右时,31CrMoV9出现金属疲劳,容易发生断裂。曲轴除了受到应力的影响之外,如果金属表面存在缺陷也容易导致曲轴断裂。以曲轴承受的应力集中系数κ1和曲轴表面加工系数κ2为基础,可以计算出曲轴疲劳综合影响系数,κ1和κ2之间的关系如下:
κ1=1+ζ(κ2-1)
(10)
式中:ζ为高强度31CrMoV9材料的敏感系数。那么曲轴综合疲劳影响系数κt可以表示为:
(11)
式中:η1为金属表面综合影响系数;η2为曲轴的强化系数。通常情况下,曲轴发生断裂时金属表面综合影响系数会达到峰值。
将泥浆泵曲轴受到的曲柄杆剪力、偏心惯性力、动静坐标系转换值、金属疲劳综合影响系数等参数值输入有限元模型,就可以综合评估曲轴的疲劳寿命与损伤程度。
4 实验部分
4.1 实验参数设置
在实验室环境下,对一个已经退役但并未损坏的4缸单作用泥浆泵曲轴进行测试评估实验,曲轴实物如图4所示。

图4 实验用泥浆泵曲轴实物图
待检测的曲轴表面有锈蚀、油污,需要先做必要的清理和去污,并采用涡流探伤确保该实验用曲轴表面不存在出现裂纹和发生断裂的风险。
实验中,泥浆泵曲柄与连杆比值为1∶6.5,泥浆泵的额定功率为2 500 kW,最大工作压力为80 MPa。
4.2 数据分析
本文基于三维建模和有限元网格划分原理,重点对曲轴的主轴颈圆角和曲柄圆角进行扫查,并构建三维有限元模型。在泥浆泵曲轴的主轴颈和曲柄等应力集中的区域分别选取5个测试点,计算和评估曲轴的损伤值,为的是评估结果更为直观,同时引入文献[6]和文献[7]评估方法参与对比。基于三维建模有限元方法的测试结果见表1。

表1 有限元模型疲劳度计算结果

续表
文献[6]和文献[7]两种传统曲轴疲劳度评估方法的计算结果,见表2和表3。
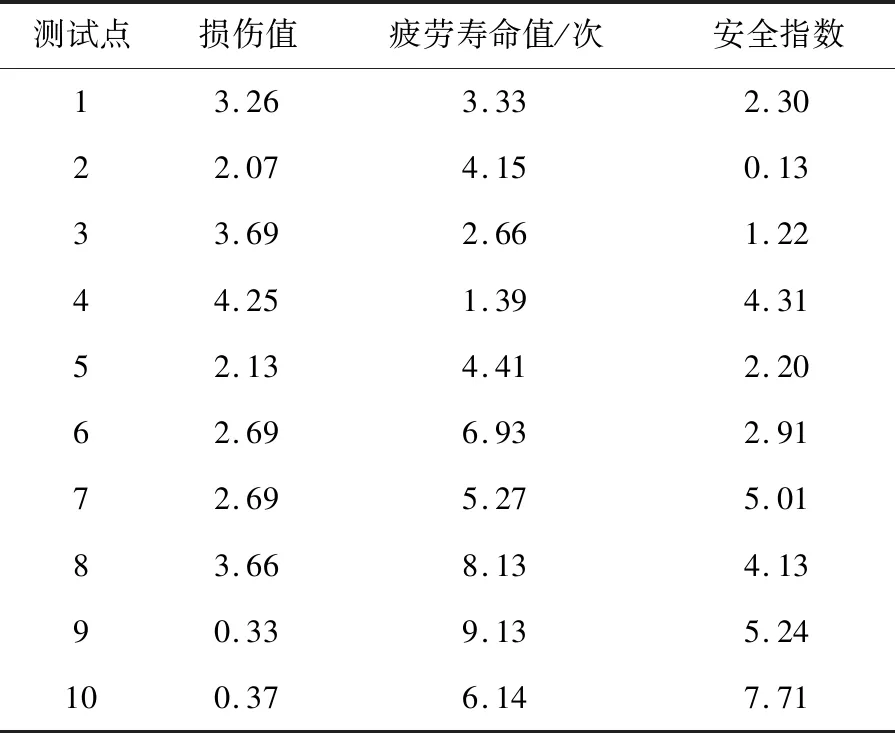
表2 文献[6]评估方法疲劳度计算结果
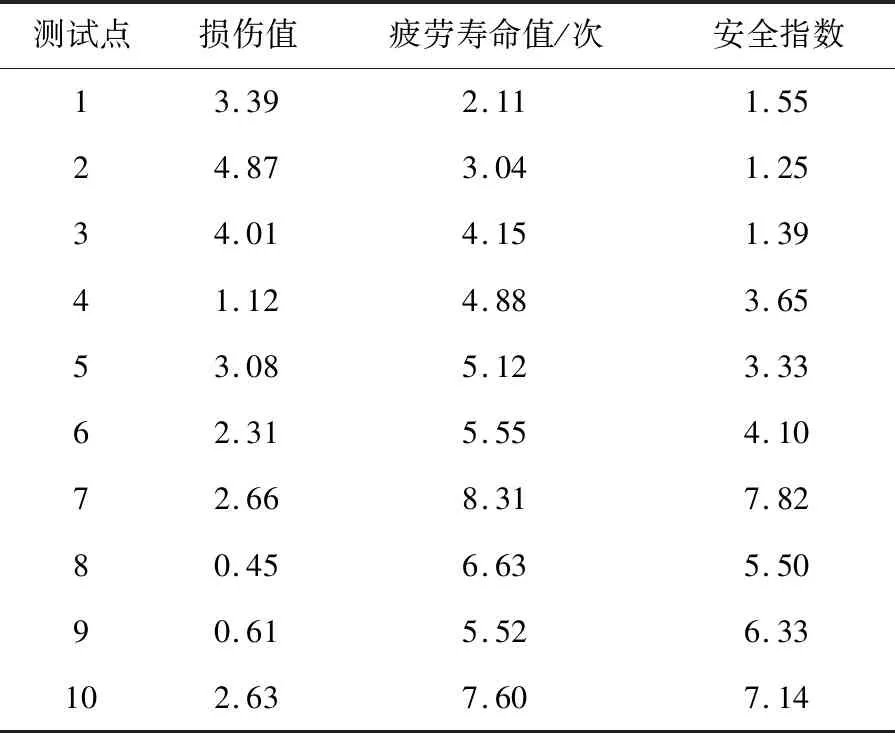
表3 文献[7]评估方法疲劳度计算结果
按照实验用泥浆泵曲轴的理论使用寿命,继续在实验室条件下模拟曲轴工况,并实时观测曲轴主轴颈和曲柄应力变化情况,当曲轴工作时间趋近于其理论使用寿命,但尚未出现损坏时,对曲轴的10个测试采样点损伤值进行实地测量,并与评估数据对比,数据对比结果如图5所示。

图5 评估结果验证
由图可知,本文方法的评估结果与理论值最为接近,证明该方法具有良好的评估准确性;而文献[6]和文献[7]的评估结果与理论值相比具有较大的差距。当疲劳测试完毕后,检测了主轴颈圆角实际的磁场强度梯度均值和曲柄圆角实际的磁场强度梯度均值,并与有限元模型的梯度值进行对比,结果如图6所示。圆角是曲轴的结构,分别从每个圆角处取2个测试点。

图6 主轴颈圆角磁场强度梯度均值数据统计
实际测试结果显示,利用三维建模有限元模型对主轴颈扫描结果与理论值趋近,验证了本文提出的评估方法的有效性。
5 结束语
本文首先通过建模分析泥浆泵曲轴的受力变化情况和金属疲劳度,判断金属件内部是否存在裂纹,然后基于三维激光点云集合数据采集方法构建有限元网络模型,能够更准确地分析出泥浆泵曲轴内部的应力变化情况,从而更准确地评估主轴颈和曲柄的金属是否存在出现裂纹或内部损坏的风险。实验结果表明,通过对主轴颈和曲柄应力变化情况的数据分析,曲柄圆角实际的磁场强度梯度均值与理论值相近,表明本文提出的评估方法具有较好的评估准确性。
