旋转圆柱微间隙剪切流动特性研究

朱桂平,马兆坤,郭义盼,张镜洋

(南京航空航天大学航天学院，江苏 南京 210016)

动压气体轴承以气体作为润滑介质，具有转速高、摩擦力小、功耗低等诸多优点，因此广泛应用于压缩机、航空仪器等领域，且其也是微型燃气轮机的关键部件之一[1]。动压气体轴承在工作时，转轴与轴承套存在的偏心，使两者之间形成楔形通道，气体进入楔形通道产生压力梯度，从而形成支撑转子的承载力，这种现象被称为动压效应。为了产生较强的动压效应，轴承间隙尺度往往在200 μm以下，属于微尺度间隙，且转轴通常需要保持10 000 r/min以上的高速旋转。

对旋转圆柱微间隙剪切流动的研究，最早可以追溯到19世纪末，雷诺提出了著名的用于描述轴承微间隙压力分布的雷诺微分方程。此后Diprima等[2]通过研究发现，微小尺度下雷诺方程近似等于N-S方程，因此雷诺方程在滑动轴承研究中的应用得到了显著发展。例如，文献[3]、[4]通过推导求解出可压缩流体雷诺方程，分析了气体的压缩性以及边界滑移现象对间隙内的压力分布和承载力的影响。文献[5]、[6]将雷诺方程与能量方程耦合，计算出微间隙内的压力和温度分布，并分析了转速和载荷对温度分布等的影响。通过求解雷诺方程虽能获得大量气膜特性信息，但却难以反映间隙内部更为详细的流场信息，因此发展出了其他用于研究旋转圆柱微间隙剪切流动的方法,如有限元模型[7]可用来求解可压缩、黏性、稳态的N-S方程，并与能量方程进行耦合来研究热流体动力学现象。在有限体积法的应用上则着重研究了间隙大小、偏心率等对气膜速度和压力场的影响[1，8]。如Chun等[9]采用非结构化有限体积法模拟间隙流动，研究边界条件和偏心率对流场的影响。

动压气体轴承在工作时形成的间隙流动是一种典型的泰勒-库特流动。对于常规尺度的泰勒-库特流动，部分学者研究分析认为间隙内压力梯度、流体剪切力及离心力是泰勒涡产生的重要因素[10-11]。在泰勒-库特流动中，偏心也是必不可少的影响因素，在偏心状态下流动的稳定性往往小于同心时的稳定性[12]，并且偏心的增加有利于周向回流的出现[13]，进一步研究还发现，随着旋转雷诺数的增加，分离点沿旋转方向移动[14]。而在偏心条件下，随着偏心率的增大，泰勒涡的强度减小，最强的泰勒涡出现在最宽气隙下游的45°～90°范围内[15]。此外有学者研究发现，在泰勒-库特流基础上叠加轴向流动，间隙内泰勒涡产生的非线性行波和调制非线性波均产生相应的扰动变化[16]。针对微小尺度间隙，Deng等[17]研究了偏心率在0～0.8、间隙大小为0.01英寸的偏心圆柱体狭缝中流场，进一步验证了临界转速本身随着偏心率的增大而单调增加，且临界转速与偏心率呈函数关系。

综上所述，对于旋转圆柱微间隙剪切流动的研究，主要集中于对雷诺方程的求解，以及宏观压力场、温度场和承载力的研究，缺少对微间隙内流场特别是速度分布的描述，而在泰勒-库特流动的研究中，目前主要针对的是数倍于轴承间隙的较大尺度的研究，对于更小尺度下泰勒-库特流动的分析需要更进一步的探索。本文着眼于以气体为介质的旋转圆柱微间隙剪切流动，通过数值计算获得不同偏心率、转速和间隙比等工况下压力、速度分布规律和流动机理。同时对偏心下泰勒-库特流动进行分析，包括流动形态及泰勒涡对速度分布产生的影响。

1 模型与方法

旋转圆柱微间隙剪切流动中，流动间隙的轴向截面为偏心环状通道，由于偏心的存在，使得圆柱间出现楔形通道，从而产生动压效应，偏心环状间隙截面图如图1所示。

图1 偏心环状间隙截面图

其中内壁面为旋转壁面，半径为R1，其绕圆心O1以恒定的角速度ω转动；外壁面为静止壁面，半径为R2。偏心距e为内外壁面圆心O1与O2的距离。θ为该环状间隙的周向角，最大间隙高度位于θ=0处，最小间隙高度位于θ=π处。内外壁面半径之差为径向平均间隙C，因此间隙比δ可以表示为[18]：

(1)

偏心率ε可用偏心距e和平均间隙C的比值来表示：

(2)

雷诺数Re可由下式表示：

(3)

式中：υ为动力黏度，为运动黏度μ和流体密度ρ之比。周向角θ逆时针围绕圆心O1在0～2π间变化，因此间隙高度h可以表示为：

h=C(1+εcosθ)

(4)

旋转圆柱微间隙剪切流动也是偏心下的泰勒-库特流动，使用泰勒数来描述流动状态，当泰勒数达到临界值时间隙内出现泰勒涡流。泰勒数Ta可由下式表示[12]：

(5)

通过泰勒数Ta可计算转速n：

(6)

(7)

建立三维旋转圆柱微间隙剪切流动数值计算模型，两壁面均视为刚性壁面，且不考虑变形等影响。流场轴向端面设置为周期性边界条件，以忽略端部效应干扰。流场计算网格模型如图2所示，采用结构化网格划分流体域，并保证边界网格y+值在1左右。间隙内部流体设置为可压缩的理想气体，使用大涡模拟(large eddy simulation,LES)计算模型进行瞬态求解，残差值设置为10-5，同时在流场内创建监控点，监控每次迭代后的参数变化，以此判断计算是否达到收敛。为了验证网格无关性，分别对间隙高度上不同网格层数N进行计算，结果如图3所示，通过对比可知，在确保y+值在合理范围内条件下，网格数量变化不影响计算结果。

图2 流场计算网格模型

图3 网格无关性比较结果

在使用大涡模拟控制方程进行解算时，流速ui经过脉动过滤器可以分解为：

(8)

过滤后的N-S方程为：

(9)

(10)

(11)

在微间隙尺度下计算旋转圆柱微间隙剪切流动时需要考虑滑移边界条件。使用克努森数Kn判定滑移边界，Kn定义如下：

(12)

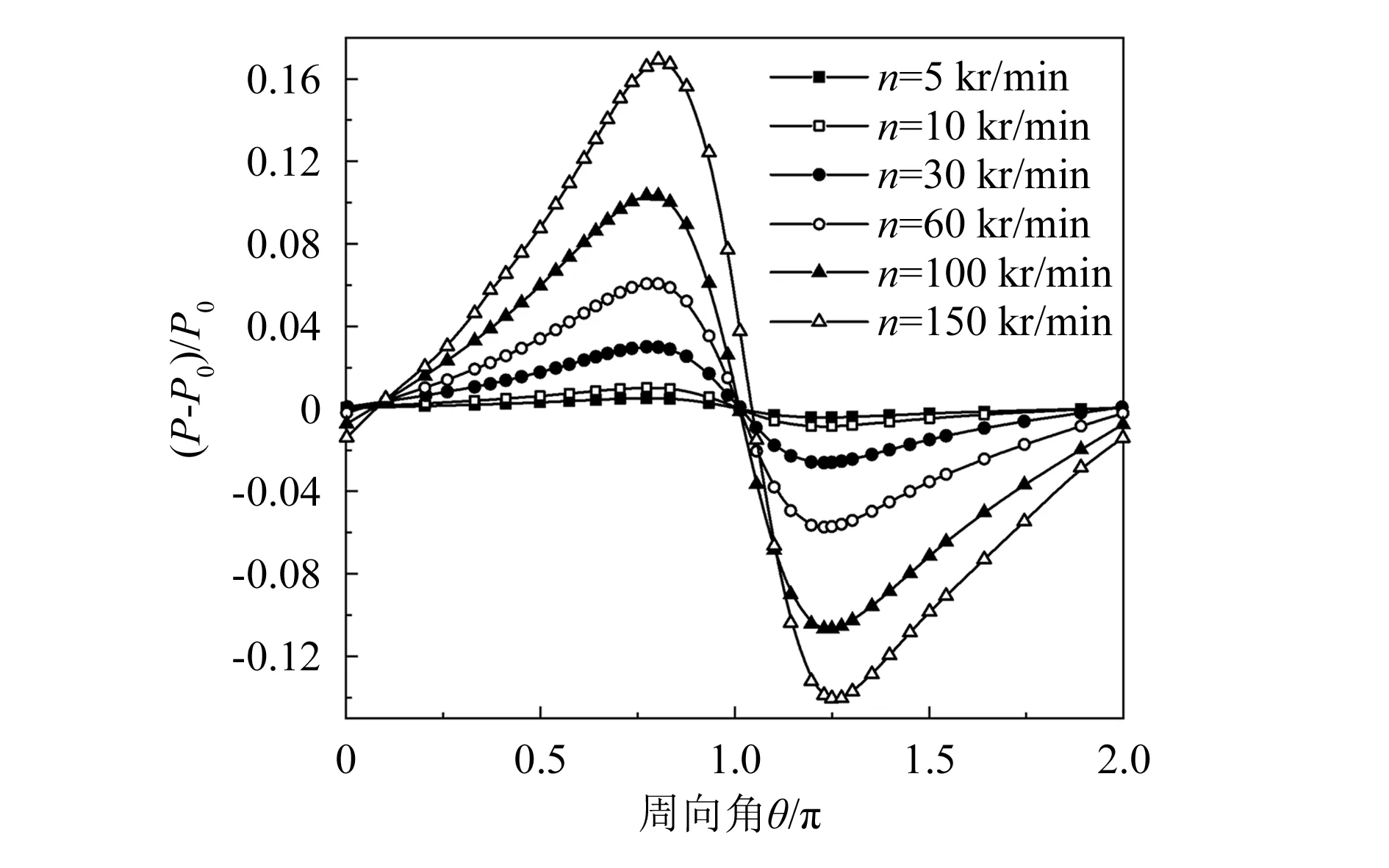
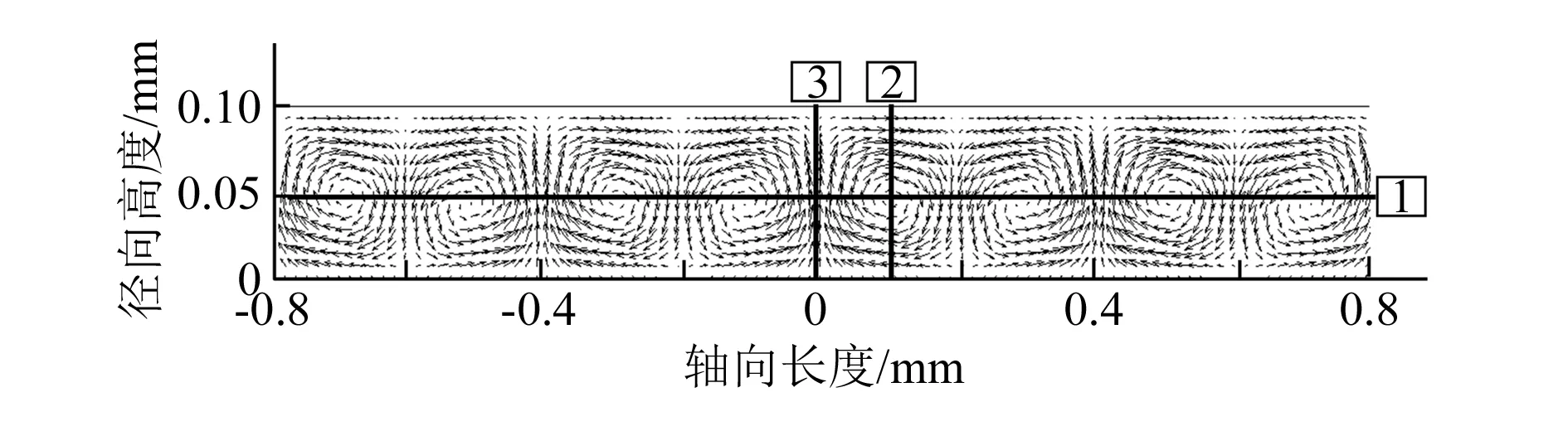
式中：λ=6.9×10-8，为空气平均分子自由程；l为特征尺度(这里认为是间隙高度)。本文中0.01

在数值计算时考虑采用Maxwell滑移速度边界条件，Maxwell一阶滑移速度公式如下[19]：

(13)

式中：uslip为滑移速度；ufluid为流体速度；uwall为壁面速度；σt为气体与壁面相互作用的动量协调系数；u为流向速度。式(13)中考虑了曲率和旋转运动对滑移行为的影响，因此引入切向速度梯度作为修正。

将数值计算得出的轴向周期性间隙流场在周向上的压力分布结果与文献[11]中的结果进行比较。文献[11]中使用(P-P0)R1δ2/(μv0)来表征压力的大小，其中P为绝对压力，P0为大气压力，v0为圆柱间隙内壁面速度，使用的修正雷诺数为0.8，设置偏心率为0.75。将间隙比分别为0.010和0.008的压力分布结果与文献中结果进行对比，可知两者的分布趋势和数值均具有较高的一致性，仅在最大无量纲压力附近存在较大计算误差且误差值小于10%，如图4所示。

图4 计算结果与文献结果对比

2 结果分析

在不同偏心率、转速和间隙比等工况条件下，对动压轴承微间隙内流动特性进行系统研究，从而更进一步了解微间隙内的流动机理。

2.1 微间隙内压力分布

随着微间隙的偏心率、间隙比和转速等几何尺度及工况的改变，间隙内压力会发生相应变化。图5呈现了圆柱微间隙剪切流动中间隙比为0.01、内壁面转速为60 000 r/min、对应雷诺数约为430时，偏心率为0.3～0.9的微间隙压力周向分布。图中横坐标为周向角θ，纵轴(P-P0)/P0表示无量纲压力[8]。由于动压效应的影响，最大无量纲压力值出现在最小间隙高度之前，此处称为高压区；而最小无量纲压力值出现在最小间隙高度之后，此处称为低压区，在最小间隙高度位置，压力梯度达到最大。随着偏心率的增加，高压区压力升高，低压区压力下降，最大无量纲压力值从0.024上升到0.157，最小无量纲压力值从-0.021下降到-0.110。

图5 周向压力分布随偏心率的变化规律

同时，在偏心率ε大于0.6的高偏心率状态下，无量纲压力极值随偏心率的增加速率加快。无量纲压力极值点的周向角位置随偏心率的增加发生明显移动，随着偏心率的增加，无量纲最大压力点沿旋转方向朝最小间隙高度处移动，最小压力点逆旋转方向朝最小间隙高度处移动，如图6所示。

图6 压力极值位置随偏心率的变化规律

间隙比为0.005～0.020时，无量纲压力周向分布如图7所示，此时偏心率为0.6，内壁面转速为60 000 r/min。随着间隙比的减小，高压区压力升高，低压区压力下降，最大无量纲压力值从0.014上升至0.244，最小无量纲压力值从-0.016降至约-0.170，且当间隙比小于0.010时，随间隙比减小压力极值上升速率增加。图8描述了不同间隙比下最大和最小压力极值点在周向上的位置变化。随着间隙比的升高，最大和最小压力点均沿逆旋转方向移动。

图7 周向压力分布随间隙比的变化规律

图8 压力极值位置随间隙的变化规律

在内壁面转速从5 000 r/min增加至150 000 r/min时，周向的无量纲压力分布如图9所示，此时偏心率为0.6、间隙比为0.010。此时随着转速的增加，动压效应增强，高压区压力升高，低压区压力下降，最大无量纲压力值从0.005上升至0.169，最小无量纲压力值从-0.004下降到-0.138。如图10所示，随着转速的增加，最大压力极值点变化平稳，而最小压力极值点则沿旋转方向朝最大间隙高度处缓慢移动，说明转速对压力极值点的位置影响有限。

图9 周向压力分布随转速的变化规律

图10 压力极值位置随转速的变化规律

2.2 微间隙内速度分布

由于微间隙内流体的黏性作用，使得流体速度呈现典型的剪切流动规律，同时受间隙尺寸、偏心率等因素的影响，间隙内不同区域的速度梯度会产生不同变化，图11呈现了轴向截面上速度分布规律。内侧壁面为旋转壁面，由于剪切力的作用，使得靠近壁面的速度最高，速度沿径向由内壁向外壁逐步降低。达到一定转速后，靠近外壁面一侧会出现与转速相反的流动，说明间隙内出现回流，回流的形成是楔形通道和压力梯度共同作用的结果，流动分离发生在收缩通道内，分离后的流体逆向流动，跨过最大间隙高度后在扩张通道内与主流重新附着。

图11 间隙内速度分布矢量图

图12呈现的是偏心率为0.6时，不同周向角θ处切向速度沿间隙高度(径向)分布情况，其中横轴表示无量纲间隙高度[15]，0和1分别表示内外壁面位置；纵轴表示无量纲切向速度v/v0，其中v为流体切向速度，v0为内壁面旋转速度。切向速度梯度大小在不同周向角位置存在差异，随着周向角的增大，靠近内壁面切向速度梯度由大变小，且周向角θ在0～0.5π内时切向速度在间隙高度0.6～1.0之间小于0，说明此范围内有回流存在。

图12 不同周向角处的切向速度分布

图13和图14分别表示间隙比为0.010、转速为35 000 r/min时，最大间隙与最小间隙高度处切向速度分布随偏心率的变化规律。在最大间隙高度处，速度变化率由内壁到外壁逐渐降低，而随着偏心率增大，速度梯度增大。当偏心率高于0.3时，靠外壁侧的切向速度小于0，这是由于间隙内产生回流，伴随着偏心率的升高回流现象会愈发明显。与最大间隙高度处相比，在最小间隙高度处，压力梯度明显更高，使得此处流场的速度更大，因此速度梯度呈现相反的分布。当偏心率增大时，最小间隙高度处的速度梯度略微减小。产生该现象原因是偏心率增大导致压力梯度增大，流体除受到剪切力外还受到压力驱动作用，因此此处的流动是剪切流与压力流共同叠加形成的，而流体受到的压力驱动弥补了由于偏心率的变化造成的压力梯度的不同，因此在最小间隙高度处，速度梯度较为接近。

图13 不同偏心率时最大间隙高度处切向速度分布

图14 不同偏心率时最小间隙高度处切向速度分布

较高偏心率引起间隙内出现回流，回流出现在大间隙一侧，在收缩通道内发生了流动分离，并在扩张通道重新附着。不同偏心率下的流动分离点和再附着点的周向角度发生变化，如图15所示。由于偏心率的升高，间隙通道的收缩和扩张更为剧烈，同时引起更大的逆压梯度，因此分离点和再附着点均向最小间隙高度位置移动，且回流区域的周向角跨度区域增大，如图16所示，当偏心率升高至0.8时，回流区周向角度跨度占比达到0.73。

图15 分离点和再附着点的周向角变化规律

图16 回流区周向占比

图17和18分别呈现了壁面转速为60 000 r/min、偏心率为0.6时，不同间隙比下最大和最小间隙高度处无量纲切向速度分布规律。由于压力场的作用，最小间隙高度处速度大于最大间隙高度处。但在不同间隙比下的切向速度变化趋势基本吻合，说明此时速度分布主要受压力变化的影响，而间隙比变化对速度分布影响较小。在不同间隙比下，间隙内均有回流的产生，说明间隙比不是回流产生的主要原因。

图17 不同间隙比时最大间隙高度处切向速度分布

图18 不同间隙比时最小间隙高度处切向速度分布

不同转速下的无量纲切向速度沿径向分布规律如图19和图20所示，此时偏心率为0.6、间隙比为0.010。同样由于压力场的作用，最小间隙高度处速度大于最大间隙高度处。在最大间隙高度位置，速度变化率由内壁向外壁逐渐减小；在最小间隙高度位置，速度变化率则相反。不同转速下切向速度分布几乎重合，且最大间隙高度处均有回流产生。综上说明，偏心率的增加使得楔形尺寸的变化和间隙内压力梯度是影响切向速度分布主要因素，同时回流的出现主要与偏心率有关。

图19 不同转速时最大间隙高度处切向速度分布

图20 不同转速时最小间隙高度处切向速度分布

对于偏心下的泰勒-库特流动，当转速达到临界值时，间隙内部分区域会出现泰勒涡流。本文获得了径向切面上速度矢量图，径向切面又称子午面。图21显示了间隙比为0.02、偏心率为0.6时，周向角θ=π位置处泰勒涡随转速升高的演变过程。当转速为34 000 r/min时泰勒数约为4 800，间隙内泰勒涡初步产生，当转速为35 000 r/min、对应泰勒数约为5 086时，间隙内泰勒涡之间大小形貌相等，且呈现两两对称周期性变化，每个涡流结构独立且流动相对封闭，此时涡流称为层流泰勒涡；当转速升至36 000 r/min、对应泰勒数为5 381时，涡流不再独立和封闭，涡流之间开始出现流动传递，速度矢量场为波浪形；当转速达到37 000 r/min、对应泰勒数为5 685时，速度矢量场表现出明显波浪形，并呈周期性变化，此时涡流已发展为波状泰勒涡；当转速达到50 000 r/min、对应泰勒数为10 381时，涡流结构被破坏，轴向周期性已不存在，但仍在部分区域存在涡流，此时涡流已发展成湍流泰勒涡。

图21 不同转速时间隙内速度矢量分布图

泰勒涡的出现会使间隙内的速度分布产生相应的变化，本文分别提取周向角θ=0.5π处子午面中轴线与径向线上数据，此时流场间隙比为0.02、偏心率为0.6、转速为35 000 r/min，如图22所示，其中横轴表示轴向方位，纵轴表示从内壁到外壁的径向高度，横线1为子午面中轴线，径线2和3分别位于涡心和两涡交界处，此转速下微间隙内刚好处于层流泰勒涡状态。

图22 轴线与径线位置示意图

其中轴向速度沿中轴线1呈波状分布，如图23所示，速度范围为-0.15 ～0.15 m/s。在泰勒涡心处轴向速度处于峰值，相邻的两涡速度相反，在涡的交界处轴向速度为0。径向速度沿中轴线1同样呈波状分布，速度范围为-0.25 ～0.40 m/s，在涡心处径向速度约为0，在两涡交界处径向速度达到峰值。由于剪切力的存在，切向速度值远高于径向和轴向速度，但泰勒涡的出现使得切向速度同样呈波状分布，切向速度峰值和谷值均位于两涡的交界处。

图23 子午面中轴线处速度分布图

图24和25呈现了在径线2和径线3上速度的分布。径线2上轴向速度呈近似正弦分布，并沿涡心对称，且方向相反，而经过涡心时径向速度为0。径线3上轴向速度约为0，径向速度呈现先增大后减小的趋势。由于剪切力的作用，径线2与3上的切向速度仍然遵循剪切流动下的速度分布，而泰勒涡的出现，使两处的速度梯度不再相同。

图24 径向和轴向速度分布图

图25 切向速度分布图

3 结束语

本文对旋转圆柱微间隙剪切流动特性进行了数值研究，分析对比在不同偏心率、间隙比和转速等条件下，微间隙内压力和速度分布的变化规律。结果表明，随偏心率或转速的增加、间隙比的减小，无量纲压力值的绝对值上升。在偏心率大于0.6、间隙比小于0.01时，压力极值变化速率加快，同时压力极值点随着偏心率的增加均向最小间隙高度处移动。回流的出现主要受到偏心率的影响，偏心率高于0.3时间隙内出现流动分离形成回流，当偏心率增加至0.8时，回流区周向角占比达到0.73。同时本文也获得了偏心下微间隙泰勒-库特流动规律，并验证了随着转速的增加，流动从层流泰勒涡至湍流泰勒涡的发展变化，以及泰勒涡的出现使得间隙内的速度呈现波状分布。