试谈“猜想”在初中数学教学中的作用

威信县第一中学 陈 洁

有一部分教师、家长和学生认为数学中的“猜想”是不动脑筋的乱猜、瞎想，总是觉得“猜”就是懒惰的表现，会误入歧途，不能在数学教学中大肆宣扬.我认为这是一种偏见，是对“猜想”的完全否定.“猜想”就是在已有数学知识和教学事实的基础上对未知量及其规律作出的似真判断.合乎情理的“猜想”往往蕴含着创造性思维活动，它有时可以发现真理，有时也可以发现解题的有效途径.纵观数学发展史，“猜想”有着极为重要的作用，如哥德巴赫猜想、黎曼猜想……在漫长的历史进程中，有些“猜想”可能被否决了，但随之而来的，可能是更多奇妙的发现.

在数学学科中，许多性质定理和判定定理可以说是通过“猜想”得以实现的.在证明一个数学定理之前，我们总是要先猜测这个定理的内容及其证明思路，甚至是一次又一次的不断尝试.在几次示范课中，我鼓励学生大胆“猜想”，通过“猜想”四个环节（实验→“猜想”的产生→“猜想”的验证→正确结论）的层层递进，激发学生的求知欲，教学效果较好，连学困生也能激起学习数学的兴趣.

一、典型案例分析和启示

案例1：垂径定理

在讲授“垂径定理”时，如果教师直接写出这一定理来加以论证，学生会感到太突然.教师不妨先让学生来“猜想”它的内容.

教师让学生课前准备一张圆形纸片，在上面任画一条弦AB，过圆心O作直径CD使CD⊥AB，垂足为E，这样就构建了“垂直于弦的直径”，如图1.接着，教师请学生把这个圆形纸片沿直径CD对折，让他们仔细观察分析，并提问：“同学们发现了什么？”学生甲回答：“弦AB被直径CD分成的两部分重合了.”学生乙回答：“弧AC和弧BC、弧AD和弧BD分别重合.”然后，教师引导学生产生“猜想”：垂直于弦的直径平分弦，并且平分弦所对的弧.接着，教师又问：“这一‘猜想’对吗？”然后引导学生对“猜想”进行验证.

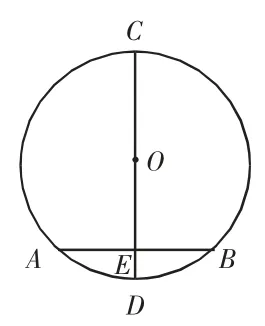
图1

这样一节课上下来，教师和学生都觉得非常轻松.学生在“猜想”的过程中，既动手又动脑，积极性较高，教学效果较好.

案例2：三角形内角和定理

“三角形内角和定理”这节课也可以用到“猜想”.学生在小学时就了解了“三角形内角和等于180°”的知识.在初中数学教学中，教师可以大胆地开展一些实验，让学生在实验中获得感性认识，去观察、分析、概括出产生的“猜想”，然后再加以验证.

教师让学生做一个三角形纸片，把它的三个角用不同方式拼在一起（如图2甲、乙），让学生观察三个角拼在一起好像构成一个平角.由此“猜想”：三角形三个内角之和等于180°.教师再提出疑问:“三角形内角和为什么是180°？”问题的提出激发了学生的求知欲。在拼图的过程中，学生通过观察不难发现原因，找到证明的途径.

图2

由此可见，实验不仅产生“猜想”，又为“猜想”的验证提供了很大的帮助.实践证明在数学教学中大胆“猜想”，有助于激发学生学习数学的兴趣和求知的欲望，从而增强他们学好数学的信心.

案例3：矩形的判定定理

在教学矩形的判定定理“对角线相等的平行四边形是矩形”时，教师可引导学生通过“矩形的对角线相等”这一性质进行“猜想”：对角线相等的四边形是矩形.讨论时，一位同学认为这个命题是对的，并且画出图形给大家看（如图3）.另一名同学说：“不行，我画出的图形不一样（如图4）.图4是等腰梯形，它的两条对角线也相等，但不是矩形.”通过讨论学生最后得出“对角线相等的四边形是矩形”的结论不成立。教师又引导学生“猜想”：“如果我们把四边形改成平行四边形呢？”学生讨论了一下找不出反例。接着，教师引导学生来证明这个“猜想”。

图3

图4

通过验证，教师和学生辨别出两个命题的真假，虽然“对角线相等的四边形是矩形”这一“猜想”被否决了，但是它可以让学生更牢固地掌握矩形的判定方法——“对角线相等的平行四边形是矩形”.

二、“猜想”在数学教学中有不可忽视的作用

1.“猜想”有助于调动学生学习数学的主动性和积极性.通过做实验产生的“猜想”，是有根由的，不是无缘无故的“瞎猜”.在做实验的过程中绝大多数学生都主动参与了活动，促进了独立思考、合作交流、反思质疑的良好学习习惯的形成.

2.“猜想”有助于帮助学生寻求解题的有效途径，有助于提高学生学习数学的兴趣，激发他们的求知欲.很多学生认为数学太难了，枯燥无味.“猜想”可以让他们在“玩”中“学”，在“学”中“玩”，积极参与学习活动，让他们感受到学习数学的乐趣，从而激发学习数学的兴趣.通过“猜想”的四个环节的层层递进，教师不仅让学生寻找到解题的有效途径，还激发了他们的求知欲望.

3.“猜想”有一个主要的环节，那就是验证.验证时，学生需要去分析问题、解决问题，亲自验证“猜想”的正确与否.这就让学生有了成功的体验，他们会觉得自己还“行”，从而增强了他们学习数学的信心.

4.“猜想”有助于学生辨析知识，提高他们的识别能力，增强在学习和生活中的判断能力.在案例3中，虽然有的“猜想”被否决了，但是学生“牢固”地掌握了矩形的判定方法，从另一个角度帮助他们识别对错，从而提高了他们的识别能力，让他们体验成功与失败，分享发现和成果.

5.“猜想”不但有助于提高学生的逻辑思维能力和空间想象能力，还有助于培养学生的创新意识和创造能力.