基于机器学习的区域救护车需求量预测模型的比较

刘 佳， 江慧琳， 王 静， 伍卓文， 李双明， 曾 睿， 罗一洲， 黄海铨， 茅海峰， 程 琦，伍宝玲， 陈晓辉

院前急救是急诊医疗服务的第一道防线。当前公共卫生医疗服务面临着人口老龄化、各种急危重症发病率的逐年增长以及各种突发自然灾害、事故灾害、公共卫生事件频发的情况，导致院前急救服务需求不断增加[1]。在救护车服务需求增加和卫生资源有限的背景下，及时预测救护车需求有助于战略性规划配置卫生服务资源以满足群众的需求，还可作为管理居民救护车需求溢出的预警。在临床领域中已有许多研究成功地运用不同的统计方法预测特定的疾病事件或疾病总例数等[2-4]，主要是运用机器学习和传统统计方法进行预测，大部分研究结果都展示出机器学习的预测效能要优于传统统计方法[5-6]。

有许多研究表明，天气因素对院前急救需求量有影响，比如温度[7-8]和PM2.5[9]，因此研究所用数据有时间、天气两类数据，时间数据是时间段数据，适合用于时间序列算法模型，所以考虑使用比较成熟稳定且使用频率较多的长短期记忆网络(long short-term memory， LSTM)，同时选用研究频率同样较多的极限梯度提升(eXtreme gradient boosting， XGBoost)分析数据进行对比，并进行预测模型性能评价，为救护车需求预测预警提供参考。

1 资料与方法

1.1研究设计和地点

本研究是一项回顾性研究，数据来源是2009～2018年某大学附属医院出车急救任务的120呼叫数据，呼叫数据均从广州市急救医疗指挥中心信息系统获取。本院位于广州市老城区之一海珠区，该区的常住人口106.73万人，60岁以上人口27.48万人。

本研究根据2009～2018年急救出车数据和天气数据数据集使用XGBoost和LSTM对每日救护车需求进行预测，并进行预测模型性能评价。

1.2数据类型

出车数据：从广州市急救医疗指挥中心院前急救调度系统收集到变量有六辖区每日院前急救呼叫量；气温数据：从国家气象局收集到变量有日最低温度(℃)、日最高温度(℃)、日平均温度(℃)、日平均湿度(%)、日平均风速(m/s)、日平均气压(hpa)、日平均能见度(km)、日总降水量(mm)、日平均总云量(%)。

纳入预测模型的自变量包含四个维度，分别是时间序列数据(星期、休息日)、天气维度(每日最低温度(℃)、日最高温度(℃)、日平均温度(℃)、日平均湿度(%)、日平均风速(m/s)、日平均气压(hpa)、日平均能见度(km)、日总降水量(mm)、日平均总云量(%)、救护车需求量滞后项(当前时间段的前一个时间段的需求量、当前时间段的前第二个时间段的需求量)、救护车需求变化量(前两个时间段救护车呼叫量做差值)。因变量是广州市六辖区每日院前急救需求量。将连续2天及以上没有救护车呼叫的数据作为缺失数据,做缺失处理。

1.3研究方法 纳入训练和测试的数据包括时间特征、天气特征和救护车需求量滞后特征。在XGBoost中，时间分解为月、日2个独立的变量，代表其时间背后的节假日、气候等其他因素。在LSTM中，把每日的出车数据与天气数据按照日期合并，将合并后的数据经过数据预处理操作后，搭建LSTM模型训练数据并预测救护车需求量结果。

1.4数据预处理

1.4.1 归一化处理 将救护车呼叫数据和天气数据按时间先后顺序排列，将呼叫量数据，进行归一化处理，即呼叫量数据统一转化为0～1之间的数。将数据进行归一化处理是模型预测过程中的基础，目的是让不同特征在数值上有一定比较性，便于比较不同特征[10]。数据归一化处理可以加快运算速度并防止迭代运算时的可能溢出，也可在一定程度上提升模型的精度。数据归一化公式：

1.4.2 滞后变量 考虑到疾病发生具有窗口期，因而救护车需求会随天气的变化有滞后效应，而院前急救需求量的数据是与时间序列相关的，所以有可能上一个时间段或更之前的时间段会影响到该时间段，因此考虑生成滞后项，让模型学习其中的规律，生成滞后项的步骤和计算方法如下。

(1)对数据按时间序列先后进行排序。

(2)生成2个滞后项(回溯2个时间段的需求量)，①一阶滞后项：当前时间段的前一个时间段的需求量；②二阶滞后项：当前时间段的前第二个时间段的需求量。

(3)生成1个需求量变化量 二阶滞后差分：一阶滞后项与二阶滞后项做差值。

本研究所有数据均使用Python3.6.7进行分析。

1.5模型选择 将可用数据的前70%数据作为训练集，后30%数据作为验证集，训练集通过使用训练机制训练模型。考虑到时间数据对救护车需求的影响较大，同时需要加入天气数据，因此选择使用时间系列模型和回归模型。

1.5.1 XGBoost XGBoost是一种集成决策树算法，可以将所有数据和特征纳入模型且保留记忆，即对大数据的处理能力强且能够储存重要的历史事件并加以标记。本研究中XGBoost模型做了如下几个优化：①XGBoost模型对损失函数同时使用了一阶导数和二阶导数，对损失函数进行二阶泰勒公式展开。②XGBoost模型不仅支持以CART决策树为基础的分类器，还支持线性分类器。③采用了列抽样(column subsampling)的方式。④XGBoost模型在特征层面上使用了并行运行操作。⑤XGBoost模型对目标函数添加了正则项。

1.5.2 LSTM LSTM是一种特殊的循环神经网络(RNN)算法，通常有3个阶段：忘记阶段、选择记忆阶段、输出阶段[11]。本研究中LSTM采用交叉熵作为损失函数，在反向传播中为降低损失，会不断地用学习数据进行迭代更新每个门以及计算步骤的权重系数W、U、b，从而引起每个细胞的细胞状态值进行更新变化。在反向传播的机制下，依然采用类似神经网络的梯度下降法来更新各个参数的权重系数。

1.6模型评价指标

利用测试集数据进行模型的性能评价，实际上是对模型预测需求量的准确性评价，模型性能通过平均绝对误差(mean absolute error, MAE)和平均绝对百分比误差(mean absolute percentage error, MAPE)指标评价。

MAE计算公式：

MAPE计算公式：

当MAPE<10%时，预测具有较高准确度；当MAPE 10%～20%时，预测具有良好的准确度；当MAPE 20%～50%时，预测是合理的；当MAPE>50%时，预测是不准确的[12]。而MAE的值越小则说明预测越准确。

2 结果

2.1院前急救需求情况

2009～2018年10年救护车呼叫数据共有40 014条，平均每个月的救护车需求量在330次左右，日最高呼叫量为42次，日最低呼叫量为0次。10年1月到12月平均救护车需求量的总体趋势是递增的，见图1。

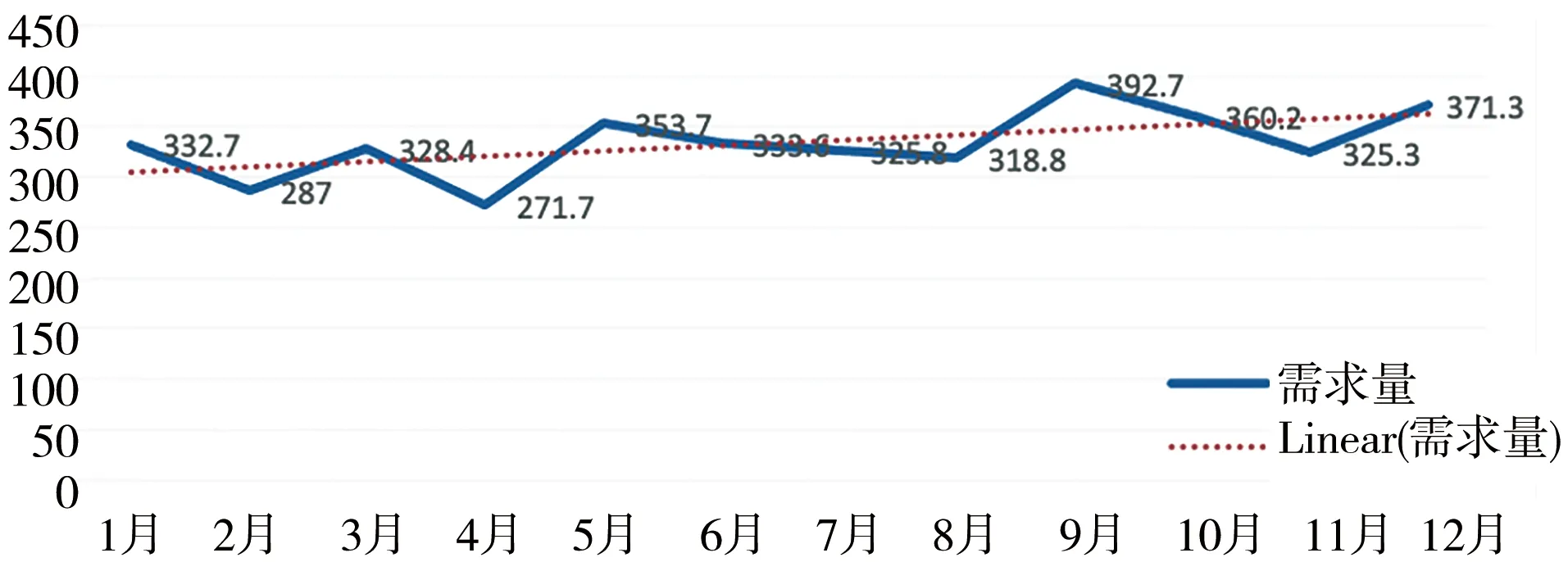
图1 广州市某大学附属医院每月平均救护车需求量

通过用移动平均法拟合曲线观察数据变化趋势，对比拟合正弦方法的红色曲线差异，拟合出的蓝线跟红线差距较大，没有明显的规律性，数据集并无季节性趋势。见图2。

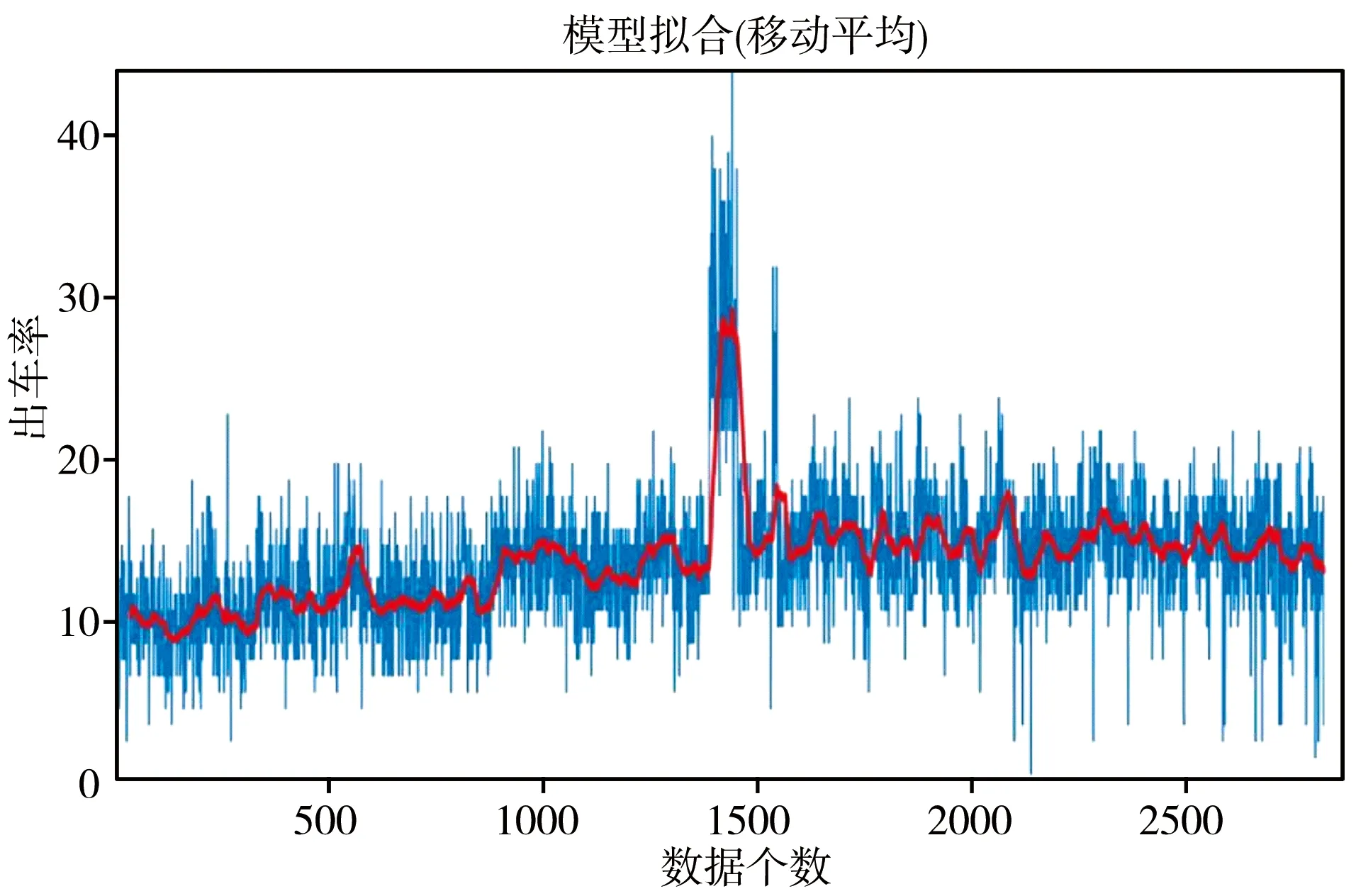
图2 广州市某大学附属医院救护车需求量曲线拟合季节模型

救护车呼叫时间段统计显示，救护车需求高峰期在早上8:00～11:00和晚上18:00～21:00，凌晨4：00～5：00的需求量最少。每小时平均救护车需求量分布见图3。

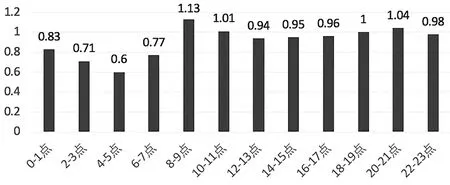
图3 广州市某大学附属医院每小时平均救护车需求量分布时间

2.2气候变化情况 气候数据共有3968条。广州市2009～2018年10年的日最低温度、日平均温度、日平均总云量和日平均湿度的总体变化趋势是一致的。日最低温度月均值是7月最高，1月最低；平均温度月均值是7月最高，1月最低；平均总云量月均值最高是4月，最低是10月；平均湿度月均值最高是6月，最低是12月。见图4。

图4 广州市2009～2018年天气特征每日变化图

2.3天气数据与救护车需求量的滞后关系

为了研究最高温度、最低温度和平均温度对每日救护车需求量的滞后影响，采用了阿尔蒙多项式方法，用最小二乘法做的格兰杰因果检验来检验模型优劣。具体公式如下：

yt=α+β0Xt+β1Xt-1+β2Xt-2+……+βkXt-k+μt

最高温度、最低温度和平均温度对每日救护车需求量的滞后分析都没有对出车有明显影响，见表1～6。

做y关于Z0、Z1、Z2的OLS回归，根据图1所示的输出结果，可计算出原分布滞后模型的参数估计值：α=14.3753，β0=0.05085，β1=0.009255。由R2=0.0052和可决系数R2=0.0042，可知最高温度对每日救护车出车数量并无显著影响，拟合优度较低，说明模型对样本的拟合效果不好。

表1 最高温度对每日救护车需求量的滞后分析

根据表2所示，当取滞后阶数为2期时，格兰杰因果关系检验既拒绝了x不是y的格兰杰原因的假设，也拒绝了y不是x的格兰杰因果关系检测结果。

表2 检验结果

做y关于Z0、Z1、Z2的OLS回归，根据图1所示的输出结果，由此可计算出原分布滞后模型的参数估计值：α=14.4718，β0=0.0863，β1=0.0036。由R2=0.0060和可决系数R2=0.0049，可知日平均温度对每日救护车出车数量并无显著影响，拟合优度较低，说明模型对样本的拟合效果不好。

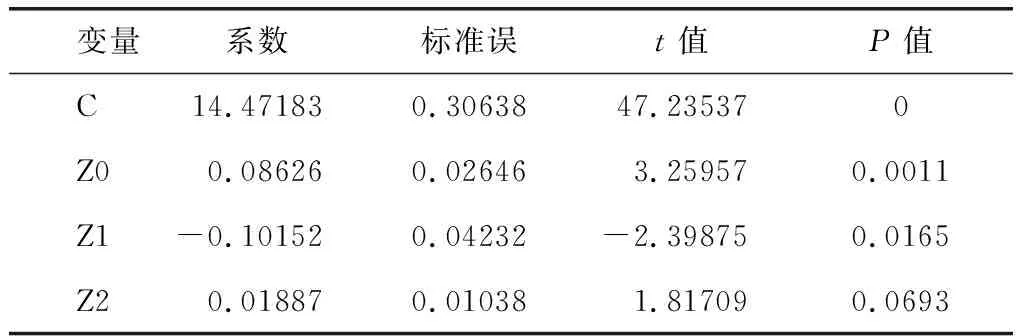
表3 日平均温度对每日救护车需求量的滞后分析

根据表4所示，当取滞后阶数为2期时，格兰杰因果关系检验既拒绝了x不是y的格兰杰原因的假设，也拒绝了y不是x的格兰杰因果关系检测结果。

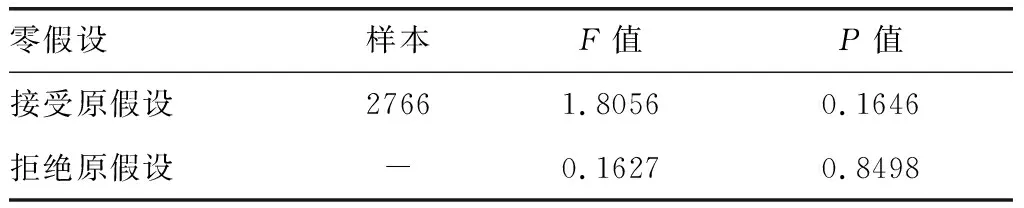
表4 检验结果

做y关于Z0、Z1、Z2的OLS的回归，根据图1所示的输出结果，由此可计算出原分布滞后模型的参数估计值：α=14.3794，β0=0.0664，β1=0.0052。由R2=0.0051和可决系数R2=0.0040，可知最低温度对每日救护车出车数量并无显著的影响，拟合优度较低，说明模型对样本的拟合效果不好。

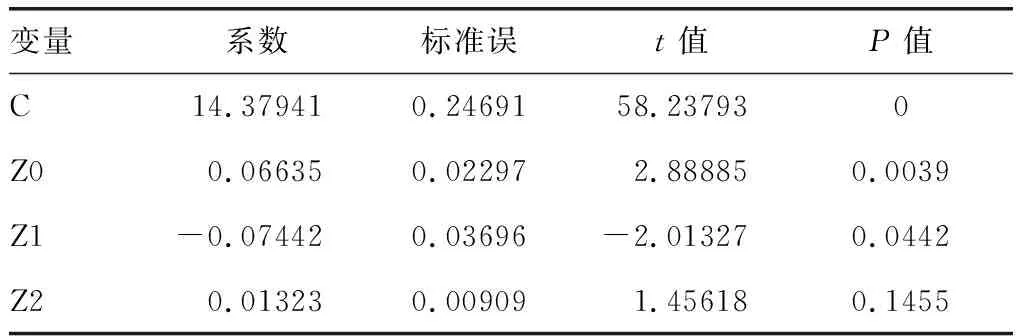
表5 最低温度对每日救护车需求量的滞后分析

表6 检验结果

2.4XGBoost和LSTM模型的预测结果 测试集中从XGBoost和LSTM模型的每日救护车需求量预测值和真实值对比见图5、6。从表7可得使用XGBoost模型预测每日救护车需求量的MAE值为2.692，MAPE值为24.29%；LSTM模型预测每日救护车需求量的MAE值为2.462，MAPE值为17.47%，因此LSTM预测每日救护车需求的准确性更高，且MAPE值<20%，说明LSTM模型预测具有良好的准确度。

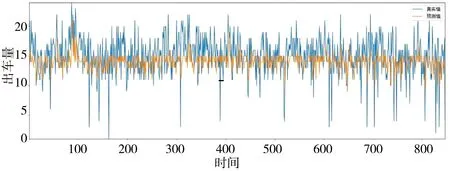
图5 极限梯度提升模型测试集中每日救护车预测值与真实值对比

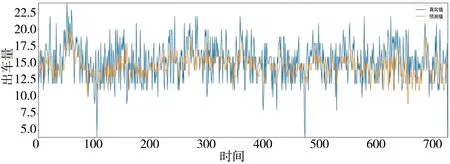
图6 长短期记忆网络模型测试集中每日救护车预测值与真实值对比

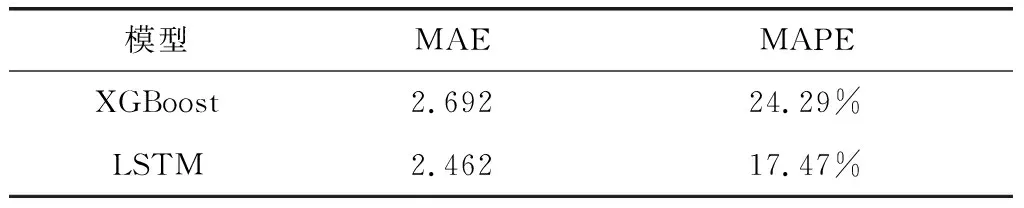
表7 XGBoost和LSTM每日救护车需求量预测性能比较

2.5院前急救需求量模型特征重要性分析 将天气和滞后项等影响救护车需求的特征通过XGBoost算法来计算特征重要性排序。特征重要性是一个缩放度量，其中日最低温度对救护车需求量影响最大，其余依次为日平均温度、出车量滞后项2天、出车量滞后项1天等，日总降水量对救护车需求量影响最小。见图7。

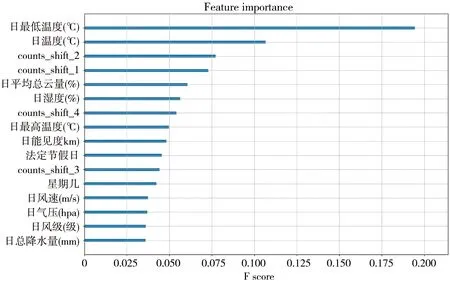
图7 极限梯度提升模型中特征重要性排序

3 讨论

本研究揭示了天气和日期与救护车需求的相关性，且日最高温度、日最低温度和日平均温度对救护车需求量无滞后影响，对模型的预测性能影响较大的前三个变量是日平均温度、出车量滞后项2天、出车量滞后项1天，提出了基于天气和日期特征的预测救护车需求模型，研究结果证明LSTM预测模型能较好预测区域救护车日均需求量。

国内外已有许多研究表明院前急救需求量的影响因素有天气因素、空气质量因素、社会经济因素等等，比如Miyatake等[13]选用各种气温参数，即气温平均值、最高气温平均值、最低气温平均值、最高气温值，并得出这些气温参数均与救护车的运输显著正相关。Sangkharat等[14]得出，救护车调度可以与极端温度相关，建议将气象因素纳入救护车预测模型。Chen等[15]选用O3、SO2、NO2、CO等污染物指标，结果显示，SO2和NO2、CO与哮喘急救车派遣呈正相关。对救护车需求量预测模型研究比较多的是时间序列模型，如Baker等[16]使用由Winters最初开发的指数平滑模型预测救护车需求。而最常用的模型为时间序列模型，Tandberg等[17]采用时间序列的方法(移动平均线、平滑移动平均线和自回归综合移动平均线)对连续两年救护车的每小时运行量、总运行时间、日期等数据构建预测模型，预测每小时救护车的运行量，结果显示，平滑移动平均线模型得出的预测是所纳入研究的模型中最准确的。还有研究使用多种预测模型进行对比，如Channouf等[18]通过消除趋势、季节性和特殊日子影响后获得的数据自回归模型和季节性ARIMA模型预测每日的救护车呼叫量，通过每小时呼叫量向量的多项式分布和将时间序列拟合到每小时级别的数据进行对比预测每小时救护车呼叫量，结果显示，每日呼叫量预测模型较好的是自回归模型，每小时呼叫量预测模型较好的是多项式分布模型。

本研究中使用的LSTM模型对某大学附属医院每日救护车需求量的预测价值优，因为LSTM为时间序列算法模型，相比于XGBoost对时间数据的学习效果更好，而XGBoost作为决策树模型更难学习到时间序列中的信息，因此LSTM模型更适合预测救护车需求量，且预测准确性也更高。准确性高的救护车需求量预测模型可以根据预测情况开通合理的调度席位数，避免出现急救电话呼叫拥挤、等候调度时间长等情况导致急救不及时，并可根据预测量提前制定应急方案，此外，还可以根据预测结果和院前急救资源分布的特征，合理配置院前急救资源，最小化临床风险。对急救网络医院来说可以根据预测情况在需求量高峰期安排充足的急救医护人员和急救药品等资源，保障患者及时获得院前急救服务。本研究也为日后救护车需求量预测的深入研究提供参考，后期研究可以进行特征工程或者增加多中心的研究样本量以进一步提高模型预测准确度。