知识传授与价值引导相结合的高校线性代数教学探究

张媛媛 张现强 毕晓芳 隋双侠

摘要：在高等院校，线性代数课程是重要的基础课程，教师在线性代数课堂教学过程中要将知识传授与价值引导结合起来，对学生进行价值观引导、思想品德教育及行为习惯的培养。文章结合作者所在学校以培养应用型人才为目标的办学定位，对在线性代数课程中开展课程思政教学的方式方法进行探索和阐述，并给出教学设计案例，展示教学过程，以实现知识传授与价值引导的双重目标。

关键词：课程思政；价值引导；线性代数；教学方法

中图分类号：G641；G642文献标志码：A文章编号：1008-3561（2022）29-0037-04

基金项目：本文系四川省民办教育协会2021年研究课题“课程思政背景下线性代数课程体系建设与实践”（MBXH21YB307）、西南财经大学天府学院“课程思政”示范课程建设项目（2021-130）的研究成果

2019年3月18日，习近平总书记在学校思想政治理论课教师座谈会上指出，“思政课是落實立德树人根本任务的关键课程”。2020年5月28日，《高等学校课程思政建设指导纲要》的印发，推动了高校各专业对课程思政教学探索和实施的进程。实现全员全程全方位育人，既要有惊涛拍岸的声势，也要有润物无声的效果，这是教育之道。教师在教学工作中要以知识为载体，强化知识传授中的价值育人功能。在高等院校，线性代数课程是重要的基础课程，修读学生都处于低年级，处于夯实知识基础的重要阶段，价值观形成的关键时期，所以教师在教学中要注意将价值引导与知识传授结合起来。文章结合作者所在学校以培养应用型人才为目标的办学定位，对在线性代数课程中开展课程思政教学的方式方法进行探索和阐述，并给出教学设计案例，以实现对学生价值观引导、思想品德教育及行为习惯的培养。

1.课程思政元素与教学管理结合

教师言传身教是教学的一部分。《世说新语·德行》记载：“谢公夫人教儿，问太傅：‘那得初不见君教儿？’答曰：‘我常自教儿。’”这说明了言传身教的重要性。教师积极的工作态度和良好的行为习惯，是学生最好的示范和榜样，所谓“身正为师”便是如此。教学管理要强调人性化管理，教师要以身作则。学生只有感觉到教师的“身正为师，德高为范”，才能给予教师更多尊重和信任。

2.课程思政元素与知识点结合

（1）在教学中融入马克思主义哲学思想。数学的魅力在于其深刻的“思想”。数学思想是数学的灵魂，是对数学事实与理论经过概括后产生的本质认识。所以，数学教学不应是讲授知识那么简单，而应把教学重点放在对数学思想和数学方法的引导上。只有以“思想引领”为主导，开展教学实践活动，才能更好更长远地影响学生。在遥远的古希腊时期，数学与哲学是当时文明与智慧的象征，二者之间是对立统一的关系。可以说，线性代数课程内容中便蕴含着丰富的哲学思想。因此在教学中，同一个知识点可以融入不同的课程思政元素，同一个课程思政元素也可以与不同的知识点相结合，如表1所示。教师可以通过设计教学案例，将马克思主义哲学思想等课程思政元素融入教学内容，帮助学生树立正确的世界观、人生观、价值观。

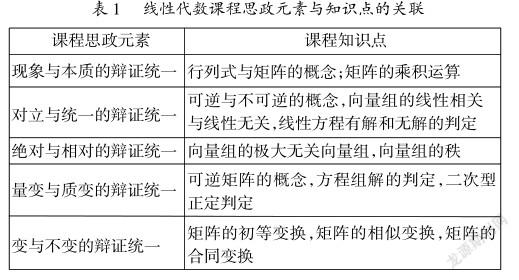
1）现象与本质的辩证统一。任何本质都需要现象来体现其特点和性质，数学就是由表及里探索其本质规律的学科。行列式与矩阵，外在相似，但行列式的本质是一个数值，而矩阵是一个数表。行向量和列向量作为特殊矩阵，在乘积运算中，行向量左乘列向量与行向量右乘列向量，前者结果是一个值，后者结果是一个方阵，其本质不同。学生只有透过表面现象认识到问题的本质，才能不混淆、不会产生错误认知，从而形成透过现象探索事物本质的思想。

2）对立与统一的辩证统一。矩阵可逆与不可逆的概念、向量组的线性相关与线性无关、线性方程组解的存在性判定、方阵对角化判定等内容，都蕴含着对立与统一的关系。教师借助这些内容可以教会学生运用对立与统一的关系，做到由此知彼。

3）绝对与相对的辩证统一。向量组的极大无关向量组和向量组的秩，通过对有限向量组进行初等行变换，得到的行最简形矩阵，来得到向量组的极大无关向量组，但极大无关向量组一般不唯一；由于向量组的秩始终不变，因此极大无关向量组包含的向量个数不会随着选取的极大无关组的改变而改变。这可以让学生懂得绝对与相对的辩证统一关系。

4）量变与质变的辩证统一。矩阵是否可逆，是通过其行列式的值是否为零来判定的。方程组是否有解，是通过比较方程组系数矩阵和增广矩阵的秩是否相等来判定的。二次型是否正定，是通过二次型矩阵的特征值来判定的。它们的共性都是通过“量”来确定“质”，这可以让学生学会运用量变与质变的辩证统一关系。

5）变与不变的辩证统一。矩阵进行初等变换，其秩不变；矩阵进行相似变换，其特征值不变；矩阵进行合同变换，正负惯性指数不变，体现了“形变质不变”的辩证思想。这可以让学生认识变与不变的辩证统一关系。

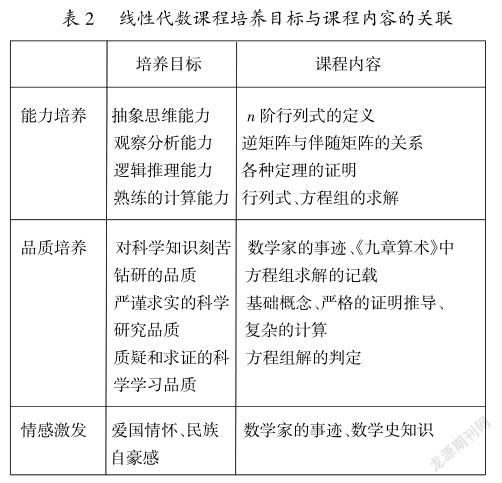
（2）在教学中培养学生优秀的品质和能力。线性代数课程培养目标与课程内容的关联，如表2所示。教师在教学中要结合课程内容对学生进行品质和能力的培养。

1）数学学科的一大特点就是对具体事物进行数学语言的抽象概括，这在线性代数课程中尤为突出。要以教学内容为载体，进行课程的合理设计，将能力培养目标融入教学过程。比如通过观察三阶行列式展开项的规律，概括推理出其展开形式，以培养学生抽象思维能力；通过对伴随矩阵的性质公式和逆矩阵定义式的比较及转换，得到逆矩阵与伴随矩阵的关系式，以培养学生观察分析能力和逻辑推理能力。本课程还涉及行列式计算等诸多计算，可以培养学生的计算能力。

2）教师在教学中要有意识地培养学生不怕困难、积极探索的品质。比如讲解线性方程组和矩阵的初等变换时，可以介绍我国著名的数学著作《九章算术》。该著作中的第八章采用分离系数法表示线性方程组，而这与现在的矩阵或向量组表示方程组一样。《九章算术》成书于公元1世纪左右，而在西方17世纪莱布尼兹才提出完整的线性方程的解法法则。向学生介绍我国的数学文化史，不仅能增强学生的民族自豪感及爱国情怀，而且有利于培养学生对科学知识刻苦钻研的精神品质。教师应要求学生注重细节，比如在矩阵的初等变换中，对每一个步骤都不能大意，在知识面前，要永远严谨、认真，养成严谨求实的科学研究品质。另外，在学习和科学研究中，质疑的精神是推动科学发展的动力。因此，教师要引导学生大胆质疑和猜想，用所学知识验证相关知识，培养学生良好的学习意识和学习习惯。

3）教师可以讲述我国数学家的故事，激发学生的家国意识和爱国情怀。在新中国成立初期，华罗庚拒绝了美国高薪待遇，克服重重困难踏上回国之路，并在归途中写下了《致中国全体留美学生的公开信》，呼吁“为了抉择真理，我们应当回去；为了国家民族，我们应当回去；为了为人民服务，我们也应当回去；就是为了个人出路，也应当早日回去，建立我们工作的基础，为我们伟大祖国的建设和发展而奋斗”，激励了一代又一代学子学成归来，报效祖国。华罗庚耗尽毕生智慧和精力，为中国数学事业发展做出了巨大贡献，被誉为“人民的数学家”。

3.课程思政元素与知识的应用和拓展结合

教师在教学中应带领学生积极探索“数学之用”，这也是很多学生所关注的问题。数学之用的体现涉及生活的方方面面，需要教师带领和引导学生去发现。当前，学生所认为的“有用”往往比较狭隘，他们更注重技术性的应用功能。这就需要教师引导学生思考和探索———知识在你还没看到“有用”的时候，是否就不值得学习了呢？对此，教师可以将课程知识与“数学之用”结合起来，引导学生思考。比如对于矩阵的奇异值分解，在自然语言处理中，最常见的文本按主题分类都是通过矩阵运算得以实现的，其实就是计算两个文本的相关程度。教师在课堂上可以借助网络资源，播放视频介绍关于文本分类的实质，带领学生探索更多的“数学之用”，让学生明白“有用之用”与“无用之用”之间的辩证统一关系。

课程思政教学不仅要充分挖掘课程中的思政元素，还要在课程设计环节以教学内容为载体，将课程思政元素合理、自然地融入，切忌生拉硬拽和强行说教。下面分享一些教学设计案例，如表3所示。

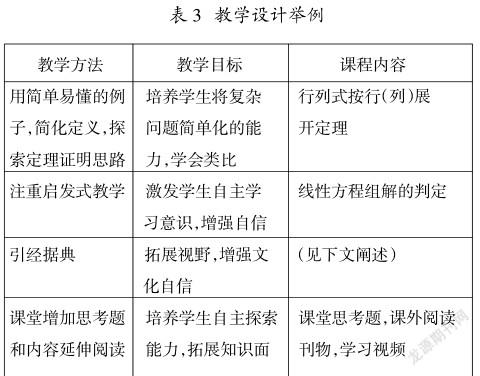
1.用简单易懂的例子，简化抽象的定义，帮助学生探索定理证明思路

学习余子式和代数余子式的定义，教师先给出概念：在n阶行列式中，把元素aij所在的第i行和第j列划去后，留下来的n-1阶行列式叫元素aij的余子式，记作Mij，把Aij=（-1）i+jMij称为元素的代数余子式。接着，教师用简单的例子，帮助学生快速理解定义，让学生在例子中注意到余子式和代数余子式的实质依然是行列式。同时，用简单的例子帮助学生理解定理和分析定理的证明。教师用例子简化抽象的定义，可以让学生轻松理解定理，学会从特殊到一般的解决问题的方法，用类比的思维方式学习新的知识。

2.注重启发式教学，激发学生自主学习意识

学习线性方程组解的判定内容时，教师先用例题引入。课堂上要留时间让学生练习，运用已学过的对增广矩阵进行初等行变换的方法求解，若变换得到的行阶梯型矩阵形如下：

学生则很容易发现，还原出来的方程组中出现了0=2的矛盾式，从而判断该方程组无解。这时，教师再引导学生观察系数矩阵和增广矩阵的秩的情况，总结对应方程组的解与矩阵秩的关系，接着展开讨论，得出方程组解的判定结论。在学生练习和讨论的过程中，教师要给予鼓励性评价，这样学生就会更有信心地进行自主学习，大胆推导，提高学习效率。

3.恰当引经据典，拓展视野，增强文化自信

在举例时，教师可以引用《论语》中的“知之者不如好之者，好之者不如樂之者”，让学生明白主观能动性的发挥对提高学习效率的重要性。还可以引用《荀子》中的“不闻不若闻之，闻之不若见之，见之不若知之，知之不若行之”，来强调动手练习的重要性，鼓励学生勤加练习，巩固知识，从而达到“温故而知新”的效果。

为掌握课程思政教学效果，课题组在学期末进行了问卷调查，调查内容包括是否体会到价值的引领作用、是否提高了学习意识和学习能力、是否增强了爱国意识和文化自信、是否提高了数学学习兴趣等。为保证数据的真实性，该调查采用实名制形式收集数据，共有100人参与问卷填写，收到有效问卷96份。

数据显示，大多数学生对线性代数课程思政教学比较接受和认可，期末考试成绩也在一定程度上反映了课程思政教学的良好效果。课题组根据学校开展课程思政特色示范课程工作的要求，进行了教学评价，详见表4。

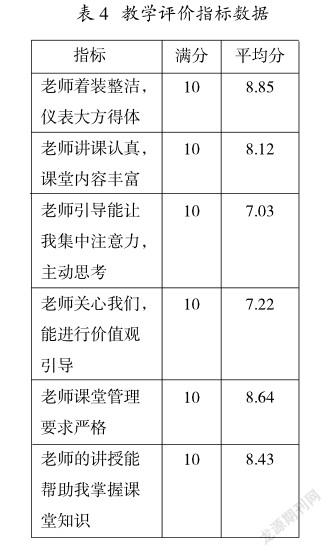
數据显示，思政课程内容起到了积极的作用，学生对其比较感兴趣。但同时，平均得分也反映出线性代数课程思政建设还需要进一步探索和积累经验。课程内容需要进一步挖掘思政元素，教学过程需要精心设计，要更自然地将知识和思政元素相结合。此外，教师在教学中发现，不少学生更关心期末考试成绩，对教师安排的课程思政教学活动不太感兴趣，对探索性学习重视不够。为此，教师在接下来的教学工作中要探究更加有效的教学方法，优化考核方式，调动学生主动探索的积极性，提高学生的学习意识和学习能力。

总之，以课程思政理念引领教学，能有效实现线性代数课程教书育人的目标。教师要全面融入课程思政元素，注重课程知识与思政元素的结合，在潜移默化中实现价值和思想的引领，提高学生学习的主动性，提升学生的学习能力，熏陶其品质，培养其良好的行为习惯。在今后的线性代数教学工作中，课程组教师成员间要相互学习，相互促进，共同探索知识传授与价值引导相结合的课程思政教学方法，完善教学资源，进一步提升课程思政教学效果。

参考文献：

[1]何薇，陈建龙.线性代数课程思政教学案例的设计与实践[J].大学数学，2021（05）.

[2]张景中.数学与哲学[M].大连：大连理工大学出版社，2008.

[3]陈航.数学课程思政的探索与实践[J].中国大学教学，2020（11）.

[4]张启明，徐承杰，汤琼，等.寓教于乐润物无声———例谈线性代数教学中课程思政的实施[J].数学学习与研究，2020（28）.

[5]吴军.数学之美[M].北京：人民邮电出版社，2014.

[6]吕宁.高校“思政课程”与“课程思政”协同育人的思路探索[J].大学教育，2018（01）.

Research on Linear Algebra Teaching in Colleges and Universities by Combining Knowledge Teaching with Value Guidance

Zhang Yuanyuan， Zhang Xianqiang， Bi Xiaofang， Sui Shuangxia

（Tianfu College of SWUFE， Sichuan Province， Mianyang 621000，China）

Abstract： In colleges and universities， linear algebra course is an important basic course. Teachers should combine knowledge teaching with value guidance in the process of linear algebra classroom teaching to guide students in values， ideological and moral education and behavior habits. Combining the school running orientation of the author’s school with the goal of cultivating application-oriented talents， this paper explores and expounds the ways and methods of carrying out curriculum ideological and political education in linear algebra courses， and gives teaching design cases to show the teaching process， so as to achieve the dual goals of knowledge teaching and value guidance.

Key words： curriculum ideologicalandpoliticaleducation； value guidance； linear algebra；teachingmethod