深度思考 揭示本质 提升能力
——2022年全国Ⅰ卷第21题的研究之旅
2022-10-17许家钊
许家钊
(苏州大学附属中学,江苏苏州,215000)
2022年高考已落下帷幕,对于全国Ⅰ卷,学生普遍感觉难度较大.笔者仔细研究了试题之后,发现数学试题紧扣高中数学的主干内容与重点知识,突出了对关键能力的考查,体现了立德树人根本任务.本文以第21题第1小题为例,通过一题五问,试图揭示解析几何中斜率之和与斜率之积的本质.
1 试题再现 感受高考
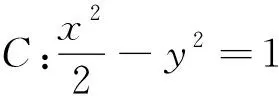
简要分析本题属于探索创新情景.考生感到困难,可能有三个原因:一是考试剩余时间不够导致心理慌张,二是本题设问较平时有所提前,三是模型不熟悉、算理不清楚、运算能力弱.本题实际上是解析几何中的常规问题——定值定点问题,只要两条直线AP,AQ的斜率之和为0,那么直线PQ的斜率就是定值,运算上体现了解析几何常规的“三步曲”——联立方程写韦达、题设条件代数化、韦达代入寻结果.
第一步 联立方程写韦达
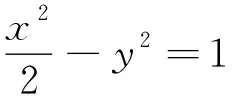

(1)
第二步 题设条件代数化

去分母整理得2kx1x2+(m+1-2k)(x1+x2)-4(m-1)=0,
(2)
第二步 韦达代入寻结果
将(1)式代入(2)式化简得2k2+km+k+m-1=0,
分解因式得(k+1)(2k-1+m)=0,
(3)
因为PQ不经过A点,故2k-1+m≠0,所以k=-1,即l的斜率为-1.
2 深度思考 揭示本质
探究1是因为特殊的A点才导致l的斜率是定值的吗?对于双曲线上任一定点A(x0,y0)呢?
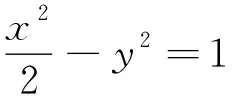

(4)
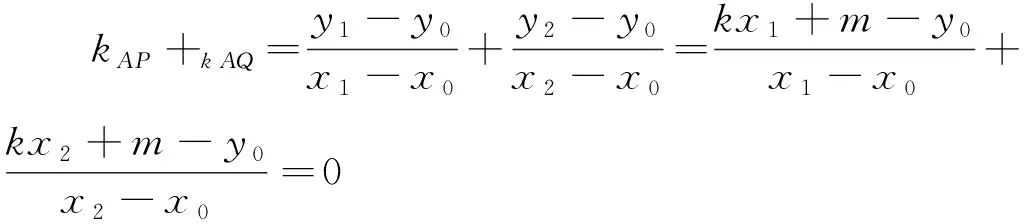
去分母整理得2kx1x2+(m+y0-kx0)(x1+x2)-2x0(m-y0)=0,
(5)
将(4)式代入(5)式化简得2kmy0+2k+a2k2x0y0+x0m-x0y0=0,整理得(2kmy0+x0m)+(2x0y0k2+2k-x0y0)=0
即m(2ky0+x0)+(2ky0+x0)(kx0-y0)=0,分解因式得(2ky0+x0)(m+kx0-y0)=0
(6)

反思将x0=2,y0=-1代入上述结果,得k=-1,与高考试题的答案一致.



(7)
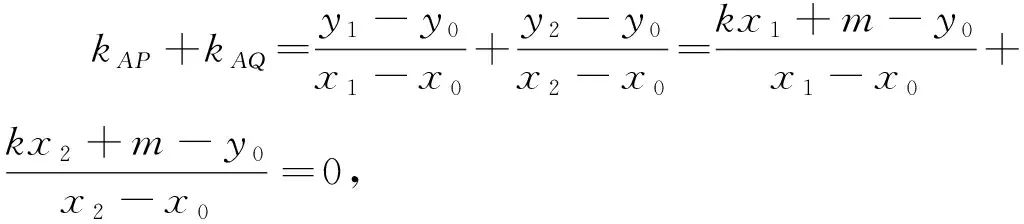
去分母整理得2kx1x2+(m+y0-kx0)(x1+x2)-2x0(m-y0)=0,
(8)
将(7)代入(8)化简得a2kmy0+a2b2k+a2k2x0y0+b2x0m-b2x0y0=0,
整理得(a2kmy0+b2x0m)+(a2x0y0k2+a2b2k-b2x0y0)=0,
即m(a2ky0+b2x0)+(a2ky0+b2x0)(kx0-y0)=0,
即(a2ky0+b2x0)(m+kx0-y0)=0,
(9)


方法优化对探究2中的坐标系进行平移,将坐标原点平移至A(x0,y0)处,

(10)
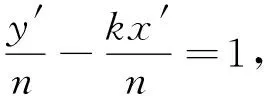
(11)
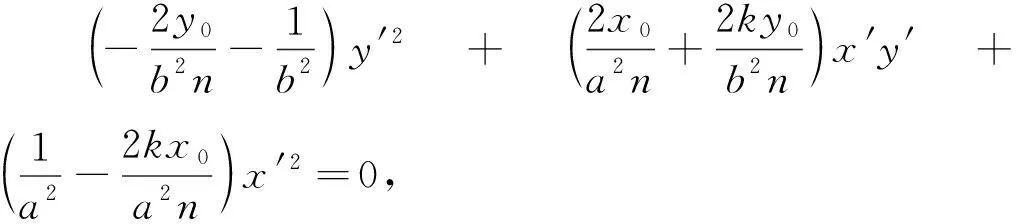


(12)
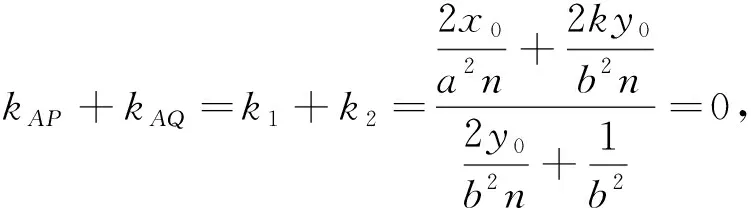
反思不妨将上述方法称为平移齐次化法,它的要点在于将坐标系原点平移至题中所给出的定点,写出对应的圆锥曲线方程和直线方程之后,进行齐次化联立,构造关于斜率k的方程,从而斜率之和及斜率之积便直接转化为两根之和与两根之积,避免了复杂的运算.

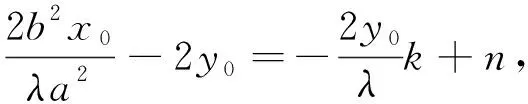
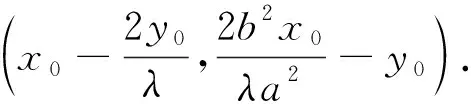
反思说明当斜率之和为非零常数时,PQ的斜率将不再是定值,而是恒过一定点.


(13)
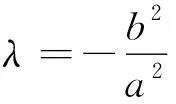


基于以上4个探究,我们得出如下定理:

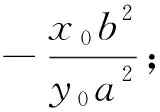
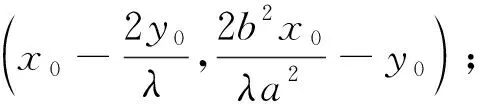
用同样的方法我们可以得到:


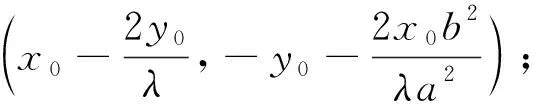
定理三对于有心二次曲线Ax2+By2=1(AB≠0)上一定点P及两动点A、B;
1) 若kPA+kPB=λ,
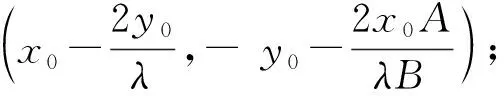
λ=0时,直线AB的方向向量为(y0B,x0A)
2) 若kPA·kPB=t,
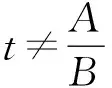
3 高考回看 温故知新


4 加强反思 提升能力
从近三年的高考数学来看,解析几何的解答题考查内容主要覆盖直线、椭圆、双曲线及抛物线,考查考生数学思维、数学应用、数学探索等,为进一步做好2023届高三数学解析几何一轮复习工作,笔者给出以下建议:
(1) 回归教材,注重基础,建构知识网络
对比发现,高考试题大都由课本习题改编而来,源于课本,而又高于课本.因此,高三数学一轮复习要回归课本,重视课本题目的外延与内涵,使学生了解知识的发生、发展和应用过程.
(2) 多角度思考,注重一题多解,优化方法
一方面,解析几何问题的本质是几何问题,利用题干图形的几何性质解答,往往能避开繁琐的代数运算,起到出奇制胜、事半功倍的效果.因此,在平时教学中,要训练考生准确作图和识图能力.
另一方面,代数法是解决解析几何问题的通性通法,解析几何试题一般入口较宽,很容易找到解决问题的思路,但是不同解法间运算量的差异很大.因此,在复习过程中,要多角度审视试题,注重不同方法的分析与比较,以便学生在今后的做题中迅速发现最优化的方法.
(3) 加大训练力度,着重培养学生逻辑推理和运算求解能力
根据高考评价体系的整体框架,高考数学学科提出了五大关键能力:逻辑思维、运算求解、空间想象、数学建模和创新能力.解析几何问题是中学数学的综合应用问题,对于逻辑思维能力和运算求解能力要求较高.好的思路是通过一定的推理、运算等数学语言表达出来的.
