一类二次规划问题的比例时滞神经网络的渐近稳定性

孙颖倩，周立群，王 宇，张诗茹，张渝佶

（天津师范大学数学科学学院，天津 300387）

二次规划问题是一类非线性规划问题，其在投资组合、决策规划和资源分配等方面具有广泛应用.由于非线性规划问题难以求得精确解，多数情况采用近似或局部最优解代替.文献[1]给出了一类利用神经网络求解线性规划问题的良好方案，但仅能保证局部最优解.为优化非线性规划问题的求解方案，文献[2]引入了时滞项，利用Lagrange函数构造时滞神经网络，解决了一类等式约束的二次规划问题，给出了解的存在性和系统渐近稳定性的判定准则.文献[3]在不涉及Lagrange乘子，不考虑原始对偶问题的情况下，利用投影的方法求解了一类有界约束的凸二次优化问题.文献[4-7]利用不同的时滞投影神经网络对二次规划问题进行求解，分别利用线性矩阵不等式、Lyapunov泛函和内积的性质研究了神经网络平衡点的稳定性.

比例时滞是一种无界时变时滞，其无界性给比例时滞系统的动力学研究带来许多困难.2011年，周立群将比例时滞引入到神经网络中，对比例时滞项的处理提出了一些较好的方法.目前，比例时滞神经网络动力学研究已经取得了一些进展.如，文献[8-9]分别利用特殊线性变换和Poincaré映射证明了比例时滞神经网络平衡点的存在性，利用M矩阵的性质和Lyapunov泛函研究了全局渐近稳定性和多项式稳定性.文献[10]利用同胚映射证明了多比例时滞神经网络平衡点的存在性，并利用时滞微分不等式给出全局指数稳定性的判定准则.文献[11]利用不动点定理的方法证明了比例时滞神经网络的周期解的存在性，通过构造时滞微分不等式得到了系统反周期解的指数稳定性的判定准则.文献[12]应用Lyapunov泛函的方法给出了具比例高阶广义细胞神经网络全局指数周期性的充分条件.文献[13-14]利用Lyapunov泛函和非线性矩阵不等式，讨论了比例时滞神经网络的指数同步性、多项式同步性和无源性.此外，文献[15]利用内积性质和Lyapunov泛函分析了一类具比例时滞细胞神经网络的散逸性.

本文在文献[6，15]的基础上，针对一类二次规划问题，利用Lagrange函数法和鞍点定理构建比例时滞投影神经网络，利用范数性质研究该网络的解的存在性，通过非线性变换和构造合适的Lyapunov泛函以及内积的性质探讨了比例时滞投影神经网络的全局渐近稳定性，并说明神经网络平衡点即为二次规划问题的最优解.最后通过数值算例及其仿真验证了所得准则的合理性和有效性.

1 预备知识和模型建立

记I∈Rn×n为单位矩阵.对任意矩阵X∈Rn×n，X＞0表示X为正定矩阵.C（[qt0，t0]，Rn）表示从[qt0，t0]到Rn的所有连续函数φ构成的集合.PΩ：Rn→Ω为一个投影算子，且对任意x〈·，·〉表示内积，〈y，y〉=‖y‖2，y∈Rn.‖·‖为欧几里得范数，对任意，其中λmax（ATA）为矩阵ATA的最大特征值.

考虑二次规划问题

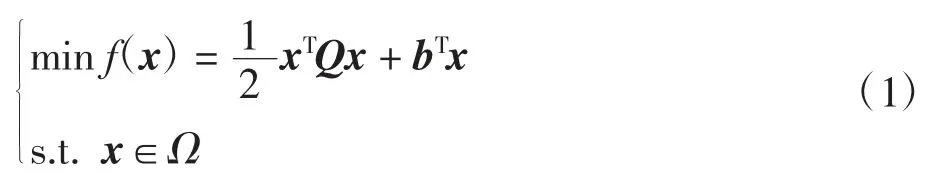
其中：x=（x1，x2，…，xn）T为决策变量，b∈Rn，Q为半正定矩阵，可行域Ω⊂Rn为一闭凸集.

针对问题（1）构造具比例时滞神经网络：

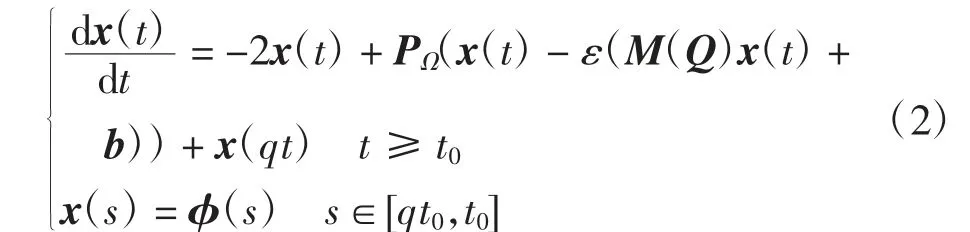
其中：x（t）=（x1（t），x2（t），…，xn（t））T为神经元在t时刻的状态变量为比例时滞因子，满足0＜q≤1，qt=t-（1-q）t，（1-q）t=τ（t）为时滞函数，当q≠1，t→+∞时，（1-q）t→+∞，即时滞函数为无界函数；x（s）=φ（s）为初值函数，t0≥1，φ（s）∈C（[qt0，t0]，Rn）.

定义1设称为Q的对称分支.若M（Q）为实对称正定矩阵，则称Q为亚对称正定矩阵；若M（Q）为半正定矩阵，则称Q为亚半正定矩阵.

定义2[16]称系统（2）的解x*是全局渐近稳定的，若x*是稳定的，且对任意初始函数ξ（t），有

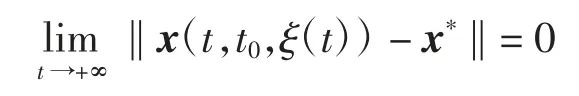
定义3对于二次规划问题

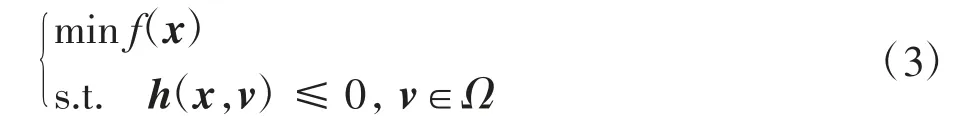
其中h（x，v）=x-v.问题（3）的Lagrange函数定义为

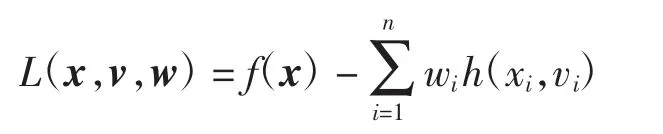
其中：v=（v1，v2，…，vn）T，w=（w1，w2，…，wn）T，wi＜0，i=1，2，…，n.满足

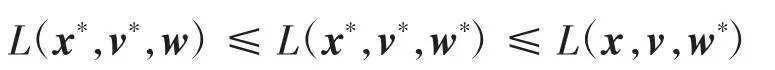
的（x*，v*，w*）称为L（x，v，w）的鞍点.

引理1[6]（投影定理）x*是变分不等式问题（xx*）TG（x*）≥0的解，当且仅当x*满足投影方程

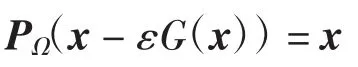
其中ε为任意正数.

引理2[17]令x（s）和u（t）为定义在[a，b]上的非负实值连续函数，u（t）≥0且在[a，b]上可积，若对任意t∈[a，b]，有成立，且g（t）是单调不减的函数，则有

引理3[18]设Ω⊂Rn为一闭凸集，投影算子PΩ有如下性质：

（1）对任意x、y∈Rn，有

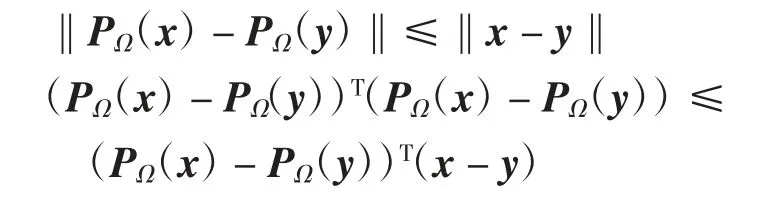
（2）对任意w∈Rn，r∈Ω，有

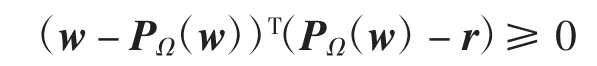
引理4[16]对任意φ（t）∈C（[qt0，t0]，Rn），系统（2）在[t0，T]上存在唯一的连续解x（t），满足初始条件x（t）=φ（t），t∈[qt0，t0]，且x（t）在[t0，T]上有界，从而系统（2）的解的存在区间可以延拓到[t0，+∞）.

引理5问题（3）的解x*=（x*1，x*2，…，x*n）T满足（x*，v*，w*）是L（x，v，w）=f（x）-wTh（x，v）的鞍点，其中v*=（v*1，v*2，…，v*n）T，当且仅当存在x*∈Ω（Ω⊂Rn为非空凸集），w*=（w*1，w*2，…，w*n）T，w*i≤0，满足如下条件：

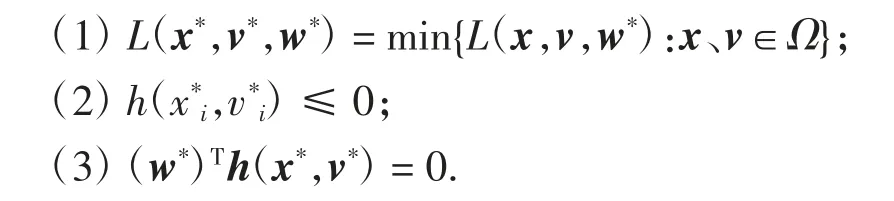
证明首先证明，若存在x*、v*和w*，使得（x*，v*，w*）满足引理5的条件（1）～（3），其中x*为问题（3）的解，则（x*，v*，w*）是L（x，v，w）的鞍点.

由条件（1）可得

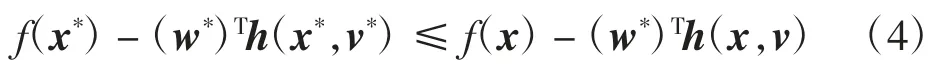
由条件（2）以及Lagrange乘子w≤0可得

将x*和v*代入L（x，v，w），由式（5）可得

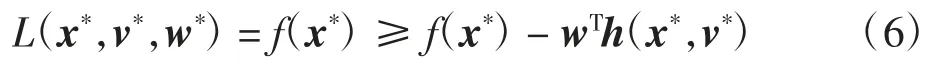
因此，由式（4）和式（6）可得

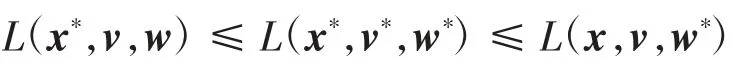
由定义3知，（x*，v*，w*）为L（x，v，w）的鞍点.

下面证明若（x*，v*，w*）为L（x，v，w）的鞍点，则x*为问题（3）的解.

设（x*，w*，v*）为L（x，v，w）的鞍点，则（x*，v*，w*）满足

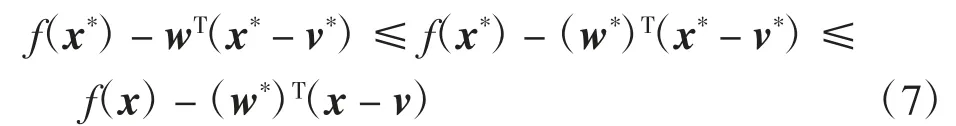
由式（7）的第1个不等式，对任意w∈Rn，有（w-w*）T·（x*-v*）≤0成立，所以x*=v*，x*∈Ω.由式（7）的第2个不等式得

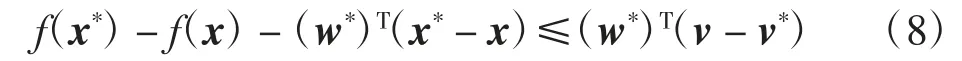
将x*=v*代入式（8），得

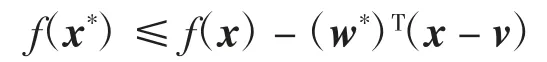
由w*i≤0，i=1，2，…，n，x-v≤0可得f（x*）＜f（x）.因此x*是问题（3）的解.引理证毕.

注1由上述证明可知，问题（3）的Lagrange函数的鞍点（x*，v*，w*）满足x*∈Ω，且f（x*）≤f（x），x∈Rn.因此x*也是问题（1）的解，求解问题（1）即求解问题（3）的Lagrange函数的鞍点.

下面证明问题（1）的解x*为系统（2）的平衡点.

由引理5的证明知，若（x*，v*，w*）为问题（3）的Lagrange函数L（x，v，w）的鞍点，由式（8）有

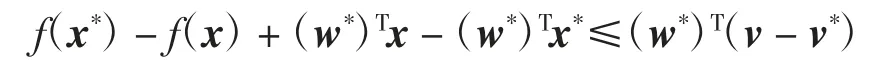
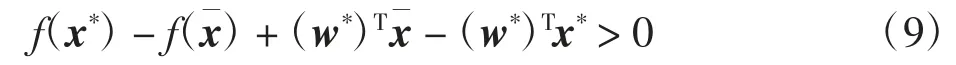
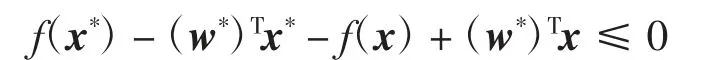
所以，对于x∈Rn，f（x）-（w*）Tx在x=x*取得最小值.

对任意x∈Rn，xTQx=xTM（Q）x，M（Q）是正定矩阵，因而当x=x*时，凸函数（x-Q）取最小值.所以x*和w*满足

假设存在v，使得（w*）T（v-v*）＜0.由式（8），对任意x∈Rn，有

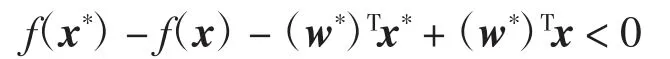
而当x=x*时上式不成立.所以，对任意v∈Ω，（w*）T（v-v*）≥0.根据投影定理，上式等价于

将v*=x*代入式（11）得

将式（10）代入式（12）得

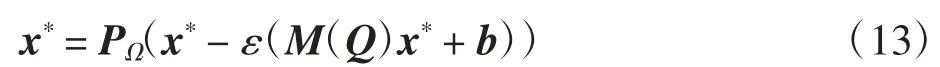
因此，由式（13）可给出问题（1）的比例时滞投影神经网络模型（2）.

综上，系统（2）的平衡点为问题（1）的解，当神经网络的平衡点稳定时，该平衡点为二次规划问题的最优解.

2 主要结果

定理1对任意φ（t）∈C（[qt0，t0]，Rn），系统（2）在[t0，+∞）上存在唯一的连续解x（t）.

证明设

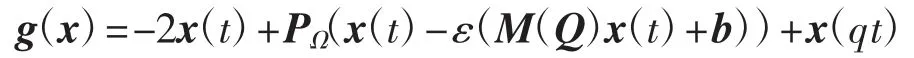
若φ、γ∈Rn同时为系统（2）的解，则有

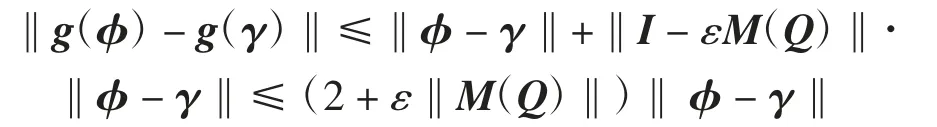
故g（x（t））在C（[qt0，t0]，Rn）上是Lipschitz连续的.从而对于φ（t）∈C（[qt0，t0]，Rn），系统（2）在[t0，T]上存在符合初始条件的唯一的连续解x（t）.

记x*为系统（2）的平衡点，则有

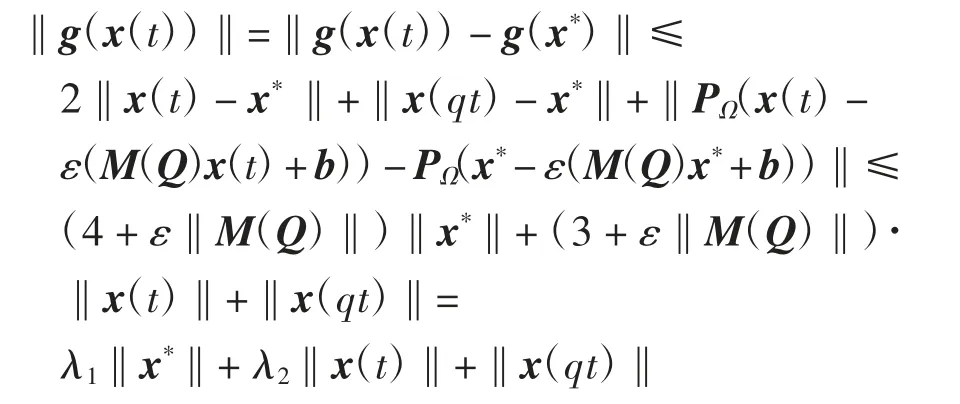
其中：λ1=4+ε‖M（Q）‖，λ2=3+ε‖M（Q）‖.

对任意t∈[t0，T]，有和x（t）=φ（t），t∈[qt0，t0]，从而有

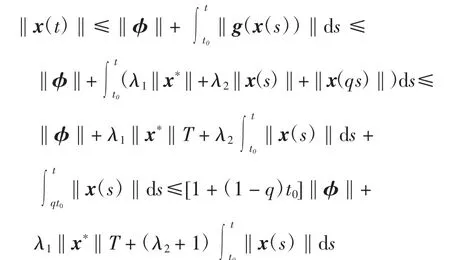
由引理2可得

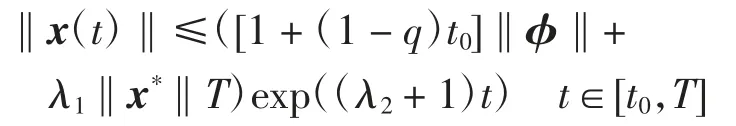
故x（t）在[t0，T]有界.根据引理4，系统（2）在[t0，+∞）存在连续解x（t）.定理证毕.

定理2若M（Q）是半正定的，则系统（2）的解x*是全局渐近稳定的.

证明设y（t）=x（et），求导得

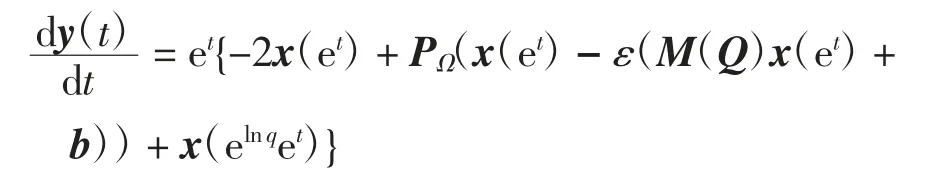
取τ=-lnq≥0，则系统（2）变换为

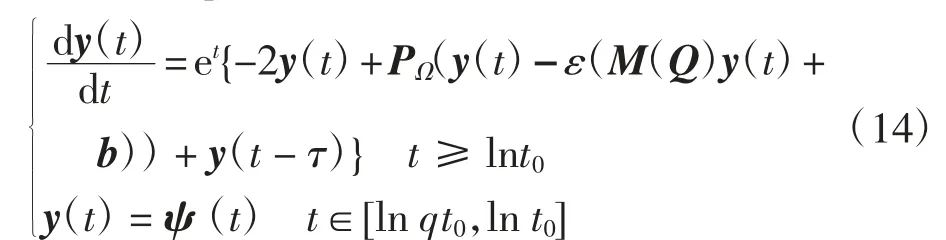
构造Lyapunov函数

其中：

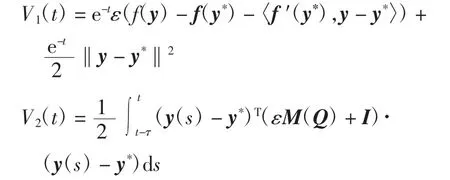
设y*为系统（14）的平衡点，容易验证y*=x*.

对V1（t）沿系统（14）的轨迹求导，得

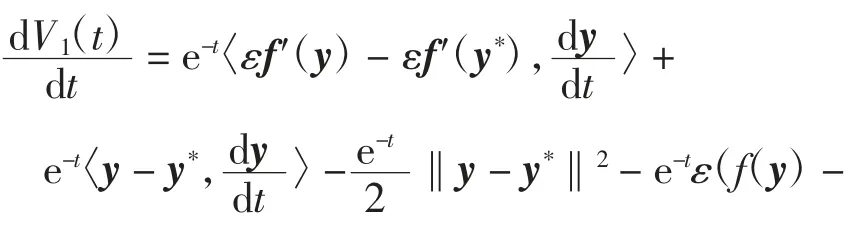
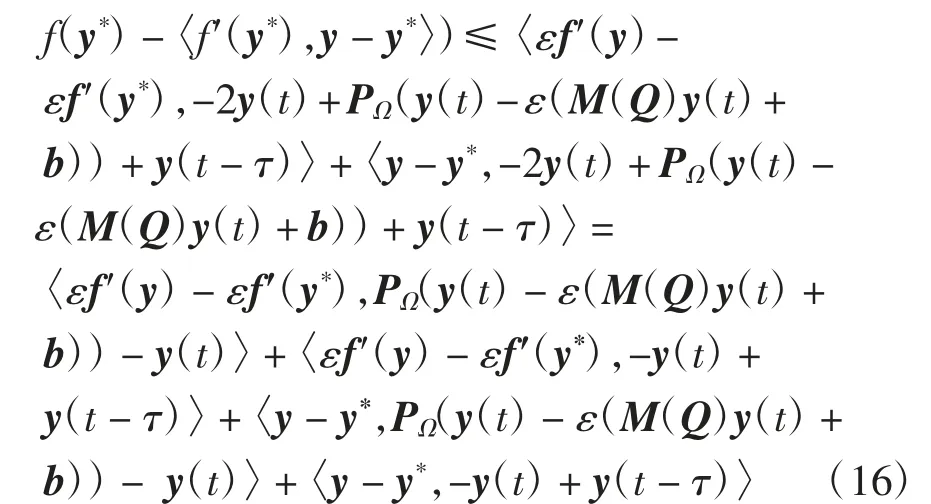
利用内积的性质可得

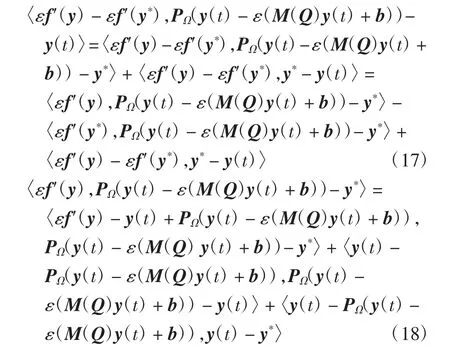
结合式（17）和式（18），利用引理4可得

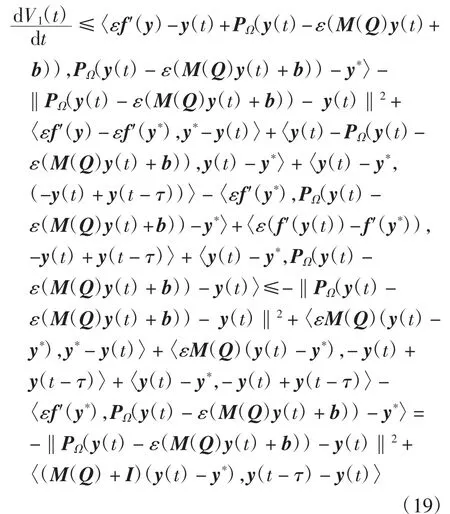
对V2（t）求导可得

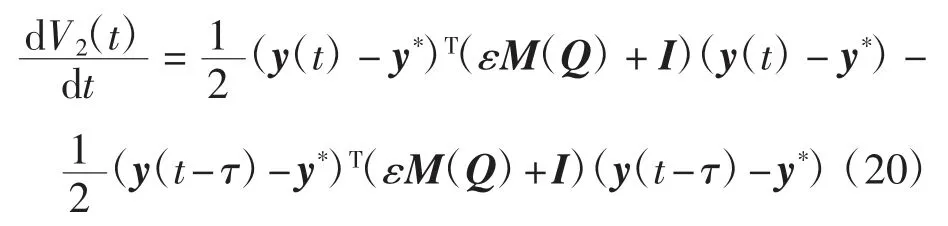
对式（15）求导，并将式（19）和式（20）代入，得

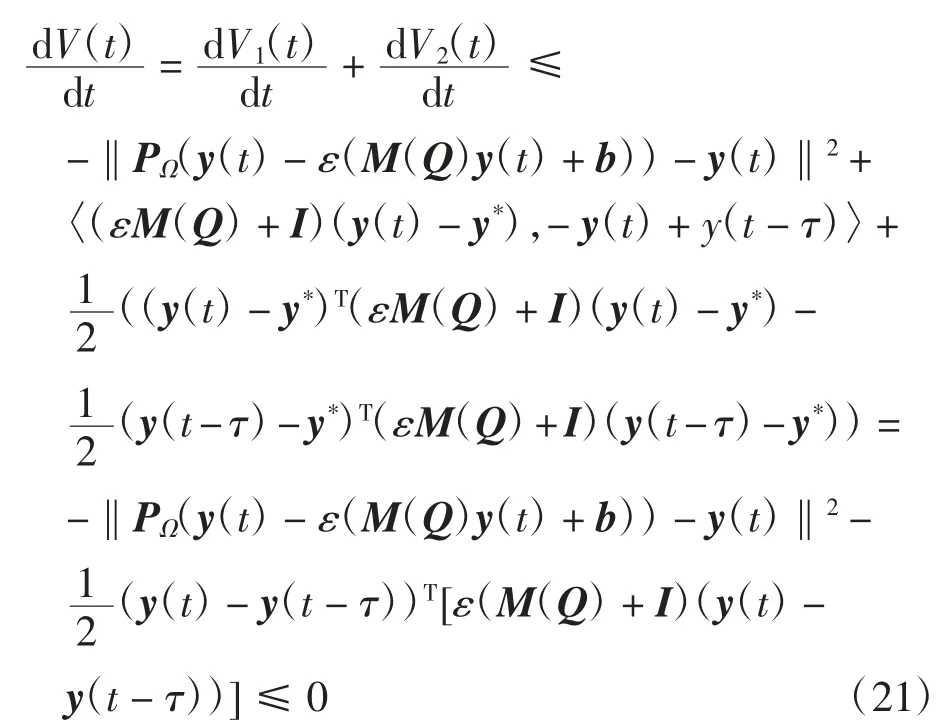
当且仅当y（t）=y*时，，此时x（t）=x*.由定义2知，系统（14）的解是渐近稳定的.当t→+∞时，‖y（t）‖→+∞，此时V（t）→+∞，又因为y（t）=x（et），则系统（2）的解是全局渐近稳定的，此时的平衡点就是二次规划问题（1）的全局最优解.定理证毕.

注2由式（13）可以给出问题（1）的形式更一般的比例时滞投影神经网络：

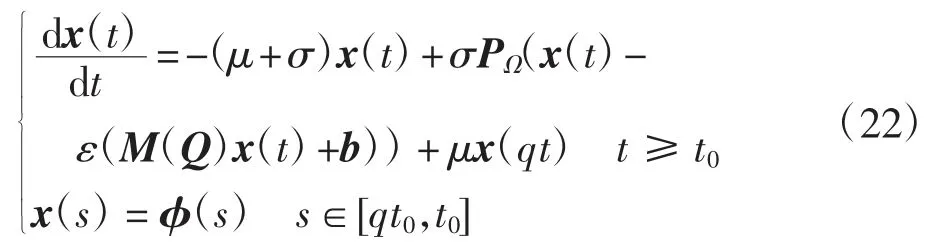
其中μ、σ均为正数.若M（Q）为半正定矩阵，则系统（22）是全局渐近稳定的.事实上，只需将定理2证明中的Lyapunov函数的V2（t）改为

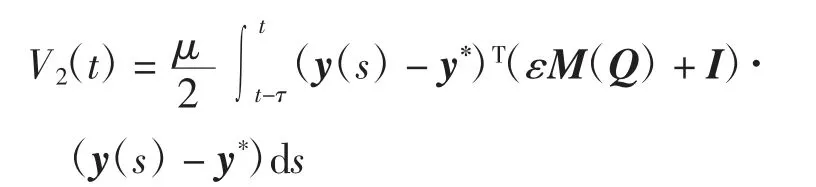
其余部分及证明过程同定理2一致.

注3在系统（2）中取q=1，或在系统（22）中取q=μ=σ=1，则得到无时滞投影神经网络：

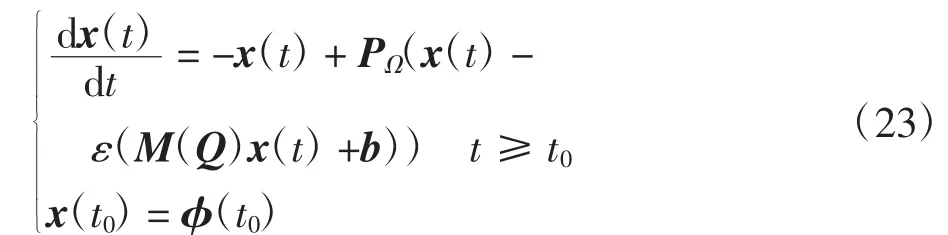
对于神经网络（23），本文的结论仍然成立.

3 数值算例及仿真

例1考虑二次规划问题：

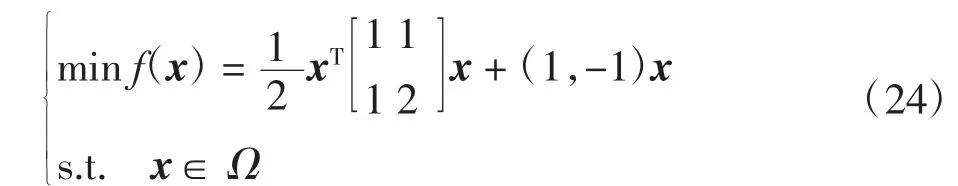
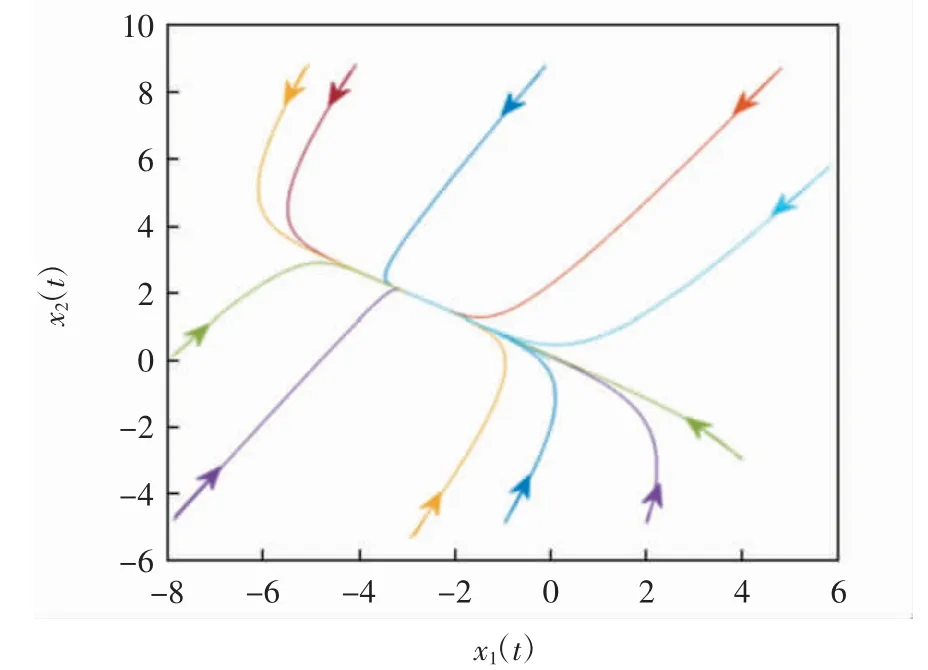
图1 问题（24）对应的比例时滞投影神经网络的相轨迹Fig.1 Phase trajectories of projection neural network with proportional delays corresponding to Problem（24）

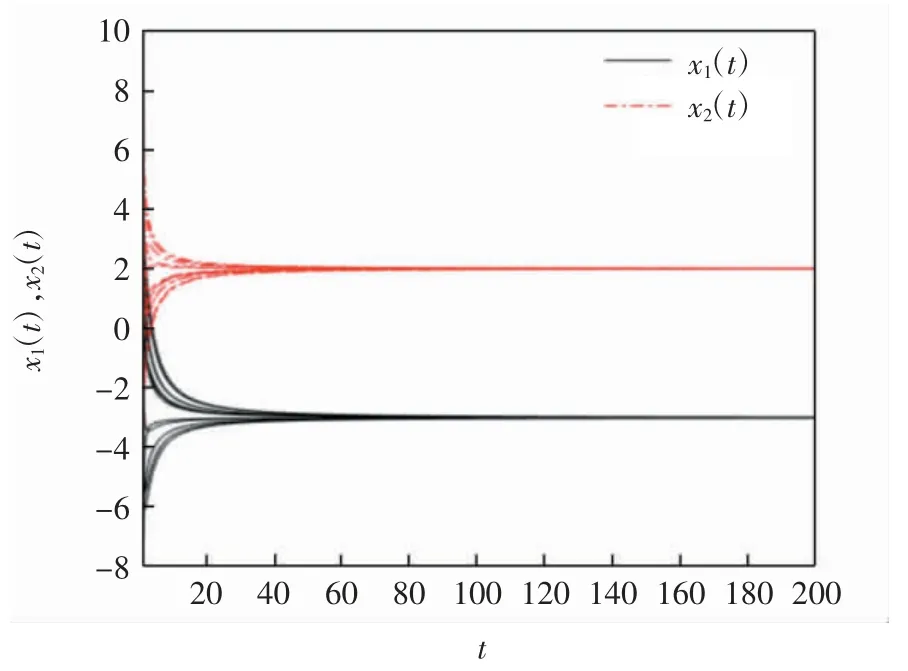
图2 问题（24）对应的比例时滞投影神经网络的时间响应曲线Fig.2 Time response curves of projection neural network with proportional delays corresponding to Problem（24）

例2考虑二次规划问题：

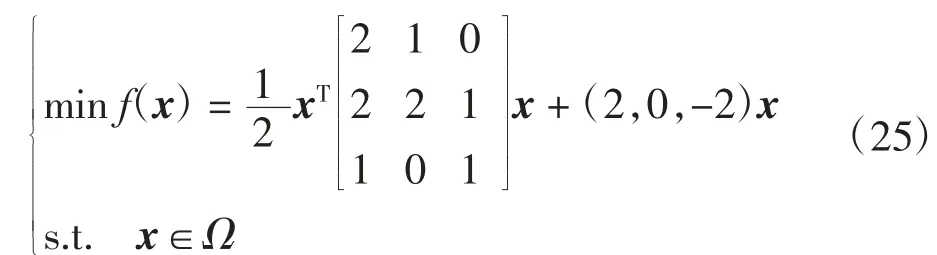
故M（Q）为正定矩阵，从而矩阵Q为亚正定矩阵，由定理2可知，二次规划问题（25）有唯一的最优解，该最优解为问题（25）对应的比例时滞投影神经网络（2）的平衡点x*=（-2.747 0，1.417 9，2.655 4）T，并且它是全局渐近稳定的.问题（25）对应的投影神经网络的相轨迹和时间响应曲线分别见图3和图4，可以看出，不同初值的解轨迹最终收敛到平衡点x*.

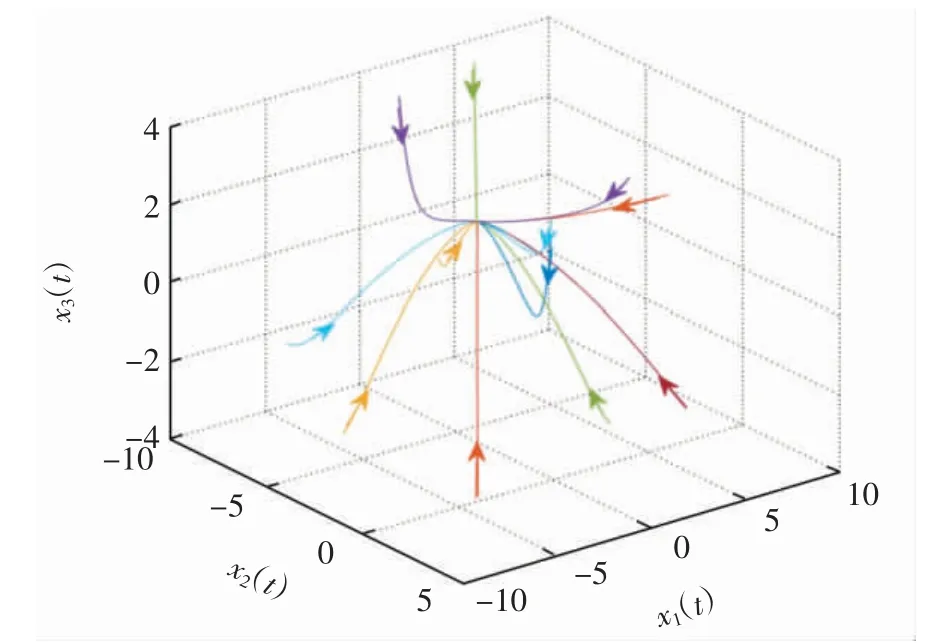
图3 问题（25）对应的比例时滞投影神经网络的相轨迹Fig.3 Phase trajectories of projection neural network with proportional delays corresponding to Problem（25）

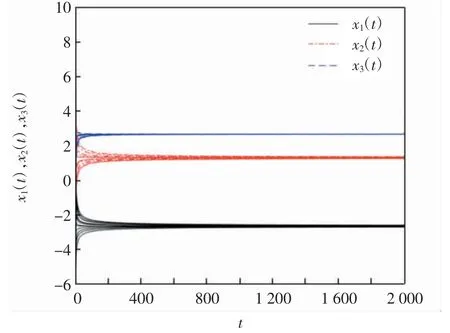
图4 问题（25）对应的比例时滞投影神经网络的时间响应曲线Fig.4 Time response curves of projection neural network with proportional delays corresponding to Problem（25）

4 结论

本文针对一类闭凸集上的二次规划问题，利用投影定理和Lagrange函数法构造比例时滞神经网络模型，说明了比例时滞神经网络的平衡点就是二次规划问题的最优解.基于变换后的系统构造Lyapunov泛函，证明了该网络在一定条件下是全局渐近稳定的.本文结果是对以往的凸二次规划问题的推广，并且给出了比例时滞神经网络模型平衡点和二次规划问题最优解的关系.最后通过数值算例及仿真验证了全局渐近稳定性准则的有效性.