小型降落伞充气和伞衣塌陷过程

张延泰，孙建红，2，侯 斌

（1.南京航空航天大学 飞行器环境控制与生命保障工业和信息化部重点实验室，南京 210016；2.南京航空航天大学民航学院，南京 210016）

马航370航班失联后，南京航空航天大学民机救生团队与中国商用飞机有限责任公司（中国商飞）针对民航客机联合研发了分离式应急记录跟踪系统，该系统又被称为报信者（harbinger，HBG）系统[1-4].在HBG系统中，应急飞行数据记录器（emergency flight data recorder，EFDR）在飞机坠毁前弹射离机.利用降落伞可以有效降低EFDR坠落速度，减小坠落冲击.降落伞离机后迅速开伞，其伞衣充气过程较为复杂[5]，而针对小型装置设计的降落伞不多，对其展开过程的研究相对较少，其中小型伞是否存在伞顶塌陷及其塌陷机理均缺乏细致研究.如果小型伞伞衣在充气阶段发生塌陷或扭曲变形，尽管是局部也可能会导致开伞失败.研究小型降落伞充气过程，分析伞衣附近的流场特性，判断其工作充气过程中的安全性对小型装置投放等工程应用具有重要意义.

降落伞在充气过程中，流体与伞衣的耦合作用具有非定常、柔性大变形等非线性特性，是流固耦合研究的难点之一.降落伞充气过程的理论模型最早出现于1927年，是后续降落伞充气过程计算方法的基础.在此基础上，Mohaghegh等[6]研究了降落伞的充气过程，发现充气时间与伞型、伞口面积和来流速度等因素相关.这些充气模型多用于计算充气时间和开伞动载，没有考虑伞衣局部变形等问题.Wolf等[7]研究了群伞的充气过程，发现减速伞充满后发生塌陷会严重影响伞衣的减速效果.随后，NASA在猎户座计划中[8]发现伞衣在充气过程中存在过度充气和部分塌陷的问题.在实验的基础上，Yavuz[9]针对物伞系统和伞衣尾流区速度分布建立了理论模型.彭勇等[10]基于流体连续方程和动量方程，提出了降落伞充气过程的尾流再附动力学模型.在试验与仿真结合的研究中，王海涛[11]研究了大型降落伞充气过程中的伞衣变形和抽打现象，分析了抽打现象的特点和形成原因.

此外，利用实验和数值模拟技术可以进一步分析伞衣附近流场特性对伞衣变形的影响.Johari等[12]采用PIV和水洞试验技术研究了降落伞的尾流场，认为涡脱落对伞衣背部有周期性的吸力作用.Fang等[13]采用数值模拟方法研究了十字伞的充气过程，对比分析了单伞和双伞系统，讨论了伞衣附近流场特性对伞衣充气过程的影响.孙建红等[14]针对阻力伞实验中的非定常运动和尾流干扰，结合理论分析和数值模拟技术，分析了附加质量模型，建立了伞衣阻力系数的修正方法，并与实验结果进行了对比分析.

综上所述，研究人员在较早的工程应用中发现并讨论了尾流再附与伞衣塌陷等问题，但研究主要关注伞衣投影直径、充气时间和开伞载荷的变化.针对小型降落伞的流场特性与伞衣变形相互作用的研究相对较少.本研究对小型降落伞的充气和伞衣塌陷过程进行数值模拟，分析了伞衣充气过程中流场特性和伞衣变形的演化规律，研究了来流速度和前置体质量对伞衣充气过程的影响，以期给出伞衣安全充气的工况范围.

1 数值计算方法

降落伞的充气过程是柔性体大变形流固耦合问题，可采用ALE方法进行数值模拟，通过罚函数方法进行流固耦合计算.根据美国国家运输安全委员会（national transportation safety board，NTSB）的事故报告，本研究工况中，设置HBG系统降落伞的开伞速度区间为40～160 m/s，可压缩流体控制方程为

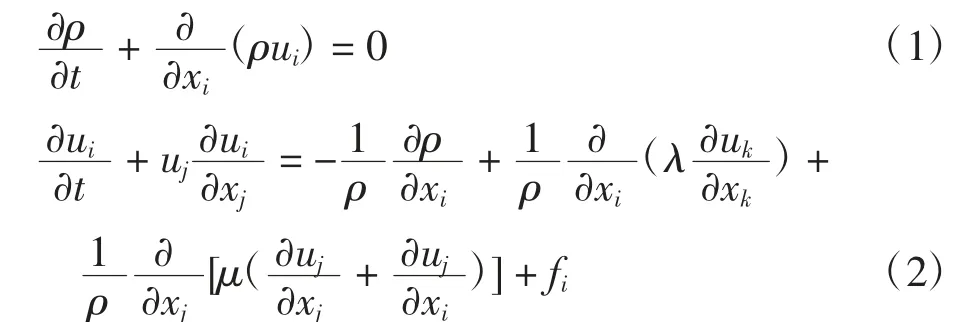
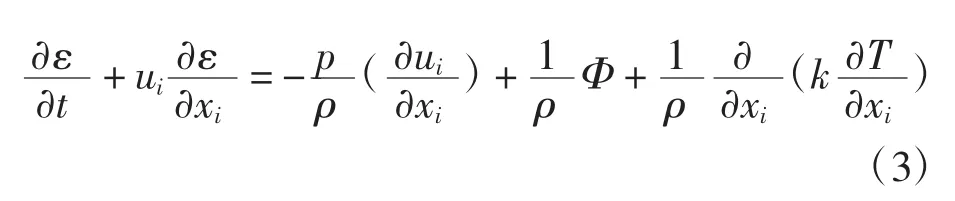
式（1）～式（3）中：t为时间；ρ为流体密度；ui为流体速度张量；p为流体压力；fi为体积力张量；ε为流体比内能；Φ为耗散函数；T为流体温度.

由于ALE方法在欧拉和拉格朗日坐标之外引入了参考坐标，所以在ALE方法中，材料域的节点信息需要被映射到空间域内，其流场变量的输运方程为

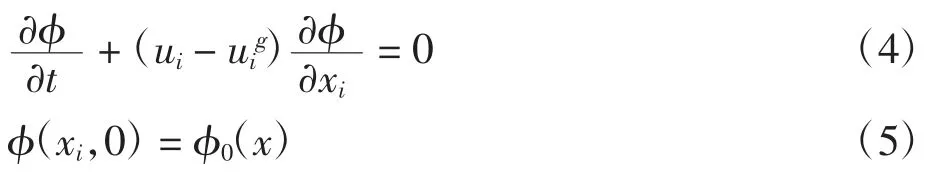
式（4）和式（5）中：φ为流场变量；φ0为当前时间步流场变量的初始值；uig为材料速度张量，当uig=0时对应欧拉方法，当uig=ui时对应拉格朗日方法.该数值模拟方法在本课题组前期研究中用于分析降落伞和阻力伞的充气过程[5，15].因此，有理由认为该数值模拟方法适用于本研究.

2 计算模型

HBG系统的降落伞为平面圆形伞，伞衣名义直径为1.9 m.根据平面圆形伞的折叠方法，伞衣首先按照伞衣幅做“平折叠”，随后做“Z字形”折叠，最后放入伞包.在数值模拟中采用类似真实平面圆形伞折叠的方法进行建模，图1为伞衣折叠前后的面积变化和折叠后的伞衣网格.由于降落伞挂载的电子设备体积较小，所以计算模型中将前置体简化为1个质点.计算域尺寸为6D0×6D0×15D0，在伞衣充气区域进行局部加密，总网格数约为2.6×106个，为保证质量守恒，计算域边界采用速度入口.

图1 数值模拟中的降落伞折叠模型Fig.1 Parachute folding model in numerical simulation

3 结果与分析

3.1 流场分析

由于大型降落伞充气过程中的剧烈变形可能导致伞衣破损或开伞失败[16]，而HBG系统的电子设备质量较小，因此可采用小型降落伞完成缓降功能.小型降落伞的刚度较大，其开伞过程与大型降落伞存在明显区别.为了阐明HBG系统小型降落伞的充气过程，首先以来流速度为100 m/s、电子设备质量为4 kg的工况为代表，研究伞衣充气过程的流场特性.

研究表明，伞衣外形变化与剪切层和近尾迹区涡结构等的演化密切相关[14].图2为来流速度为100 m/s时，伞衣充气过程的外形变化与压力云图，采用速度等值线的方法描绘出剪切层的位置和形态.

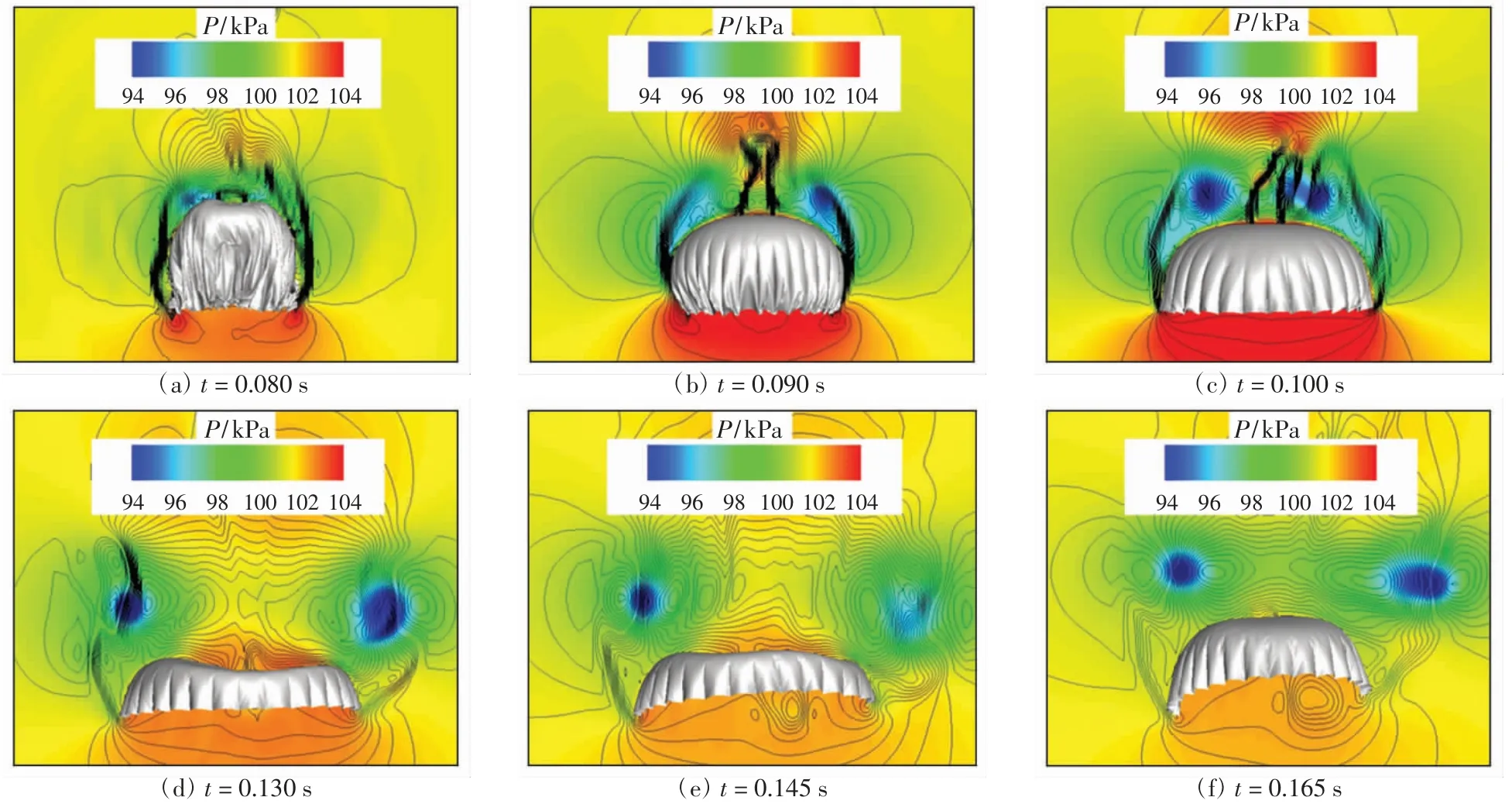
图2 伞衣对称面的压力云图Fig.2 Pressure contour of symmetrical plane of parachute

由图2（a）可以看出，当伞衣呈“灯泡”状时，剪切层在伞衣底边形成并紧贴于伞衣侧面.当剪切层发展到伞衣肩部时，伞衣发生分离并迅速失稳（图2（a））.随着伞衣扩张，剪切层的分离点逐渐向伞衣底边移动（图2（a）～图2（d））.同时，剪切层失稳后卷起的尾涡也在向伞衣外侧移动.在尾涡由中心向外侧移动时，伞衣顶部出现了高压区（图2（d）），说明伞衣在充气过程中出现了尾流再附现象.尾流再附造成伞衣在伞顶孔附近出现非对称的局部塌陷，加剧了伞衣近尾迹区流场的非对称特性，导致伞衣沿径向发生偏转（图2（f））.

为了进一步研究伞衣充气过程中流场演化的动力学特征，采用Lamb矢量散度描述伞衣附近流场特性[15].Lamb矢量散度定义为Δ·L，其中L=ω×u为Lamb矢量，ω为伪涡矢量，u为流体速度矢量.图3为流向速度为100 m/s时利用Δ·L描述的流场拓扑结构.由图3（a）～图3（c）可知，在伞衣侧面的剪切层中，Δ·L出现了明显的正负双层结构.该结构的动力学过程包含了强应变率区和涡量区间的相互作用[15].尾流再附发生后，伞衣侧面的Δ·L双层结构演化为正负交替结构（图3（d）～图3（f））.该正负交替结构一般出现在钝头体绕流的近尾迹区中，说明此时剪切层在伞衣底边形成后不能稳定地向下游发展，而是会迅速失稳.这种流场演化现象与无限质量充气过程明显不同.在无限质量充气过程中，当伞衣投影面积达到峰值后，剪切层和尾涡会进入周期性演化[17].而在HBG系统小型降落伞的有限质量充气过程中，伞衣侧面剪切层不会进入周期性演化，而是出现剧烈的涡运动和流体拉伸变形运动.

图3 伞衣对称面Lamb矢量的散度云图Fig.3 Lamb vector divergence contour of symmetrical plane of parachute

HBG系统的降落伞具有前置体质量小、伞衣面积小的特点，其开伞过程属于有限质量充气.Desabrais[17]从流场特性演化的角度将降落伞充气过程划分为3个阶段.与Desabrais[17]研究的无限质量充气过程相比，HBG系统降落伞充气过程前2个阶段的流场特性和伞衣外形变化特征是非常相似的.而在无限质量充气的第3个阶段，伞衣侧面的剪切层开始周期性演化，伞衣产生周期性的“呼吸”现象.与此不同，HBG系统降落伞在第3阶段出现了尾流再附，导致降落伞在充气过程的后2个阶段中，剪切层不会进入周期性演化，流场的非对称特性也比无限质量充气更明显.

图4为流向速度为100 m/s时，HBG系统降落伞充气过程中动载和伞衣投影面积的变化曲线.

图4 伞衣充气过程中的动载与投影面积Fig.4 Load and projected area of parachute during inflation

由图4可以看出，根据流场演化的特点，充气过程可以被分为4个阶段.第1个阶段为0～0.060 s，伞绳和伞衣从折叠状态拉直，伞绳的拉直力使动载出现第1个峰值；第2个阶段为0.060～0.080 s，伞衣底边首先开始充气扩张，随着气流进入伞衣并在伞顶聚集形成高压区，伞衣顶部开始扩张出现“灯泡”状；第3个阶段为0.080～0.130 s，此阶段内伞衣投影面积迅速增大，开伞动载出现峰值，随后由于尾流再附，伞衣顶部出现局部塌陷；第4个阶段为0.130～0.165 s，伞衣从伞顶局部塌陷的状态逐渐回弹，在非对称流场的影响下，伞衣在沿轴向运动的同时沿径向发生偏转.在大型降落伞的空投实验中，伞顶在塌陷后的回弹过程中，可能发生伞衣缠绕造成严重破损[11].由于HBG系统降落伞尺寸较小，虽然伞顶在充气过程中发生了塌陷和回弹，但并没有缠绕其他部分伞衣.

3.2 前置体质量和来流速度对降落伞充气过程的影响

由前文分析可知，在典型工况下，HBG系统的小型降落伞在回弹过程中不会发生伞衣缠绕.为了进一步分析该小型降落伞在充气过程中的安全性，需要给出前置体质量和来流速度等因素对伞衣充气过程的影响.根据环缝伞相关研究[18]可知，尾流再附现象与物伞系统的质量比和速度比相关，质量比和速度比分别为

式（6）和式（7）中：m为前置体质量；ρ为流体密度；D0为伞衣名义直径；U∞为来流速度；UF为缓降速度.

现役飞行数据记录器质量约为6～12 kg，在HBG系统中，离机缓降的电子设备质量小于传统飞行数据记录器.电子设备在飞机坠毁前弹射离机，假设来流密度为1.225 kg/m3不变，当来流速度为100 m/s（UR=0.5）、伞衣名义直径为1.9 m时，改变电子设备质量，分别取质量比为0.2、0.5、0.8、1.1和1.4的工况进行分析.图5为流向速度U∞=100 m/s、不同质量比RN时，伞衣在充气过程第3和第4阶段内的外形变化.

图5 不同质量比时，伞衣充气过程中的外形变化Fig.5 Shape change of parachute during inflation with different mass ratio

由图5可以看出，在0～0.120 s的时间内，不同质量比工况下，伞衣外形的变化规律相近.在伞衣充气过程的第3阶段，均出现了伞顶的局部塌陷.当RM=0.2时，顶部局部塌陷后，伞衣塌陷的范围逐渐变大，最终导致全部伞衣剧烈变形.当RM=1.4时，顶部局部塌陷后，伞衣回弹，没有出现伞衣完全塌陷的现象.

流向速度U∞=100 m/s时，开伞过程中的伞衣投影面积如图6所示.

图6 质量比对伞衣投影面积的影响Fig.6 Effect of mass ratio on projected area of parachute

开伞过程的前0.070 s是伞衣伞绳的拉直过程，由于伞衣底面充气口面积较小，伞衣充气速度较慢，导致伞衣投影面积变化较小.随后伞衣充气过程进入第2个阶段，大量空气冲入伞衣，造成伞衣投影面积迅速增加.在充气过程的最后阶段，当RM=0.2时，伞衣大面积塌陷使其投影面积明显大于其他工况.由图6可以看出，当RM=0.2时，伞衣投影面积峰值明显大于其他工况.当RM=0.5～1.4时，伞衣投影面积的变化曲线相近，说明在0.5＜RM＜1.4工况中，不会由于尾流再附导致伞衣大面积塌陷，是较为安全的工况.

为了进一步说明前置体质量不同时，伞衣充气过程的流场特性，图7给出了流向速度U∞=100 m/s时，伞衣充气过程第3和第4阶段典型时刻的压力云图.由图7可以看出，t=0.100 s时伞衣附近流场特性相近，剪切层在伞衣底边形成后向下游发展.在伞衣的近尾迹区中，剪切层失稳并卷起旋涡.随着伞衣充气过程向第4阶段发展，伞衣附近流场区别越来越明显.在RM=0.2的工况中，由于前置体质量较小，在降落伞气动力作用下，前置体向伞衣方向回弹，导致t=0.140 s时部分伞绳处于松弛状态（图7（a））.由于伞绳对伞衣的拉扯作用减小，伞衣难以保持类似半球壳状的外形.对比RM=1.4、t=0.140 s时伞衣对称面的压力云图（图7（b））可以发现，RM=0.2时伞前气体的高压区域几乎消失，说明此时伞衣对于来流气体的滞止效应非常微弱.

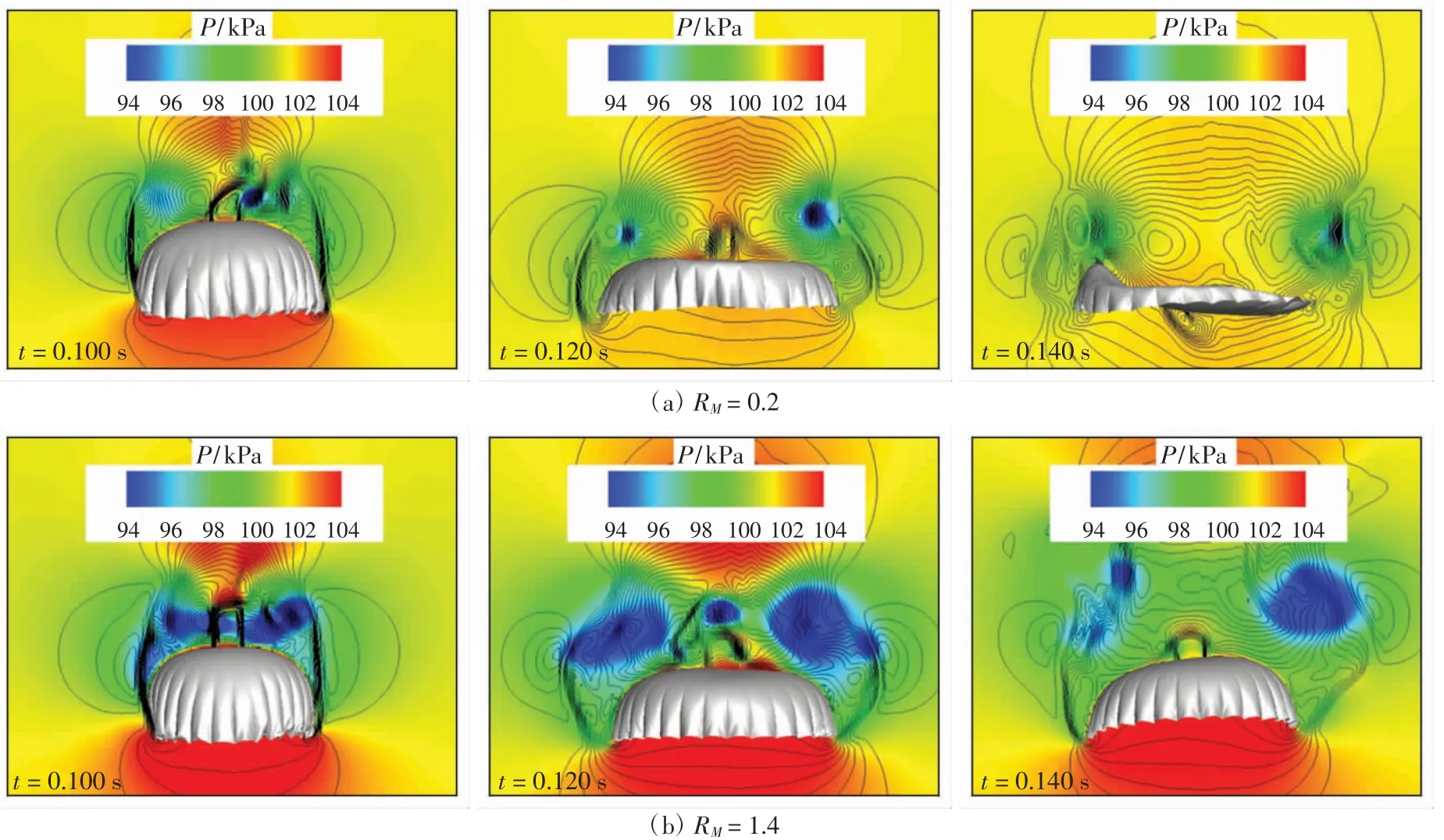
图7 不同质量比伞衣对称面的压力云图Fig.7 Pressure contour of symmetrical plane of parachute with different mass ratio

本研究中来流速度为40～160 m/s，缓降速度为8 m/s，当前置体质量为4 kg（RM=0.5）时，分别取速度比RV为5.00、8.75、12.50、16.25和20.00的工况进行分析.图8中给出了速度比RV为5.00和20.00的工况下，伞衣在充气过程第3和第4阶段的外形变化情况.图9进一步给出了速度比RV为5.00、8.75、12.50、16.25和20.00的工况下，开伞过程中的动载和伞衣投影面积变化曲线.

图8 不同速度比时，伞衣充气过程中的外形变化Fig.8 Shape change of parachute during inflation in different speed ratio

由图8可以看出，在不同速度比的工况下，伞衣在充气过程中均经历了由充满到伞顶塌陷再到伞顶回弹的外形变化过程.在伞衣充气时，没有出现伞衣完全塌陷的现象.为了方便对比分析，将动载峰值时刻定义为伞衣充满时间，采用无量纲时间t/tf绘制伞衣投影面积变化曲线（图9（b））.由图9（a）可以看到，伞衣充气时间随着来流速度的增加而降低，同时动载峰值随着来流速度的增加而上升.由图9（b）可知，速度比不同时，伞衣投影面积的变化较为相似，说明在RM=0.5、5.00＜RV＜20.00工况下，伞衣在充气过程中均未出现大范围的伞衣塌陷现象，是较为安全的工况.

图9 速度比对开伞动载和伞衣投影面积的影响Fig.9 Effect of speed ratio on opening load and projected area of parachute

4 结论

本文采用任意拉格朗日-欧拉（ALE）方法数值模拟了HBG系统降落伞的充气过程，分析了伞衣充气过程的流场特性，研究了前置体质量和来流速度对伞衣塌陷的影响，研究结果表明：

（1）根据流场演化的特点，伞衣的充气过程可分为4个阶段.其中，前2个阶段的流场特性和伞衣外形变化特征与无限质量充气过程非常相似.在充气过程的后2个阶段，剪切层不会进入周期性演化，流场的非对称特性也比无限质量充气更明显.

（2）伞衣在充气过程中出现尾流再附，并导致伞顶局部塌陷.若前置体质量过小，伞衣塌陷的范围会逐渐变大，并最终导致全部伞衣剧烈变形，是较为危险的工况.当0.5＜RM＜1.4时，伞衣顶部局部塌陷后伞衣回弹，不会由于尾流再附导致伞衣大面积塌陷，开伞失败的风险较小，是较为安全的工况.

（3）在较大的工况范围内，当来流速度不同时，伞衣投影面积的变化规律较为相似.当5.00＜RV＜20.00时，伞衣在充气过程中均未出现大范围的伞衣塌陷现象，开伞失败的风险较小，是较为安全的工况.