一类可积系统在n次多项式扰动下Abel积分孤立零点个数的估计
2022-10-15王逸凡李宝毅张永康隋世友
王逸凡,李宝毅,张永康,隋世友
(1.天津师范大学数学科学学院,天津 300387;2.天津商业大学理学院,天津 300134)
1 引言和主要结果
Hamilton系统在n次多项式扰动下Abel积分I(h)孤立零点个数的估计即为弱化希尔伯特第十六问题[1-2],是常微分方程定性理论的研究热点之一.文献[3-4]首先证明了I(h)的孤立零点个数存在一致的上界,但并没有得到确切的表达式.随后关于该问题的研究主要集中在2个方面,一方面是讨论低次Hamilton系统在低次扰动下I(h)的孤立零点个数,另一方面是估计超椭圆Hamilton系统在n次多项式扰动下I(h)的孤立零点个数.
随着研究的深入,许多学者开始关注可积系统在多项式扰动下的分岔现象.文献[11]研究了可积系统(x˙,y˙)=(y(1+x),-x2k-(11+x))在n次多项式扰动下的分岔现象,得到了系统极限环个数的上确界.文献[12]研究了可积系统(x˙,y˙)=(-y(x-a)m1(y-b)m2,x(xa)m1(y-b)m2)在n次多项式扰动下I(h)的孤立零点个数,其中ab≠0且m1、m2∈N.文献[13]研究了可积系统(x˙,y˙)=(-y(x2+a2)m,x(x2+a2)m)在n次多项式扰动下的极限环个数,其中a≠0且m∈N.
本文考虑扰动的可积系统
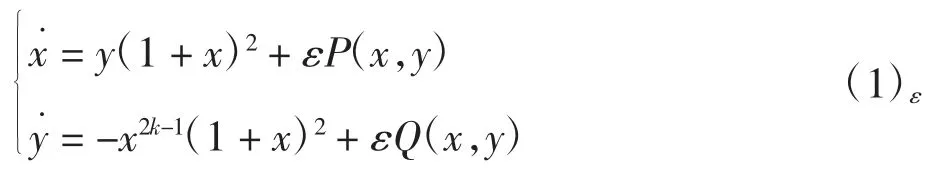
其中:k∈N+,P(x,y)、Q(x,y)为n次多项式.系统(1)0存在顺时针走向的周期闭轨族
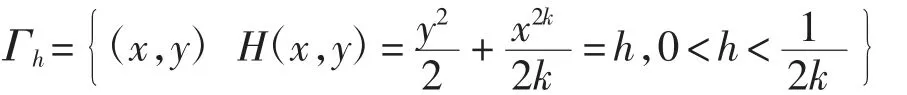
设Γh与x正、负半轴交于Ah+=(ak(h),0)、Ah-=(-a(kh),0),其中
记Abel积分

的孤立零点个数的上确界为Z(n,k).
定理对于扰动系统(1)ε,当I(h)≢0时,Z(n,1)=n,Z(n,2)≤n+2[n/2]+7,Z(n,k)≤n+(2k-1)·[n/2]+4k+1(k≥3).
2 Abel积分的计算
引理1当i、m、r∈N时,有
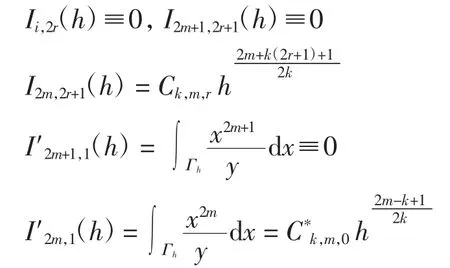
其中:Ck,m,r、C*k,m,0∈R+
证明由Γh关于x轴对称可知Ii,2r(h)≡0.由首次积分可知,周期闭轨Γh对应y=y±(x,h)=,即
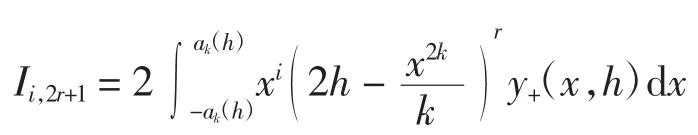
因此,由Γh关于y轴对称可知I2m+1,2r+1(h)≡0.
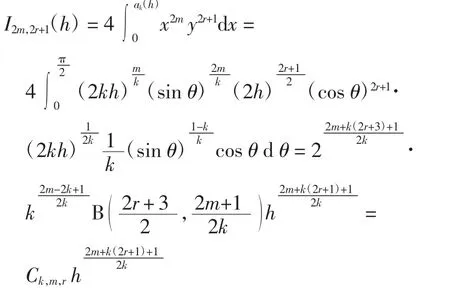

引理2设m∈N,则有
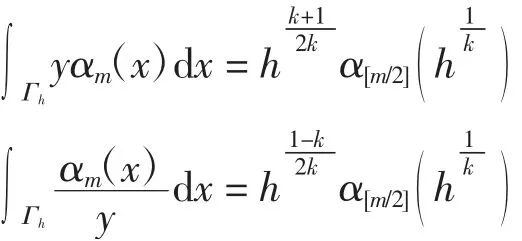
证明结合引理1可得

同理可得
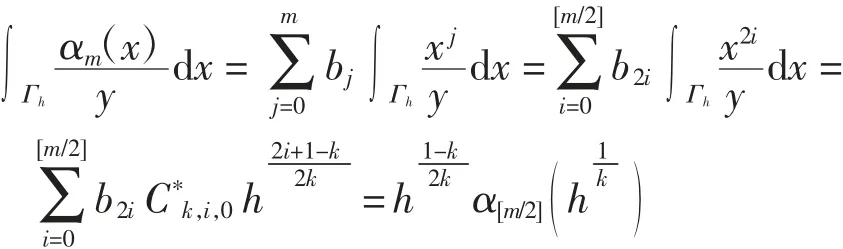
引理证毕.
引理3
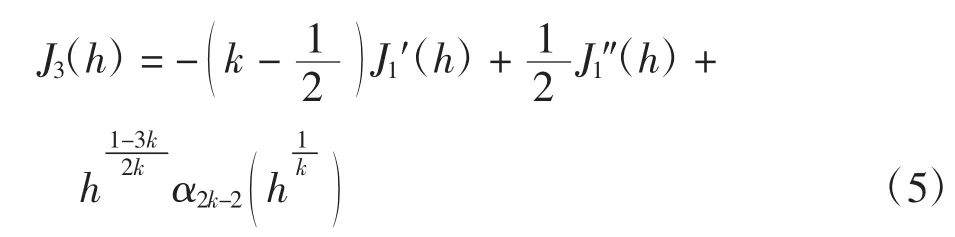
证明结合引理1可得
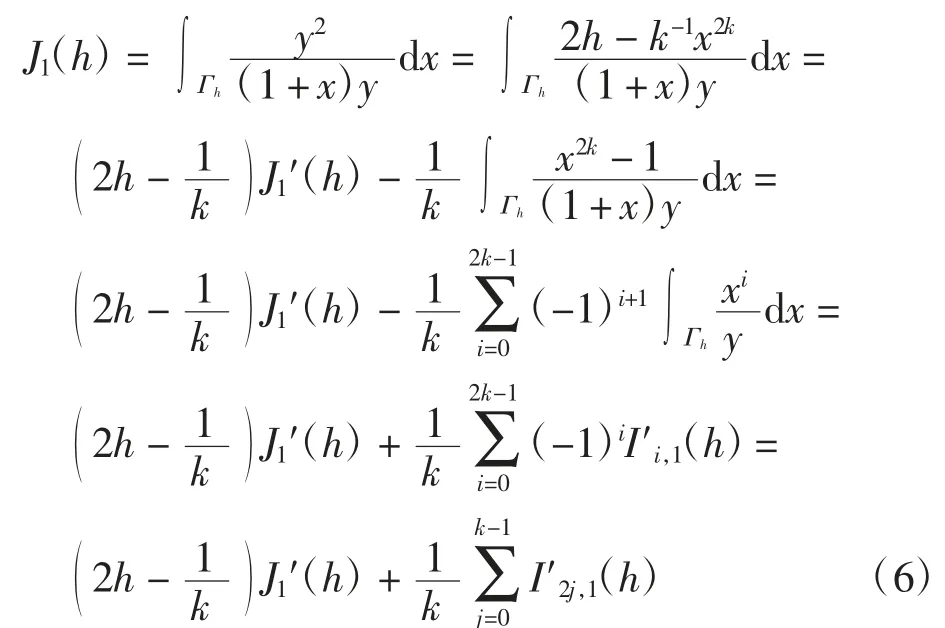
进而有
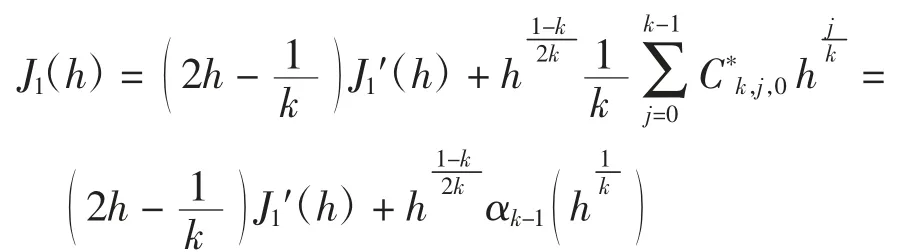
由首次积分可得,在Γh上有,结合引理2可得
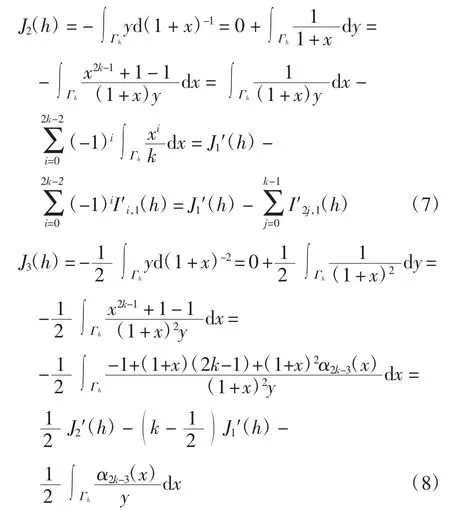
从而
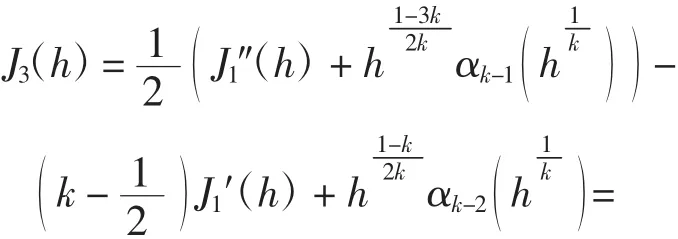
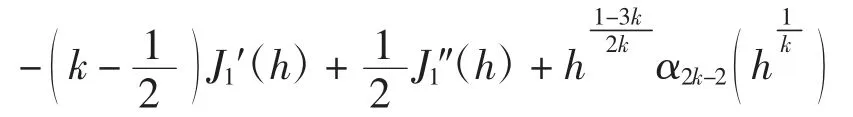
引理证毕.
引理4当k=1时,记则有
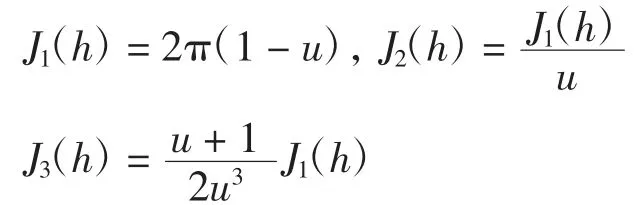
证明在式(3)中令k=1,则有
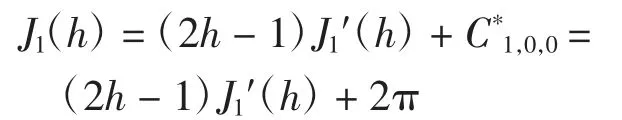

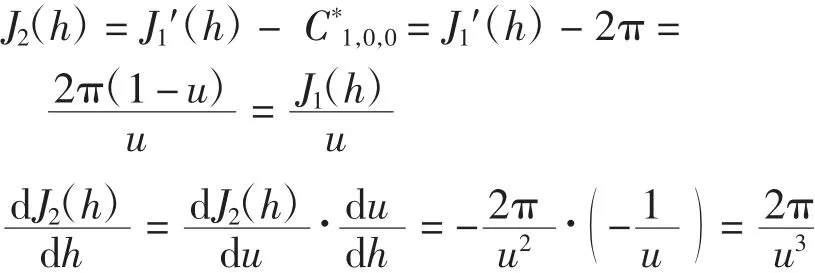
结合式(8)可得
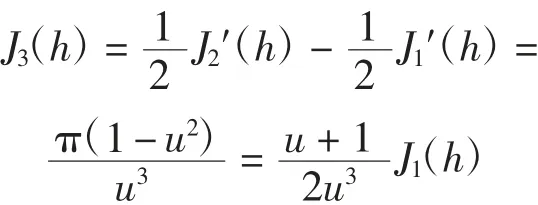
引理证毕.
引理5当时,系统(1)ε的Abel积分为
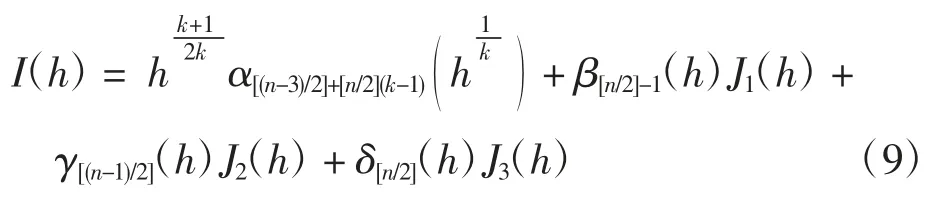
证明计算得
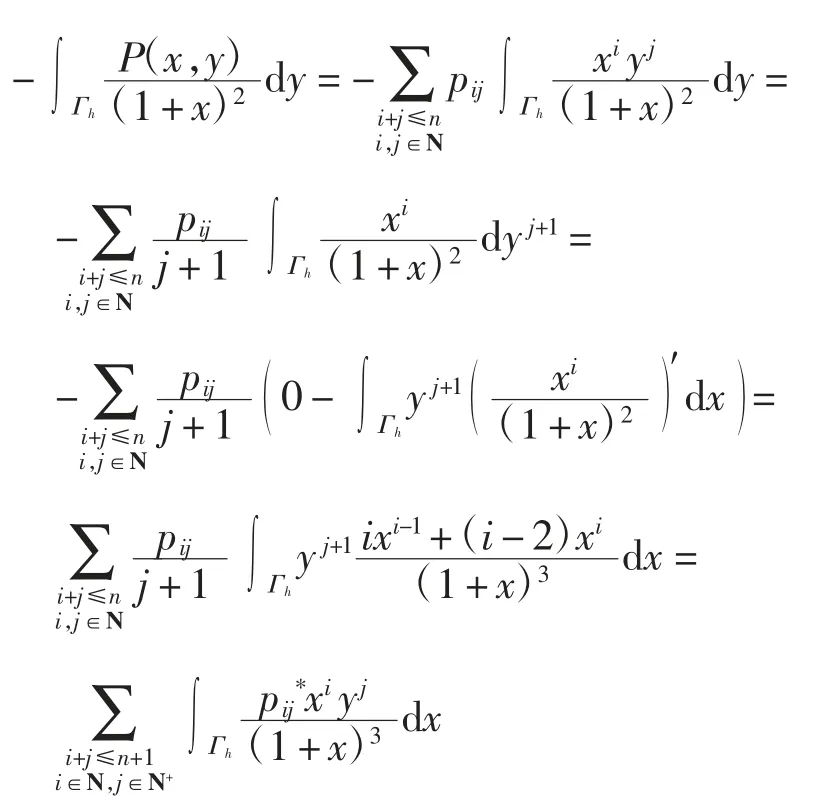
定义

由Γh关于x轴对称可得,当j为偶数时,

αn+2[n/2](k-1)-2kl(x)可表示为

α″n+2[n/2](k-1)-2kl(-1)≠0的必要条件为

α′n+2[n/2](k-1)-2kl(-1)≠0的必要条件为

则结合引理2可得

引理证毕.
将引理3的结论代入式(9)可得

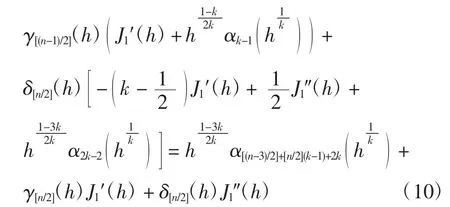
对式(3)关于h求导可得
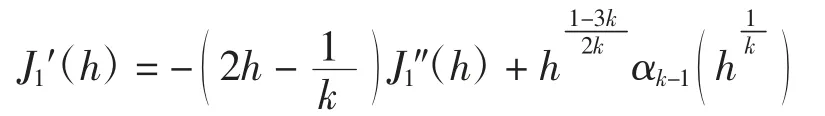
代入式(10)可得
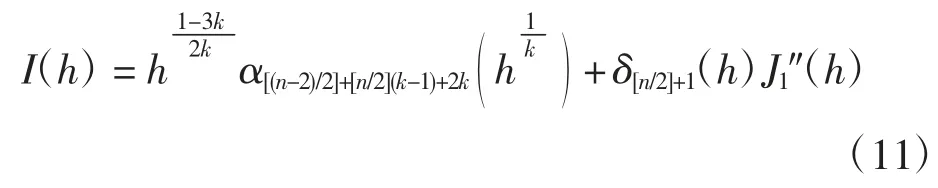
3 Abel积分孤立零点个数的估计
引理6[14]实系数多项式f(x)=cmxm+cm-1xm-1+…+c1x+c0的正零点个数等于f(x)的系数列cm,cm-1,…,c1,c0的变号次数或者变号次数减去某个正偶数.
引理7[15]设φ(ih)为)上的连续函数,且当0<h≪1时,φi(h)=ηihsi+o(hsi),其中:ηi≠0,1≤i≤m且s1<s2<…<sm,则存在实数e1,e2,…,em,使得在)上至少存在m-1个正变号零点.
引理8[15]设A(h)和B(h)在开区间(a,b)分别有u*和v*个零点(计重数),若系统P(h)=B(h)满足条件:
(1)P(h)在闭区间[a,b]连续,在开区间(a,b)可导.
(2)A(h)和B(h)在闭区间[a,b]连续,F(h,P)在[a,b]×[lp,Lp]连续,其中[lp,Lp]为P(h)在[a,b]的值域.
则函数P(h)在开区间(a,b)至多有u*+v*+1个孤立零点(计重数).
定理的证明:
情况1当k=1时,结合引理4和引理5可得,若n=0,则
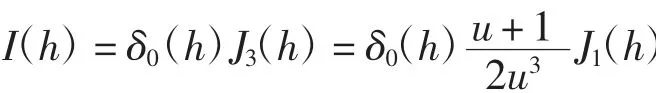
显然I(h)没有孤立零点,即Z(0,1)=0.
若n=1,则
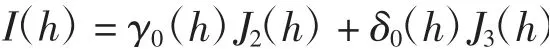
若n=2,则
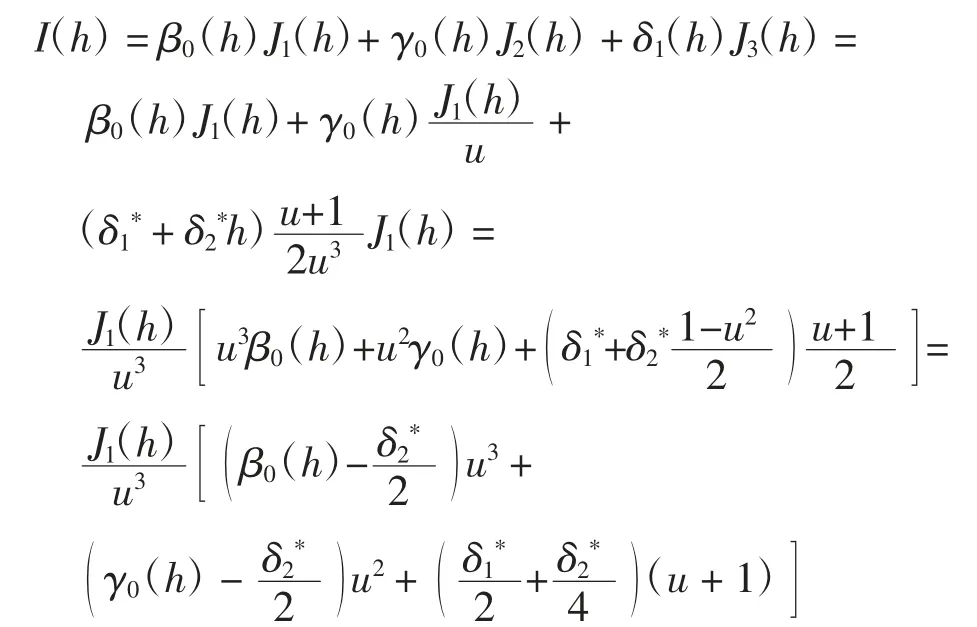
若n≥3,则
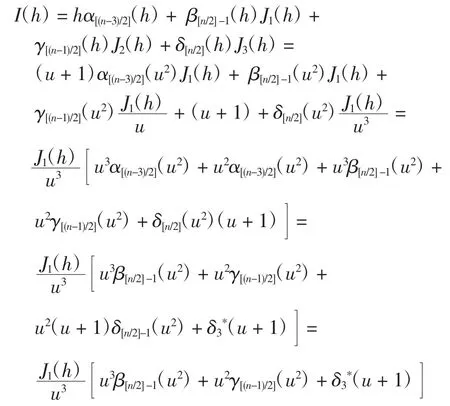
下面说明存在n次多项式P(x,y)和Q(x,y),使得(Ih)在至少有n个正变号零点.在系统(1)ε中取

结合式(2)和引理4可得
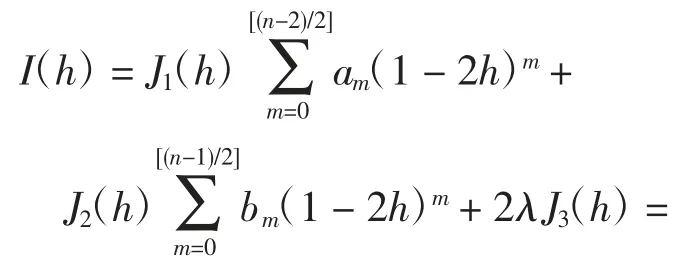
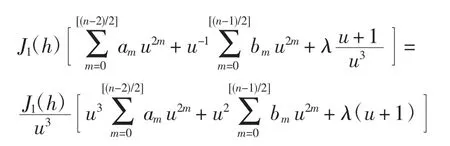
利用引理7可得,存在a0,a1,…,a[(n-2)/2],b0,b1,…,b[(n-1)/2],λ,使得在u∈(0,1)至少有n个正变号零点.综上,Z(n,1)=n.
情况2当k=2时利用式(7)和式(3)可得
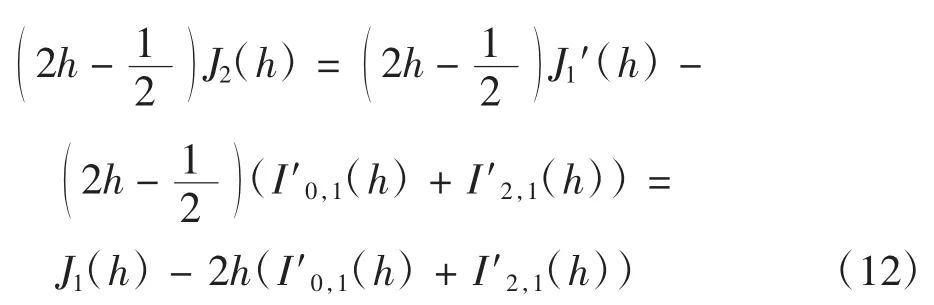
同时有
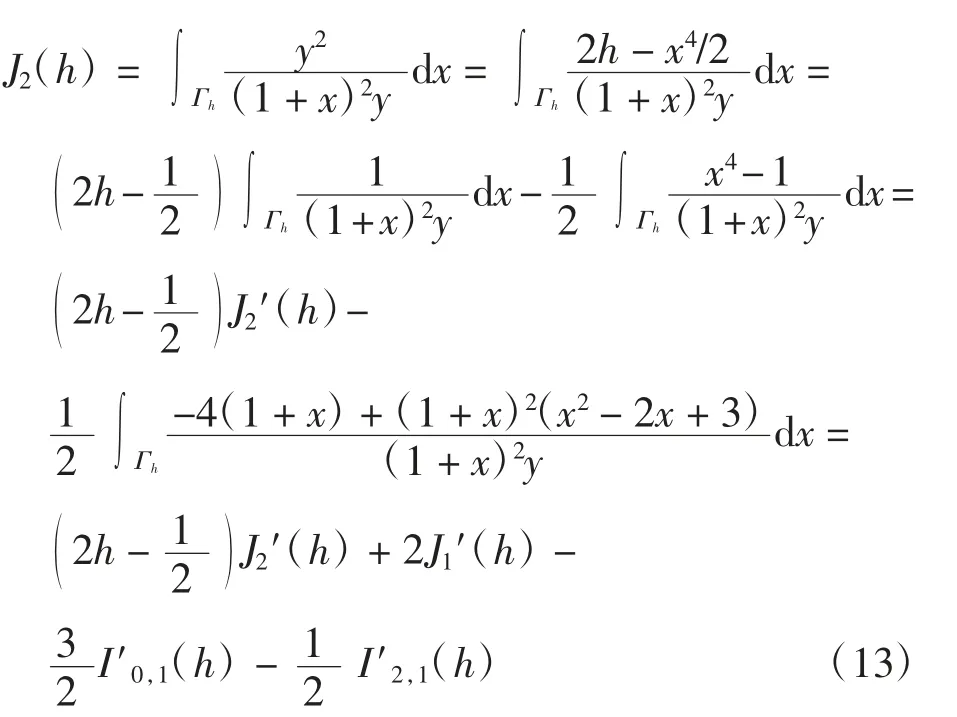
利用式(6)和式(12)可得
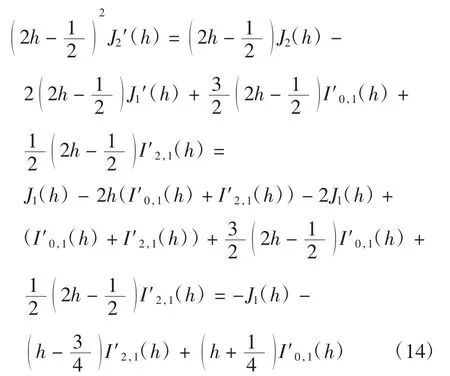
在式(8)中令α1=x-2,利用式(6)和式(14)可得
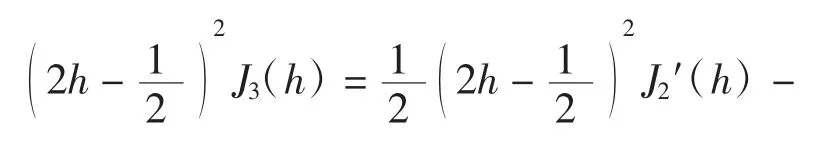
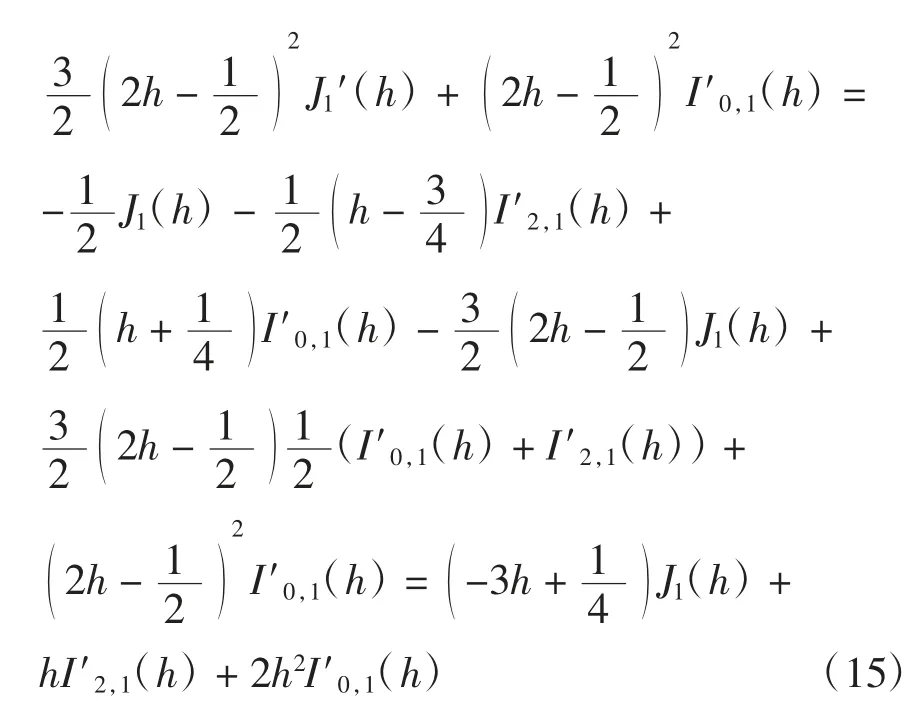
将式(12)和式(15)代入式(9)可得
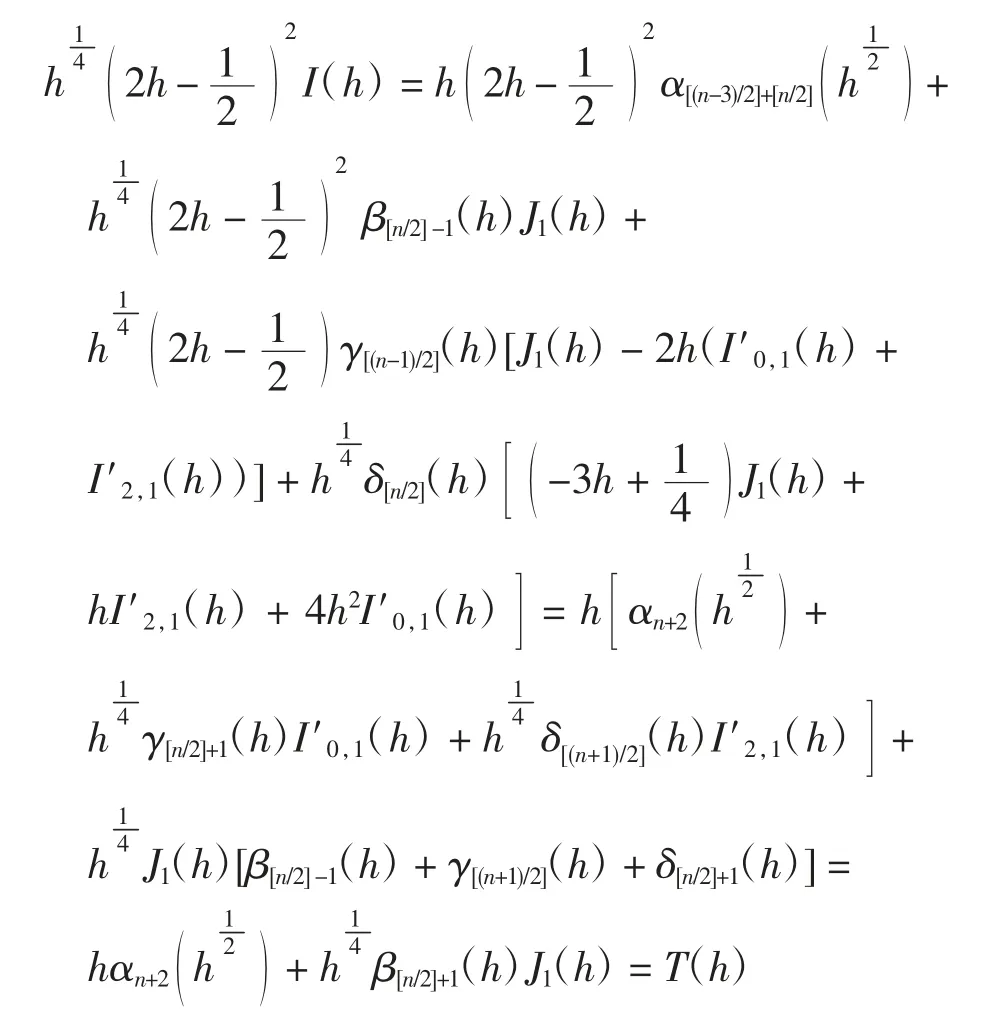
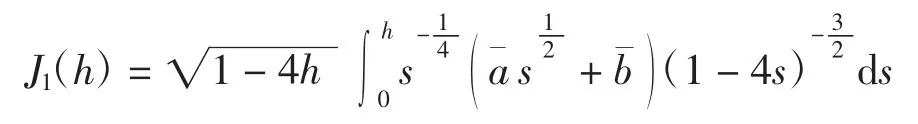

将函数T*(v)从开区间(0,1)解析延拓到复区域

定义G=GR,r⊂D,D为一单连通区域,∂G=C=CR,r为简单闭曲线,
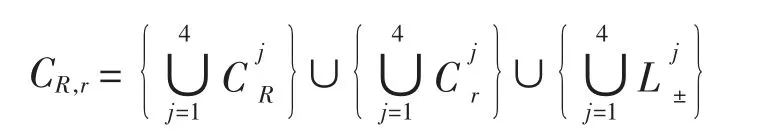
其中:CRj={v∈D,|v|=R≫1}且v属于第j象限,j=1、2、3、4;Cr1,3={v∈D,|v-(±1)|=r≪1},Cr2,4={v∈D,|v-(±i)|=r≪1},L±1,3={v∈R:1+r≤|v|≤R},L±2,4={v∈iR:1+r≤|iv|≤R}.根据文献[11]有如下引理9成立.
引理9解析函数T*(v)和(v)在复区域D⊂C上满足:
(2)当v∈L±j,j=1、2、3、4时,Im(T*(v))的零点个数不超过[n/2]+1.
由引理9的(1)可得,当r→0+时,T*(v)在的旋转数不超过10-1.
由引理9的(3)可得
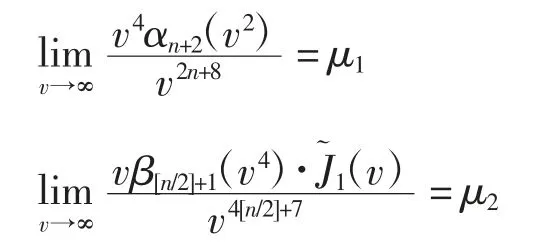
μ1、μ2为常数,因此有,故T*(v)在的旋转数不超过2n+8+10-1.
综上,T*(v)在G的边界C上的旋转数不超过2n+4[n/2]+16+,则T(*v)在G上的零点个数不超过2n+4[n/2]+16.显然,v=0是T*(v)的零点,结合T*(v)在开区间(-1,1)是关于v的奇函数,可知T*(v)在v∈(0,1)的零点个数不超过n+2[n/2]+7,即Z(n,2)≤n+2[n/2]+7.
情况3当k≥3时,对式(11)关于h求导得

对式(3)关于h求二阶导数得
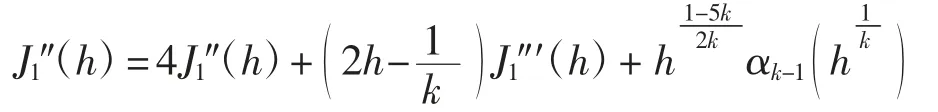
进而有
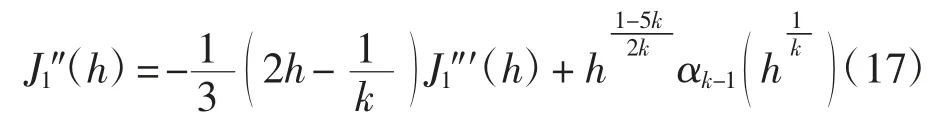
将式(17)代入式(16)可得
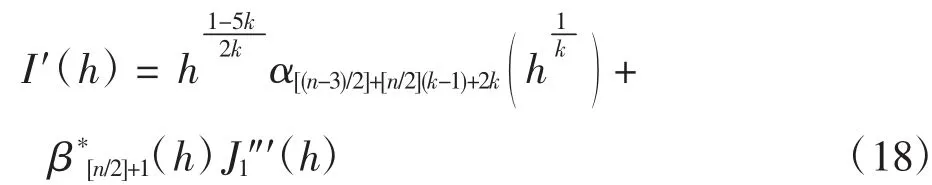
另一方面,将式(17)代入式(11)可得

利用式(18)和式(19)计算得
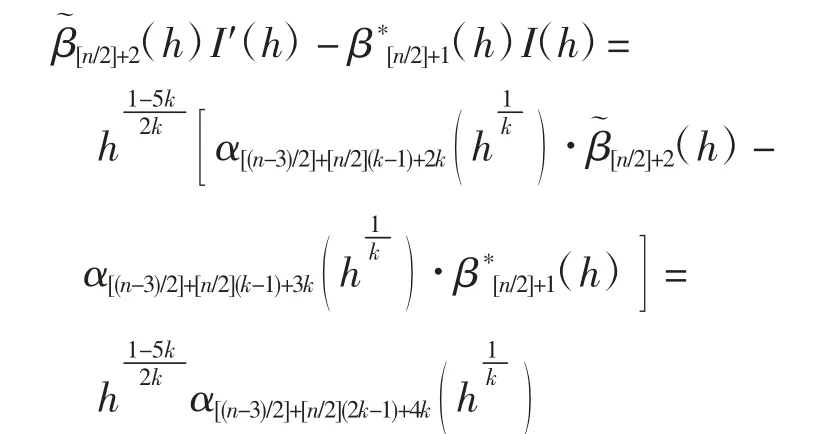
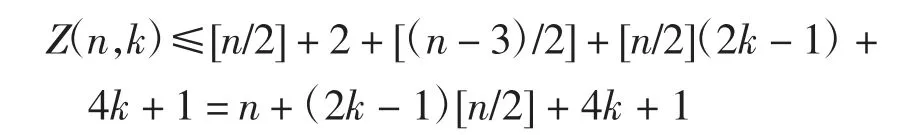
综上,定理证毕.
