内嵌运行优化与动力电池梯次利用的光储充换电站多阶段规划

葛少云，孙 睿，刘 洪，徐正阳，李维宇

（天津大学 智能电网教育部重点实验室，天津 300072）

0 引言

近年来，多个国家提出了碳中和的气候目标，并将其上升为国家战略［1］。电动汽车的进一步普及是实现碳中和目标的有效途径之一［2］。对于电动公交车而言，其动力电池（EVB）的更换模式能够实现能量的快速补给；而通过有序的充电管理，换电模式还可以消除充电负荷峰谷差，降低用能成本，提高资产利用效率。因此，换电站（BSS）成为电动公交车补充电能的一种新型高效模式。在该模式下，如何安排动力电池的购置、使用、淘汰，即如何在长时间尺度上规划充换电站，是决定其投资运营效益的关键。而随着电动汽车市场规模的扩大，如何有效处理退役动力电池也逐渐成为业界的关注焦点。将其重组为储能（ES）成为电池梯次利用的有效途径之一。

国内外已有较多关于充换电站的研究，但大多侧重于充换电站的运行调度［3-4］、选址优化［5］与充换电路径规划［6］，仅有少数研究分析了充换电站的容量配置规划问题。文献［7］建立了基于蒙特卡罗模拟的动力电池梯次利用容量计算模型，提出了一种考虑动力电池梯次利用的光伏换电站容量优化配置方法，但是简化了充换电站的运行过程，忽略了运行优化对容量配置的影响。文献［8］分析了分时电价机制下电动汽车换电站的运行特性，以换电站年综合成本最小为目标，建立了换电站电池容量优化模型。文献［9］提出了考虑电池组配送的换电站容量规划模型，分析了不同配送次数下采取直接充电、错峰充电、电池入网充电3 种充电方式时集中充电站的容量配置方案。文献［8-9］在计算经济效益时给出了动力电池的运行年限，然而在更长的时间周期上，换电需求的增加会影响动力电池的使用寿命，使其运行年限无法确定，此时文献［8-9］的方法不再适用。由于可以减少超前投资以及容量冗余产生的多余维护费用，多阶段规划已经在区域综合能源规划［10］、变电站规划［11］、储能输电网联合规划［12］等多个领域得到了广泛的应用。公交线路的建设是一个长期的过程，公交线路的增加会带来换电需求的阶跃性变化。因此，提出一种考虑运行优化的充换电站多阶段规划模型十分必要。

另一方面，目前关于动力电池梯次利用的研究主要分为动力电池梯次利用的关键技术研究［13］、动力电池梯次利用的应用场景研究［14］这2 个方面。在大部分的应用场景中，运营主体从外界购入梯次利用电池，将其作为储能使用，并对梯次电池设置充放电约束。但是在充换电站的应用背景下，关于动力电池从正常使用到梯次利用的全寿命周期应用的研究鲜见报道。文献［7］针对光伏充换电站，采用蒙特卡罗模拟法得到动力电池在规划年限内每年梯次利用的容量比例，但存在以下问题：动力电池采用随机使用的方法，每年需要梯次利用的电池数量不确定，且没有对其进行优化，可能会增加投资运行成本；对于梯次利用的储能，没有考虑充放电次数以及放电深度对其使用寿命的影响，而是直接设置淘汰率，建模比较简单，与实际情况有所出入。因此，在充换电站背景下给出一种考虑预备退役的动力电池梯次利用方案，有计划地安排动力电池正常使用、预备退役、梯次利用和淘汰，具有重要的应用价值。

针对上述问题，本文基于充换电站的全寿命周期，提出了一种内嵌多时间尺度运行优化且考虑动力电池梯次利用的光储充换电站多阶段规划模型。首先，基于不同的时间尺度，构建包含多阶段容量配置、阶段内使用、日内运行的3 层框架，揭示三者间的相互影响关系；其次，分别针对容量配置、日内运行构建优化数学模型，在规划阶段内考虑动力电池与储能的使用寿命，有计划和有针对性地使用动力电池与储能单元，给出动力电池在充换电站应用背景下正常使用、预备退役、梯次利用与淘汰的全过程使用方案；然后，基于光储充换电站内规划与运行的相互作用关系，提出一种嵌套优化的求解方法；最后，通过算例验证所提模型和方法的合理性与有效性。

1 充换电站的多阶段规划框架

1.1 充换电站的构成

本文所研究的电动公交车光储充换电站主要由光伏电池阵列、动力电池组、储能系统和充放储换电系统组成，具体结构如图1 所示。图中，Z为充换电站内的储能单元数量。

图1 光储充换电站的结构Fig.1 Structure of charging and battery swapping station with photovoltaic and energy storage

1）光伏电池阵列。

光伏电池阵列将太阳能转换成电能，为充换电站供电。目前，光伏发电基本可以实现平价上网，相较于从配电网购电，自建光伏用于供电的经济性更好。因此，在不扩建场地的情况下，本文在建设初期购入足够的光伏电池板，并一次性建设完成，后续不再增加光伏容量。

2）动力电池组。

动力电池组由多块动力电池组成，主要为电动公交车的行驶提供电能支撑。从全寿命周期角度而言，当因充放电达到一定的循环次数而使容量保持率［7］下降到淘汰临界点时，动力电池会被重组为储能单元进行梯次利用。同时，还需通过购入一定数量的动力电池来保障电动公交车的使用需求。

3）储能系统。

储能系统作为充换电站的灵活性资源，通过其储存和释放电能可实现消纳光伏、降低运行成本、参与配电网削峰填谷等功能。储能系统由Z个储能单元构成，储能单元由外部购买或由动力电池淘汰重组得来，可以单独充放电。储能单元的使用寿命耗尽后被淘汰。

4）充放储换电系统。

充放储换电系统用于实现动力电池的充电、储能单元的充电与放电、光伏接入、充换电站与配电网的功率交换以及电动公交车动力电池的更换。

1.2 基于建设时序的充换电站3层规划框架

电动公交车的换电需求会随着公交线路的建设进程分段阶跃性增长，因此需将光储充换电站的规划分为多个阶段。本文考虑多阶段规划涉及的不同时间尺度，对充换电站的规划进行分层优化，具体如下。

1）第1层：多阶段容量配置。

第1 层用于在整体规划初期对充换电站各阶段的动力电池数量与储能单元容量进行优化，以充换电站的全寿命周期成本最小化为目标函数，以各阶段新增设备与淘汰设备的容量为决策变量，确定变量结果后将其作为已知条件传递至下一层。

2）第2层：阶段内设备使用方案确定。

第2 层用于在各阶段初期确定该阶段动力电池和储能单元的使用方案，将该阶段决定消耗的循环寿命合理地分配到每一天，以提高规划运行的经济性。将该层得到的使用方案作为日内运行的约束条件传递至下一层，将所得阶段末的设备剩余寿命传递至该层的下一阶段，并将所得设备的残值传递至上一层。

3）第3层：日内运行优化。

第3 层用于对充换电站的日内运行调度进行优化。目标函数为日运行成本最小化，决策变量为日内各时段动力电池的充电功率、储能单元的充电和放电功率，运行约束条件为第1 层、第2 层的已知条件。通过计算日内运行成本得到年运行成本，然后将其传递至第1层。

在充换电站的规划过程中，多阶段容量配置会影响阶段内设备使用方案确定及日内运行优化，而阶段内设备使用方案、日内运行优化又会分别通过设备残值和年运行成本对多阶段容量配置产生影响。为此，本文提出充换电站的3层规划框架，如图2所示。首先，生成N个阶段充换电站内设备的容量配置结果；其次，根据容量配置结果生成各阶段内设备的使用方案；然后，对各阶段内的Sce种场景进行日内运行优化；最后，计算年运行成本、全寿命周期成本，更新所有阶段充换电站内设备的容量配置结果，并重复上述优化和计算过程，直到获得最优的规划结果。

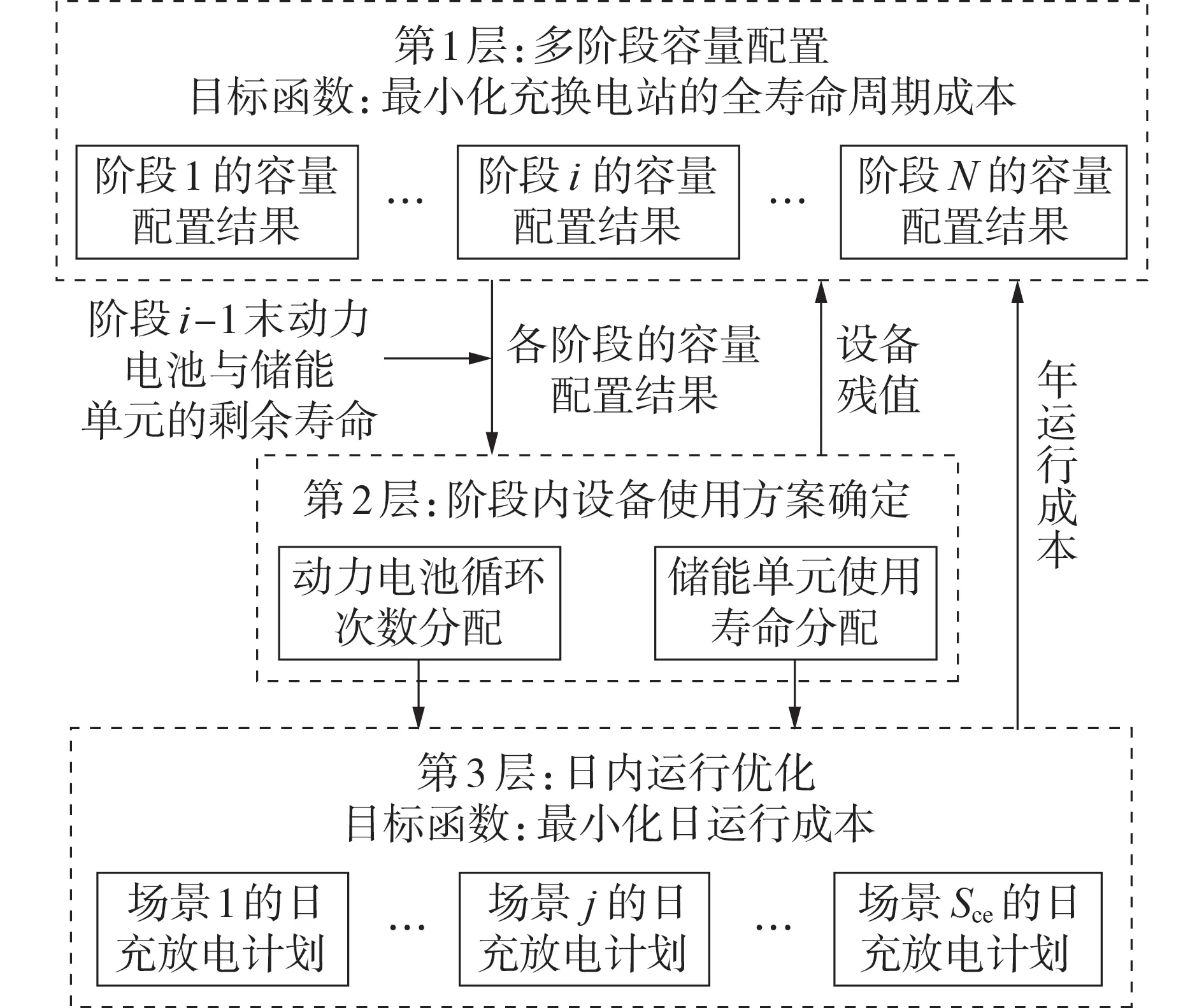
图2 充换电站的3层规划框架Fig.2 Three-layer planning framework of charging and battery swapping station

2 多阶段容量配置模型

多阶段容量配置模型的目标函数为最小化全寿命周期成本，具体包括规划周期内的设备投资成本、运行维护成本和设备残值，如式（1）所示。

式中：FRV，j为第j台设备的残值；CVal，j为第j台设备的价值；Nalr，j为第j台设备已经消耗的寿命；Nall，j为第j台设备可以使用的寿命。

多阶段容量配置的决策变量为各阶段新增、淘汰的动力电池数量和储能单元容量，分别用矩阵Enew、Eretired表示：

3 阶段内设备使用方案确定

3.1 动力电池的使用方案

本文将某阶段计划淘汰的动力电池称为预备退役电池，其他动力电池称为非预备退役电池。预备退役电池的选取优先考虑容量保持率低的动力电池，即按照剩余循环次数从少到多的顺序进行选取。在阶段内应将预备退役电池的剩余循环次数尽可能用完。本文将2 种动力电池分别排成队列，从队列首端取电池进行使用，使用后换下充电，充满电后将其加入队列的尾部，由此实现2 种电池在所有阶段内各自均衡使用。

预备退役电池与非预备退役电池矩阵Eφb，i可表示为：

式中：l=0，1，…，X2，i-1；x=1，2，…，sreq；Di，x(l)为阶段i依次退役l种且剩余X2，i-l种预备退役电池时，在换电需求场景x中安排预备退役电池运行的天数。

3.2 储能单元的使用方案

本文采用雨流计数法［15］计算得到储能单元的循环次数nc以及对应的放电深度，将放电深度记为DDOD(1)、DDOD(2)、…、DDOD(nc)，然后根据储能单元的放电深度与循环寿命之间的关系曲线计算储能单元的剩余寿命R，如式（19）所示。

4 日内运行优化模型

在充换电站的运行中，将动力电池按照其状态分为满电电池、正在充电电池、待充电电池、正在使用电池。预备退役电池和非预备退役电池分别运行。动力电池的状态转换关系式如式（23）所示，状态转换示意图如图3所示。

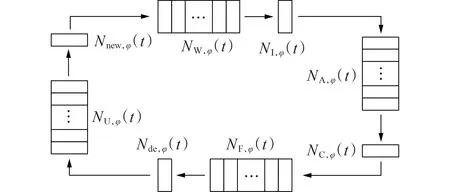
图3 动力电池的状态转换示意图Fig.3 Schematic diagram of state transition of electric vehicle batteries

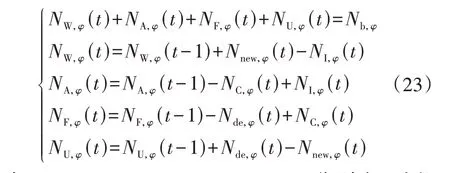
式中：NW，φ(t)、NA，φ(t)、NF，φ(t)、NU，φ(t)分别为t时段待充电电池、正在充电电池、换电后剩余的满电电池、正在使用电池的数量；Nb，φ为充换电站内预备退役或非预备退役电池的总数量；Nnew，φ(t)为t时段新卸下的电池数量；NI，φ(t)为t时段新投入充电的电池的数量；Nde，φ(t)为t时段新投入使用的电池数量；NC，φ(t)为t时段新充满电的电池数量。

日内运行优化的目标函数为最小化日运行成本，如式（24）所示。

约束条件包括功率平衡约束、与配电网的功率交换约束、储能单元约束、动力电池使用约束、换电需求约束、调度连续性约束等，具体见附录A。

5 模型求解方法

本文采用规划运行嵌套优化的方法求解多阶段规划模型。若没有具体的设备容量配置结果和阶段内设备使用方案，则日内运行优化不能得到运行条件，无法进行求解。因此，规划层的优化方法应在优化过程中生成一系列待选方案。只有启发式优化算法可以满足这一要求，故本文选择遗传算法进行优化求解。然而多阶段规划问题的优化维度很高，经典的遗传算法存在收敛速度慢、产生大量不可行解、容易陷入局部最优等缺点，为此本文选用一种变种群规模的遗传算法，通过扩大和减小种群规模，减少重复计算，扩大搜索空间；并在生成遗传个体时，考虑边界条件，将明显的不可行解筛除，避免计算其适应度值，从而减少无用计算。

日内运行优化模型为线性整数规划问题，采用YALMIP 平台的CPLEX 求解器进行求解。根据各种场景下求得的日运行成本计算充换电站的年运行成本。将年运行成本代入规划层的目标函数中，迭代求解全寿命周期成本的最小值。

多阶段规划模型的具体求解步骤如下。

步骤1：生成数量为Npop的初代种群、个体代表Enew和Eretired，确定适应度函数、选择率、杂交率、变异率，设定最大迭代次数Ngen。

步骤2：根据种群的容量配置结果，确定各阶段内的设备使用方案和梯次利用计划。

步骤3：利用CPLEX 求解器求解种群个体在各种典型场景下充换电站的日运行成本，继而计算各阶段的年运行成本。

步骤4：计算所有个体的全寿命周期成本，然后计算适应度值，进行选择、交叉、变异，生成下一代种群。

步骤5：将父代与子代个体组合成集合，将集合内适应度值最大的个体作为最优个体，将最优个体作为参考，计算每一代集合中所有个体与最优个体之间差值的绝对值并求和，将其记作diff。

步骤6：将前Ngen/4 代的种群个体数量均设为Npop，然后对每一代的diff进行比较。若第g代种群的diff小于第g-1 代种群的diff，则按式（25）所示比率ρ减少种群数量；若第g代种群的diff大于第g-1 代种群的diff，则按式（26）所示比率σ增加种群数量；若第g代种群的diff等于第g-1 代种群的diff，则保持种群规模不变。同时设置种群规模的最大、最小边界。

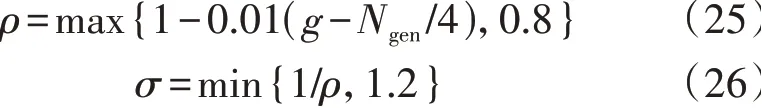
步骤7：重复步骤2—6 直到达到最大迭代次数，其中具有最优适应度值的个体即为最优解。

6 算例分析

6.1 算例概况

本文以中国北方某电动公交车充换电站为例进行规划仿真。当地公交公司在未来8 年中每2 年增设1 条公交线路。根据电动公交车换电需求的增长情况，将充换电站的规划周期划分为4 个阶段（阶段1—4），各阶段的持续时间均为2 a。公交新增线路在各阶段的运营信息见附录B 表B1，充换电站的运行相关参数见附录B表B2。

光伏出力情况参考文献［16］。待规划区采用分时电价，峰时段（12:00—16:00、19:00—22:00）、平时段（09:00—12:00、16:00—19:00、22:00—24:00）、谷时段（00:00—09:00）的充电电价分别为1.20、0.80、0.34 元／（kW·h），峰时段、平时段、谷时段的放电电价分别为0.96、0.80、0.30 元／（kW·h）［17］。将1 d 以10 min为间隔分为144个时段。

为了说明本文所提多阶段规划方法的有效性和经济性，设置以下规划方案进行对比分析。

方案1：采用本文所提内嵌多时间尺度运行优化的多阶段规划方法，考虑动力电池预备退役与梯次利用。

方案2：在整个规划周期初购置动力电池和储能单元的单阶段规划。

方案3：各阶段购入相同数量的动力电池，并进行多阶段规划，不预先决定需要淘汰的动力电池，考虑动力电池的梯次利用。

方案4：采用内嵌运行优化的多阶段规划方法，动力电池均衡使用，不考虑动力电池预备退役，对耗尽循环次数的动力电池进行梯次利用。

6.2 方案1的多阶段规划结果分析

规划层采用变种群规模的遗传算法对优化配置模型进行求解，设种群数量为200，最大迭代次数为40 次，变异率为0.01，杂交率为0.7，选择率为0.5，选取全寿命周期成本为适应度函数。计算总时长约12 h。求解得到各阶段动力电池数量与储能容量的配置结果，如表1所示。

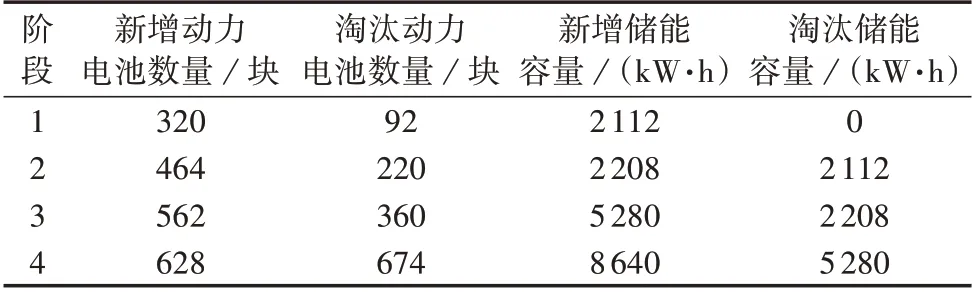
表1 多阶段的容量配置结果Table 1 Multi-stage capacity configuration results

阶段3夏季充换电站的运行结果见图4。由图可知：00:00—09:00为用电低谷时段，充换电站从电网购电，为动力电池和储能充电；09:00—12:00为电价平时段，光伏为充换电站供电，且为了满足换电需求，为部分动力电池充电，并将剩余电能出售给电网；12:00—16:00为用电高峰时段，也是光伏出力的峰时段，此时光伏与储能的电能主要出售给电网，同时满足部分动力电池的充电需求；在16:00—19:00时段，光伏向少量储能、动力电池提供电能，且向电网出售的电能减少直至为0；19:00—22:00为另一个用电高峰时段，储能为必要的动力电池充电，并向电网出售部分电能；22:00—24:00时段内换电站停止工作。

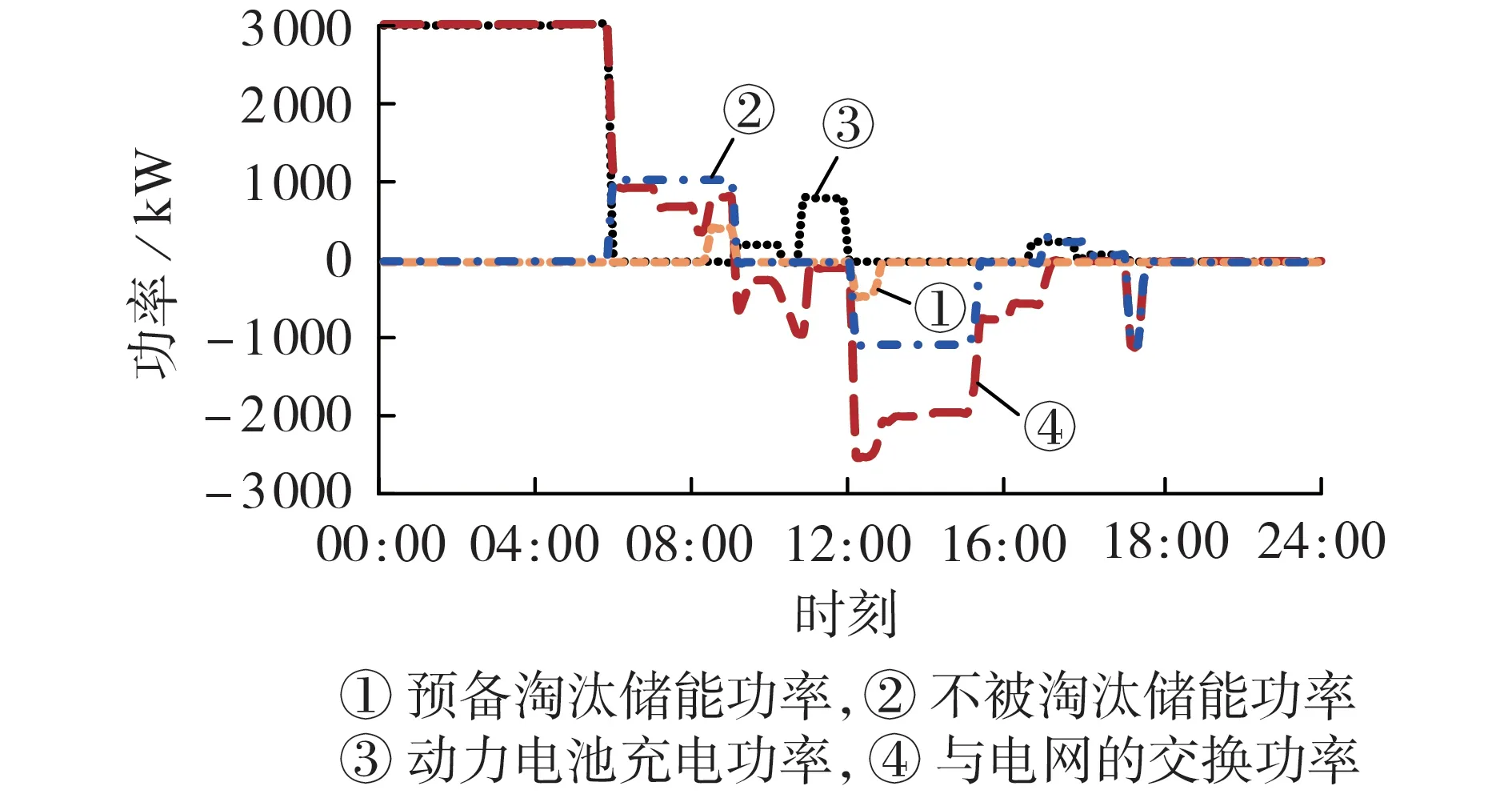
图4 阶段3夏季某场景下充换电站的运行结果Fig.4 Operation results of charging and battery swapping station under a summer scenario in third stage

综上所述，动力电池主要在电价谷时段和光伏出力较大的时段充电，会尽量避免在电价峰时段充电；储能在电价谷时段充电，在电价峰时段放电，且优先为动力电池充电，剩余电能向电网出售。这种运行策略使得充换电站尽可能减少从电网购电的成本，从而降低运行成本。

6.3 经济性对比

4种方案在各阶段的规划结果和成本见表2。1）多阶段规划经济性对比。

表2 不同方案的规划结果与成本Table 2 Planning results and costs of different schemes

方案2 在规划初期决定所有需要购置的动力电池和储能单元，不对动力电池进行梯次利用，在其循环寿命结束后，作为退役电池低价处理。相较于方案2，方案1 的设备投资成本大幅减少，且不用维持较大的设备规模，减少了设备冗余，降低了维护成本，但是代价是运行成本增加了519.87万元，但与减少的投资成本和维护成本相比，增加的成本偏小。可见，多阶段规划可以明显降低充换电站的全寿命周期成本，方案1比方案2降低了22.20%。

方案3在各阶段投入相同数量的动力电池，且各阶段的新增储能由淘汰的动力电池组成。相较于方案3，方案1 在前期减少了容量剩余，降低了投资成本、维护成本，全寿命周期成本减少了235.96 万元，降低了5.35%。可见，内嵌运行优化的方法在降低投资成本和运行成本方面是有效的。

2）动力电池预备退役使用方案效果分析。

为了验证动力电池预备退役使用方案的有效性，对比分析方案1 与方案4。在方案4 下：不预先决定需要淘汰的动力电池，所有动力电池均衡使用，且在同一阶段的使用次数相同；动力电池循环寿命耗尽后，在阶段末进行淘汰重组并梯次利用，因此同一阶段购入的动力电池同时被淘汰；按照方案1 购买各阶段的动力电池和阶段1 的储能单元。方案1和方案4下各阶段的年运行成本如图5所示。

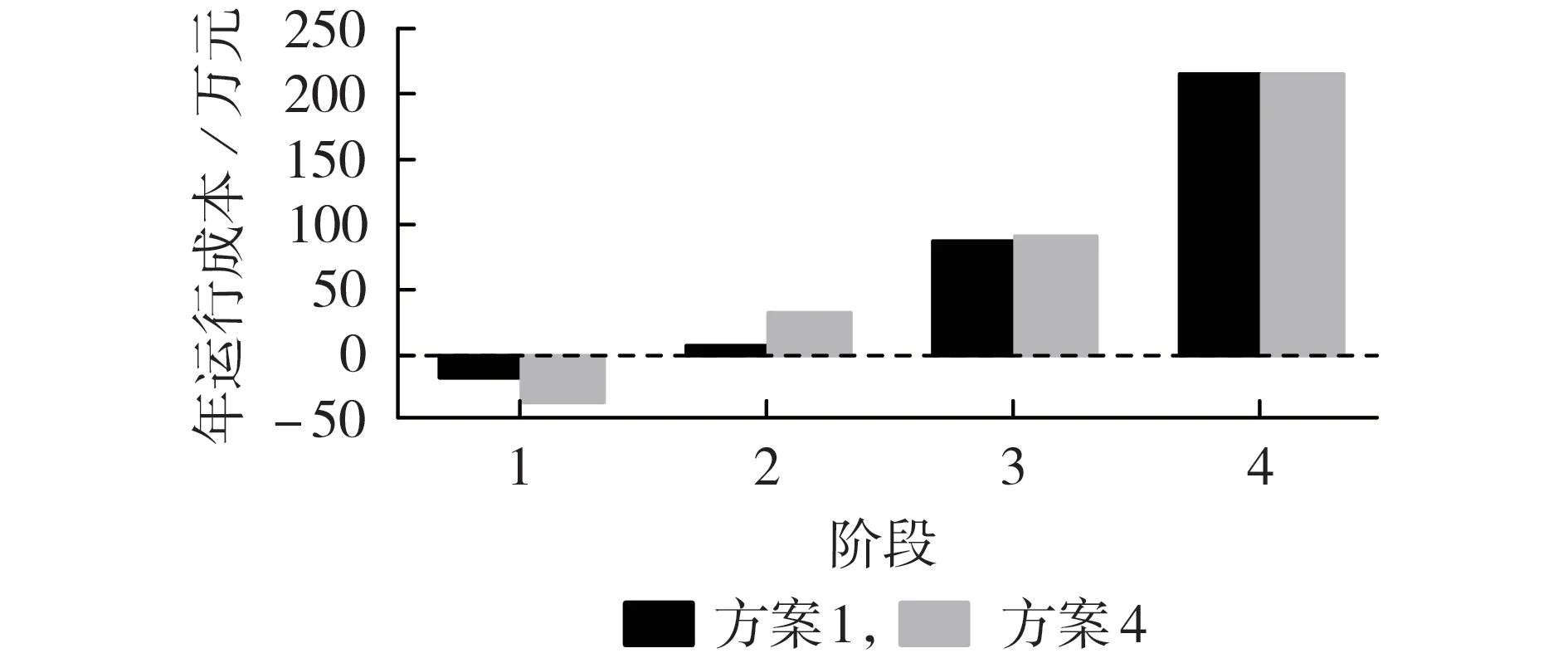
图5 方案1和方案4下各阶段的年运行成本Fig.5 Annual operation costs of each stage in Scheme 1 and Scheme 4

由图5 可知：在阶段1，光伏和储能出力较为充足，方案2和方案4均获得了部分售电收益，但方案1获得的收益较少，这是因为方案1 设置了预备退役电池的循环使用次数，使其充电计划受限，而方案4没有该限制；在阶段2，方案1按计划新增储能，方案4因动力电池寿命没有耗尽而不能新增储能，所以方案1 的运行成本更小；在阶段3，相较于方案4，方案1 的动力电池数量较多，储能容量较小，故其运行成本较小；在阶段4，方案1 与方案4 的运行成本持平。相较于方案4，方案1在各阶段淘汰的动力电池数量可控，不会出现个别阶段没有梯次利用的电池作为储能的特殊情况。从整个规划周期来看，相较于方案4，方案1的总运行成本减少了11.86万元，节省了2 688 kW·h 的储能容量，设备残值增加了98.04 万元，提高了11.23%，故方案1 的全寿命周期成本比方案4 降低了2.52%左右。上述结果验证了动力电池预备退役方案的有效性。

7 结论

本文构建了一种多阶段、阶段内与日内的规划运行3 层模型，采用嵌套优化的求解方法，提出了一种考虑动力电池梯次利用的电动公交车充换电站的多阶段规划方法，通过理论与算例仿真分析得到的主要结论如下。

1）在充换电站的规划中，相较于单阶段规划，多阶段规划方法能够降低22.20%左右的全寿命周期成本；相较于将购入的动力电池平分到各阶段的传统规划方法，本文所提内嵌运行优化的多阶段规划方法可以在前期减少超前投资和容量冗余产生的维护成本以及时间成本，使全寿命周期成本减少235.96 万元，降低了5.35%，显著提高了充换电站的运营经济性。

2）相较于不受控制的动力电池均衡使用方法，本文预先决定需要淘汰的动力电池，有计划地使用电池并进行梯次利用，在各阶段配置的储能单元容量更加合理，可以减少11.86 万元的运行成本，节省2 688 kW·h 的储能容量，提高11.23%的设备残值，从而减少2.52%左右的全寿命周期成本。

未来将在本文所提规划模型的基础上，继续研究光伏出力、换电需求不确定性对充换电站运行与规划的影响，进而增强多阶段规划方法的鲁棒性。

附录见本刊网络版（http：//www.epae.cn）。