考虑新增电动汽车充放电中断风险的聚合商调频辅助服务投标策略

2022-10-15李永刚孙浩潮周一辰武健伟

电力自动化设备 2022年10期

李永刚，孙浩潮，周一辰，武健伟，李沙，覃露

（华北电力大学电力工程系，河北保定 071003）

0 引言

调频辅助服务是为了保证频率处于正常范围而由电网、用户等相关方提供的一项调频服务［1］。我国的调频辅助服务发展迅速，部分地区的能源监管局先后发布了调频辅助服务市场建设方案。我国首个实际结算的区域调频辅助服务市场，为南方监管局从2020年12月开始试运行的调频辅助服务市场，并于2021年4月结算试运行。

第三方独立主体是调频辅助服务市场中的重要组成部分。其中，随着电动汽车（EV）的大规模推广与应用，EV 储能资源已经成为参与调频辅助服务的重要主体。但是，由于单辆EV 具有容量小、充电行为随机、独立参与电力系统调节存在困难等缺点［2］，其一般由聚合商进行聚合后参与市场投标并获得收益。聚合商通过给予补贴来吸引空闲EV 用户参与系统调节，并基于调频辅助服务市场中标价格与给予补贴价格之间的差价实现获利。EV 的入网时刻等参数具有随机性，加之用户主观行为的影响，使得EV 的充放电行为具有较大的不确定性。构建该不确定性模型及制定决策策略的优劣，已成为影响聚合商所获投标收益的关键因素。

针对构建EV 不确定行为模型的问题：文献［3］提出了基于韦伯-费希纳定律的可入网EV 用户响应模型，利用偏差阈值制定合理的补贴电价，使得净收益最大化；文献［4］建立了参与日前与实时阶段的EV、温控设备模型，验证了不同类型的负荷共同参与辅助服务的可行性；文献［5］针对高校网络EV 供电设备的应用，提出了一种可有效降低平均单位能耗的预测调度框架；文献［6］对比了非协调和协调EV 充电方式，明确了这2 种充电方式对电网的影响，并采用蒙特卡罗法处理其不确定性；文献［7］考虑EV的不确定性，对EV参与调频进行仿真，提出了EV 参与调频面临的挑战；文献［8］首先基于电池等参数对EV进行分类，然后控制中心以最小化总负荷方差为目标，根据EV 集群情况及相关负荷信息，对可调度负荷进行优化。针对聚合商的决策问题：文献［9］首先对柔性负荷进行聚类，然后构建了用电满意度函数，在不同的补贴价格基础上，以聚合商收益最大化为目标构建聚合商决策模型；文献［10］提出了随机动态混合整数线性规划算法，用于求解EV集群的最优协调竞价问题；文献［11］基于储能设备等，针对日前市场制定了最优竞价策略，并分析了电池数量及价格对竞价策略的影响；文献［12］针对电网供需不一的问题，制定了需求响应工作机制，根据需求响应综合目标对聚合商进行决策优化。

目前已有的研究主要侧重于EV 充放电随机性建模及聚合商决策模型的优化求解，较少考虑EV用户主观中断充放电引发聚合商参与调频辅助服务存在违约风险的情况。实际上，由于聚合商控制度与用户满意度之间存在矛盾关系，同时不同级别控制度的EV参与调频辅助服务的能力差别很大，故聚合商应对EV控制度进行全面评估和精细划分，以期有效降低调频违约风险。

针对新增EV用户参与调频辅助服务，存在部分用户主观中断充放电的行为，从而使得聚合商净收益降低的问题，本文提出了一种考虑EV主观中断充放电风险的聚合商调频辅助服务投标策略。首先，在聚合商与交易中心互动流程的基础上，提出多级别EV 充放电控制度的分析方法，采用Stevens 定律确定辅助服务补贴电价与用户响应率之间的关系，并基于蒙特卡罗法建立不同级别控制度EV 充放电响应容量的评估模型。然后，考虑EV 中断退出风险，以最大化聚合商净收益为目标，基于条件风险价值CVaR（Conditional Value at Risk）建立计及中断退出风险的聚合商投标决策模型，并采用MATLAB中的YALMIP、CPLEX 工具箱实现优化求解。最后，以日前24 h 调频辅助服务市场中某EV 聚合商对目标资源投标为算例，验证所提投标决策模型的有效性。

本文创新之处在于：①以控制度为基础建立EV充放电模型，可反映聚合商对EV 的控制程度；②引入EV 用户满意度、EV 用户厌恶度及中断退出风险等，能够准确描述用户对聚合商控制EV 的接受程度；③提出计及CVaR 的聚合商投标决策方法，可计及EV 用户主观中断充放电行为给聚合商带来的风险损失。

1 EV参与日前调频辅助服务市场分析

1.1 EV聚合商参与调频辅助服务流程

第三方独立主体可参与调频辅助服务市场的投标，并提供相应的服务，以获得收益。EV 聚合商参与日前调频辅助服务市场的流程图如图1 所示，具体步骤如下。

图1 EV聚合商参与日前调频辅助服务市场的流程图Fig.1 Flowchart of EV aggregators participating in day-ahead frequency regulation auxiliary service market

步骤1：在日前，交易中心在调频辅助服务市场中发布信息，其中包括参与调频辅助服务的名单、次日24 h各时段的调频容量需求值［13］、市场出清价格、调频性能要求等。

步骤2：聚合商统筹整合EV 调频资源，利用蒙特卡罗法统计各时段EV的充放电容量，制定参与调频辅助服务市场投标的最优决策。

步骤3：交易中心确定聚合商的中标相关信息，组织日前出清；聚合商对EV 充放电进行日前安排，提供中标容量所要求的调频辅助服务需求，并对充、放电补贴进行日前出清。

1.2 EV控制度

对于新增EV用户参与调频辅助服务，根据聚合商对EV 充放电的控制程度，可将EV 划分为充放电完全控制、充放电不完全控制、仅充电控制3 类。本文引入EV 控制度，并按照控制度由高至低的顺序，将上述3 类EV 分别定义为1—3 级控制度EV，具体区别如表1 所示。以充电为例，1—3 级控制度EV的具体区别见附录A图A1。

表1 不同控制度EV的区别Table 1 Difference among EVs with different control degrees

1）1级控制度EV。

1 级控制度EV 的控制度最高，其离网时刻由聚合商根据需要决定，用户不得干涉。当EV 处于1 级控制度时，聚合商以满足EV 基本荷电状态SOC（State Of Charge）需求值后的第二次充放电完成时间及等待时长作为决定EV是否离网的主要因素，即当处于1 级控制度的EV 满足基本SOC 需求值且完成第二次充放电，或等待时长超过最大值时，聚合商才安排其离网。此外，聚合商也可自主安排EV的起始充电时间及其他行为。

当EV参与调频辅助服务时，其基本SOC需求值根据行驶里程和电池过充限制确定，取二者中较小者，如式（1）所示。

式中：Sj，f为EVj的基本SOC 需求值；Sj，mile为满足EVj用户行驶里程的SOC需求值；Sj，max为防止EVj电池过充的SOC 阈值；Sj，in为EVj的初始SOC 值；Ssoc为聚合商设定的防电池过充的SOC最大值，Lj，mile为EVj用户的行驶里程；Lj，max为EVj用户的最大行驶里程，其值由EVj的性能决定；P100为EV 行驶100 km 的耗电量；Ej，N为EVj的电池容量。EVj达到基本SOC 需求值的充电时长Tj，realch可表示为：

式中：Pch为EV的充电功率；κch为EV的充电效率。

在1 级控制度EV 中，聚合商考虑EVj的SOC 需求及等待时长（当EV 需求与市场需求相违背，EV 暂停与电网相连，直至两者需求再次一致时所需要的时长），统筹安排EVj的离网时刻tj，endch1。tj，endch1的计算式及相关等式约束条件为：

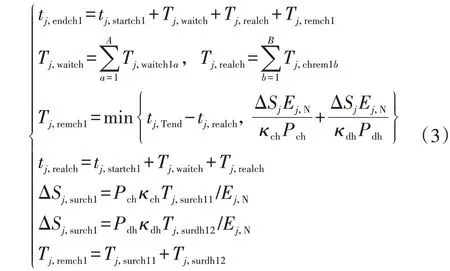
式中：tj，startch1为EVj的入网时刻；Tj，waitch为EVj的总等待时长；Tj，remch1为EVj的入网剩余时长；Tj，waitch1a为EVj参与充电时的第a次等待时长；A为聚合商安排的等待次数；Tj，chrem1b为EVj参与充电时的第b次充电时长；B为聚合商安排的充电次数；tj，Tend为EVj所在时段的截止充电时刻；tj，realch为EVj达到基本充电需求的时刻；ΔSj为EVj在第二次充放电时SOC 的最大变化值；ΔSj，surch1为EVj达到基本SOC 需求值后进行充放电的SOC变化值；Tj，surch11、Tj，surdh12分别为EVj达到基本SOC 需求值后的充电、放电时长；Pdh为EV 的放电功率；κdh为EV的放电效率。不等式约束条件为：

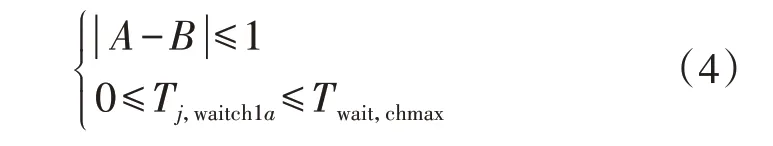
式中：Twait，chmax为EV 的最大等待时长，其值由聚合商确定，且在第二次充放电过程中不对放电容量进行统计。其中，第一个不等式是为了保证等待过程与充电过程交替安排，直至EV退出电网。

当EVj放电时，其可放电SOC 值ΔSj，dh1及达到聚合商设置的SOC 最低值Smin时的放电时长Tj，realdh1的计算式为：

式中：Sj为EVj参与放电时的初始SOC值。

对于1 级控制度EV 而言，其放电模型与充电模型类似，主要不同点在于：①与式（1）和式（2）不同，式（5）计算的是可放电SOC 值ΔSj，dh1及达到SOC 最低值时的放电时长；②与充电过程相反，EV 放电达到SOC最低值后，若要再次进行充放电，则先进行充电再进行放电。

2）2级控制度EV。

2级控制度EV 的控制度比1级控制度EV 稍低。此类EV的离网时刻由用户根据主观需求决定，但必须保证在无等待时长的情况下满足EV 的正常充电需求，否则，此类EV 用户主观不选择离网；同时，聚合商可对其进行充放电安排。2 级控制度EV 的离网时刻及其SOC值是决定EV是否离网的主要因素，即：一旦到达离网时刻，EV 必须立刻离网；或当EV的SOC 达到基本需求值时，即使EV 未到离网时刻，聚合商也会安排其离网。

当2 级控制度EVj的离网时刻tj，endch2确定时，必须满足式（6）所示条件，以确保2 级控制度EV 的充电时长较长（与3级控制度EV相比）。

式中：tj，startch2为2级控制度EVj的入网时刻。

对于2 级控制度EV 而言，其离网时刻选取为用户自行设定的离网时刻tj，endch21与满足基本SOC 需求值而确定的离网时刻tj，endch22二者中的较小值，如式（7）所示。

式中：Tj，waitch2c为EVj参与充电时的第c次等待时长；Tj，chrem2e为EVj参与充电时的第e次充电时长；C、E分别为聚合商安排的等待次数、充电次数。

同样地，2 级控制度EVj的可放电SOC 值ΔSj，dh2及其达到出行基本SOC 需求值时的放电时长Tj，realdh2的计算式为：

2 级控制度EV 的放电模型与充电模型类似，主要不同点在于：与式（7）相比，式（8）表示的是可放电SOC值ΔSj，dh2及可达到的放电时长Tj，realdh2。

3）3级控制度EV。

3 级控制度EV 的控制度低于2 级控制度EV。虽然此类EV 的离网时刻与2 级控制度EV 类似，均由用户决定，但若此类EV在不满足基本充电需求时就离网，则会导致聚合商无法安排放电计划。且由于此类EV 的控制度不高，无法对其进行调控，故本文只对部分时刻（由目标市场需求决定）的此类EV进行补贴。3 级控制度EV 的充电模型较简单，其离网时刻需满足：

式中：tj，endch3为3 级控制度EVj的离网时刻；tj，startch3为3级控制度EVj的入网时刻。

1.3 EV充放电补贴电价设置及容量评估

由于通过充放电参与调频辅助服务不是EV 用户的基本需求，聚合商需制定合适的补贴电价以吸引用户参与该额外辅助服务。本文根据Stevens 定律确定新增EV 用户响应率与聚合商补贴电价之间的关系，根据目标市场需求确定各时段的补贴电价。

1）基于Stevens 定律的补贴电价响应率模型及响应容量求解。

聚合商组织新增EV 资源参与日前调频辅助服务市场的投标，用户根据参与控制度级别与参与时长获得合理的补贴费用。为了吸引新增EV 用户参与调频辅助服务，本文基于Stevens 定律设计聚合商的补贴电价机制。

为了更好地反映新增EV 用户参与调频辅助服务的响应率，采用Stevens 定律［14］建立补贴电价与用户响应率之间的关系模型。Stevens 定律认为：感觉量的大小与刺激量的乘方成正比，即心理量是物理量的幂函数。Stevens定律的一般表达式为：

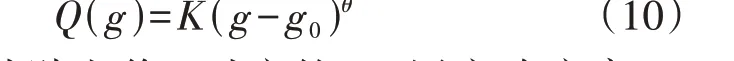
式中：Q(g)为补贴电价g对应的EV 用户响应率；K为用户响应常数；θ＞1为指数；g0为初始补贴电价。

考虑到EV控制度的差异性，可基于式（10）构建不同控制度等级EV用户的响应率模型，如式（11）所示。不同控制度等级EV 用户响应率与补贴电价之间的关系曲线见附录A图A2。

式中：Qi(g)为补贴电价g对应的i级控制度EV 用户的响应率；Qmax为EV 用户的最大响应率；Ki为i级控制度EV 用户的响应常数；gi0、gi1分别为i级控制度EV 用户的初始补贴电价、最高补贴电价。值得注意的是：当求取EV 用户的充电响应率时，共有3 个等级的控制度，即i=1，2，3；当求取EV 用户的放电响应率时，共有2 个等级的控制度，即i=1，2。在后文中，若无特殊说明，则控制度等级i遵照上述原则取值。

2）基于蒙特卡罗法的EV充放电容量评估方法。

在通常情况下，EV 的不确定性主要是由入网及离网时刻参数的不确定性以及用户行为的主观性导致的，因此需对其不确定性进行建模，基于此求解EV 能提供的调频辅助服务总容量，求解过程见附录A图A3，具体步骤如下。

（1）根据聚合商对EV的控制度差异采取分类安排：对于1 级控制度EV 而言，聚合商安排其充放电计划，包括充电时长、入网时刻、离网时刻等，且为了保护EV 电池，在安排充电计划时，先安排充电再安排放电；对于2 级控制度EV 而言，聚合商安排其充放电计划，但不安排其离网时刻；对于3 级控制度EV 而言，聚合商只安排其充电计划，对离网时刻和放电计划均不进行安排。

（2）计算各控制度等级EV 的充电容量。对于1级控制度EV用户而言，首先确定其所处目标市场是否正处于充电需求状态，若是，则直接进行充电；否则，进行第一次等待，之后再进行第一次充电。在此后的充电过程中，若目标市场出现放电需求，则进行等待，当再次出现充电需求时，再次进行充电，直到完成充电需求任务。然后，求取这一充电时段内的第二次充放电时间，合理分配充电、放电时间，使得此次充放电的SOC 值保持一致。当达到放电时刻时，聚合商将其转变为正常用户，不计入其放电容量，直至再次达到充电时间将其转变为新增用户，重新计入充电容量。同时按照式（3）计算1 级控制度EV 的离网时刻及其充电容量。对于2 级控制度EV用户而言，其充放电过程与1 级控制度EV 用户类似，由聚合商安排其充放电，不同之处在于不再安排其进行第二次充放电及其离网时刻；根据用户设定的离网时刻及满足基本SOC 需求值的时刻，按照式（7）计算其实际离网时刻和充电容量。对于3 级控制度用户而言，聚合商不对其充电计划进行调整，只对相应的充电时段进行补贴，不调整其充电时长，且不安排第二次充放电。同时只对入网时刻和离网时刻都在充电时段内的用户进行实际充电时长和充电容量计算。

（3）与计算各控制度EV 的充电容量类似，计算各控制度EV的放电容量。

2 基于CVaR的聚合商决策模型

2.1 EV用户满意度和中断退出风险评估模型

虽然新增EV 用户在参与调频辅助服务之前已默认与聚合商达成充放电契约，但由于新增EV用户的主观行为可能会对EV充放电进行干扰，为了提高聚合商的净收益，在制定投标决策时应计及对用户主观违约因素的考量。因此，本节分别建立了EV用户满意度、EV 用户厌恶度及EV 中断退出风险评估模型。

在定性划分EV控制度等级的基础上，进一步考虑用户对各控制度等级EV的接受程度、聚合商装置的可靠性等因素，提出EV 用户满意度ξ的定量计算方法。ξ能够直接反映EV 用户对聚合商控制的满意程度。在第k个调查问卷中，i级控制度EVj用户满意度ξk，ij的计算式为：

式中：αk，ij，user为在第k个调查问卷中，i级控制度EVj用户对自身设备被控的接受程度；μi，re为聚合商的i级控制度EV控制装置（如充电桩、通信设备等）的可靠性系数。考虑到EV用户满意度与EV用户厌恶度概率互补，第k个调查问卷中i级控制度EVj用户的厌恶度ζk，ij，dis可表示为：

EV 用户厌恶度将产生不遵循合约、强行终止充放电行为的可能性，第k个调查问卷中i级控制度EVj用户的中断退出风险指标ζk，ij，risk可表示为：

式中：ck，ij，pun为第k个调查问卷中i级控制度EVj用户愿接受惩罚的系数。

当EV 用户的中断退出风险指标值大于突变值mi，midd（即ζk，ij，risk＞mi，midd）时，用户存在离网的风险。第k次调查问卷中i级控制度EV中断充放电概率pk，i的计算式为：

式中：nk，i、Nk，i分别为第k个调查问卷中中断充放电、参与充放电的i级控制度EV编号；nk，i，total、Nk，i，total分别为第k个调查问卷中中断充放电、参与充放电的i级控制度EV 总数量；Pnk，i，ch(dh)、PNk，i，ch(dh)为第k个调查问卷中i级控制度EV的充（放）电功率。

2.2 基于CVaR的风险损失度量

CVaR是在某一置信水平下，风险损失大于风险价值VaR（Value at Risk）的风险损失期望值［15］。则对于给定的置信水平β，VaR、CVaR值可表示为［16］：

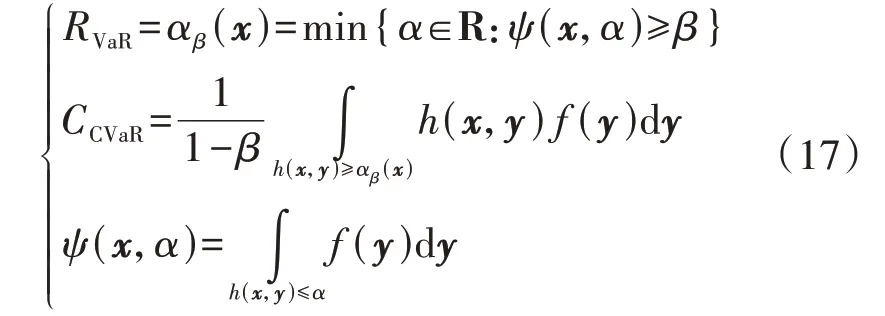
式中：RVaR、CCVaR分别为VaR、CVaR 值；x∈X为n维决策优化变量，X⊂Rn为目标解可行集；y∈Rm为m维随机向量；f(y)为y的概率密度函数；h(x，y)为损失函数；ψ(x，α)为风险损失不大于边界值α的分布函数。

在式（17）中，αβ(x)难以求解，故采用式（18）所示辅助函数Fβ(x，α)计算CVaR值［16］。

在本文中，厌恶度高的EV用户可能出现未到约定时刻离网等违约情况，给系统运行带来风险。因此，采用CVaR 能有效衡量EV 充放电中断给聚合商带来的风险损失。

假设新增EV 用户的充放电中断概率服从正态分布，当出现中断退出风险时，聚合商所产生的充电风险损失Gch、放电风险损失Gdh可表示为：

2.3 聚合商投标决策模型

本节在满足交易中心发布的日前调频辅助服务市场性能要求的基础上，以聚合商净收益最大为目标，建立考虑CVaR的聚合商投标决策模型。

2.3.1 目标函数。

聚合商的日前调频补偿收益主要为充放电容量收益［17］，成本主要包括EV 响应成本、风险损失，则最大化聚合商净收益的目标函数可表示为：

式中：f(t)为时段t的聚合商净收益；ftotal(t)为时段t聚合商参与日前调频辅助服务市场投标所获总收益；fcost(t)为时段tEV 参与日前调频辅助服务市场投标的响应成本，包括充电响应成本fc(t)和放电响应成本fd(t)；Fch(dh)CVaR(t)为时段tEV 的充（放）电风险损失；δ≥0为风险厌恶系数，通过调整风险厌恶系数的取值以反映不同的市场环境，表现聚合商对风险的关注程度；cca为EV参与日前调频辅助服务市场充放电的容量补贴单价；y(t)为时段t聚合商参与日前调频辅助服务市场的投标容量。

采用上述基于Stevens 定律的用户响应率模型，根据用户响应率求得聚合商的补贴电价，然后根据式（11）和式（12）可求得时段t的EV 充电响应成本fc(t)和放电响应成本fd(t)分别为：

2.3.2 约束条件

聚合商投标决策模型的约束条件主要包括EV容量约束、持续充放电时间约束及投标容量约束。

1）EV 容量约束。结合式（12），EV 可响应容量应满足自身容量限制，即：

式中：Y(t)为时段t日前调频辅助服务市场的需求量。

2.3.3 求解过程

本文求解的变量为聚合商净收益、各级控制度EV 的出力容量。首先确定决定变量——各级控制度EV的出力容量，然后采用MATLAB调用YALMIP、CPLEX 工具箱求解聚合商投标决策模型，具体求解步骤如下：

1）初始化目标市场的调频容量需求量及其技术特点、EV 行驶里程、入网时刻、离网时刻等相关数据；

2）采用蒙特卡罗法求取EV 的充电、放电总容量，同时建立EV充电、放电补贴电价体系；

3）根据时段t目标市场的需求量及EV 的充电、放电容量等相关信息，在确定决策变量的前提下，利用MATLAB 调用YALMIP、CPLEX 工具箱，制定时段t日前辅助服务市场的投标策略；

4）求解时段t聚合商净收益的最大值后，返回步骤3），直至全部时段的投标策略求解完成。

3 算例仿真及结果分析

3.1 Stevens定律及其优势分析

当某市的补贴电价为50 元／（MW·h）时，新增EV 用户开始参与调频辅助服务；当补贴电价为300元／（MW·h）时，新增EV 用户全部参与调频辅助服务；当补贴电价为226.78 元／（MW·h）时，有50%的新增EV 用户参与调频辅助服务。将相关数据代入Stevens 定律，可得用户响应率随补贴电价的变化曲线如图2所示。

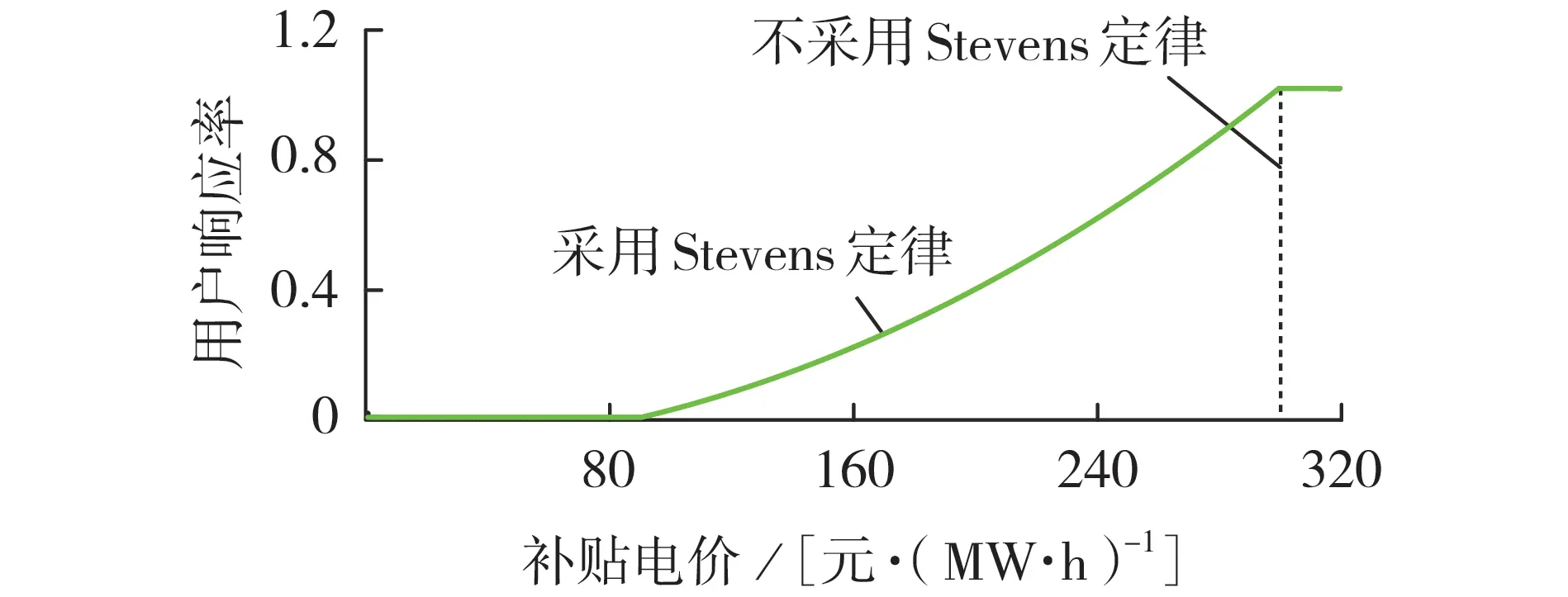
图2 用户响应率随补贴电价的变化曲线Fig.2 Curve of user response rate vs. subsidy electricity price

由图2可知：当采用Stevens定律时，用户响应率会随着补贴电价的增大而增大，直至达到最大值，聚合商可以精准定位响应率；当不采用Stevens 定律时，聚合商无法确定响应量，只能采取全部响应的方式，即用户响应率为1；不采用Stevens 定律时确定的补贴电价不小于采用Stevens 定律时确定的补贴电价，表明在大多数的情形下聚合商采用Stevens 定律可以有效降低补贴成本。

3.2 计及CVaR的投标决策模型的参数设置

3.2.1 日前调频辅助服务市场参数设置

在某市的日前调频辅助服务市场中，交易中心根据调度中心的需求发布目标资源调频容量需求量，如附录A 图A4 所示（规定需求量为正值时聚合商充当负荷，需求量为负值时聚合商充当电源）。交易中心的容量补贴电价为430元／MW。

3.2.2 EV可充电容量及可放电容量仿真分析

设定EV 入网时刻服从正态分布N（8.75，0.6），2 级控制度EV的离网时刻服从正态分布N（14，0.8），3 级控制度EV 的离网时刻服从正态分布N（9.5，5.56）；EV充电初始SOC服从正态分布N（0.4，0.1）［18］，EV 放电初始SOC 服从正态分布N（0.95，0.1）；EV 电池容量为30 kW·h，充放电功率为6.6 kW，充放电效率为0.9［19］。某聚合商共能聚合30 000 辆EV，其中1—3 级控制度EV 的数量比例为6∶3∶1。蒙特卡罗法模拟次数为20次。

若聚合商不对EV充电进行调控，则基于蒙特卡罗法可以得到无序充电策略下2 级控制度EV 的充电容量如图3 所示。若聚合商对EV 充放电进行调控，则基于蒙特卡罗法可以得到不同控制度EV的可充电、放电容量如图4所示。

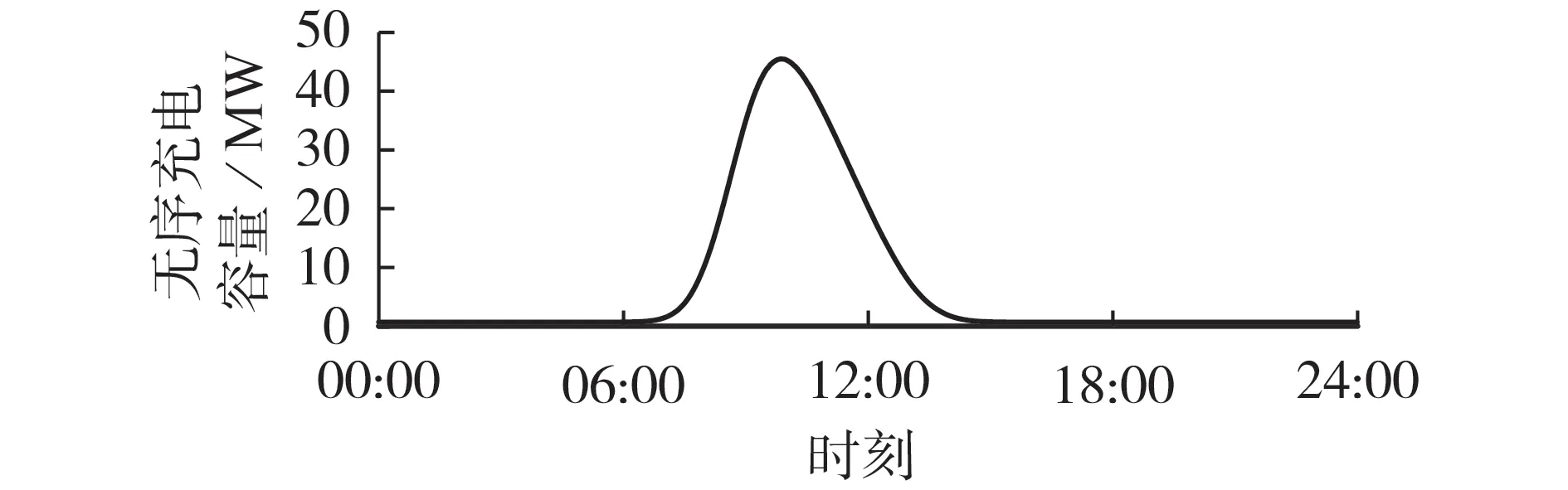
图3 无序充电策略下2级控制度EV的充电容量Fig.3 Charging capacity of EVs with secondary control degree under disordered charging strategy

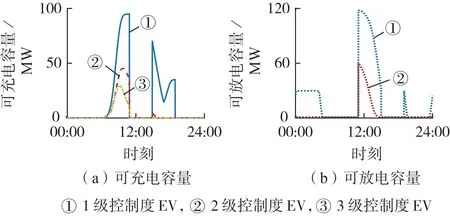
图4 不同控制度EV的可充电、放电容量Fig.4 Available charging and discharging capacities of EVs with different control degrees

由图3 与附录A 图A4 可知，无序充电策略不能满足目标市场的调频容量需求，验证了聚合商进行调控的必要性。对比图3与图4可直观看出，在聚合商的调控作用下，EV 在充电时间及充电容量等方面与无序充电策略存在较大的区别。由附录A 图A4和图4 可知，聚合商成功对1、2 级控制度EV 进行聚类并对充放电时间进行转移，聚合商设置的充放电时段与目标市场调频容量需求时段相同。上述结果验证了聚合商调控EV的有效性。

3.2.3 EV资源的参数设置及基本处理

不同控制度EV的参数具体包括两方面：①包含持续充放电时间、中断充放电概率、中断惩罚价格［20］等，如表2 所示（首先以调查问卷形式获得基础数据，然后设置聚合商设备的可靠度为99%，根据式（13）—（16）获得EV中断充放电概率）；②包含1.3节中以1 h 为时段间隔的各时段可充电、放电容量，见附录A图A5。

表2 不同控制度EV的参数Table 2 Parameters of EVs with different control degrees

3.3 计及CVaR的投标决策模型的结果分析

3.3.1 聚合商净收益分析

设置置信水平β=0.95，风险厌恶系数为0.4，将其代入投标决策模型中，求解可得聚合商的净收益如图5 所示。由图可知，聚合商净收益在00:00—04:00、08:00—19:00 时段相对较高。00:00—04:00时段是EV经历第二次充电后的放电高峰时段，故可响应放电容量较大，08:00—15:00是EV 的主要充放电时间段，故可响应容量较大，而聚合商在前一阶段的部分充电容量被迁移到15:00—19:00，故在该时段的可响应容量也较高。

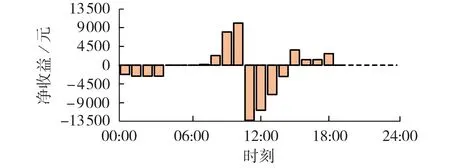
图5 聚合商净收益Fig.5 Net income of aggregators

可响应容量与聚合商净收益息息相关。故为了达到聚合商净收益最大化的目标，聚合商应尽可能在目标市场调频容量需求时段聚合较多的充放电容量。由于1、2 级控制度EV 允许安排充放电行为，聚合商可按照合适的时段安排其充放电行为。此外，针对3 级控制度EV 的充电行为，应采取引导措施，使其尽可能多地在目标市场调频容量需求时段内充电。

在求取聚合商的最大净收益时，风险厌恶系数取0.4，一般不会出现因风险厌恶系数过大导致聚合商不参与投标的现象。图5 中部分时段的净收益极低，这主要是因为该时段内聚合商的可响应容量过小。

3.3.2 风险厌恶系数对各级控制度EV 出力及净收益的影响

以时段9（08:00—09:00）的投标决策策略为例，风险厌恶系数分别取值为0.1、0.4、0.8、1.2、1.6、2.0时，不同控制度EV 的出力和聚合商净收益如图6 所示。由图可知：不同控制度EV的出力和聚合商净收益均随着风险厌恶系数的增大而减小，说明随着风险厌恶系数增大，聚合商为了规避风险，将选择更加保守的投标策略；当风险厌恶系数从0.1逐渐增大到2.0时，2、3级控制度EV的出力占总容量的比例逐渐减小，但1 级控制度EV 的出力比例逐渐增大，说明当风险厌恶系数逐渐增大时，聚合商更倾向于中断风险程度低、惩罚价格低的1级控制度EV出力。

图6 不同控制度EV的出力、聚合商净收益与风险厌恶系数的关系Fig.6 Relationship of output of EVs with different control degrees and aggregator net income vs. risk aversion coefficient

3.3.3 不同控制度EV 数量比例对聚合商净收益的影响

设置不同的1—3控制度EV的数量比例如附录A 表A1 所示。采用蒙特卡罗法进行仿真，可得不同数量比例下聚合商净收益如图7 所示。由图可以看出，随着1级控制度EV和2级控制度EV的数量占比增大，聚合商净收益增大，这主要是因为：相较于3级控制度EV，聚合商对1、2 级控制度EV 的控制度更强，可根据需要对其进行充放电安排；1、2 级控制度EV 的中断退出风险明显比3 级控制度EV 低，导致1、2 级控制度EV 的风险损失值低于3 级控制度EV。故聚合商应尽量引导新增EV 成为1、2 级控制度资源。由EV 数量比例为3∶6∶1、6∶3∶1、8∶1∶1 时的聚合商净收益结果可知，虽然1、2 级控制度EV 总数量占比相同，但随着1 级控制度EV 数量比例的增大，聚合商净收益也增大，这不仅是因为相较于2 级控制度EV，1 级控制度EV 中断充放电的风险更低，更因为1 级控制度EV 允许聚合商进行第二次充放电，增加了EV的可充放电容量。

图7 不同EV数量比例下的聚合商净收益Fig.7 Net income of aggregators with different EV number proportions

综上所述，聚合商净收益与不同控制度EV的数量比例密切相关，为了达到最大化聚合商净收益的目标，聚合商应采取相应的引导措施，例如：通过设置不同的补贴电价，以激励用户选择成为1 级控制度资源。

3.3.4 中断充放电概率的影响

当聚合商的设备可靠度为90%时，通过调查问卷的形式得到基础数据，根据式（13）—（16）可得中断充放电概率如附录A 表A2 所示。在大多数情况下，表A2 中的中断充放电概率比表2 中的中断充放电概率大，故将表2、表A2 中的概率分别称为低级别、高级别中断充放电概率。

同样以时段9（08:00—09:00）为例，当不考虑用户满意度时，聚合商默认用户满意度最高，不会出现用户中断退出的风险（即中断充放电概率为0）。设置风险厌恶系数为0.1、0.4、0.8，基于投标决策模型可得聚合商净收益如表3所示。

表3 不同中断充放电概率下的聚合商净收益Table 3 Net income of aggregators with different charging and discharging interruption probabilities

由表3 可以明显看出，相较于不考虑用户满意度的情况，考虑用户满意度时的聚合商净收益更低，这主要是因为考虑用户满意度时聚合商存在风险支出。虽然考虑用户满意度意味着存在CVaR 约束，聚合商的投资决策偏向于保守，净收益相对较小，但这更符合实际情况。相较于低级别中断充放电概率，当风险厌恶系数为0.1、0.4、0.8时，高级别中断充放电概率下聚合商净收益分别降低了5.37%、37.0%、79.5%，这充分说明当中断充放电概率较大时，为了最大化聚合商净收益，应采取措施以降低中断概率级别，否则聚合商只能采取更加保守的策略参与投标。