一种航空装备使用最优梯次间隔时间计算方法
2021-12-06田丰维肖楚琬刘松福
刘 嘉,田丰维,肖楚琬,刘松福
(1.海军航空大学,山东烟台 264001;2.辽宁工程技术大学,辽宁葫芦岛 125000)
航空装备在全寿命周期内要经过多次使用和翻修,合理地确定装备使用梯次间隔时间,是确保装备有序使用、避免出现修理积压的重要前提。所谓梯次间隔时间,是指在队同型各架飞机的剩余寿命的差值。机队飞机剩余寿命升序或降序排列时,机队剩余寿命将呈现阶梯状,如图1所示。因此,通常采用梯次控制指代机队飞机整体剩余寿命控制情况。机队剩余寿命梯次控制具有重要意义。例如,航空公司的运输机队通常有数十架飞机,它们在使用过程中需要进行各类检修,而修理厂的修理能力是有限的,如果不进行梯次控制,大量飞机同时达到大修期限,就会造成修理厂大修飞机积压。若机队可用飞机数量不足,将直接影响航空公司正常运营和效益。因此,合理控制梯次间隔时间,是避免飞机集中到寿送修的关键,如图1所示,4、5、6号飞机因同时接近大修时限寿,需要集中送修,从而影响了装备在位率。以往机队梯次控制大多是装备管理人员依据经验对飞机进行调配使用,使得管理预见性不足,极易出现盲目调配、远期近期统筹不佳、大中小修定期维护协调不畅等问题。

图1 梯次间隔时间及集中送修示意图Fig.1 Echelon interval time and the concurrent repairing
综上所述,必须使用一种方法对梯次间隔时间进行计算。以航空装备为例,目前使用的计算方法主要有梯次使用图形法和计算法。文献[1-2]概述了飞机梯次控制问题及其必要性;文献[3-4]介绍了改进的图形法,但这一方法主要基于当前机队寿命进行梯次计算,没有考虑大修能力,因此,仍可能出现大修积压问题;文献[5]介绍了发动机梯次管理的一种方法;文献[6-7]介绍了军用飞机梯次使用控制指标评价方法及基于训练数据的飞机梯次使用控制指标研究;文献[8-9]介绍综合考虑多种指标,尤其是飞行课目影响下梯次寿命计算方法;文献[10-12]介绍了基于多目标规划的飞机使用计划方法;文献[13-15]介绍了直升机梯次控制方法;文献[16-18]分别介绍了空空导弹梯次控制问题和锂离子电池使用梯次问题。以上研究可为本文提供较好参考依据,但对于如何解决实际剩余寿命下的梯次控制问题,仍须进一步研究。为此,本文提出一种综合考虑装备寿命、大修能力、日常使用等因素的装备使用梯次间隔时间计算方法,以解决上述问题。
1 关于梯次间隔时间的分析
梯次间隔时间Tg主要受修理厂修理能力和装备在位率约束影响。它和装备的翻修周期TF、装备修理耗时TR等因素直接相关。翻修周期TF指的是装备2次翻修间的使用时间,如某型飞机的翻修周期是2 000飞行小时,指的是每飞行2 000 小时,需用进厂大修1次。装备修理耗时TR,指的是每台装备的修理需用时间,此处使用的单位是等效飞行小时。假设对于某型飞机,每架飞机完成大修耗时180 天,根据历史统计,该型机在180 天内大约飞行1 000 小时,则该型飞机TR=1 000 等效飞行小时。下面分情形进行讨论分析。
1.1 情形1:TR在修理时间TRTR2种情况进行讨论。
1)Tg≤TR
当Tg≤TR时,装备使用及修理情况,如图2 所示。即1号机使用TF后,进厂大修,修理时间为TR(阴影部分),由于此时装备进厂梯次间隔时间为Tg,因此,1号机尚未出厂,2号机进厂,将出现2架飞机同时在厂大修情况(TR重叠区域即为同时在厂时间)。如果修理厂修理线数量无法同时满足2 架飞机修理需要,就会出现飞机积压。因此,根据修理厂修理能力,对Tg进行推算。

图2 Tg ≤TR 的送修情形Fig.2 Condition of Tg ≤TR
假设大修厂同时在修的飞机数量最多不超过n台,每次同时进厂飞机数量为nt,则应存在如下关系:
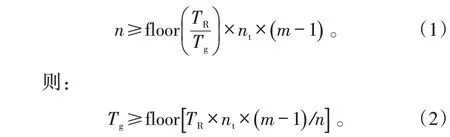
式(2)中:floor()∙是向下取整函数;m为最大翻修次数。
同时,积压的待修理飞机,也会影响部队的装备使用效率。假设部队共有飞机N架,规定的大修停飞率不大于p,则:
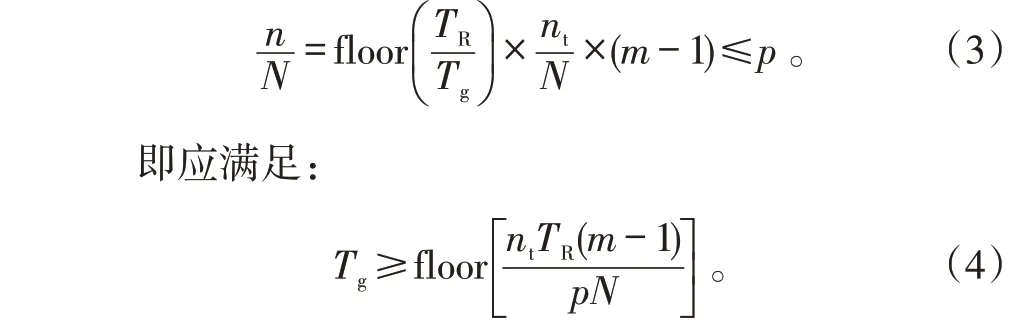
2)Tg>TR
当Tg>TR时,也可以形成梯次。这种情况如图3所示。其物理含义是前批飞机修理出厂后,后续飞机还没进厂,说明同时修理飞机数量就是单批次同时进厂飞机数量nt,因此,根据飞机在位率要求,有:

图3 Tg>TR 的送修情形Fig.3 Condition of Tg>TR

即:

这时,只要Tg≥TR,都可以形成梯次。
1.2 情形2:TR ≥TF
在修理时间TR≥TF时,区分Tg≤TR和Tg>TR2种情况进行讨论。
1)Tg≤TR
如图4 所示,前机没出厂,后机进厂,形成积压。同样,可根据修理能力对Tg进行推算,即修理能力限制下的梯次时间为:

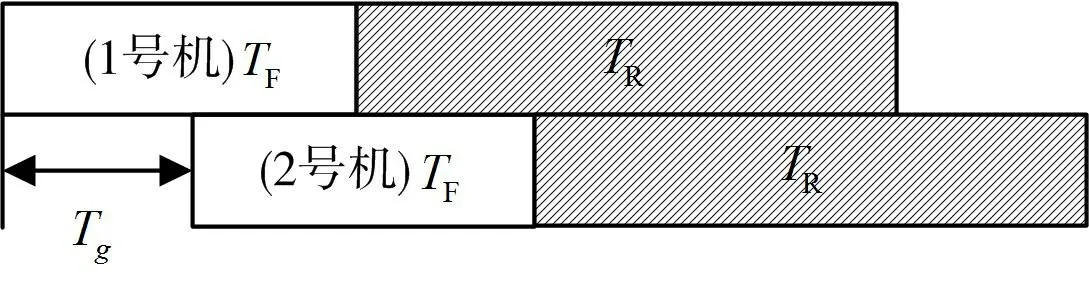
图4 Tg ≤TR 的送修情形Fig.4 Condition of Tg ≤TR
2)Tg>TR
当梯次间隔时间Tg>TR,也可以形成梯次,如图5所示。这种情况下,前批飞机修理出厂后,后续飞机还没进厂,同样,只要满足nt≤pN且Tg>TR就可以形成梯次。
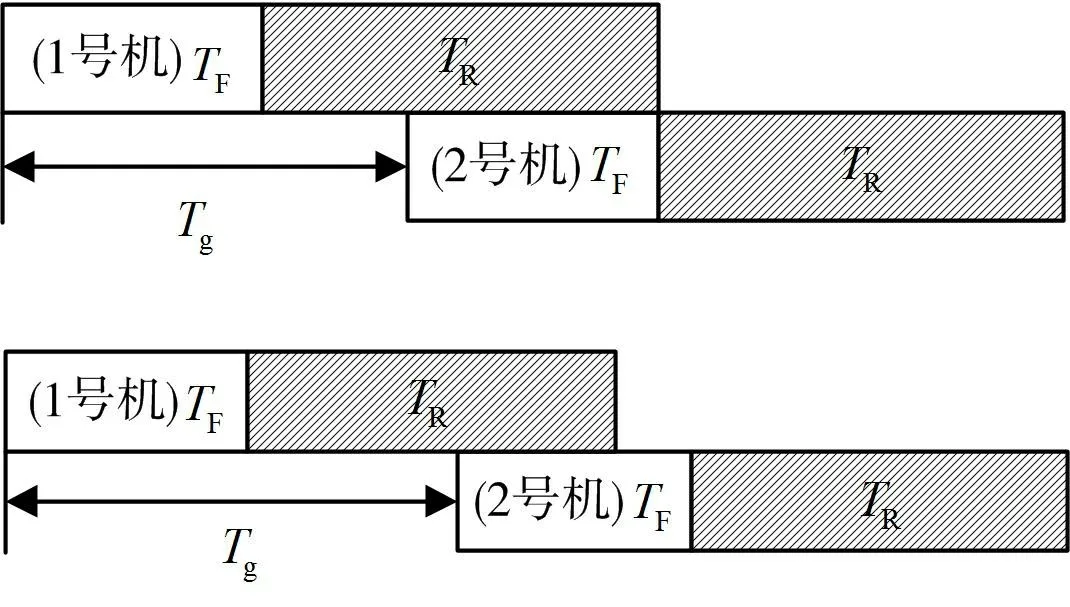
图5 Tg>TR 的送修情形Fig.5 Condition of Tg>TR
1.3 Tg 的上限分析
归纳1.1和1.2可以发现:

只要满足式(9),就可以形成梯次。但显然,Tg只能在一定范围内变化,如果Tg无限制增加,则无法使机队全部飞机形成梯次。因此,Tg还应满足以下关系:
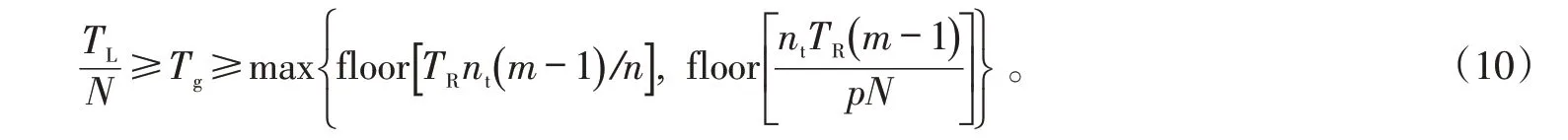
式(10)中,TL为装备全寿命时间。
1.4 梯次间隔时间数学模型小结
汇总以上各情形,如表1所示。
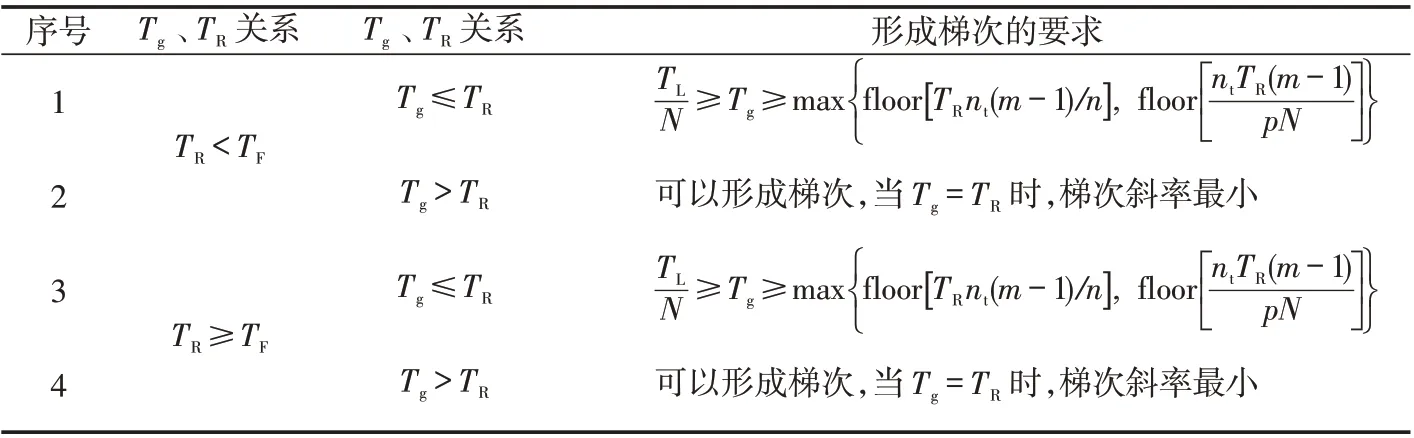
表1 梯次间隔时间模型归纳Tab.1 Summary of the echelon interval time model
2 最优梯次间隔时间算法
以上梯次间隔时间取值是1个区间范围。在实际使用中,装备使用者通常希望有1个最佳结果,以求使本单位装备尽快形成合理梯次。因此,本章主要针对实际装备寿命,建立最优梯次时间算法,进而为装备实际使用提供参考。具体算法,如图6所示。
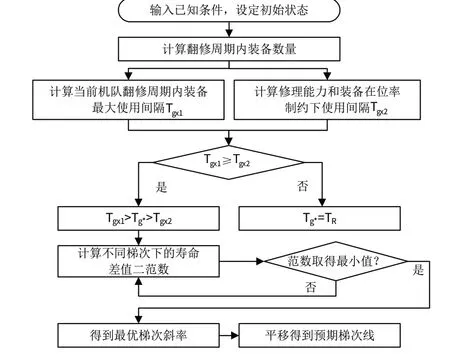
图6 最优梯次间隔时间算法流程图Fig.6 Flowchart of the optimal echelon interval time algorithm
算法过程如下。

步骤1:按式(11)计算当前机队翻修周期内装备最大使用间隔,式(11)中:TL.imax指当前机队内剩余寿命峰值;Nin-repair指翻修周期内装备数量。
步骤2:按下式计算修理能力和装备在位率制约下使用间隔,

步骤3:判断Tgx1和Tgx2关系,当Tgx1步骤4:当Tgx1≥Tgx2时,计算理想梯次间隔Tg.opt。方法如下:
a)令待计算的理想梯次间隔时间为x,则此时的梯次线可用下式表示,
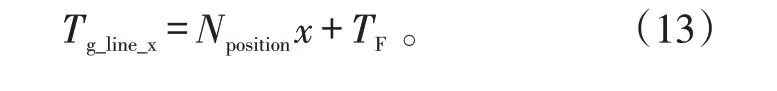
式(13)中:TF是装备翻修周期;Nposition是梯次线横坐标,对应了机队内飞机号码。具体如下:
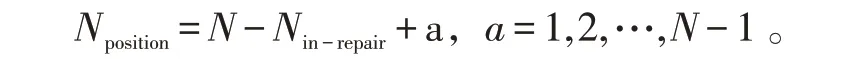
b)按下式计算装备余寿范数,
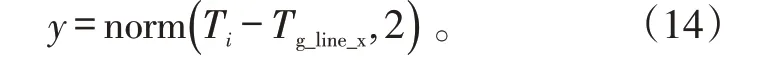
式(14)中:norm()∙为MATLAB 程序中的范数计算函数;Ti是Nposition对应的飞机当前剩余寿命;Tg_line_x是梯次线纵坐标。由于目的是使尽量多的装备尽快形成梯次,因此,采用了计算余寿平均二范数,并使用寻优求解的方法来计算梯次间隔。
c)判断y是否取得最小值,如果取得最小值,则此时的x即为待求最优梯次间隔时间,否则,继续更新x值,直到取得最小范数为止,则此时得到计算结果Tg.opt。
步骤5:根据计算结果,判断实际最优梯次间隔时间Tg*。具体判断方法如下:
a)当Tg.opt在[Tgx1,Tgx2]时,则Tg*=Tg.opt;
b)当Tg.optc)当Tg.opt>Tgx2时,则Tg*=Tgx2。
步骤6:根据最优梯次间隔,计算装备尽快形成梯次的预期梯次线。方法如下:
a)按下式计算理想梯次线,
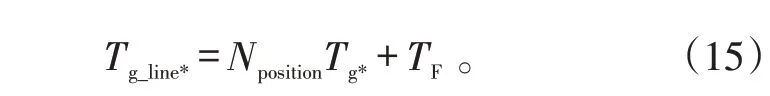
式(15)中:Tg_line*理想梯次线纵坐标;Nposition是梯次线横坐标;Tg*是计算得到的最优梯次时间;TF是装备翻修周期。
b)按下式计算基于实际寿命的梯次线偏离度:
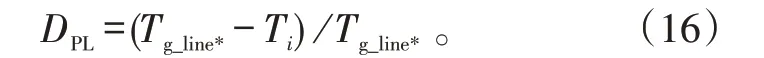
式(16)中:偏离度DPL表征梯次线偏离装备现有余寿线的程度。下面,将找到最大偏离点,并绘制梯次线。
c)计算最大偏离值和位置:

式(17)中:max()∙为MATLAB 程序中的计算最大值函数;max_PL 是最大偏离值;Xmax是最大偏离值对应的坐标。
d)采用平移法,计算预期梯次线:
过最大偏离点,计算理想梯次,相当于已知斜率过直线外一点,求直线。具体如下:

式(18)(19)中:bx_max为直线方程截距;Ti为飞机逐号余寿;Tg.line.opt为待绘制的预期最优梯次线。
3 算例
下面以1个算例说明本文模型及算法。算例需要的装备信息,如表2所示:
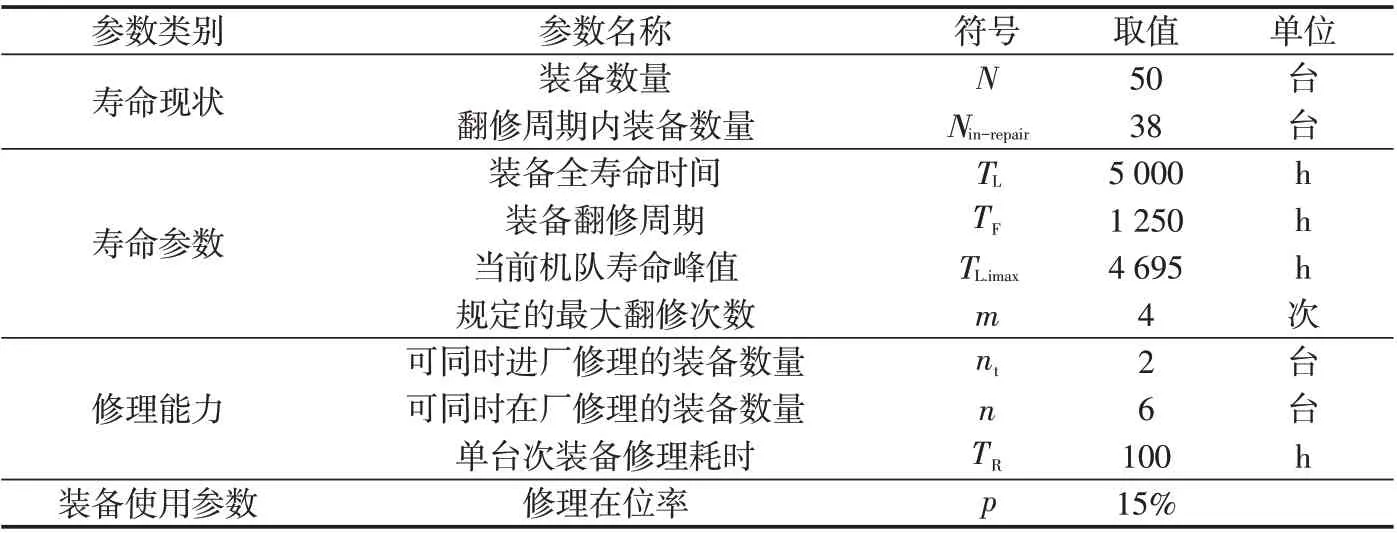
表2 装备信息表Tab.2 Basical information of the sample
随机设定一批装备寿命Ti,如表3所示。
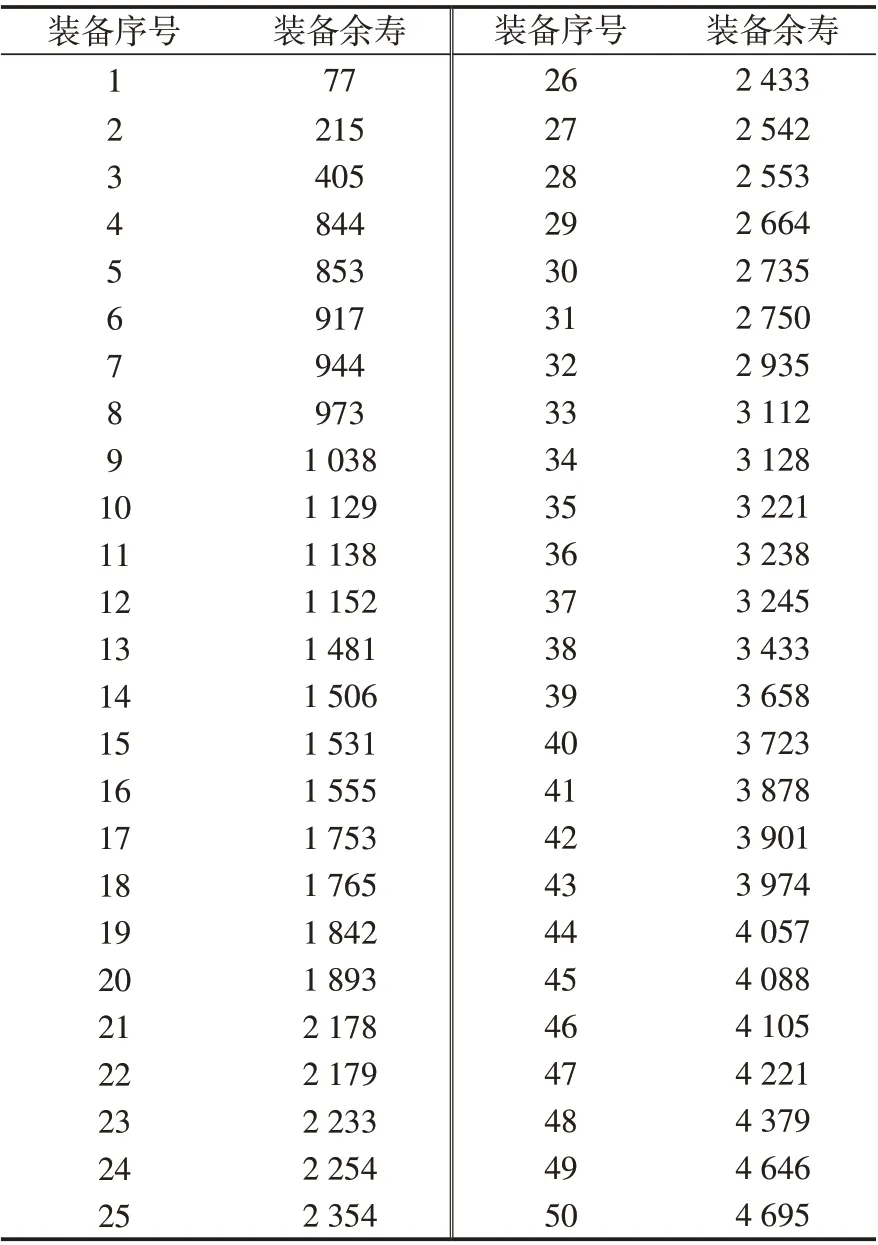
表3 装备寿命信息表Tab.3 Information of the equipment lifespan
1)按下式计算当前机队翻修周期内装备最大使用间隔:

3)比较Tgx1和Tgx2,此时Tgx1≥Tgx2,可进一步计算最优梯次间隔Tg.opt,经计算Tg.opt=86.78,此时计算得到的Tg.opt4)根据最优梯次间隔,计算装备尽快形成梯次的预期梯次线。为显示本发明效果,分别计算梯次Tg*=Tgx1=100 和Tg*=Tg.opt=86.78 的梯次线,如图7 所示:

图7 梯次线计算结果示意图Fig.7 Calculation results of the echelon interval time line
由上图可见,计算结果正确。当Tg*=Tg.opt=86.78时,装备可尽快形成梯次(圆形虚线位于三角形虚线上方)。但此时,已超出了大修厂的修理能力,同时在厂大修的装备数可由下式计算,其中,ceiling 意为向上取整。

经计算,这一情形下,大修厂需同时大修12 台装备才能满足梯次使用需要。 为此,应取Tg*=Tgx1=100。此时,大修厂同时大修6台装备,不仅符合修理能力客观要求,且装备也会尽快形成梯次。由此,次优解找到。
4 结论
本文针对装备使用中因梯次计划不合理,出现大修积压,影响了装备在位率,故无法满足装备使用需求的问题,综合考虑装备在位率要求、大修厂修理能力、装备实际余寿等各项因素,提出了一种装备使用最优梯次间隔计算方法,并通过算例进行了仿真说明。结果表明,本文方法可针对实际装备剩余寿命,给出最优梯次间隔时间参考建议,可为装备有序使用、避免出现大修积压、提高使用效率提供参考。
在修理时间TR
1)Tg≤TR
当Tg≤TR时,装备使用及修理情况,如图2 所示。即1号机使用TF后,进厂大修,修理时间为TR(阴影部分),由于此时装备进厂梯次间隔时间为Tg,因此,1号机尚未出厂,2号机进厂,将出现2架飞机同时在厂大修情况(TR重叠区域即为同时在厂时间)。如果修理厂修理线数量无法同时满足2 架飞机修理需要,就会出现飞机积压。因此,根据修理厂修理能力,对Tg进行推算。

图2 Tg ≤TR 的送修情形Fig.2 Condition of Tg ≤TR
假设大修厂同时在修的飞机数量最多不超过n台,每次同时进厂飞机数量为nt,则应存在如下关系:
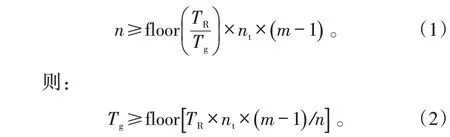
式(2)中:floor()∙是向下取整函数;m为最大翻修次数。
同时,积压的待修理飞机,也会影响部队的装备使用效率。假设部队共有飞机N架,规定的大修停飞率不大于p,则:
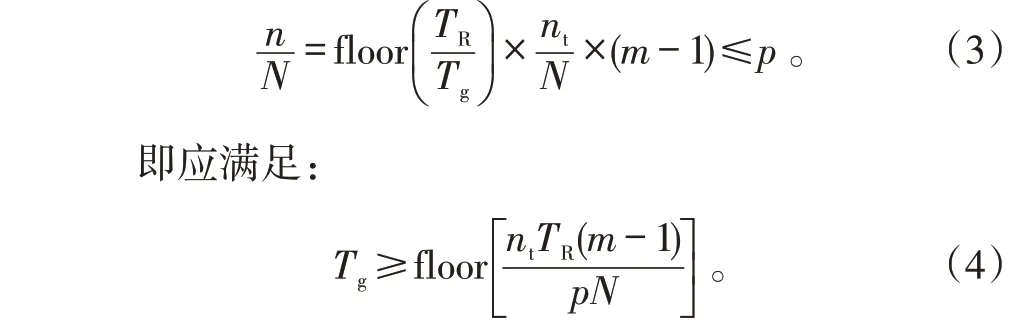
2)Tg>TR
当Tg>TR时,也可以形成梯次。这种情况如图3所示。其物理含义是前批飞机修理出厂后,后续飞机还没进厂,说明同时修理飞机数量就是单批次同时进厂飞机数量nt,因此,根据飞机在位率要求,有:

图3 Tg>TR 的送修情形Fig.3 Condition of Tg>TR

即:

这时,只要Tg≥TR,都可以形成梯次。
1.2 情形2:TR ≥TF
在修理时间TR≥TF时,区分Tg≤TR和Tg>TR2种情况进行讨论。
1)Tg≤TR
如图4 所示,前机没出厂,后机进厂,形成积压。同样,可根据修理能力对Tg进行推算,即修理能力限制下的梯次时间为:


图4 Tg ≤TR 的送修情形Fig.4 Condition of Tg ≤TR
2)Tg>TR
当梯次间隔时间Tg>TR,也可以形成梯次,如图5所示。这种情况下,前批飞机修理出厂后,后续飞机还没进厂,同样,只要满足nt≤pN且Tg>TR就可以形成梯次。

图5 Tg>TR 的送修情形Fig.5 Condition of Tg>TR
1.3 Tg 的上限分析
归纳1.1和1.2可以发现:

只要满足式(9),就可以形成梯次。但显然,Tg只能在一定范围内变化,如果Tg无限制增加,则无法使机队全部飞机形成梯次。因此,Tg还应满足以下关系:
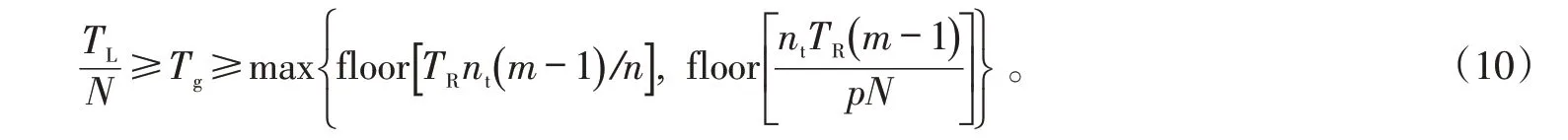
式(10)中,TL为装备全寿命时间。
1.4 梯次间隔时间数学模型小结
汇总以上各情形,如表1所示。

表1 梯次间隔时间模型归纳Tab.1 Summary of the echelon interval time model
2 最优梯次间隔时间算法
以上梯次间隔时间取值是1个区间范围。在实际使用中,装备使用者通常希望有1个最佳结果,以求使本单位装备尽快形成合理梯次。因此,本章主要针对实际装备寿命,建立最优梯次时间算法,进而为装备实际使用提供参考。具体算法,如图6所示。

图6 最优梯次间隔时间算法流程图Fig.6 Flowchart of the optimal echelon interval time algorithm
算法过程如下。

步骤1:按式(11)计算当前机队翻修周期内装备最大使用间隔,式(11)中:TL.imax指当前机队内剩余寿命峰值;Nin-repair指翻修周期内装备数量。
步骤2:按下式计算修理能力和装备在位率制约下使用间隔,

步骤3:判断Tgx1和Tgx2关系,当Tgx1 步骤4:当Tgx1≥Tgx2时,计算理想梯次间隔Tg.opt。方法如下: a)令待计算的理想梯次间隔时间为x,则此时的梯次线可用下式表示, 式(13)中:TF是装备翻修周期;Nposition是梯次线横坐标,对应了机队内飞机号码。具体如下: b)按下式计算装备余寿范数, 式(14)中:norm()∙为MATLAB 程序中的范数计算函数;Ti是Nposition对应的飞机当前剩余寿命;Tg_line_x是梯次线纵坐标。由于目的是使尽量多的装备尽快形成梯次,因此,采用了计算余寿平均二范数,并使用寻优求解的方法来计算梯次间隔。 c)判断y是否取得最小值,如果取得最小值,则此时的x即为待求最优梯次间隔时间,否则,继续更新x值,直到取得最小范数为止,则此时得到计算结果Tg.opt。 步骤5:根据计算结果,判断实际最优梯次间隔时间Tg*。具体判断方法如下: a)当Tg.opt在[Tgx1,Tgx2]时,则Tg*=Tg.opt; b)当Tg.opt c)当Tg.opt>Tgx2时,则Tg*=Tgx2。 步骤6:根据最优梯次间隔,计算装备尽快形成梯次的预期梯次线。方法如下: a)按下式计算理想梯次线, 式(15)中:Tg_line*理想梯次线纵坐标;Nposition是梯次线横坐标;Tg*是计算得到的最优梯次时间;TF是装备翻修周期。 b)按下式计算基于实际寿命的梯次线偏离度: 式(16)中:偏离度DPL表征梯次线偏离装备现有余寿线的程度。下面,将找到最大偏离点,并绘制梯次线。 c)计算最大偏离值和位置: 式(17)中:max()∙为MATLAB 程序中的计算最大值函数;max_PL 是最大偏离值;Xmax是最大偏离值对应的坐标。 d)采用平移法,计算预期梯次线: 过最大偏离点,计算理想梯次,相当于已知斜率过直线外一点,求直线。具体如下: 式(18)(19)中:bx_max为直线方程截距;Ti为飞机逐号余寿;Tg.line.opt为待绘制的预期最优梯次线。 下面以1个算例说明本文模型及算法。算例需要的装备信息,如表2所示: 表2 装备信息表Tab.2 Basical information of the sample 随机设定一批装备寿命Ti,如表3所示。 表3 装备寿命信息表Tab.3 Information of the equipment lifespan 1)按下式计算当前机队翻修周期内装备最大使用间隔: 3)比较Tgx1和Tgx2,此时Tgx1≥Tgx2,可进一步计算最优梯次间隔Tg.opt,经计算Tg.opt=86.78,此时计算得到的Tg.opt 4)根据最优梯次间隔,计算装备尽快形成梯次的预期梯次线。为显示本发明效果,分别计算梯次Tg*=Tgx1=100 和Tg*=Tg.opt=86.78 的梯次线,如图7 所示: 图7 梯次线计算结果示意图Fig.7 Calculation results of the echelon interval time line 由上图可见,计算结果正确。当Tg*=Tg.opt=86.78时,装备可尽快形成梯次(圆形虚线位于三角形虚线上方)。但此时,已超出了大修厂的修理能力,同时在厂大修的装备数可由下式计算,其中,ceiling 意为向上取整。 经计算,这一情形下,大修厂需同时大修12 台装备才能满足梯次使用需要。 为此,应取Tg*=Tgx1=100。此时,大修厂同时大修6台装备,不仅符合修理能力客观要求,且装备也会尽快形成梯次。由此,次优解找到。 本文针对装备使用中因梯次计划不合理,出现大修积压,影响了装备在位率,故无法满足装备使用需求的问题,综合考虑装备在位率要求、大修厂修理能力、装备实际余寿等各项因素,提出了一种装备使用最优梯次间隔计算方法,并通过算例进行了仿真说明。结果表明,本文方法可针对实际装备剩余寿命,给出最优梯次间隔时间参考建议,可为装备有序使用、避免出现大修积压、提高使用效率提供参考。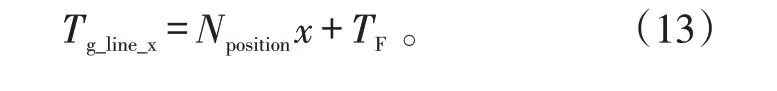
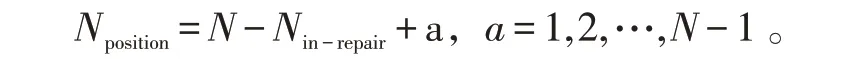
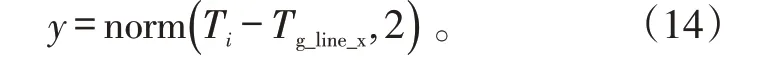
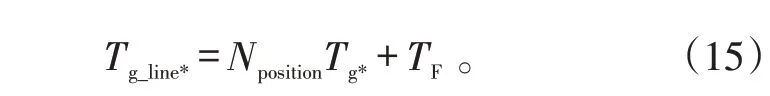
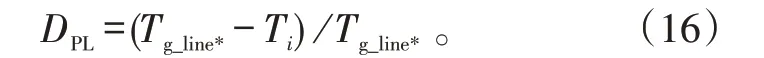


3 算例





4 结论
