“车-电-路-站”互联下电动出租车换电需求预测及换电站充电优化策略

傅质馨，朱韦翰，朱俊澎，袁 越，冯寅烁，王 鹤

（1. 河海大学 能源与电气学院，江苏 南京 211100；2. 河海大学 可再生能源发电技术教育部工程研究中心，江苏 南京 211100；3. 国网（北京）综合能源规划设计研究院有限公司，北京 100052）

0 引言

充电时间长是制约电动汽车产业发展的主要因素之一［1］，过长的充电时间缩短了电动出租车ET（Electric Taxi）的运营时间，间接地减少了其运营收入。对于ET这种具有快速电能补充需求的车辆，已有相关研究主要从快充和换电两方面开展。国家电网、特锐德、Tesla 等公司的快充网络正在逐步建立，极大地加快了充电速度，但其充电功率较大［2］，例如：Tesla V4 超级充电桩的充电功率达到350 kW，对电网的冲击较大。同时，快充用户的充电优先级较高，很难从时间尺度上对其进行调控［2-3］。“车电分离”后的换电模式能够很好地解决上述问题，部分公司如蔚来、北汽新能源等也逐渐开展了换电业务。《新能源汽车产业发展规划（2021—2035 年）》也指出应大力发展换电，为换电模式的研究提供了技术和政策支撑。

目前，针对换电模式的研究主要分为换电需求分析、换电站容量配置、换电站优化运行3 类。在换电需求分析方面：文献［4］考虑换电储备阈值对电动汽车换电需求规律的影响，为换电站电池储备决策、充电策略等提供了参考；文献［5］提出了电动汽车换电充裕度的概念，通过分析换电需求发生时刻得到不同时段的换电需求分布，并指出不合理的充电管理策略会导致负荷尖峰的产生，加剧电网负荷压力。但文献［4-5］均未从路网、选站决策的角度对换电需求进行分析。文献［6］采用深度优先搜索算法和出行链为电动汽车规划一天的行驶路径，充分考虑了路网结构、路径选取对换电需求的影响。但文献［4-6］缺乏对ET 规律性换电需求及充电调控的研究。在换电站容量配置方面：基于“即充即换”的运行策略，文献［7］计及服务可用性进行换电站容量优化配置，但与“换电站可作为储能资源，具有可调控功率”的观念相冲突；文献［8］对电池配送方案和集中充电站容量规划进行了联合优化，指出配送方案对充电站经济性、充电方式对充电站容量规划的重要作用。在换电站优化运行方面：文献［9］分析了电动汽车充放储一体化充换电站为电网提供削峰填谷服务的能力；文献［10］提出了一种运营利润最优的模块分割式换电站有序充电模型；文献［11］建立了换电站的日前调度与实时调度模型，在避免电池缺额的同时优化电网的运行；文献［12］以投入充电的电池数量为控制变量建立有序充电模型，并提出了一种基于量子策略的改进布谷鸟算法用于快速求解模型。然而，文献［9-12］的研究对象主要是电动私家车，这类电动汽车对换电模式的兼容性较差，同时研究中脱离路网，对电动汽车的出行行为研究不足。

从电池兼容性及车辆统一管理的角度考虑，换电模式更加适用于ET。基于上述对换电模式研究成果及不足的分析，本文以ET 为研究对象，充分考虑交通、电力、信息通信系统对规律性换电需求和充电负荷的影响，强调ET、电池与上述系统间的紧密联系，对“车-电-路-站”互联下的换电需求预测及换电站优化运行进行研究。首先，提出了基于换电模式的“车-电-路-站”互联系统模型，阐述了其闭环运行模式；然后，提出了换电式ET模型，并对其站内、站外行为进行研究，分析了换电站的“用户链-电池链”交互运行模式、各时段的电池状态；最后，提出了换电站高峰储能利用率的概念，在满足换电需求的前提下，以一种考虑平抑负荷波动和提高储能利用率的两阶段优化策略，安排典型换电式ET的电池充电计划，充分发挥换电站电池的可控、储能特点。

1 基于换电模式的“车-电-路-站”互联系统模型

基于换电模式的“车-电-路-站”互联系统描述了换电式ET、电池、路网、换电站这4 个主体之间的互动关系，系统框架如图1 所示，主要包括以下4 个交互过程。

图1 “车-电-路-站”互联系统框架Fig.1 Framework of“ET-battery-traffic-swap station”interconnection system

1）ET 和路网的交互：对于没有换电请求的ET而言，其可在订单平台不断发布需求并接收系统派送的订单，在载客状态和空载寻客状态之间不断变换；而对于具有换电请求的ET 而言，其需要退出出租运营，进行选站和路径规划，前往适合的换电站进行电能补充。该交互过程在能量流上体现为电池电量的不断衰减。

2）ET 和换电站的交互：根据ET 的到站时间及站内排队、储备电池数量的情况确定是否开始换电或者等待换电，换电完成的ET离站后即刻开始出租运营。

3）ET 和电池的交互：ET 卸下电池，并装载上换电站内存储的满电电池。该交互过程可以看作是“车电分离”，有2 层含义：①用户车辆和电池相分离；②用户和电池充电所有权相分离，由换电站统一管理。

4）电池和换电站的交互：换电站可以在满足后续换电需求的前提下，充分发挥其充电积极性，结合电网的运行条件等进行有序充电。

前3 个交互过程可看作用电部分，包括ET 运行消耗电能、ET 与电池分离、ET 进行换电装载新的电池，第4 个交互过程可看作充电部分，主要用于安排电池充电。因此，互联系统的4 个交互过程形成了一个基于信息流-能量流-交通流的“用电-充电”闭环系统。

2 “车-电-路-站”互联下日前换电需求模拟预测

根据ET 的出行、选站及换电行为，对多信息互联下的ET 行驶路径、运营状态、电池荷电状态SOC（State Of Charge）进行模拟，计算得到换电站在各调度时段初始时刻为满足ET 的正常运营所提供的电池数量，即为“车-电-路-站”互联下的换电需求。

2.1 换电式ET模型

日常运营的换电式ET 具有较强的连续行驶行为，与交通路网的联系紧密，本文所用交通路网模型参考文献［13］。换电式ET 和换电站的交互过程仅为电池更换，不涉及充电部分，故不会直接影响充电负荷大小。

2.1.1 换电式ET的出行行为建模

换电式ET具有连续行驶行为，且其出行目的地具有较强的随机特性［14］，在日常运营的过程中存在载客、空载寻客、空载换电这3 种状态，三者之间的转换关系见附录A图A1，具体描述如下。

1）载客状态。在该状态下，ET 根据乘客偏好以打车费用最少或行驶时间最短为目标，采用Dijkstra算法进行路径规划。

2）空载寻客状态。ET 结束载客后开始寻客，已有研究主要根据起讫点（OD）矩阵确定其行驶行为［14-15］，OD 矩阵反映的是某地对ET 当前所处位置的吸引能力，但若所有ET 都向OD 概率高的地方聚集，则会降低接客的可能性。结合文献［14］中的OD概率矩阵，本文提出了一种考虑各区域出租车占比的空载寻客概率模型。假设ET 当前处于区域i，则t时段ET选择区域j作为寻客地点的概率p(i，j，t)为：

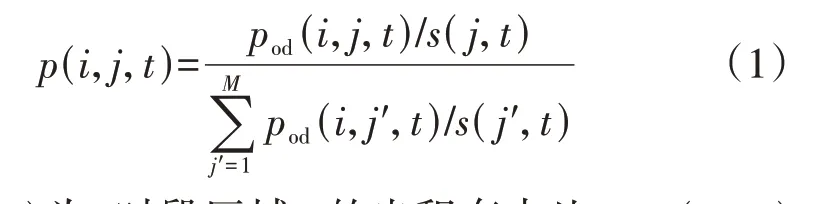
式中：s(j，t)为t时段区域j的出租车占比；pod(i，j，t)为t时段出租车从区域i行驶到区域j的OD 概率；M为区域数量。p(i，j，t)与pod(i，j，t)成正比，并且与s(j，t)成反比，这反映了区域内出租车供需关系的平衡情况。

3）空载换电状态。当ET 的电池电量低于一定的阈值时，ET 将结束运营进程，综合考虑前往换电站的时间、排队时间和从换电站前往下一最佳寻客点的时间，在电量能满足行驶距离需求的前提下选择最佳换电站进行电能补充。由于换电时间较小且差异不大，本文不考虑换电时间差异性对总时间的影响。则选择换电站k时考虑的总时间Tall，k(t)为：

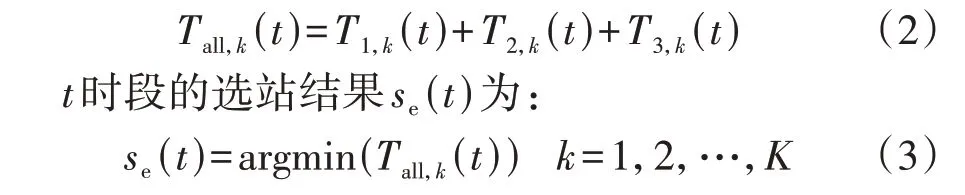
式中：T1，k(t)、T2，k(t)、T3，k(t)分别为t时段ET 前往换电站k的时间、在换电站k的排队时间、从换电站k前往下一最佳寻客点的时间；K为换电站数量。

2.1.2 换电式ET的换电行为建模

1）换电需求。

当t时段电池的荷电状态SSOC(t)不高于0.2［14］，即满足式（4）时，产生换电需求。

2）换电时间。

换电时间Tswap一般为3～5 min［16］，故换电式ET的电能补充时间大幅缩减，可增加运营时间以获取更多的收入。

2.2 换电站站内行为分析

2.2.1 假设条件

1）对于在t时段未换电成功的ET而言，其在t+1时段初优先进行换电；

2）处于排队队列的ET根据到站时间的先后，在每个时段初安排换电；

3）由于换电时间较短，对站内行为分析的时间进行离散化，设置单个时段时长为5 min。

2.2.2 站内行为分析

站内行为示意图见图2，由t-1、t、t+1 这3 个相邻时段组成。图中：以t时段为例说明，τt，0、τt，1分别为t时段的起始时刻、结束时刻，t时段的起始时刻为上一时段的结束时刻，即τt-1，1=τt，0，其他类似；虚线①、②均表示τt，0—τt，1时段内到达换电站且可在该时段成功完成换电的ET的时间跨度，不同之处在于虚线②表示ET行程的起始时刻在τt-1，0之前，成功换电的ET将于τt+1，0时刻离站开始出租运营；实线③表示τt，0—τt，1时段内到达换电站但无法在该时段完成换电的ET，这部分ET进入排队队列，在τt+1，0时刻根据排队队列安排是否换电。计算t时段成功完成换电的ET 数量，即为t时段换电站的换电需求U(t)。需要说明的是，换电需求U(t)指的并不是t时段站内、站外电池电量不足的ET总数量，而是t时段换电站应提供换电服务的ET数量，受到换电设备数量的影响。

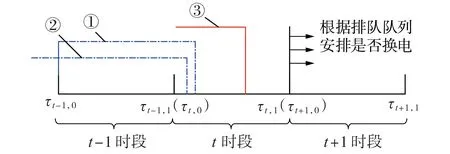
图2 站内行为示意图Fig.2 Schematic diagram of ET behaviors in station

3 换电站“用户链-电池链”交互运行模式及电池状态分析

换电站的主要功能包括提供换电服务和充电管理［11］。“车电分离”后换电站拥有对电池充电管理的权力，可以在只考虑储备电池满足换电需求的约束条件下，结合电网的运行水平对电池组集群进行充电。

3.1 “用户链-电池链”交互运行模式

“用户链-电池链”交互运行模式如图3 所示，其主要包括用户链、电池链2 个部分，两者既是2 个独立的闭环系统，又可通过换电平台进行交互，在2 个闭环系统之间进行能量传递。

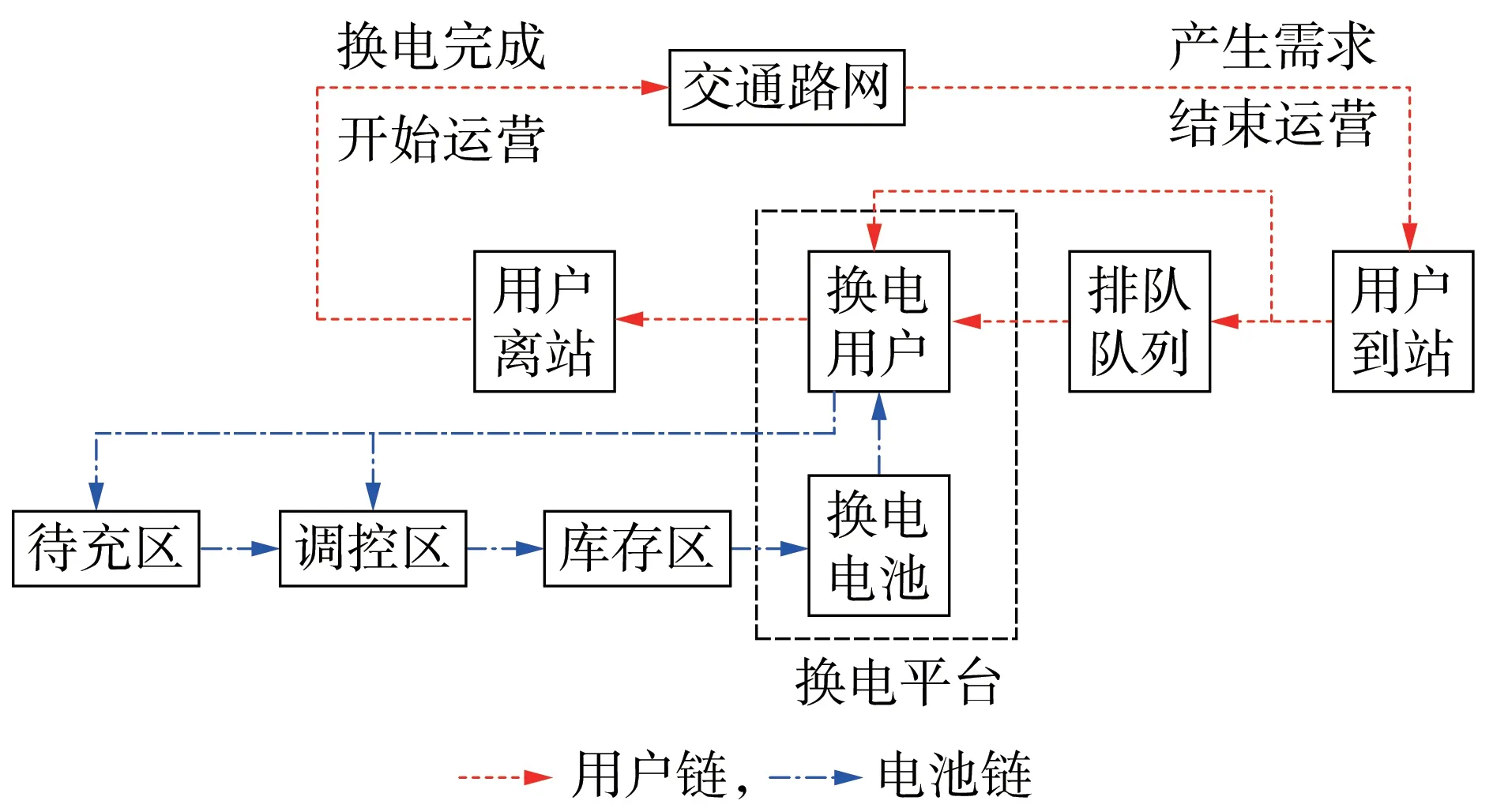
图3 “用户链-电池链”交互运行模式Fig.3 Interactive operation mode of“user chain-battery chain”

1）在用户链方面，若交通网中处于运营状态的ET 一旦产生换电需求，则结束运营，选择合适的换电站进行电能补充；到站用户根据排队队列情况进行排队等待或更换电池；在完成电池更换后，用户即可离站，开始新的运营过程。

2）在电池链方面，主要分为待充区、调控区、库存区、换电平台4 个部分，换电用户更换下来的电池立即进入待充区，待充区电池根据调控方法的不同不断地定期投入调控区进行充电，充电结束的电池进入库存区等待换电，换电平台负责调取库存区电池为用户进行换电。

3.2 假设条件

1）t时段更换下的电池进入待充区，可在t+1 时段投入充电；

2）t时段内刚充满电的电池进入库存区，可在t+1时段用于换电。

3.3 换电站内电池状态分析模型

电池链内的电池具有不同的状态，本文将电池分为待充电池、投入电池、在充电池、产出电池、储备电池5 类，基于此建立换电站内电池状态分析模型。t时段初换电站可提供的储备电池数量Ns(t)为：

Ns(t)=max{0，Ns(t-1)+y(t-1)-U(t-1)} （5）

式中：y(t-1)为t-1 时段的产出电池数量，这部分电池在t-1 时段结束充电，并可在t时段初提供换电服务；U(t-1)为t-1时段的换电需求。

为了简化分析，本文假设定期向调控区投入一定数量的电池，t时段初投入电池数量的最大值xmax(t) 受t-1 时段末未连接电池的充电桩数量Nr(t-1)和t-1 时段末待充电池数量Nw(t-1)影响，见式（6）。

t时段末未连接电池的充电桩数量Nr(t)受充电桩总数量Nall、t时段在充电池数量Nc(t)和t时段末产出电池数量y(t)影响，如式（7）所示。

t时段末产出电池数量y(t)与t时段初投入电池数量x(t)具有一定的制约关系，可以用复合函数表示为：

式中：f表示y(t)与x(t)之间的对应关系。

所有更换下来的电池都需进入待充区，然后等待定期调度决定是否投入调控区充电，则t时段末待充电池数量Nw(t)为：

本文认为换电站在新的一天运营开始前初始储备电池都处于满电状态，数量记为NB，则t时段初换电站内的电池应满足如下平衡关系：

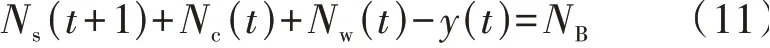
4 换电站的高峰储能利用率

当电网负荷处于高峰时段时，有序充电模式下换电站内的储备电池能够对高峰负荷进行一定的消纳，本文从多余储备电池数量的角度定义换电站高峰储能利用率如下：

式中：ηpeak(t)为t时段换电站的高峰储能利用率；Nsdd(t)、Nsod(t)分别为t时段无序、有序充电模式下的多余储备电池数量；Nsd(t)、Nso(t)分别为无序、有序充电模式下t时段初的储备电池数量。当换电站采用无序充电模式时，有Nsdd(t)=Nsod(t)，此时的高峰储能利用率ηpeak(t)=0。

Nsdd(t)、Nsod(t)反映的是换电站的剩余储能能力大小，这部分电池没有被利用，在调控状态下Nsod(t)越小，表明储能利用率越高。换电站的剩余储能能力示意图见图4。图中：黑色和灰色区域表示无序充电模式下换电站的可调控总储能容量，即Nsdd(t)块多余储备电池；黑色区域表示某种调控策略下换电站的可调控总储能容量，即Nsod(t)块多余储备电池；灰色区域表示在某种调控策略下已经被调用的储能容量，即Nsdd(t)-Nsod(t)块多余储备电池。可看出，在特定的调控策略下，换电站的储能能力仍可进一步开发，从而为电网提供其他辅助服务功能。换电站的可调控储能容量主要受充电功率、总储备电池数量的影响，其中充电功率影响库存区补充满电电池的速度，总储备电池数量影响换电站的总容量。

图4 换电站的剩余储能能力Fig.4 Residual energy storage capacity of swapping station

非快速电能补充的电动汽车具有较强的时间可控性，已有文献针对其移动及储能特性进行了虚拟电厂容量评估、优化等方面的研究［17］。但是采取快速电能补充的电动汽车的时间可控性较差，其很难作为一种可控储能资源，而以“车电分离”的换电模式作为快速电能补充方式为电动汽车参与储能调度提供了一种可能性，在该方式下换电站内的储备电池失去了空间转移特性，但仍受电动汽车出行行为的影响，具有间接的移动特性。

则换电站的综合利用率η可表示为：

式中：t1、t2分别为高峰起始时段、结束时段。

5 基于日前需求预测的换电站充电优化策略

通过多次仿真取平均值的方式得到ET 的日前换电需求，并以此为基础对换电站电池进行充电优化。

5.1 假设条件

本文参考文献［12］做出如下假设：

1）统一化电池规格，采用市面上换电式ET广泛采用的车型北汽EU300，电池容量为45 kW·h；

2）充电功率恒定且不可中断；

3）为了保证准确性并减少维数增大对计算的影响，对充电时段进行离散化，设置单位时段跨度Δt为15 min。

5.2 优化目标函数

为了充分发挥具有强出行特性的ET 快速电能补充对削峰填谷、平抑负荷波动的作用，同时提高储能利用率，发挥储能对换电需求的缓冲能力，本文提出了一种两阶段日前优化策略。在阶段1 以平抑负荷波动为目标：

式中：F1为阶段1 的目标函数值；Pl(t)为t时段的区域负荷；Pc为单个充电桩的充电功率；T为优化周期离散后的时段数量；Pav为优化周期内负荷的平均值。

将阶段1的优化结果作为阶段2的约束条件，并以换电站的综合利用率最大作为阶段2的目标：

式中：F2为阶段2的目标函数值。

5.3 约束条件

1）t时段初投入电池数量x(t)应不小于0，即：

2）t时段初投入电池数量x(t)应不大于t-1时段末待充电池数量Nw(t-1)和未连接电池的充电桩数量Nr(t-1)，即：

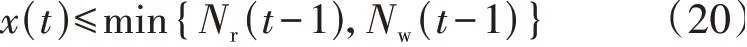
式（20）表示投入电池数量x(t)的上限约束，描述了t时段初换电站最多可以投入的待充电池数量。

3）t时段初，应保证储备电池量Ns(t)不小于换电需求U(t)，即：

考虑到ET在一天中具有多次换电需求，即换电需求较强，本文参考文献［12］设置充电桩的充电功率为40 kW，经仿真可知ET 替换下来的电池平均荷电状态为0.107，因此设置电池组接入充电设备的时长为4Δt，补充电池电能至额定容量的90%，则式（9）可改写为y(t)=x(t-3)，进而式（24）可简化为：

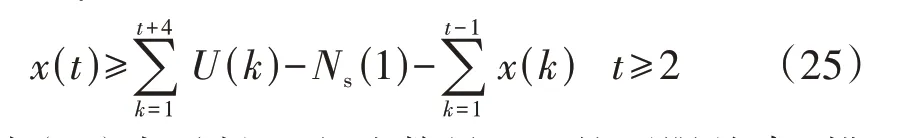
式（25）表示投入电池数量x(t)的下限约束，描述了为了满足换电需求，当前时段换电站至少要投入的待充电池数量，其主要受换电需求的影响。由于初始时段待充区的电池数量为0，所以x(1)=0。

4）换电站的充电优化是在优化周期内合理地将充电电量分配至各个时段，优化前、后的总充电电量不变，即：

式中：Et为优化后t时段的充电电量；Esum为总充电电量。

5）在新的一天运营周期开始前，应保证换电站内的所有电池满电。

6 算例仿真分析

6.1 参数设置

本文的交通路网拓扑结构见附录A 图A2，其中各道路的长度、承载量及功能区分区情况参考文献［13］，共设置5 座换电站（S1—S5），S1—S5分别位于交通路网的节点6、7、13、17、26，各换电站配置10台换电设备。假设该区域有1 000 辆换电式ET，单位能耗为0.23 kW·h／km。根据文献［18］中储备电池数量与ET 换电需求之比为0.6∶1，设置储备电池数量为600 块。根据文献［11］中储备电池数量和充电桩数量之比为3∶2，设置充电桩总数量约为400 台。每座换电站的储备电池数量和充电桩数量见附录A图A3。ET 在06:00—09:00 时段逐渐接入互联系统，在21:00—24:00时段内逐渐从互联系统中退出，电池的初始荷电状态服从0.5～0.8 范围内的均匀分布。区域电网的基本负荷曲线见附录A图A4。

6.2 换电需求分析

假设1 辆ET 在换电站内更换1 块电池（电池容量为45 kW·h），根据第2节的分析，可得总换电需求和各换电站的换电需求如图5 所示。由图可知：在空间维度上，各换电站的换电需求大小及其变化趋势不尽相同，说明换电站的地理位置分布会对换电需求产生一定的影响；在时间维度上，不管是区域总换电需求，还是各换电站的换电需求，均大致呈波浪形，具有周期性特点，这主要是受到ET 连续“运营-换电”进程的影响，同时各换电站换电需求峰值在时间维度上也具有差异性，最为显著的是S3和S5，S3的换电需求峰值具有“两边大、中间小”的特点，S5在15:00—18:00时段的换电需求峰值最大，这与“商业区逐渐进入营业高峰时段，ET 司机有更大的概率在商业区进行运营并就近换电”的实际情况相符合。

图5 换电需求结果Fig.5 Battery swapping demand results

6.3 换电站无序充电模式分析

无序充电（“即换即充”）模式下换电站的总充电负荷和各换电站的充电负荷见图6。由图可知，总充电负荷和各换电站的充电负荷与其对应的换电需求变化趋势相类似，且略微滞后于换电需求。根据ET的运营特点，总充电负荷有非常明显的4个高峰，在高峰之间有相对较小的负荷低谷，最大峰谷差值为4.4 MW，为最大峰值的28.87%，可见如何利用负荷峰谷之间的关系，配合区域负荷对各时段的电池充电计划进行合理规划，以达到削峰填谷和平抑负荷波动的作用，是换电站有序充电需解决的问题。

图6 无序充电模式下的充电负荷Fig.6 Charging load under disordered charging mode

6.4 换电站有序充电模式分析

在区域电网基本负荷的基础上，叠加无序和有序充电负荷后的总负荷曲线如图7 所示。由图可知，叠加无序充电负荷、阶段1 有序充电负荷和阶段2 有序充电负荷后总负荷的峰谷差分别为50.724 3、41.3726、41.2126 MW，目标函数值F1分别为2.9340×104、2.4042×104、2.4039×104MW2，有序充电优化后阶段1、2 的负荷峰谷差分别减小9.351 7、9.511 7 MW，相比无序充电模式，峰谷差率分别减小了18.44%、18.75%，两阶段优化后F1相比无序充电模式改善了18%。可见有序充电负荷能够充分发挥储备电池的缓冲作用：在高峰时段减少投入电池的数量，降低09:00—12:00 和17:00—21:00 这2 个高峰时段的负荷，且对09:00—12:00时段的负荷削峰作用较明显，经有序充电优化后阶段1、2 相较于无序充电模式的最大削峰量分别为6.40、6.44 MW；同时在白天的低谷时段增大投入电池的数量，使得12:00—16:00 时段的负荷有所提高。ET 在24:00 结束运营后，换电站不再有换电需求，此时库存区储备电池数量维持在一个较低的水平，而待充区电池数量维持在一个较高的水平，可在24:00 至次日06:00 的凌晨低谷时段安排这部分电池进行充电，从而达到削峰填谷、平抑负荷波动的效果。

图7 叠加无序和有序充电负荷后的总负荷曲线Fig.7 Total load curves with disordered and ordered charging load

6.5 高峰储能利用率分析

无序充电模式和阶段1、2 有序充电优化后各换电站的多余储备电池数量（储备电池数量与换电需求之差）变化曲线见附录A 图A5。由图可知，在09:00—12:00 和17:00—21:00 这2 个负荷高峰时段，有序充电模式下的多余储备电池数量有所减少，表明在这2 个时段内储备电池具有缓冲作用，在保证不多投入电池充电的情况下消纳部分换电需求。不论是在有序充电模式下，还是在无序充电模式下，S5在17:00—18:00 时段内的多余储备电池数量小于0，这种情况表明该时段内S5内的储备电池并不能满足换电需求，会影响换电站的正常运营，ET 需花费额外的等待时间进行换电，若要消除这种情况，则需增加储备电池数量或充电桩数量。在有序充电模式下，大约20:00之后各换电站的多余储备电池数量为0，表明各时段初的储备电池数量正好能满足该时段的换电需求，调控区产出满电电池的速度能够有效地跟随换电需求，保证更多的待充电池能够在填谷时段进行充电。可见，换电站的调控能力受换电站内电池总数量的影响，电池总数量越大，则换电站的调控能力越强，削峰填谷的效果越好。

10:00—21:00 时段内阶段1、2 优化后的高峰储能利用率如图8所示。由图可知，在10:00—21:00时段内，阶段1 优化后S1—S5的平均储能利用率分别为44.39%、29.41%、45.41%、30.48%、41.95%，阶段2优化后S1—S5的平均储能利用率分别为49.04%、33.21%、53.55%、30.48%、41.95%，可见阶段2 优化改善了S1—S3的储能利用率情况，改善程度分别为10.48%、12.92%、17.92%。S1—S3在阶段1、2 的高峰储能利用率对比见附录A 图A6。S4、S5主要受换电需求和储备电池总数量的影响，阶段2 的储能利用率在不影响阶段1 负荷平抑效果和负荷峰谷差的前提下，并没有得到提高。经两阶段优化后，换电站的储备电池发挥了一定的储能作用，削减了负荷高峰。可以发现，在19:00 之后，换电站的储能利用率维持在一个较高的水平，甚至出现利用率为100%的情况，这是因为换电站可以根据换电需求，提前一个充电周期将最少量的待充区电池投入调控区进行充电，实现电池“产出-消耗”的平衡。同时待充区电池数量可维持在较高的水平，等待一天中的负荷低谷时段投入充电，起到提高谷时段负荷的作用。

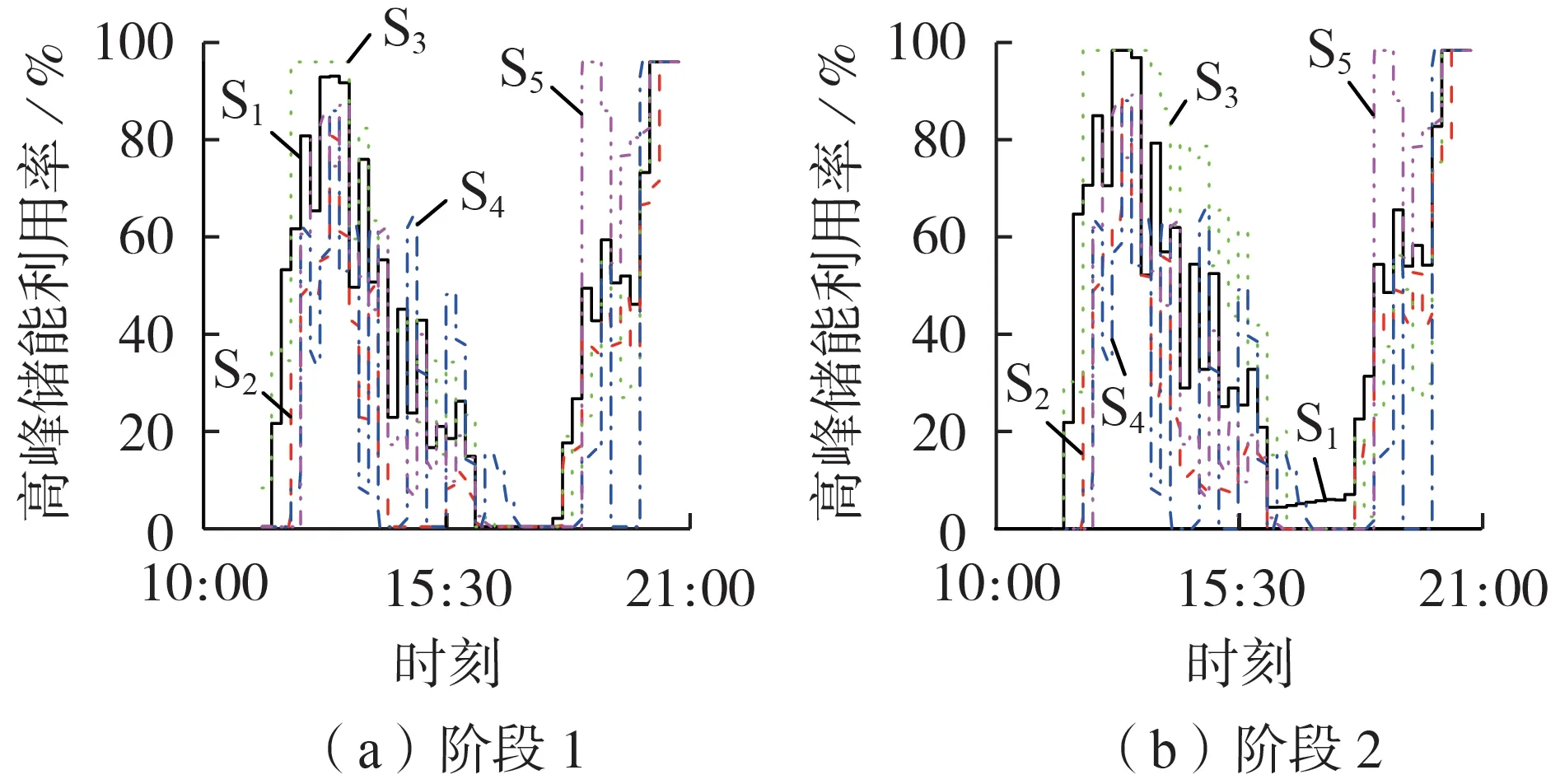
图8 优化后的高峰储能利用率Fig.8 Optimized peak energy storage utilization rate

7 结论

本文基于换电模式下的“车-电-路-站”互联系统，首先结合交通路网、ET 的时空特性，对ET 的日前换电需求进行预测，揭示其波浪形变化趋势的特点；然后根据“用户链-电池链”交互框架分析换电站内的电池状态变化和ET行为；最后以平抑负荷波动为目标对换电站内电池的充电计划进行规划，以充分发挥换电站的储能特性及“车电分离”后的电池可控性，以换电模式作为ET 的快速电能补充方式之一，有效解决快速充电在时间尺度上的不可控性问题。算例仿真结果表明，本文所提优化策略能起到平抑负荷波动、削峰填谷的作用，并能发挥换电站的储能利用效果。

随着政策和换电技术的不断发展，换电模式在未来扮演着更加重要的角色，考虑日内实时换电需求偏差控制与充放电策略的联合优化，以及考虑多元因素的储能利用率评估方法将是下一步的研究重点。

附录见本刊网络版（http：//www.epae.cn）。