电力现货市场环境下电动汽车充换电站的优化调控策略

2022-10-15曾宪锴刘璐瑶谭俊丰

电力自动化设备 2022年10期

曾宪锴，杨苹，刘璐瑶，杨康，谭俊丰

（1. 华南理工大学电力学院，广东广州 510640；2. 华南理工大学广东省绿色能源技术重点实验室，广东广州 510640）

0 引言

在构建新型电力系统的战略目标下，电动汽车EV（Electric Vehicle）充换电站BCSS（Battery Charging and Swapping Station）等需求侧资源在参与电力系统的实时平衡调节中将扮演越来越重要的角色［1］。在电力现货市场环境下，利用站内冗余电池作为调节资源，通过优化调控策略充分挖掘BCSS的调节潜力，参与多种交易品种以提升BCSS的经济效益，为新型电力系统建设提供支撑。

目前，关于BCSS优化调控策略的研究大多集中在电能量市场环境下的充电管理、与新能源发电的协同运行等方面。文献［2-3］分别分析了电池折旧和备用电池数量等因素对充电成本的影响，并形成相应的充电策略，实现了投资成本与运营成本统一考量下的优化调控。为进一步挖掘优化空间，文献［4-5］对电池的可调节性和各类充电机的特性进行建模，通过机器学习和智能算法求解调控策略。与新能源发电的协同运行方面，需要充分考虑新能源发电、换电需求、电价等多重不确定性，文献［6］在场景规划中加入风险测度以量化多类型不确定性带来的风险；文献［7］利用概率性序列描述系统的不确定性，采用机会约束规划求解调控策略，从而消除不确定性对策略有效性的影响。

随着电力体制改革不断深入，辅助服务交易推广至需求侧［8］，为EV 等可调资源带来新的盈利点，其关键问题在于电池资源聚合、响应能力预估、响应功率分配等。文献［9］研究EV参与辅助服务的可支配容量预测与聚合模块开发，有效解决了车网互动（V2G）聚合调控问题；文献［10］提出采用EV、储能和光伏发电系统联合调峰的方法，显著降低了区域能耗及用能成本，并在此基础上展望更利于电池储能参与电力系统调节的市场机制；文献［11-14］针对EV参与调频辅助服务，从集群、自动发电控制（AGC）、功率分配等环节分别展开研究，提出相应模型和控制策略以提高其经济效益；文献［15］考虑电价和调频指令的不确定性，提出基于调频绩效考核的EV鲁棒控制模型，增强了EV作为需求侧资源的可靠性。

上述研究从多维度分析了BCSS 参与电力市场各交易品种的优化调控策略，但对于电力现货市场环境下BCSS参与多电力交易品种的调控研究较少。而随着新型电力系统逐步构建，电力现货市场逐步发展，BCSS 未来将面向能量-辅助服务的多交易品种环境，对其规模化支撑电网实时平衡的能力提出新的需求和要求。为此，本文提出协同参与电能量交易、调频辅助服务交易和多阶段需求响应交易的BCSS 优化调控策略。为全面反映BCSS 换电服务和现货市场多品种交易的协同开展状况，提出可精确描述电池在换电、充电、放电、满电状态之间转换的换电行为约束，建立日前鲁棒优化-日内基于模型预测控制MPC（Model Predictive Control）的滚动优化-实时优化调控的BCSS 多阶段优化调控策略。在此基础上，分析多阶段需求响应价格与时段对调控结果的影响，探讨不确定度控制系数和收益权重系数对BCSS运行收益的影响，从而在计及市场需求和价格的不确定性下充分发挥电池的盈利能力，为电力现货市场环境下的BCSS 提供更加经济高效的运营模式。

1 电力现货市场环境下EV BCSS的调控模型

根据南方电力现货市场系列试点规则方案，提出电力现货市场环境下BCSS 可参与的交易品种及其特点，明确BCSS调控流程，并建立其调控模型。

1.1 EV BCSS参与的电力交易品种

随着EV 换电模式的发展，BCSS 的建设规模和用电量不断增长，大规模BCSS可满足电力批发市场准入条件，直接参与市场交易，小规模的BCSS 则可以通过聚合的形式间接参与。对于满足准入条件的BCSS 或BCSS 聚合体，总结其在电力现货市场环境下可参与的交易品种及其特点，具体如下。

1）需求响应：日前-日内-实时多时间尺度开展。日前及日内阶段采用邀约响应形式，在响应时段的前1 d 或前4 h 发布响应邀约，需求侧竞价确定计划响应量并在响应时段执行。实时阶段采用实时响应形式，需求侧需在收到响应需求后5 min达到响应目标，并可出于安全性或经济性考虑改变响应状态。

2）调频辅助服务：优质调频资源优先调用机制。调频市场成员完成调频里程价格及调频容量申报后，将根据各成员近期的综合调频性能调整其调频里程报价，使得优质调频资源优先被调用。

3）现货电能量交易：申报偏差收益转移机制。电能量交易经历日前与实时2 个阶段。日前市场用于市场成员申报，出清结算中标购售电曲线；运行日内实时市场基于实际运行情况再次计算调整，并根据市场成员实际购售电与日前中标曲线的偏差进行结算。

1.2 电力现货市场环境下EV BCSS调控架构

EV 换电模式分为电池配送模式和换电站模式［16］，本文以电池配送模式为研究对象，建立电力现货市场环境下BCSS的调控架构，如图1所示，图中ns为电池配送站总数。BCSS 为电池充电，并将就绪的电池统一配送至电池配送站；EV 通过电池配送站缴纳换电服务费用并获取换电服务。同时BCSS 参与电力现货市场获取收益，包括电能量交易、调频辅助服务交易及多时间尺度的需求响应交易。

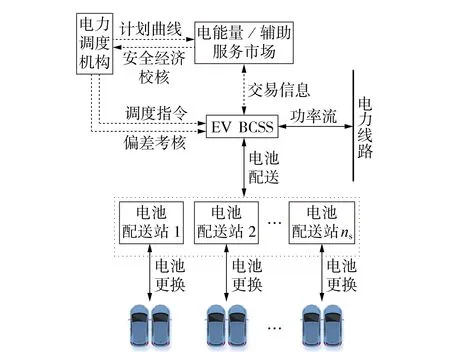
图1 电力现货市场环境下BCSS的调控架构Fig.1 Regulation structure of BCSS under electricityspot market environment

为确保BCSS 开展换电业务的同时参与电力现货市场获取收益，需从日前、日内、实时3 个阶段进行优化调控，其调控流程见附录A图A1。

日前阶段，BCSS 运营商接收需求响应日前邀约和调频市场信息，结合次日换电需求预测曲线，决策购售电曲线、日前需求响应曲线、调频容量和换电计划，本阶段决策中考虑换电需求、调频调用电量和各交易品种价格的不确定性，需预留一定的电量裕量，以确保其各项业务稳定开展，同时也为日内和实时阶段的优化调控预留了可调空间。日内阶段在日前优化结果的基础上开展滚动优化，接收需求响应日内邀约，结合日内换电需求预测值，决策日内需求响应曲线、调整购售电曲线和换电计划，本阶段决策中已明确各电力交易品种的日前出清价格，且日内短周期的换电需求预测结果更加准确，因此日前预留的电量在本阶段可被较充分利用。实时阶段基于日内优化结果对充放电功率在分钟级时间尺度上开展更精细的调控，根据需求响应实时邀约信息和实时电价波动，确定实时需求响应状态，制定调频功率分配策略。

1.3 电力现货市场环境下EV BCSS的调控建模

为描述上述调控流程中的转换关系，反映多时间尺度调控下BCSS充放电计划逐步修正的特性，建立相应的多时间尺度调控模型，如式（1）所示。

调控模型中关于BCSS 运行和电力现货市场规则的关键问题如下。

1）换电供需建模。

EV 用户前往电池配送站换电的时间存在随机性，同时电池配送耗时因交通因素影响也无法精准控制，因此BCSS面对的换电需求存在不确定性。

4）有效需求响应评估。

需求响应收益与需求侧资源的响应情况直接相关，以《广州市虚拟电厂实施细则》为例，其计算公式见附录B式（B7）。

5）电能量申报偏差收益转移。

为防止市场成员利用日前与日内市场的价差不正当套利，设定电能量申报偏差收益转移机制，以《广东现货电能量市场交易实施细则》为例，其计算公式见附录B式（B8）。

2 电力现货市场环境下EV BCSS 的优化调控策略

为确保电力现货市场环境下的BCSS 经济高效运行，本节提出日前-日内-实时多时间尺度的优化调控策略。

2.1 日前阶段

式（14）所示约束条件表示使BCSS 各时段出力低于其最大限额；式（15）所示约束条件表示使所申报调频容量不超过BCSS 的可用容量。此外需遵循1.3节中的关键问题约束。

2.2 日内阶段

日内阶段换电需求、电能量价格存在波动，同时可能收到需求响应日内邀约，因此作进一步优化。基于MPC 构建日内滚动优化调控环节，其优化调控步骤如下［19-20］：

1）将电池荷电状态、换电电量和调频调用电量曲线作为MPC参考曲线用于滚动优化跟踪；

2）建立控制时域和预测时域，考虑到越短的时间间隔内换电需求随机性越强，而越长的时间间隔将导致调控空间缩小，本文以30 min为控制时域，以4 h为预测时域；

4）将控制序列的首个结果u(t)作用于控制对象，并产生输出向量y(t)；

5）至t+1 时段，更新系统状态并将y(t)反馈给滚动优化模型，以校正t时段扰动量r(t)及预测误差。

上述基于MPC 的滚动优化调控步骤中关键环节为滚动预测、滚动优化与反馈校正，其中滚动优化环节建立如下。

选取下网功率Pbuy(t)、换电电量Qev(t)、调频调用预留电量Qf±(t)（Qf±(t)为调频调用预留电量关于时段t的函数）、日内需求响应量Qin，res(t)、各电池充电功率Pbat(t)=[P1(t)，P2(t)，…，Pn(t)]、各电池荷电状态Sbat(t)=[S1(t)，S2(t)，…，Sn(t)]构成状态向量x(t)，如式（16）所示。

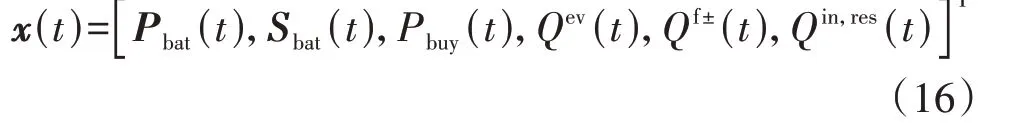
选取换电电量增量ΔQev(t)、调频调用电量增量ΔQf±(t)、日内需求响应增量ΔQin，res(t)、各电池充电增量ΔPbat(t)=[ΔP1(t)，ΔP2(t)，…，ΔPn(t)]构成控制向量u(t)，如式（17）所示。

u(t)=[ΔPbat(t)，ΔQev(t)，ΔQf±(t)，ΔQin，res(t)]T（17）

选取换电需求预测增量Δdev(t)、调频调用预测增量Δdin，f(t)构成扰动向量r(t)，如式（18）所示。

式中：Yr，1为Y1的跟踪参考向量，由日前优化所得；W为偏差权重矩阵，M为价格矩阵，具体如附录B 式（B9）、（B10）所示；m为收益权重系数。目标函数中(Y1-Yr，1)TW(Y1-Yr，1)为跟踪误差的平方和，一定程度上表征全局的经济性；mMY2为调控时段内的运行成本，表征局部经济性。收益权重系数m可调节，以协调全局和局部最优［20］。

2.3 实时阶段

（2）还需遵循式（12）、（13）所示约束条件。

2.4 模型求解策略

上述电力现货市场环境下EV BCSS 的优化调控模型，按照日前-日内-实时的顺序逐步求解。

日前阶段为鲁棒混合整数线性规划问题，本文采用椭球不确定集描述其不确性［21］，并将其等价变换成式（28）—（31）所示的二阶锥规划问题，进而通过商业求解器CPLEX 12.8.0.0 求解，推导过程见附录B式（B11）—（B20）。

日内滚动优化环节为混合整数二次规划问题，实时阶段为混合整数线性规划问题，均使用商业求解器CPLEX 12.8.0.0求解。

3 算例分析

3.1 参数设置

为验证策略有效性，仿真分析图1 所示BCSS，相关参数见附录C 表C1，其中电池参数采用三元锂电池常用装车数据。EV 换电需求基于美国家庭出行调查数据，采用蒙特卡罗方法进行模拟，具体如图2 所示。其中日前以1 h 为时间尺度得到24 个数据点，日内以30 min 为时间尺度得到48 个数据点，并假定EV 中待更换电池荷电状态服从N（0.2，0.042）概率分布。日前、实时购售电电价、调频容量、里程价格预测值根据2019 年美国PJM 市场的运行数据模拟，日前、日内、实时需求响应价格以《广州市虚拟电厂实施细则》为基准设定，具体数据见附录C 图C1、图C2和表C2，预测偏差均设为10%。

图2 不同时段下EV换电需求预测值Fig.2 Forecast values for EV battery demand under different period

3.2 算例分析

3.2.1 优化调控分析

对电力现货市场环境下EV BCSS 的优化调控进行仿真分析，仿真结果附录C图C3—C5。

由仿真结果可见，时段0—3的日前充电曲线和日内充电曲线保持一致，其他时段的日内充电曲线几乎均略低于日前充电曲线。根据2.2节分析，日内调控的目标函数由全局经济性和局部经济性构成，而时段0—5 并无换电需求，完全响应时段2、3 的需求响应邀约符合该调控周期的局部经济性最优目标，同时能够使得用电曲线的跟踪误差最小，即全局收益性最优，因此该时段的日前、日内充电曲线保持一致。在其他时段，日内调控的开展基于更高精度的换电需求预测，则在各时段有更精确的充电电量需求，因此在调控目标中局部经济性的影响下，日内充电曲线相较日前的鲁棒优化曲线有所下降，有效提高了BCSS的运行经济性。

图C3 中BCSS 的3 次长时间对外放电，分别对应3次需求响应：①时段0、1 BCSS 放电，为时段2、3的填谷需求预留充电空间；②时段12、13 同时存在日前和日内两阶段的削峰需求，因此经日前调控后充电功率为负值，进入日内阶段，随着时段0—11的滚动优化，BCSS 中未充分利用的调频电量和换电电量逐渐累积，在该时段日内削峰需求出现时，即可利用该部分能量参与响应；③时段19、20 为日前电价高峰，日前调控下充电功率为负值，进入实时阶段，实时电价再度升高，同时产生填谷需求，因此日内及实时阶段放电功率进一步增大。综上所述，本文构建优化调控策略可有效感知并适应电力现货市场环境。

3.2.2 模型参数的影响

本节重点仿真分析不确定度控制系数ρ和收益权重系数m对整体优化调控的影响。ρ在一定程度上反映了决策者对不确定性所带来风险的回避程度；m反映了决策者对于全局经济性和局部经济性的取舍决策。设置对比模型，仿真分析各模型在典型场景下的策略执行情况，模型参数设置及仿真结果见表1。

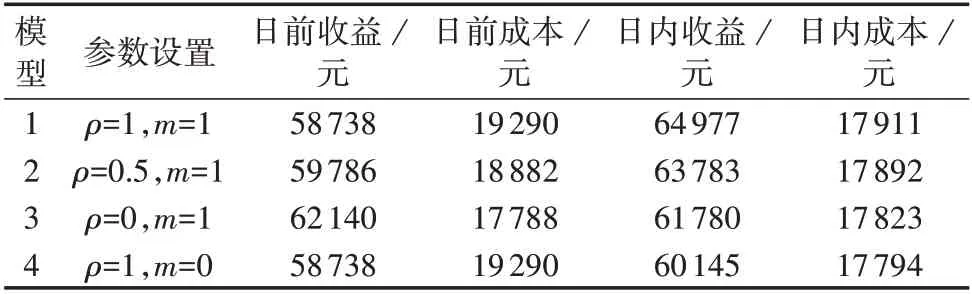
表1 不同参数设置下的调控结果Table 1 Regulation results for different parameters

除模型3 外，其他模型的日前收益均小于日内收益，日前成本均大于日内成本。该差异来自2 个方面：①日前阶段为回避风险将根据ρ在各时段预备足量的电量，从而产生更高的购电成本和电池折旧成本，优化结果相对保守；②日内阶段BCSS 可通过参与日内需求响应获得收益。

模型1—3的日前收益逐步增加，日内收益逐步下降。因为随着ρ降低，日前阶段对不确定性风险的回避程度逐渐减小，策略的保守程度逐渐降低，预期收益逐渐增加；进入日内阶段，模型1 有充足的电量应对换电需求波动并从日内需求响应中获利；模型2 的ρ相对较低，可在一定程度上应对换电需求波动，但难以参与日内削峰需求响应；模型3 在日前阶段未考虑不确定性，完全依靠日内滚动优化应对换电需求波动，在换电高峰时段出现换电收益损失，且未有效参与日内需求响应，因此其日内收益最低且低于日前收益，日内成本大于日前成本。而模型4 的日内阶段仅以跟踪误差最小为目标，在滚动优化过程中仍保持较高保守性，由于剔除了局部经济性目标，模型对需求响应日内邀约无响应，因此其日内收益最低。

3.2.3 需求响应价格与时段的影响

分析需求响应价格与时段对优化调控结果的影响。由1.1节和1.2节可知日前和日内阶段的需求响应有相似的交易机制和参与形式，实时需求响应则对需求侧资源的实时调控能力有更高的要求，因此本节选取日前需求响应和实时需求响应进行分析。

在3.1 节的基础上对日前需求响应价格区间以及实时需求响应时段做出调整，形成如下场景：①场景1，日前需求响应价格、实时需求响应时段均不变；②场景2，日前需求响应价格降低（填谷、削峰价格均降低25%），实时需求响应时段不变；③场景3，日前需求响应价格不变，实时需求响应时段调整（调整为时段17、18）。仿真分析不同场景下策略执行情况，结果见图3、4。

图3 场景1、2的日前优化调控充电曲线Fig.3 Day-ahead optimized regulation charging curves in Scenario 1 and 2

场景1中BCSS在时段2、3响应填谷需求，在时段12、13响应削峰需求；场景2中BCSS未响应时段2、3的填谷需求，对时段12、13 的削峰需求响应量减少，同时时段14、15 的充电功率下降。BCSS 充电伴随电池折旧成本和购电成本，放电伴随售电收益和电池折旧成本，并减少BCSS 内电池电量裕度。BCSS日前优化调控以收益最高为目标，场景1 中BCSS 参与需求响应所获收益大于上述成本支出，且能够保有充足的电量裕度，因此其较大程度地参与需求响应。场景2 中日前需求响应价格区间降低，使得时段2、3 的填谷收益小于对应的成本支出，因此BCSS无响应；而在时段12、13，削峰价格较低，结合时段14、15 的电能量价格数据，BCSS 倾向于降低削峰需求响应量以使整体收益最高。

图4 中场景1 下BCSS 于时段19、20 响应实时阶段的填谷需求，而在场景3 下未响应，因此场景1 的实时曲线较场景3 整体偏低。时段19、20 为日前电价高峰时段，且在实时阶段电价再度上升，同时产生实时削峰需求。BCSS 后续换电需求较小，在确保调频容量的基础上有充裕的放电空间进行响应；时段17、18 为换电需求高峰期，此时BCSS 需大量充电，同时满足日前承诺的调频容量，因此虽然该时段的实时需求响应收益较高，但BCSS 无响应。由此可见，BCSS 虽然能够满足实时需求响应的快速响应要求，但受到换电服务的限制，同时与调频辅助服务参与程度相互制约，其灵活可调性有所下降。