基于需求响应潜力模糊评估的电动汽车实时调控优化模型

2022-10-15周星月黄向敏张勇军姚蓝霓杨景旭

电力自动化设备 2022年10期

周星月，黄向敏，张勇军，唐渊，姚蓝霓，杨景旭

（1. 华南理工大学电力学院，广东广州 510640；2. 南方电网数字电网研究院有限公司，广东广州 510670）

0 引言

随着“双碳”战略目标的提出，电动汽车EV（Electric Vehicle）因其良好的环保特性和负荷可调控特性在节能减排和需求响应DR（Demand Response）方面显示出较大优势，倍受关注。EV 实时调控可以视作一种灵活的实时DR 资源［1］，是解决EV 大规模接入造成配电馈线重过载等问题的重要手段。

目前关于EV 参与DR 的研究大多集中在价格型DR［2］上，文献［3-4］分别以削峰填谷和EV 充电成本最小为目标提出了基于分时电价的EV 有序充电模型。但价格型DR 对EV 充电活动的引导作用有限，有必要结合激励型DR 优化EV 的充放电行为。激励型DR 一般以合同形式约定了用户权利和义务，往往以实施方的角度进行直接负荷控制［5］，旨在满足实施方需求。在目前的激励型DR 研究中，对于EV 响应潜力的计算通常只考虑了激励电价的影响，如文献［6］以双曲正切函数确定不同激励下的EV响应量，文献［7］类比价格型DR弹性系数引入激励型DR 弹性系数，描述激励价格变化给用户响应潜力带来的影响。文献［8-9］考虑到响应量的波动性，基于消费者心理学模型建立了用户响应量及其波动程度和激励水平的关系模型。但用户在不同时段表现出的响应意愿和当前时刻的电价、EV 电量需求和剩余驻留时间等多种因素密切相关，仅考虑激励水平的影响无法建立准确的潜力评估模型，EV 聚合商EVA（EV Aggregator）的收益和配电网的削峰效果都会因此大打折扣。此外，目前的实时调控研究还没有充分挖掘EV 的车网互动V2G（Vehicle to Grid）［10］响应潜力，因此如何综合客观响应能力约束和主观响应意愿评估用户的充放电响应潜力，对于充分挖掘EV 调控潜力以及提高调控准确性具有重要意义。

现有关于EV 的DR 策略多聚焦于日前时间尺度［11-12］上的研究，如文献［9］提出一种双重激励机制引导EV参与日前DR，提高了EV备用服务能力。但随着快充需求的增长，快充场所的EV到达和离开时间及初始电量具有较大的随机性［5］，日前DR 策略难以取得较好的实用效果，而EV 的实时DR 可以根据实时更新的负荷数据及时调整策略，具有更大的工程价值，因此有必要对EV 的实时DR 进行研究。基于此，文献［13］提出了一种基于EV迟滞控制模型的实时DR 策略，注重于电网侧功率的消纳；文献［14］考虑用户侧的利益，建立了计及激励型主动DR 的EVA 在实时电力市场的最优充电调度模型；文献［15］根据路况、距离等因素设计了行驶中EV的激励电价两步制定方法，考虑了EVA 的激励成本，但不适用于对已经达到充电站的EV 进行调控。较少有快充站内的实时DR 策略能根据用户不同响应潜力制定激励电价，难以充分调动用户的积极性，也缺乏对EVA 侧利益的考虑，影响到DR 实施效果。因此如何根据不同用户响应能力和响应意愿的差异制定合理的激励电价，并通过EVA 激励电价和用户充电计划两层决策优化来提高EV参与响应的主动性，对改善EV实时调控的实际应用效果具有重要意义。

基于此，本文提出了一种基于DR 潜力模糊评估的EV实时调控优化模型。首先，建立用户的客观响应能力约束模型和考虑激励水平的主观响应意愿评估模型，结合客观响应能力和主观响应意愿计算EV响应潜力。然后建立激励型实时DR双层优化模型，上层模型以EVA 激励成本最小为目标优化EVA激励电价，下层模型以用户平均充电满意度最高为目标优化EV充放电功率。最后，通过仿真验证本文所提模型和方法的有效性。

1 激励型实时DR框架

本文所提激励型实时DR 框架为“电网公司-EVA-用户”，如图1 所示。EVA 作为电网公司与用户的中介，可实现EV 的分布式管理与调度，是本文所提激励型实时DR 的主体。本文假设充电桩具备独立的信息处理与计算的能力，可以实现与EVA 的通信及对EV 充电功率的调控。在激励型实时DR中，充电站以与用户签订协议的方式规定其参与响应的义务，存在调控需求时EVA 可以直接对签约用户的EV 充电功率进行控制。EVA 通过为配电网提供DR 服务和为EV 提供充电服务获得收益［16］，并向参与DR的用户支付一定的经济激励。

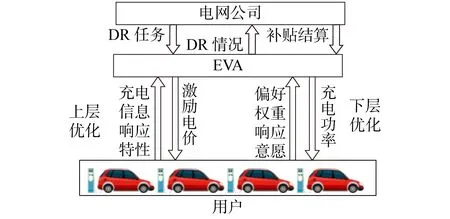
图1 实时DR框架Fig.1 Framework of real-time DR

实时调控的优化流程图见附录A 图A1，具体步骤如下：①步骤1，以每5 min 为1 个时段，每个时段配电网调度中心根据当前负荷和峰荷控制目标确定下一个时段是否存在调控需求，若存在则确定DR任务并公布给EVA；②步骤2，智能充电桩在EV 进站时获取其初始电量、期望电量、预计离开时间等信息，根据EV 充电需求等约束计算其响应功率边界，确定其客观响应能力；③步骤3，建立考虑激励水平的用户响应率模型，在此基础上采用模糊推理确定不同电价、电量需求和剩余驻留时间下的用户主观响应意愿；④步骤4，结合EV 的客观响应能力和主观响应意愿计算其响应潜力，据此制定合理的激励电价以最小化EVA 激励成本，并将激励电价向用户公布；⑤步骤5，对于接受激励电价的用户，根据其进站时提供的时间-费用偏好权重建立充电满意度模型，以EV平均充电满意度最大为目标优化其下一个时段充放电功率，并由智能充电桩进行相应调控。

2 考虑主客观因素的EV响应潜力

EV 响应潜力受到多种因素的影响，为建立准确的DR 潜力评估模型，本文在EV 充放电模型的基础上建立EV 的客观响应能力约束模型，提出考虑电价、电量需求等因素的用户主观响应意愿评估模型，基于模糊推理确定用户的充放电响应潜力。

2.1 EV充放电模型

以锂电池为对象，在建模过程中忽略电池自放电过程，并近似认为每个优化时段内充放电功率恒定，可得到单辆EV的充放电模型，如式（1）所示。

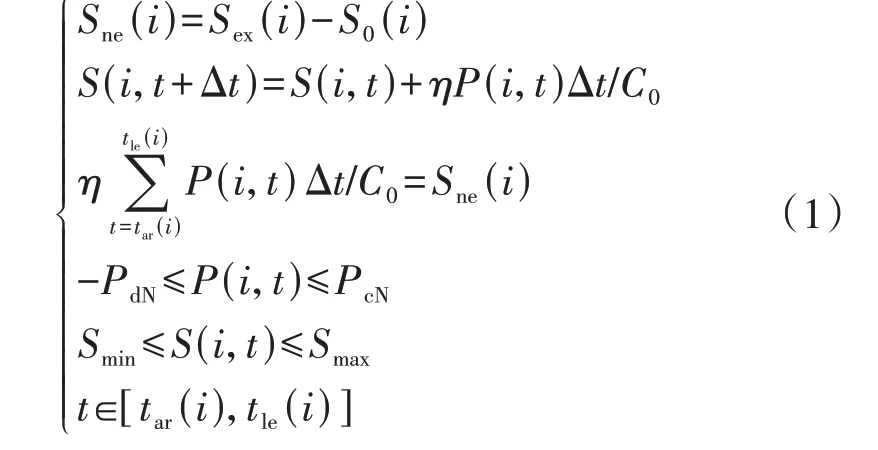
式中：Sne(i)为用户i的充电电量需求；C0为电池容量；Sex(i)为用户i的期望荷电状态（SOC）；S0(i)为用户i接入时的SOC；S(i，t)为用户i在t时刻的SOC；η为充（放）电效率，当EV 充电时η取充电效率ηc，当EV放电时η取放电效率ηd的倒数；P(i，t)为用户i在t时刻的充（放）电功率；Δt为时段间隔；PcN、PdN分别为EV 的额定充、放电功率；Smax、Smin分别为EV 电池的SOC上、下限；tar(i)、tle(i)分别为用户i的到站时刻和预计离开时刻。

2.2 EV的客观响应能力约束模型

EV 客观响应能力是指满足其充电需求下的最大响应功率，受到EV 电池安全电量、EV 充电需求、充电桩额定功率的限制，呈现时变特征，可以通过EV的充放电功率边界计算。各类约束如下。

1）EV电池安全电量约束。

为了保证EV电池寿命，EV参与DR带来的电量变化需要满足电池的安全电量约束，即：

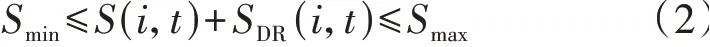
式中：SDR(i，t)为用户i在t时刻以响应功率P(i，t)充（放）电时造成的SOC变化量，计算式见附录B式（B1）。

2）EV充电需求约束。

为了满足用户出行需要，EV 需要在离站之前充电至期望电量，因此其参与DR 带来的电量变化量SDR(i，t)需要满足：

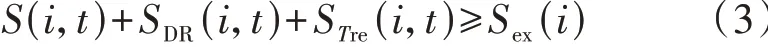
式中：STre(i，t)为t时刻用户i在剩余驻留时间Tre(i，t)内保持额定充电功率充电时的SOC变化量，STre(i，t)、Tre(i，t)的计算式分别见附录B式（B2）、（B3）。

3）充电桩额定功率约束。

EV 响应功率受到充电桩额定功率的限制，接受V2G的用户和不接受V2G的用户响应功率需要分别满足式（4）、（5）所示约束条件。

2.3 用户的主观响应意愿评估模型

对于用户而言，是否参与DR 由用户主观意愿决定，故EV 响应潜力不仅受其客观能力的限制，还需考虑用户主观意愿的影响。以响应率表示用户的主观意愿，即用户愿意响应的最大功率占客观响应能力的比例，建立考虑多种因素的主观意愿评估模型。

2.3.1 考虑激励水平的用户响应率模型

根据消费者心理学模型［17］，当激励电价不超过用户的临界激励时，用户不愿意进行响应；当激励电价超过临界激励时，用户开始响应，且愿意响应的程度随激励电价的提高而增大，直到达到最大响应程度。但用户在同一激励水平下的响应意愿并非固定不变，会受到其他因素的影响，具有波动性，因此需要考虑响应意愿的波动程度。为此，对同一激励水平下的用户意愿设置积极响应和消极响应2 种情况，以两者响应率之差表示用户响应意愿的波动程度。同时，考虑到用户在同一激励下对充、放电响应的接受程度不同，本文设置用户的充放电差异化响应率模型如图2所示。图中：c为EVA 对用户单位响应电量的激励价格；fc、fd分别为用户的充、放电响应率；fcm、fdm分别为用户最大充、放电响应率；cc1为用户充电响应临界激励，当激励电价高于该值时，用户充电响应率总是大于0；cd1为用户放电响应临界激励，当激励电价高于该值时，用户放电响应率始终大于0；ccm为充电响应饱和激励，当激励电价高于ccm时，用户充电响应率总保持fcm；cdm为用户放电响应饱和激励，当激励电价高于该值时，用户放电响应率总保持为fdm；cd0为使用户参与放电响应的最低激励水平；曲线fopc(c)、fpec(c)分别为用户充电积极响应和充电消极响应曲线，对应表达式分别见式（10）、（11）；曲线fopd(c)、fped(c) 分别为用户的放电积极响应和放电消极响应曲线，对应表达式分别见附录B式（B5）、（B6）。

图2 EV用户的充放电响应率模型Fig.2 Charge-discharge response rate model of EV user

2.3.2 用户积极响应偏向程度

从上述模型可知，在某一激励水平c下，用户响应率波动范围为[fpe(c)，fop(c)]。当激励水平较低时，用户响应率波动范围较大。考虑到用户主观响应意愿除了和激励水平相关，还受到充电电价、EV 电量等其他因素的影响，在上述模型基础上定义积极响应偏向程度τ，以描述用户受其他因素影响而偏向积极响应的程度，以此确定用户实际响应率，即：

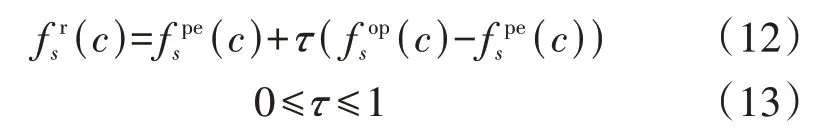
式中：frs(c)为用户的实际响应率，下标s表示EV 响应方式，当EV 通过充电参与DR 时s取c，当EV 通过放电参与DR时s取d。

2.4 基于模糊推理的EV响应潜力评估模型

2.4.1 积极响应偏向程度的模糊推理

不同用户的积极响应偏向程度τ有所差异，受到多种因素的影响。本文主要考虑当前充电电价p、EV当前电量需求Sn和EV剩余驻留时间Tre这3个因素对τ的影响。当前时段的充电电价低时，用户偏向积极响应，τ偏高，反之τ偏低；当前电量需求大时用户偏向消极响应，τ偏低，反之τ偏高；当剩余驻留时间长时用户偏向积极响应，τ偏高，反之τ偏低。由于难以建立四者之间准确的解析模型，而模糊控制可以在不清楚被控对象内部结构的情况下通过人为经验建立模型，受文献［18］的启发，本文采用模糊推理确定不同p、Sn、Tre下的τ。

考虑到用户当前电量需求Sn以SOC 来表示，取值范围为［0，1］，故将p和Tre进行归一化处理后再作为模糊推理的输入，如式（14）、（15）所示。

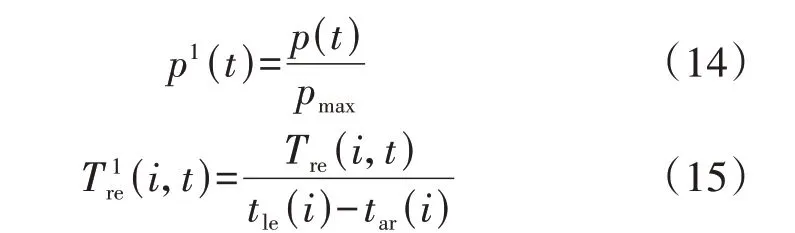
式中：p1(t)为t时刻充电电价p(t)的归一化值；pmax为EVA 峰时段的充电电价；T1re(i，t)为用户i在t时刻剩余驻留时长Tre(i，t)的归一化值。

通过模糊推理确定用户i在t时刻的积极响应偏向程度，即：

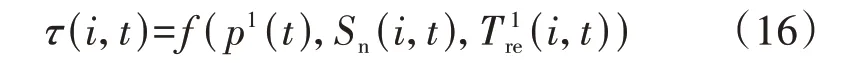
式中：Sn(i，t)为用户i在t时刻的电量需求。式（16）表示用户i在t时刻积极响应偏向程度τ(i，t)由模糊逻辑控制器f(·)运算输出，各变量的模糊化语言见附录B表B1，模糊规则见附录B表B2。

2.4.2 EV充放电响应潜力计算方法

结合用户客观响应能力和主观响应意愿计算EV充放电响应潜力，如式（17）—（19）所示。

3 激励型实时DR的双层优化模型

在获取用户的响应潜力后，为给用户提供是否参与DR 的选择权，同时兼顾各方利益，采用双层优化模型确定EVA 激励电价和用户响应功率。上层优化变量为EVA 对用户的激励电价，完成优化后将结果传递到下层作为下层的输入参数，在下层进行EV充电功率的优化。

3.1 上层优化——激励电价优化模型

3.1.1 激励电价的优化目标

激励型实时DR 的上层优化为EVA 激励电价的优化。在DR 过程中，激励电价的调整范围和调整方式在合约中已经规定，是公开透明的。因此本文默认与充电站签约的用户都是接受充电站的激励电价及其调整机制的。由第2节可知，对于τ较高的用户，使其达到某一响应率所需要的激励电价相对于τ较低的用户更低。当τ较高的用户的客观响应能力较大时，EVA 可以通过较低的激励成本获取较大的响应潜力。因此，本文根据考虑主客观因素的用户响应潜力制定合理的激励电价，尽量降低EVA 激励成本，提高EVA 的收益（EVA 收益的计算方法如附录C式（C1）—（C8）所示），即：

式中：c0、cm分别为EVA 制定的最低、最高激励电价；δr为满足配电网当前时刻削峰需求Pne(t)而设定的总响应潜力裕度。

3.2 下层优化——EV充放电功率优化模型

3.2.1 充放电功率的优化目标

在确定激励电价后，EVA将其下发给各用户，引导用户申报最终的响应意愿。响应的功率越大，用户获得的收益越高，但充满电所需要的时间会因此增加。考虑到不同用户对充电时间和充电费用具有不同的偏好，且两者无法同时降低，本文提出包含时间和费用2 个方面的用户充电满意度模型，并以平均充电满意度最高为准则优化各EV充（放）电功率。

式中：Trc(i，t)、T′rc(i，t)分别为t时刻用户i参与DR前、后的后续充电时长；F(i，t)、F′(i，t)分别为此时刻用户i参与DR 前、后的后续充电费用，计算方法如附录C式（C9）—（C19）所示。

3.2.2 充放电功率的优化约束

为满足用户的充电需求，EV 充（放）电功率需要处于该时段的响应功率边界内，同时需要使EV的总响应潜力需要满足电网削峰需求，因此EV充（放）电功率的优化约束如下：

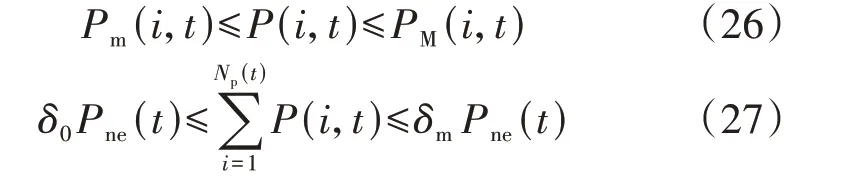
式中：δm、δ0分别为避免欠响应和过响应设置的总响应功率上、下裕度。

3.3 双层优化模型的求解算法

本文假设用户激励电价可以由EVA 实现连续调节，EV 充放电功率可以由智能充电桩实现连续调控，因此式（20）、（23）均为连续非线性求解问题，双层优化均采用粒子群优化算法求解［19］。

在本文所提双层优化策略中，激励电价和充（放）电功率分别为上、下层优化模型的变量，即需要寻优的粒子，粒子维度为参与DR 的EV 数量，上、下层优化中的粒子位置范围分别根据EVA 激励电价的上下限和各EV的充电功率边界设置，同时还需要满足相应模型的优化约束，粒子适应度为优化模型中的目标函数值。迭代过程中，每个粒子根据自己当前适应度与个体历史最优适应度和群体历史最优适应度更新自己的位置，直到满足迭代停止条件后停止搜索，获取最优解。在获得最优激励电价后，将其作为下层优化模型的参数，进而求解EV充（放）电功率，实现EV参与DR的实时调控。

4 算例分析

4.1 仿真参数设置

本文以商业区常规负荷作为基础负荷，并考虑EV 接入配电网后对负荷峰值的影响。峰荷控制目标为5 266 kW；EV 充电的峰谷平时段划分采用广州市某充电站的实际电价数据，如附录D表D1所示。

在4.2 GHz 处理器和16 GB 内存的计算机上进行仿真，仿真参数设置如下：EV 总数为600 辆；PcN、PdN均为60 kW；C0为40 kW·h；ηc、ηd均为0.9；Δt为5 min；S0服从N（0.15，0.1）的正态分布；Sex服从U（0.6，0.9）的均匀分布；cc1、ccm分别为1.5、3.5 元／（kW·h）；cd0、cd1、cdm分别为0.5、2.0、4.0 元／（kW·h）；fcm、fdm均为1 p.u.；c0取0；cm为4.5元／（kW·h）［15］；参与响应的补贴标准bEVA为1.5 元／（kW·h）［16］；αT、αF均为0.5；γT、γF根据MT、MF的数值大小分别取为2.5和1；单位放电量的电池损耗折算成本L为0.5元／（kW·h）［20］；δ0、δm分别为0.9、1.1；假设各响应时段签约用户均接受调控，即Nc和Np相等；附录A 图A1 中上、下层优化粒子群数m0和m1均为1000，迭代次数Im0和Im1均为300。

4.2 基于双层优化的实时DR策略有效性分析

假设签约EV 用户占比为100%，采用本文所提方法对各响应时段的EV 激励电价和充电功率进行优化。整体EV 负荷优化曲线如图3 所示，各参与方相关响应指标如表1 所示，某响应时段参与响应的EV 的削减功率如附录D 图D1 所示，第188 辆EV 调控前、后的充电曲线如附录D图D2所示。

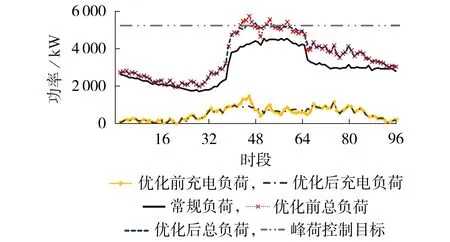
图3 EV负荷优化情况Fig.3 EV load optimization conditions

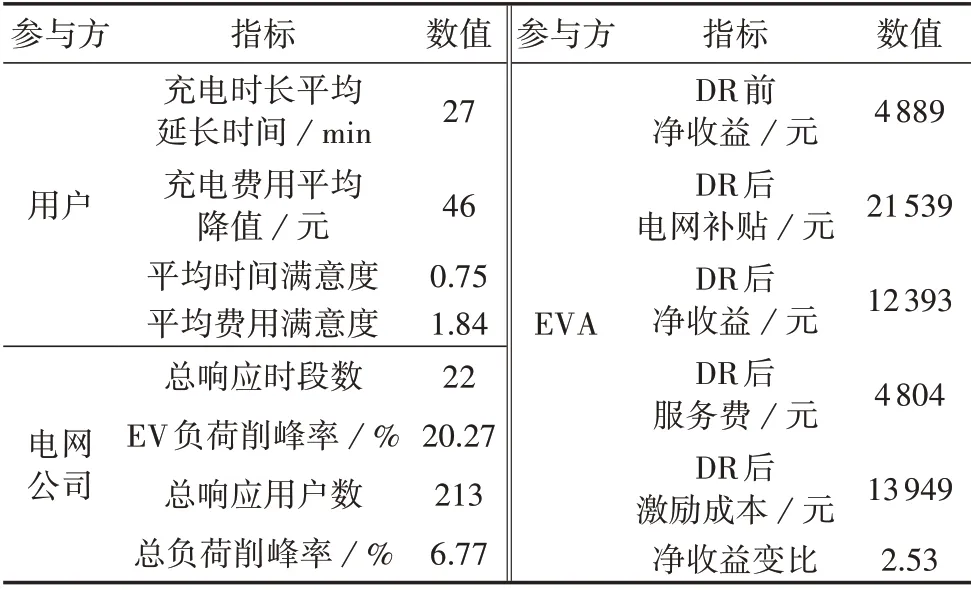
表1 DR各参与方的响应指标Table 1 Response indicators of DR participants

由图3 和表1 可知，由于在实施DR 过程中充分考虑了用户的客观响应能力和主观响应意愿，充电负荷响应效果良好。当总负荷即将超过峰荷控制目标时，电网公司向EVA发布DR任务，共有22个时段实施了DR，充电负荷削峰率达20.27%，总负荷削峰率达6.77%，配电网峰荷得到较为明显的改善。EVA参与DR后净收益达到12393元，净收益变比达到2.53，收益有明显提升。参与DR的用户的充电时长平均延长27 min，平均时间满意度达0.75，充电费用平均降低了46 元，平均费用满意度达1.84，即用户通过延长充电时间降低了充电成本。各方利益均得到满足，激励型实时DR策略的有效性得到验证。

由附录D 图D1 可知，在响应时段EVA 对EV 充电功率的分配与其激励电价的大小相关。由于EVA对用户的激励电价越高，用户响应单位功率能获得的收益越大，其费用满意度就越高，因此激励电价高（激励电价的优化分析如4.3.1 节所示）的用户削减功率大。由附录D 图D2可知，单辆车的充电活动在调控后由存在调度需求的时段转移到后续非响应时段，同时，为了满足用户的充电目标，EVA 会尽可能安排用户在最近的非响应时段充电。

此外，本文仿真完成单个时段的实时调度优化只需要2.5 s，可以满足实时调度的计算需求。

4.3 激励电价和充放电功率优化方法的有效性分析

4.3.1 考虑响应潜力的激励电价优化方法有效性分析

为了验证本文根据用户响应潜力制定激励电价这一方法的有效性，与文献［8-9］中只考虑激励电价对响应潜力的影响从而制定电价的方法进行对比。假设签约用户占比为100%，只考虑激励电价对响应潜力的影响时积极响应偏向程度τ为固定值，将τ分别设置为0.1（情景a）和0.9（情景b），与本文方法（情景c）进行对比，不同情景下的相关指标见表2，总负荷和充电负荷的优化情况分别见附录D图D3、D4。

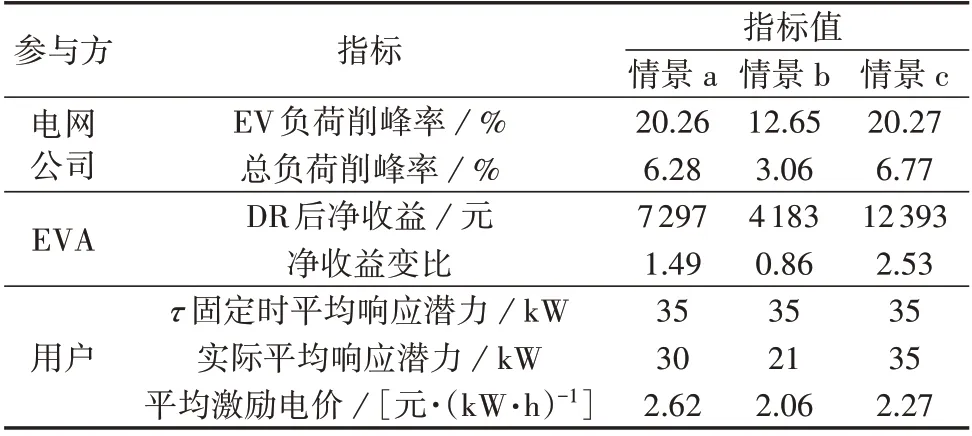
表2 不同情景下DR各参与方的响应指标Table 2 Response indicators of DR participants in different scenarios

由表2 和图D3、D4 可知：与情景c 相比，情景a下EVA 的净收益偏低，用户的平均激励电价较高，这是因为当τ较低时需要较高的激励电价才能使用户提供足够的响应潜力，此时用户的响应潜力因为激励电价提高而增大，能够满足削峰需求，但此时EVA 需要付出比情景c 更大的激励成本，其收益降低；情景b 下的配电网的削峰率和EVA 的净收益最低，用户的平均激励电价也最低，这是由于该情景下设置的τ值较高，只需要以较低的激励电价就能使用户提供较大的响应潜力，但实际上用户获得的激励电价降低，其响应潜力因此减少，负荷的削峰率降低，出现了响应不足的情况，电网公司减少对EVA的补偿，EVA的净收益随之降低。

故仅考虑激励电价对用户响应潜力的影响时，EVA无法根据用户实际响应意愿制定合理的激励电价，会出现EVA 收益减少及削峰效果差的问题，而本文方法考虑多种因素对用户响应潜力的影响，制定的激励电价更合理，能更好地满足各方需求。

4.3.2 考虑不同偏好权重的充放电功率优化方法有效性分析

为了验证本文充放电功率优化方法有效性，假设签约用户占比为100%，对比分析用户不同的时间-费用偏好权重下的响应指标，如表3所示。

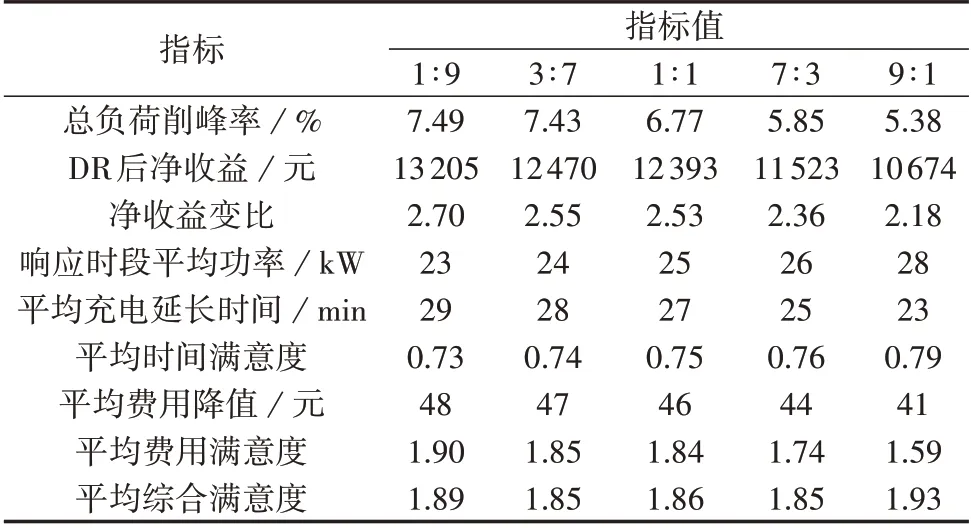
表3 用户不同偏好权重下的响应情况Table 3 Response conditions of users with different preference weights

由表3 可知，当用户对时间和费用的偏好权重不同时，用户的平均综合满意度较为一致，但总负荷削峰率、EVA 收益变比和用户不同方面的充电满意度相差较大。当用户的费用偏好权重设置较高时，用户的平均充电费用降值相对较大，费用满意度较高。因为此时用户参与DR 时更偏向于充电费用的降低，希望通过削减更多的充电功率获得更大的激励补偿，总负荷的削减程度因此增加，负荷削峰率相对于其他情况更高，电网公司对EVA 的补贴增加，故EVA 收益相对于其他情况更高，此时用户平均充电时间因为充电功率小而延长较多，故时间满意度低于其他情况。总体而言，用户可通过设置不同的时间-费用偏好权重使其不同偏好需求得到满足，综合满意度也可以保持较高的水平，验证了本文所提考虑用户不同偏好优化充放电功率方法的有效性。

4.4 不同的用户V2G参与度的响应情况分析

为验证本文考虑EV的V2G模式的优越性，分析不同的用户V2G 参与度下的优化结果，如表4所示，某用户接受V2G与否的响应指标见附录D表D2。

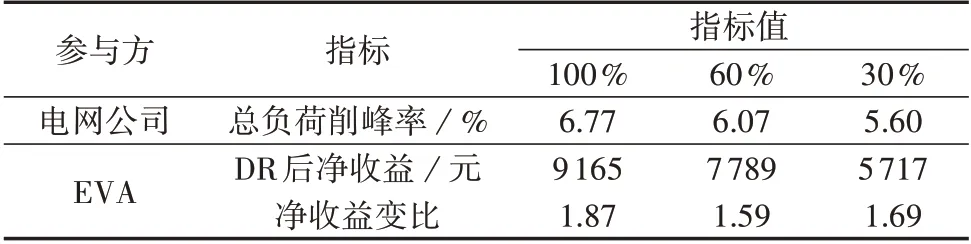
表4 不同的用户V2G参与度下的优化结果Table 4 Optimal results with different users V2G participation

由表4 可知，当V2G 的参与度下降时，总负荷削峰率和EVA 的收益随之降低。这是因为当参与V2G 的用户减少时，EV 的总客观响应潜力下降，EVA 为满足配电网的削峰需求，需要提供给用户更高的激励电价以提升用户响应率，从而对EV的充电功率进行更大幅度的削减，这导致EVA 激励成本增加，其净收益和收益变比因此降低。由表D2 可知，该用户参与V2G 时，充电时间与不参与V2G 时相比有所延长，这是因为当用户参与V2G 时，响应时段充电功率更低，花费的充电时间更多，时间满意度有所降低。但用户参与V2G 时充电费用明显下降更多，这是因为用户允许放电时能提供更多的响应潜力，且EVA 对用户参与放电响应的单位激励电价高于充电响应，因此用户接受V2G 时能够获得更多的收益，其费用满意度和综合满意度更高。

根据上述分析，考虑EV 的V2G 模式能够实现更好的削峰效果，提升EVA 的收益，用户接受V2G也能获得更多收益，提高充电满意度，故有必要考虑V2G模式，提升DR的实施效果，实现多方共赢。