发动机喷流对火箭气动特性影响

任一鹏， 郑 晨， 闵昌万

(1. 北京宇航系统工程研究所， 北京 100076; 2. 中国运载火箭技术研究院， 北京 100076)

引 言

火箭在有动力飞行过程中， 发动机喷流与自由来流的相互作用会形成复杂的喷流诱导流动分离-再附现象和底部喷流抽吸现象[1-2]， 使得箭体附近的流场与无喷流状态差异明显。 有、 无喷流时的流场差异， 对火箭表面压力分布及整体气动力/力矩特性都会产生较为明显的影响。

气动特性设计的首要任务是获取火箭在飞行状态下真实准确的气动力/力矩系数[3-4]， 但受限于国内常用风洞的尺寸规模和火箭试验模型的尾部支撑方式， 对于长细比较大(如大于12)的火箭， 风洞测力试验中通常难以考虑发动机喷管及喷流的影响。 对于专门研究喷流影响的风洞试验， 模型通常采用腹部/背部支撑方式， 仅可观测喷流与自由来流相互影响下的复杂流场结构， 但由于支撑方式对飞行器试验模型的干扰显著， 因此在研究喷流影响的试验中较难同时获取飞行器在喷流影响下的准确气动力和气动力矩特性。

某次火箭飞行过程中超声速段的气动辨识结果与依据无喷流状态风洞测力试验结果的比较如图1所示， 由图可见， 对于火箭超声速飞行段的法向力系数CN， 发动机工作时间段和关机时间段的辨识结果与设计结果均较为吻合， 但是对于火箭超声速段的轴向力系数CA， 发动机关机时间段的辨识结果与设计结果较为接近， 而发动机工作时间段的辨识结果明显小于设计结果， 尽管发动机工作时间段的轴向力系数在设计过程中已经按照常规方法扣除了底部压力的影响。

(a) Normal force coefficient， CN

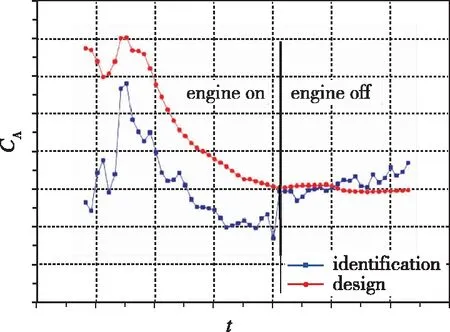
(b) Axial force coefficient， CA图1 某火箭超声速段气动辨识结果与设计结果比较Fig. 1 Comparison between aerodynamic identification results and design results of a rocket supersonic flight

由上述气动辨识结果与设计结果的比较可见， 发动机喷流对火箭气动特性的影响是显著的， 在气动设计过程中有必要详细考虑喷流影响。

对于喷流影响， 近年来开展了相关喷流风洞试验研究[5-9]， 在分析喷流干扰流场结构的基础上， 还尝试分析试验状态下底部喷流对飞行器气动力/力矩特性的影响， 但喷流测力试验状态与飞行状态存在差异(模型尾部支撑装置对喷流的干扰影响、 试验喷流压力比和温度与真实飞行状态的差异等)、 试验设备复杂(如喷流发生装置、 天平隔离装置等)、 试验效率低、 试验费用高等不足之处， 导致试验结果难以在飞行器工程设计研制过程中直接使用。 CFD仿真方面， 较多研究集中在侧向或底部喷流与自由来流的干扰流场结构分析方面[10-16]， 较少研究飞行器工程设计研制过程中最直接的关注点——喷流对飞行器气动力/力矩影响的系统性研究。

随着飞行器精细化设计的发展， 发动机喷管/喷流对飞行器气动特性和姿态控制品质的影响日益被重视[17-18]。 本文采用CFD方法， 对比分析了亚声速和超声速典型状态下有、 无底部喷流影响时的火箭气动特性差异， 从气动力/力矩系数、 压力分布、 流场结构不同层次分析发动机喷流对火箭气动特性的影响， 为火箭气动特性设计提供参考。

1 气动外形

火箭气动外形如图2所示， 包括箭体和尾舵， 其中箭体为轴对称外形， 尾部有4片“+”形布局的梯形全动空气舵。 火箭长细比约13.3， 发动机喷管扩张比约7.6。

图2 火箭气动外形Fig. 2 Aerodynamic configuration of the rocket

2 数值计算方法及网格

2.1 数值方法

本文选用基于格点格式的三维可压缩Reynolds平均N-S方程有限体积求解器。 对流项的空间离散采用2阶精度的TVD格式， 选用Minmod通量限制器; 黏性项的空间离散采用2阶精度的中心差分格式; 时间推进采用隐式LU-SGS格式。 湍流模式选用k-ε的两方程模式。

本文CFD仿真考虑两组分气体， 来流为空气， 喷流为另一种有别于空气的等效高温高压气体介质， 其总温、 总压、 比热比等物理属性根据发动机地面试车测量数据等效确定。 仿真过程中忽略空气和喷流之间的化学反应， 即为双组分化学反应冻结流计算。

2.2 计算网格及边界条件

选择能够同时适应亚声速和超声速计算的柱形计算域， 如图3所示， 入口边界到火箭头部的距离为10L， 出口边界到火箭尾部的距离为30L， 四周边界到火箭外壁面的距离为20L， 其中L为火箭长度。

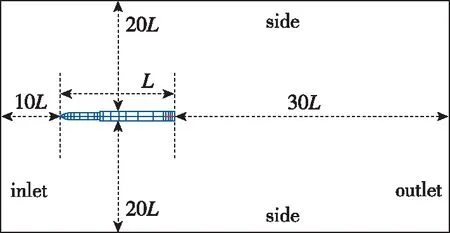
图3 计算域示意图Fig. 3 Schematic diagram of computational domain

计算采用O-H型多块结构化网格， 喷管及尾舵附近做局部拓扑优化调整和网格适应性加密， 火箭附近的附面层网格高度从第1层的1.0×10-6m等比增大至第40层的1.3×10-3m。 无喷流状态时， 发动机喷管在喉部位置处封闭， 计算网格从发动机喉部位置开始; 有喷流状态时， 发动机喷管喉部打开， 计算网格从发动机燃烧室位置开始。 网格总数8×106～8.5×106， 如图4所示。

图4 计算网格Fig. 4 Computational mesh

边界条件设置中， 入口和四周边界为远场压力边界， 按照10 km大气环境， 给定静压为26 450 Pa, 静温为223.3 K，Ma分别为0.7和2.0; 出口边界在Ma=0.7时为零梯度出口边界， 在Ma=2.0 时为超声速出口边界; 火箭壁面为无滑移固壁边界; 无喷流状态时， 发动机喉部同样为无滑移固壁边界; 有喷流状态时， 发动机燃烧室底部为总温总压入口边界， 给定燃烧室总温为3 600 K， 总压为8 MPa， 即有喷流状态时的发动机燃烧室压力与外界环境压力之比约为302.5。

Ma分别为0.7和2.0时， 基于火箭长度的Reynolds数分别约为7.9×107和2.3×108， 均属于强湍流Reynolds数范围。

2.3 准确性验证

2.3.1 无喷流状态验证

按照2.1节中的数值方法和网格拓扑结构及尺寸， 开展某火箭(外形为轴对称箭体+尾舵)在亚声速(Ma=0.8)和超声速(Ma=2)状态下的气动特性CFD计算， 火箭轴向力系数CA、 法向力系数CN、 相对质心俯仰力矩系数Cmzg的计算结果与试验结果的比较如图5所示， 箭体轴向横截面和尾舵展向截面上压力系数Cp的计算结果与试验结果的比较如图6所示。 由图可见， CFD计算获得的火箭气动力/力矩系数与试验结果的规律及具体量值都吻合较好，CA,CN,Cmzg的相对偏差分别小于10%, 5%, 8%， 满足气动设计的精度要求; CFD计算获得的箭体锥段和尾舵表面的压力系数与试验结果的分布规律及具体量值都吻合较好， 能够捕捉到箭体背风面的流动分离-再附及尾舵表面的流动压缩-膨胀特性(见图7, 8)。

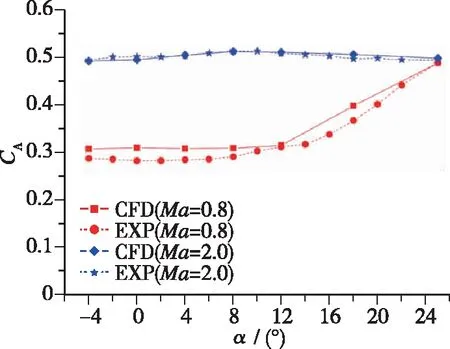
(a) Axial force coefficient， CA

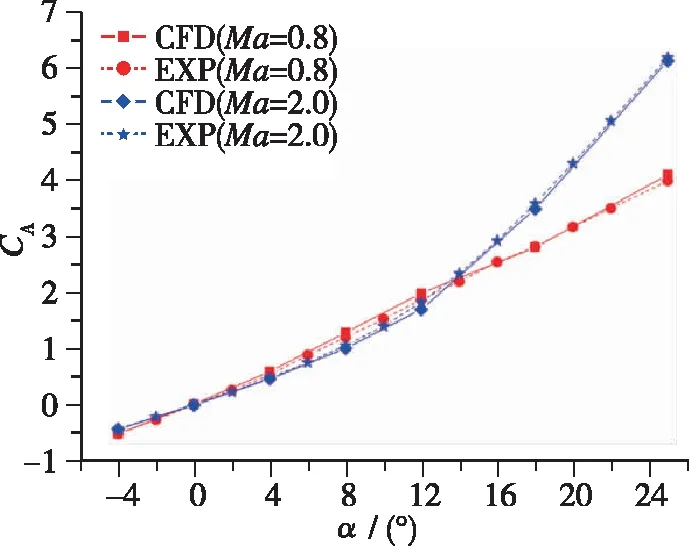
(b) Normal force coefficient， CN

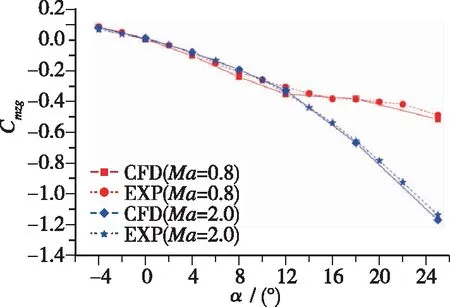
(c) Pitching moment coefficient relative to centroid， Cmzg图5 某火箭气动力/力矩系数CFD与试验结果比较Fig. 5 Comparison of aerodynamic coefficient between CFD and experiment for a rocket

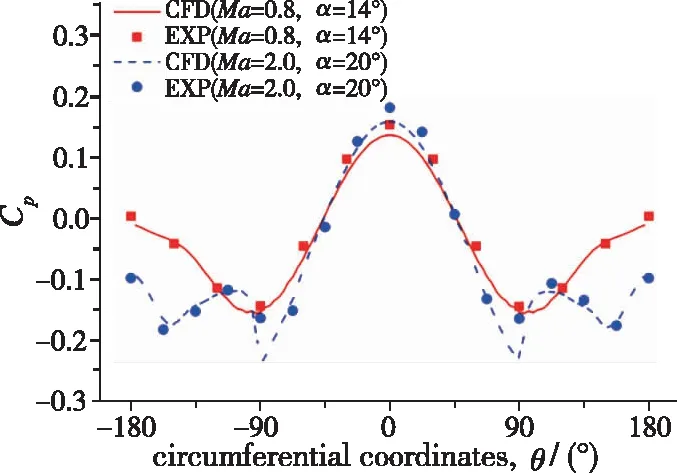
(a) Cross section of rocket cone body

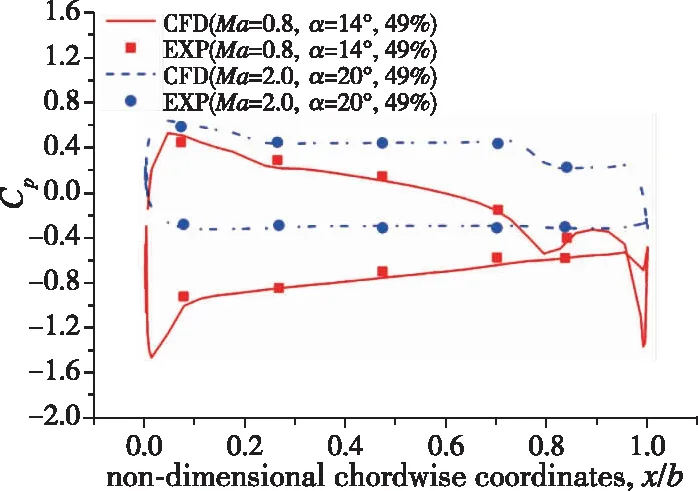
(b) Spanwise section of rudder图6 某火箭压力系数分布CFD与试验结果比较Fig. 6 Comparison of pressure coefficient between CFD and experiment for a rocket

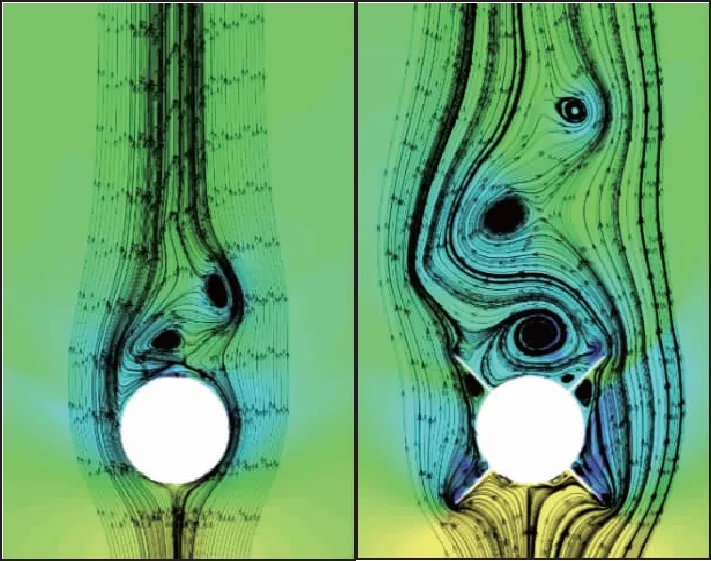
图7 箭体背风面不同轴向位置流场(Ma=0.8， α=20°)Fig. 7 Flow field structures at different axial positions on the leeward side of rocket(Ma=0.8, α=20°)

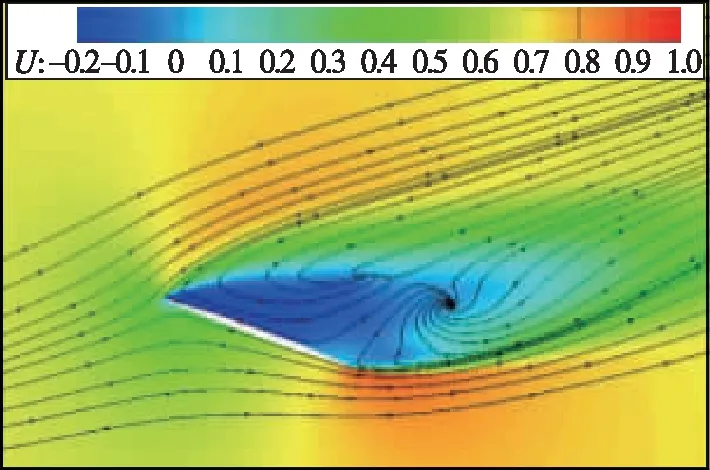
(a) Ma=0.8, α=20°

(b) Ma=2.0, α=20°图8 尾舵背风面流场结构Fig. 8 Flow field structures of leeward side of tail rudder

2.3.2 有喷流状态验证

文献[8]介绍了轴对称箭体横向喷流影响试验结果， 按照此试验状态开展相应的CFD验证。 模型如图9所示， 为长细比2的Φ50 mm轴对称箭体，Φ5 mm的圆形侧向喷口位于箭体约中段位置， 喷流气体为压缩空气。 试验条件如表1所示。 文献提供了该外形在横向喷流时的喷流放大系数和压心系数。

图9 横向喷流试验模型Fig. 9 Model for transverse jet experiment

表1 横向喷流试验条件Table 1 Transverse jet experiment conditions

CFD验证采用的网格如10所示， 壁面和喷口附近区域的网格均进行了加密， 网格量约为1.5×106。

计算得到的横向喷流开启时的对称面Mach数和压力等值线如图11所示， 喷口附近的流线如图12所示。 由图可见， 计算较为清晰地捕获了喷流干扰的流场结构， 可以看到分离区内的分离涡和引射涡， 注意到喷流Mach盘后面的区域存在涡， 它是在Mach盘前后两个几乎垂直的剪切层的作用下形成的， 喷口前的两个旋涡对依然存在。

图10 横向喷流验证网格Fig. 10 Meshes for transverse jet

图11 横向喷流时对称面Mach数和压力云图Fig. 11 Contours of Mach number and pressure of symmetry plane with transverse jet

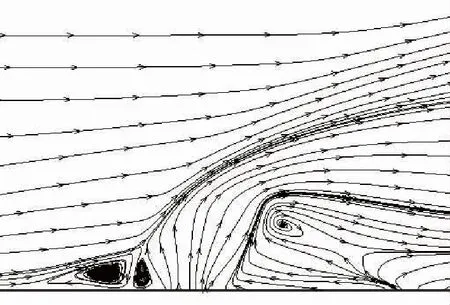
图12 横向喷流时对称面喷口附近流线图Fig. 12 Streamline near nozzle on symmetric plane with transverse jet

计算得到的喷流放大系数和压心系数与试验结果的比较如表2所示， 二者吻合较好， 证明了数值模拟方法的准确性。

表2 横向喷流CFD结果与试验结果比较Table 2 Comparison between CFD and experiment with transverse jet

由上述无喷流和有喷流状态的验证结果，可以确认求解方法和网格拓扑结构满足气动特性设计和评估的精度要求，可用于本文的对比研究。

3 分析与评估

本章根据有/无喷流时的CFD计算结果，对比分析发动机喷流对火箭基准气动特性和尾舵气动控制特性的影响。 由于火箭俯仰和偏航方向具有气动对称特性，本文分析主要针对俯仰方向。

3.1 喷流对火箭基准气动特性的影响

零侧滑、 零舵偏角的基准状态下，发动机有/无喷流时的火箭整体气动系数比较如图13所示，上述气动系数统计过程中，不含发动机喷管内部等部件。 对比可见，发动机喷流对火箭基准气动特性的影响主要有： (1)在亚声速和超声速段， 底部喷流对轴向力系数都有较为明显的减小， 亚声速状态减小约20%， 超声速状态减小约15%。 (2)在亚声速段，底部喷流使法向力系数有略微减小， 减小幅度最大不超过5%； 在超声速段， 底部喷流对法向力系数几乎没有影响。 (3)在亚声速段和超声速段， 底部喷流对弹体俯仰方向的气动静稳定特性也有0.2%～0.5%的影响， 且在亚声速段的影响比超声速段明显。

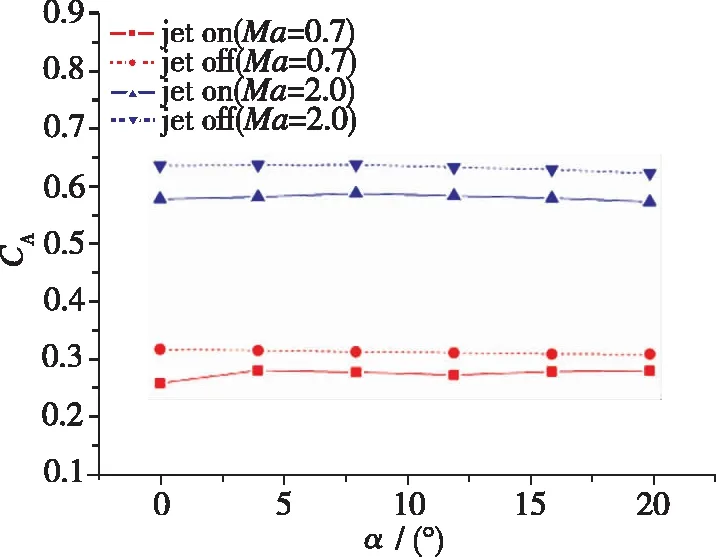
(a) Axial force coefficient， CA

(b) Normal force coefficient， CN

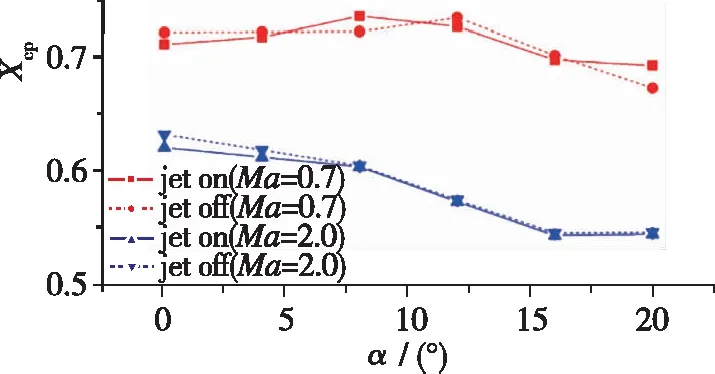
(c) Pressure center coefficient of pitching， Xcp图13 有/无喷流时火箭基准气动特性比较Fig. 13 Comparison of base aerodynamic characteristics of rocket with and without jet

有/无喷流时， 纵向对称面内的Mach数云图和流线图如图14, 15所示， 由图可见， 无论是亚声速还是超声速来流， 喷流在弹体尾部产生高温高压的膨胀流动， 对流场结构产生了明显的改变。

(a) α=0， with jet

(b) α=0， without jet 图14 有/无喷流时纵向对称面Mach云图和流线(Ma=0.7)Fig. 14 Contours of Mach number and streamline on longitudinal symmetry plane with/without jet (Ma=0.7)

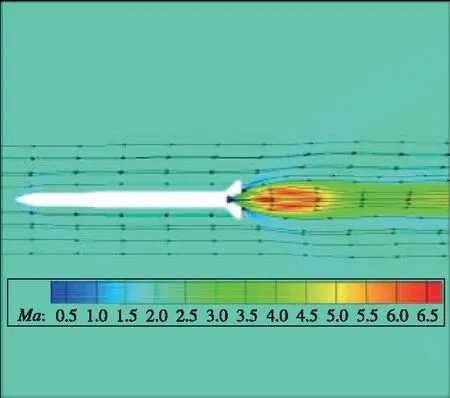
(a) α=0， with jet

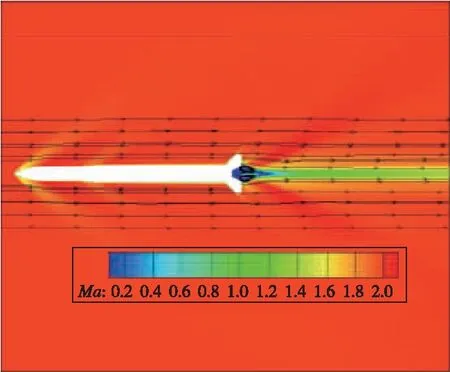
(b) α=0°， without jet 图15 有/无喷流时纵向对称面Mach数云图和流线(Ma=2.0)Fig. 15 Contours of Mach number and streamline on longitudinal symmetry plane with/without jet(Ma=2.0)

图16为有/无喷流时箭体表面压力系数云图及纵向对称面的Mach数云图的对比图， 图17为位于纵向对称面内的迎风、 背风面箭体母线上的压力系数随轴向位置x/L的变化曲线， 图18为轴向位置x/L=0.96处箭体横截面上的压力系数随周向角的变化曲线。 综合对比可见， 由于喷流的影响， 跨声速段时箭体后段较大区域的压力系数有所增高， 而超声速时仅在靠近喷流的较小区域的压力系数略微增大， 这是超声速段轴向力系数降低小于压声速段的主要原因。

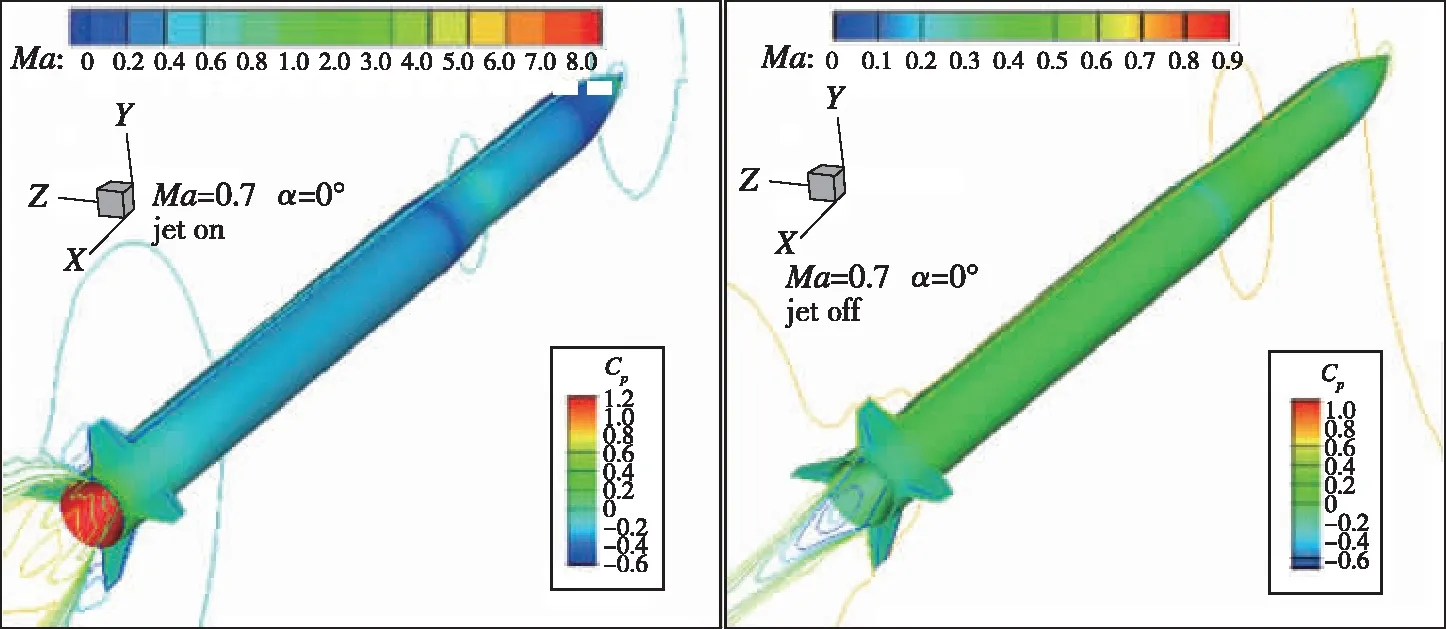
(a) Ma=0.7, α=0°

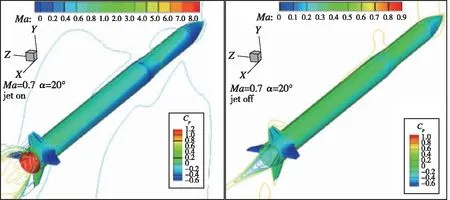
(b) Ma=0.7, α=20°

(c) Ma=2.0, α=0°

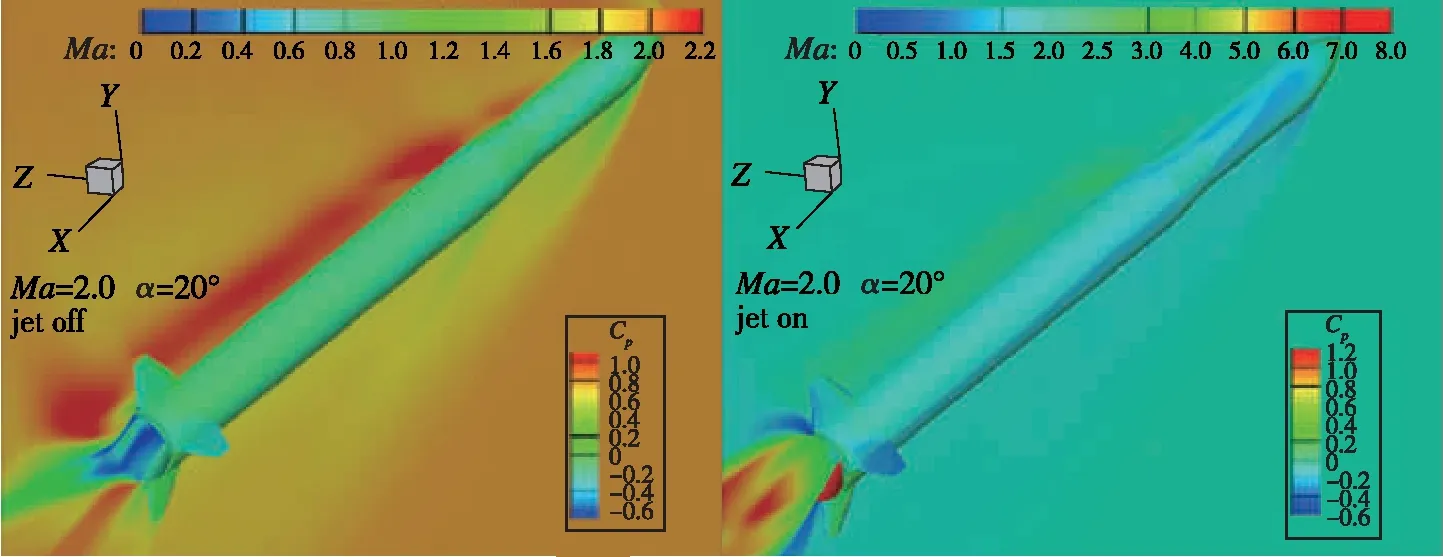
(d) Ma=2.0, α=20°图16 有/无喷流时箭体表面压力分布比较Fig. 16 Comparison of rocket surface pressure distribution with and without jet

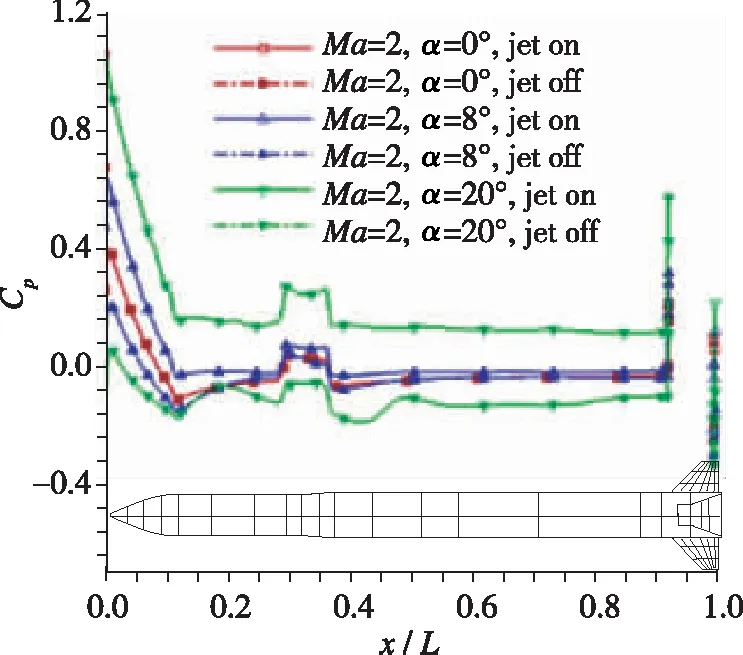
(b) Ma=2图17 有/无喷流时箭体纵向对称面母线上的压力系数Fig. 17 Pressure coefficients on the meridian of longitudinal symmetry plane of rocket with/without jet

有/无喷流时， 箭体轴向不同位置处横截面上的横流分布如图19， 20所示。 由图可见， 在亚声速段， 底部发动机喷流对箭体不同轴向位置处的背风面分离流动特征均有不同程度的影响， 喷流对箭体背风面的流动分离在一定程度上会起到抑制的作用; 在超声速段， 底部发动机喷流对箭体周围的流场影响微小。

(a) Ma=0.7

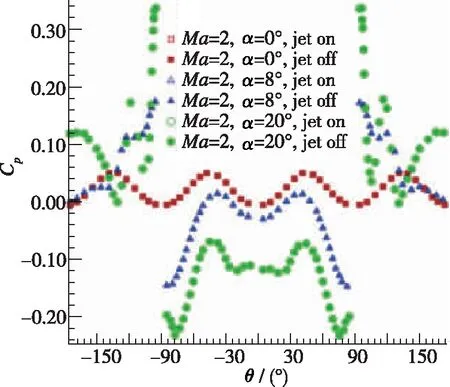
(b) Ma=2图18 有/无喷流时箭体轴向x/L=0.96横截面上的压力系数Fig. 18 Pressure coefficients on the cross-section of rocket at axial location x/L=0.96 with/without jet

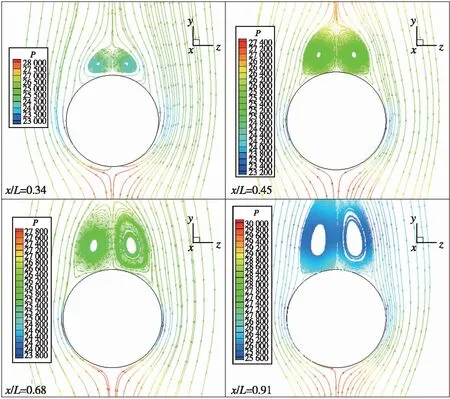
(a) With jet

(b) Without jet图19 有/无喷流时不同轴向横截面流线图(Ma=0.7)Fig. 19 Cross-sectional streamlines at different axial locations with/without jet(Ma=0.7)

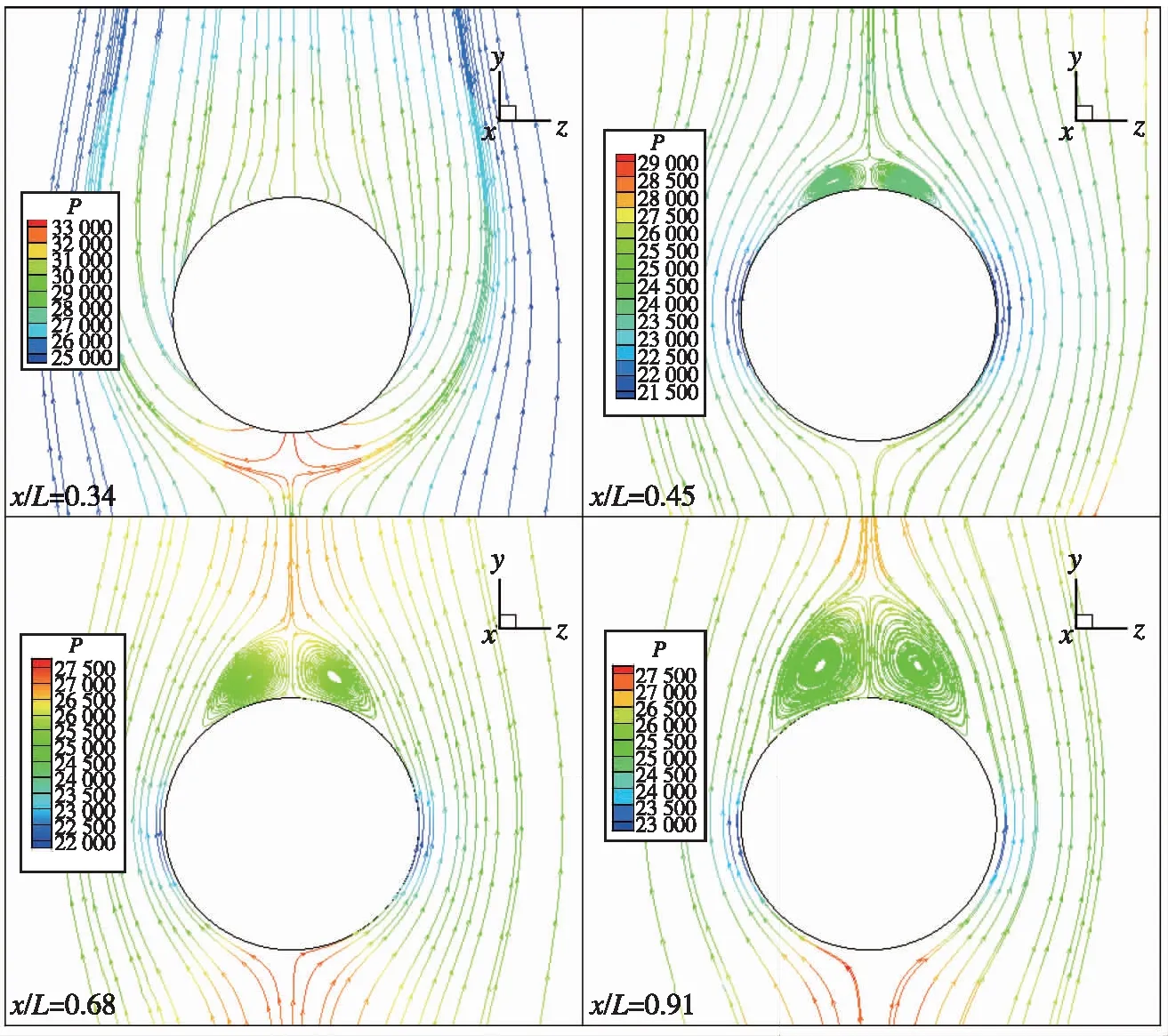
(a) With jet

(b) Without jet图20 有/无喷流时不同轴向横截面流线图(Ma=2.0)Fig. 20 Cross-sectional streamlines at different axial locations with/without jet(Ma=2.0)

3.2 喷流对尾舵气动控制特性的影响

通过对比有/无喷流状态下尾舵不同俯仰舵偏角时的火箭整体气动系数及尾舵舵效， 评估发动机喷流对尾舵气动控制特性的影响。 其中尾舵俯仰舵偏角dp的正负号定义如图21所示。

(a) Front view

(b) Rear view (deflection of leading edge of tail rudder)图21 尾舵俯仰舵偏角正负号定义Fig. 21 Definition of positive and negative deflection angles of tail rudder for pitch control

尾舵有俯仰舵偏、 发动机有/无喷流时的火箭整体气动系数的比较如图22, 23所示。 由图可见， (1)在亚声速状态下， 底部发动机喷流对尾舵俯仰舵效有明显改变， 舵效下降15%左右; 在超声速状态下， 底部喷流对尾舵俯仰舵效的影响较小。 (2)亚声速状态下， 发动机喷流一定程度上会增大尾舵的失速临界攻角。

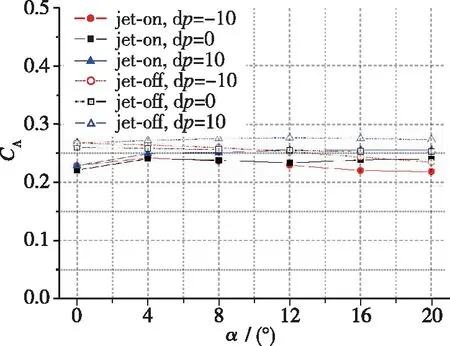
(a) Axial force coefficient， CA

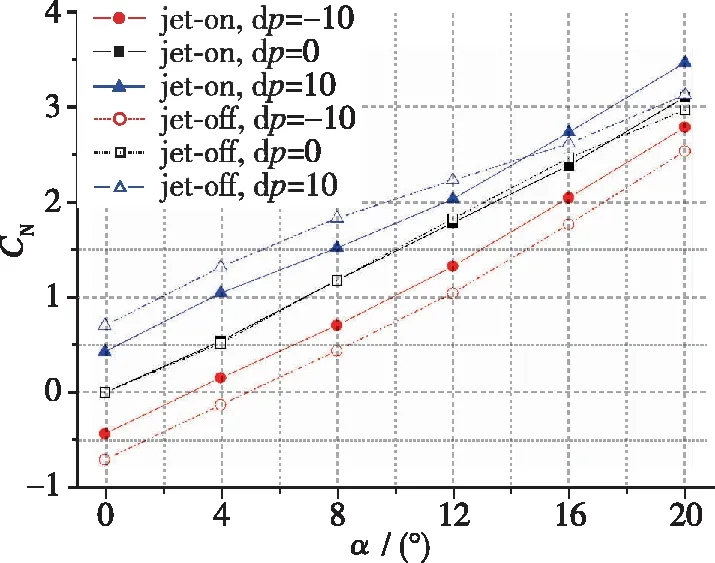
(b) Normal force coefficient， CN

(c) Pitching moment coefficient relative to centroid， Cmzg图22 尾舵有舵偏、 有/无喷流时火箭整体气动系数(Ma=0.7)Fig. 22 Aerodynamic coefficients of the rocket with/without jet (Ma=0.7, tail rudder has different pitch deflection angles)

(a) Axial force coefficient， CA

(b) Normal force coefficient， CN

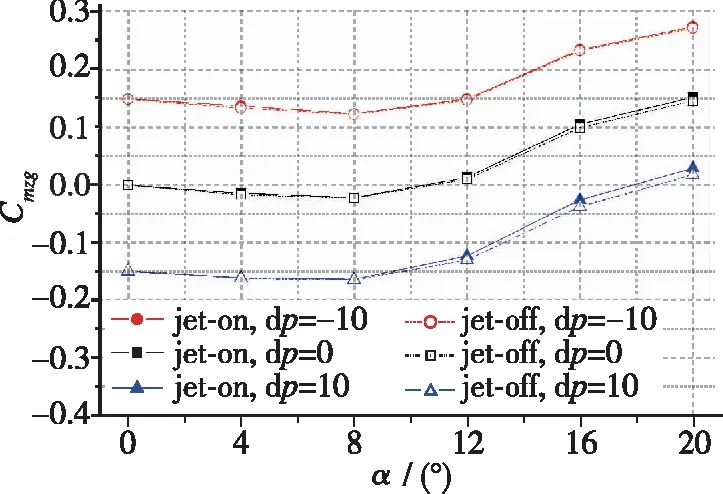
(c) Pitching moment coefficient relative to centroid， Cmzg图23 尾舵有舵偏、 有/无喷流时火箭整体气动系数(Ma=2.0)Fig. 23 Aerodynamic coefficients of the rocket with/without jet (Ma=2.0, tail rudder has different pitch deflection angles)

4 结论与启示

本文利用CFD仿真， 研究了火箭动力飞行过程中底部发动机喷流对其气动特性的影响， 主要结论与启示如下：

(1)发动机喷流对箭体基准气动特性有较为明显的影响， 最明显的是对轴向力系数的影响， 亚声速段和超声速段， 喷流引起的轴向力系数减小幅度为15%～20%， 基本与气动辨识结果一致。 亚声速段， 发动机喷流对箭体法向力系数和俯仰压心系数也有一定程度的改变。

(2)亚声速段， 发动机喷流对尾舵舵效有明显改变， 舵效下降15%左右; 超声速段， 喷流对舵效的影响较小。

(3)在火箭气动设计过程中， 喷流影响在风洞试验中较难模拟， 但影响又不可忽略。 为获取更为准确的气动特性， 需找到合适的考虑喷流影响的气动设计方法。 通过本文的研究， 可提供一种折中考虑喷流影响的气动特性设计方法， 具体为：

(a)开展常规风洞测力试验， 获取无发动机喷流影响的火箭气动特性

CX*(Ma,α,β,δ)

(b)开展CFD仿真计算， 获取无发动机喷流影响的火箭气动特性

CX**(Ma,α,β,δ)

(c)开展CFD仿真计算， 获取有发动机喷流影响的火箭气动特性

CX***(Ma,α,β,δ)

(d)根据CFD仿真计算获得的有/无喷流发动机喷流影响的气动数据， 得到发动机喷流对火箭气动特性的影响差量

ΔCX(Ma,α,β,δ)=CX***-CX**

(e)将风洞试验获得的火箭不考虑发动机喷流影响的气动特性与CFD计算获得的发动机喷流对火箭气动特性的影响差量叠加， 获得考虑发动机喷流影响时的火箭气动特性

CX(Ma,α,β,δ)=CX*+ΔCX

(4)根据之前的研究(见文献[17])， 若发动机喷管外露长度较为明显， 即便是不考虑喷流， 发动机喷管本身对火箭气动静稳定特性也有影响， 喷管摆动会产生可观的气动控制力矩。 结合两方面的研究结论， 精细化气动特性设计还需要考虑发动机喷管有摆角状态时的喷流影响。