基于进化算法和复合参数化方法的低速翼型优化
2022-10-14王顺顺
王顺顺, 郭 正
(国防科技大学空天科学学院, 湖南长沙 410000)
引 言
随着CFD的发展、 优化算法的日趋完善与计算能力的提升, 特定工况下气动外形优化成本越来越低, 使该技术的工程应用越发成为可能。气动优化可以显著提升飞行器的飞行性能和飞行品质, 对飞行安全、 飞行效率与经济性都有决定性影响[1]。翼型优化则是其中的重要内容, 波音公司的Garner等[2]认为, 对一架大型运输机, 在相同迎角下升力系数增加0.1, 即可因增大擦尾角缩短起落架而使飞机质量减少635 kg,而同一速度下, 最大升力系数增大1.5%则意味着载重增加3 000 kg。
翼型优化综合了实验方法、 参数化方法、 气动计算方法、 优化算法等多个学科。20世纪70年代Hicks等[3]首次将数值优化思想引入到翼型设计中, Yamamoto等[4]第一次将遗传算法引入到气动外形设计中, Quagliarella等[5]等利用遗传算法对翼型进行了系列优化设计, Jeong[6]将Krige模型结合遗传算法应用到翼型优化中, 国内如西北工业大学等单位也长期开展翼型优化相关研究, 周旺仪等[7]基于Krige代理模型与多目标遗传算法对增升装置进行多目标优化设计, 白俊强等[8]利用RBF动网格和改进粒子群算法进行多段翼优化,韩忠华等[9]总结了代理模型在气动优化方面的研究进展, 李润泽等[10]对“人在回路”思想在气动优化中的发展进行了综述, 高正红等[1]、 余雄庆[11]分别对飞机总体气动设计优化进行了回顾总结。总体来讲当前对于翼型气动优化的研究工作以验证优化方法为主, 面向工程应用的较少。
无人飞行器是目前航空领域研究的热点, 如美军的RQ-7影子无人机, 是美军旅团级作战单元单独获取地面情报的主力, 为100~500 kg量级的战术无人机, 该类无人机携带载荷较全、 质量较小, 应用最为广泛。但随着任务的不断拓展, 战术无人机对气动性能也提出了更高要求, 尤其对滞空时间与短距起降的需要日趋增加, 而当前无人机翼型研究主要针对高空长航时无人机, 对于战术无人机翼型研究较少, 本文研究的目的就是为该量级无人机设计高质量翼型, 优化的主要目标是综合提高其起降与巡航性能。
1 复合参数化方法
翼型参数化是用代数变量表征翼型几何形状的过程, 好的参数化方法可以用尽可能少的参数表征范围更广的翼型, 是翼型优化的基础。目前常用的翼型参数化方法有CST, PARSEC, Hicks-Henne等。CST方法的主要思想是使用由Bezier多项式构造的型函数修正类别函数以描述外形变化特征; PARSEC通过基函数的加权叠加分别表示翼型上下表面曲线; Hicks-Henne方法是将连续光滑的Hicks-Henne型函数加权叠加到初始翼型上去得到新的翼型轮廓。 廖炎平等[12]通过对比研究发现不同的参数化方法表现翼型的能力有较大的区别。此外当前的参数化方法已经可以用来对机翼甚至整机进行优化, 逐渐成为了气动优化领域的热点[13]。但单一的参数化方法往往存在不足, 比如光滑性与细节表现力是一对基本的矛盾, 王迅等[14]通过采用B样条叠加小波分解进行局部光顺的方法解决这个问题, 取得了较好效果。本文通过对在光滑性与细节表现性上各有优劣的两种参数化方法进行数值叠加, 吸收不同参数化方法的优势, 拓展翼型表现范围。
本文采用NACA 4位数翼型参数化方法与Hicks-Henne型函数法进行组合。其中NACA 4位数翼型是基于NACA变密度风洞实验数据提出的系列翼型, 它的特点是特征参数较少、 可解析描述、 翼型库丰富、 应用广泛可靠性好[15], 同时特征参数直接反映翼型几何特征, 便于结合飞机设计的结构要求对翼型的几何特征进行约束, 因此极适合作为优化的初始翼型库, 但由于翼型解析公式较为简单, 细节表现能力较弱。
为了弥补NACA 4位数翼型细节表现能力不足的缺点, 在其坐标基础上采用型函数线性扰动法叠加扰动, 形成复合参数化方法。翼型的形状由基准翼型和扰动型函数的线性叠加共同决定, 一般扰动型函数选用的是Hicks-Henne型函数[16]。原方法在翼型后缘表现方面有缺陷, 王建军等[17]对Hicks-Henne型函数进行了相关改进,弥补了这一不足。由于理论上可以采用任意高阶型函数, 具有很强的细节表现能力, 但选用参数范围过大时则可能会出现不适合工程应用的奇异翼型。同时该方法也无法对翼型几何特征进行有效控制, 所以一般用来进行小范围修型。其表达式如下, 其中ytop0、ylow0为原翼型上下翼面y坐标,xk为控制变化的变量。
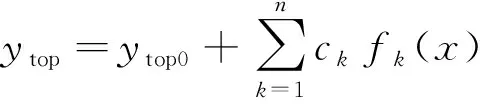
最终复合方法为将上两种方法进行数值叠加, 如下所示, 其中ylowf与ytopf为最终翼型的纵坐标,ytop1与ylow1分别为NACA 4位数翼型坐标, 后面的项为Hicks-Henne型函数数值扰动。
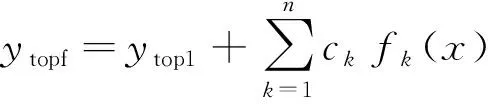
图1是3种参数化方法实现效果的对比, 可以看到单纯的NACA 4位数翼型细节表现不足, 但可靠性好并容易施加约束, Hicks-Henne型函数法容易出现奇异翼型,在某些情况下甚至出现不光顺的情况, 而通过两种参数化方法的叠加组合, 既能够保证翼型曲线的表现能力和翼型非奇异, 同时还可以约束弯度、 厚度等几何特征参数。
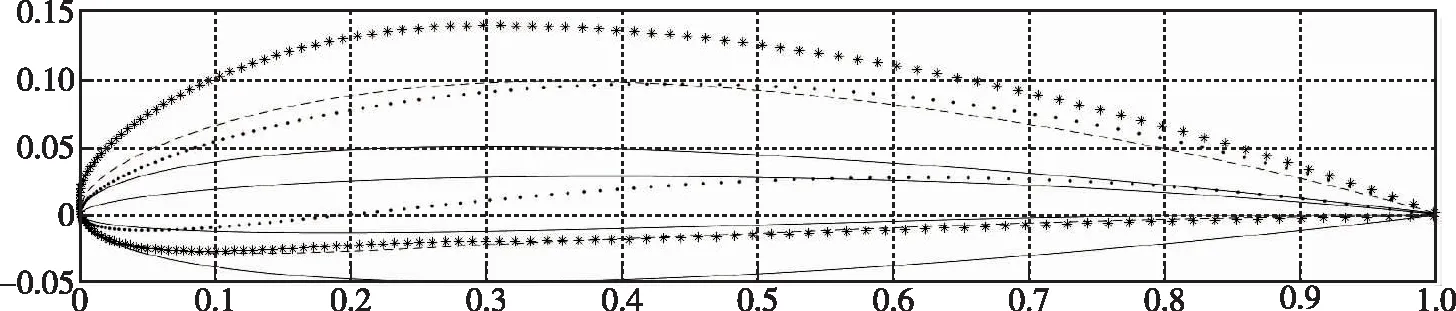
(a) Airfoil represented by NACA four-digit parameterization method

(b) Airfoil represented by Hicks-Henne shape functions
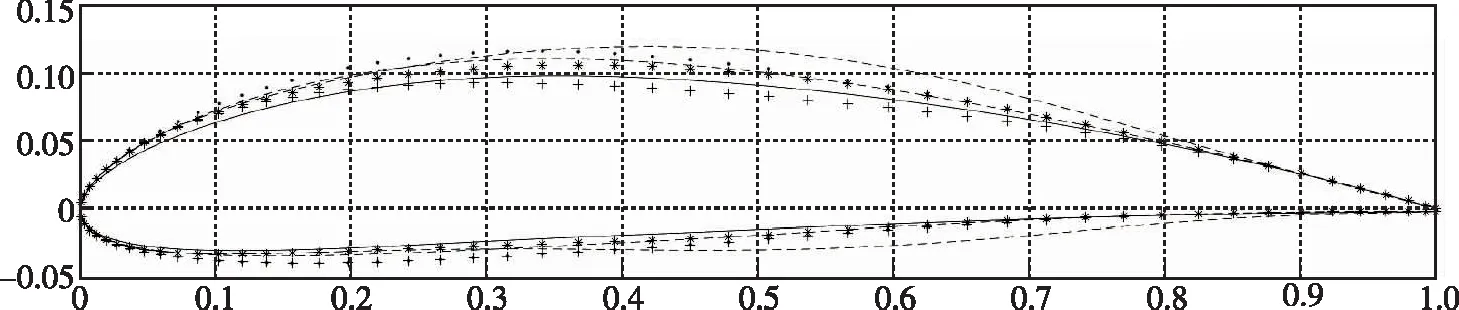
(c) Hicks-Henne functions superimposed on NACA 4412 airfoil图1 不同翼型参数化方法之间的比较Fig. 1 Comparison between different airfoil parameterization methods
2 分步计算方法
为了节省前期计算量, 尽快缩小优化范围, 初步优化采用Xfoil软件进行气动估算, 使用高阶的面元法和完全耦合的黏流/无黏流迭代方法计算阻力、 边界层转捩和分离[18]。尽管从理论上讲, 利用面元法进行流场模拟的近似等级最低, 但由于Xfoil发展早, 修正方法比较完善, 工程应用性较强, 成为目前使用广泛的气动估算软件。经检验, 在低Reynolds数和小迎角工况下Xfoil与CFD计算结果具有较好的一致性[19]。精细优化采用求解Reynolds平均 Navier-Stokes (RANS)方程进行流动数值计算, 利用软件脚本自动生成结构网格, 图2为生成的网格, 可以看到对于不同翼型自动生成的网格均有较好质量。
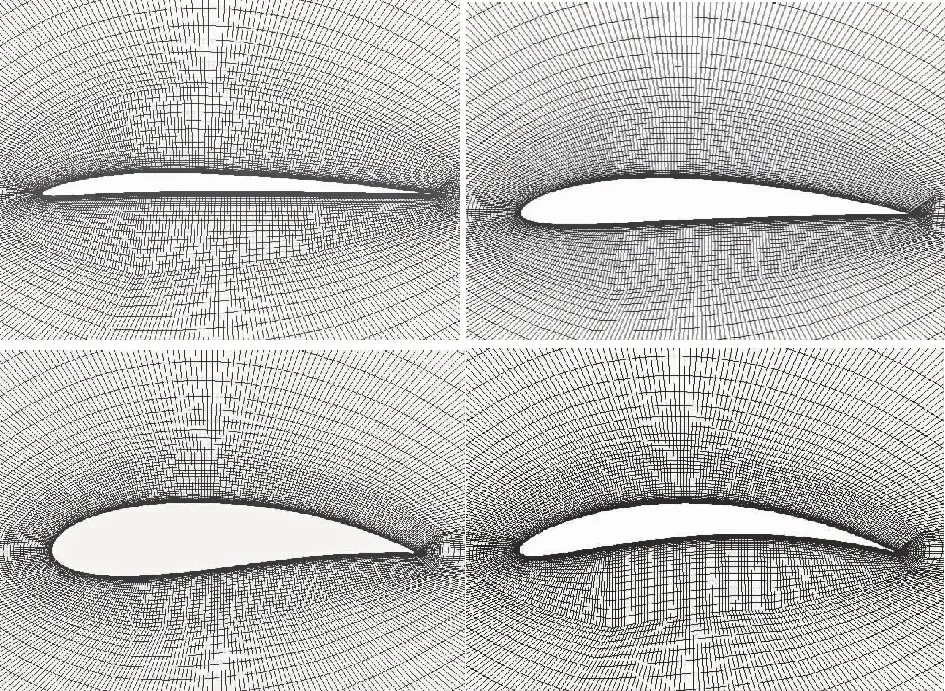
图2 生成的网格Fig. 2 Generated mesh
求解器采用Fluent软件, 湍流模型选择k-ωSST模型, 这是一种用来结合RANS方程可以有效计算翼型外流场的湍流模型, 计算对象为低速不可压流。图3为Re=1×106, 14°迎角条件下NACA 4412翼型的算例验证, 数据来自伊利诺伊大学低速风洞实验结果, 其中Cp与x分别为无量纲压力系数和长度。

图3 算例验证Fig. 3 Example verification
实际优化过程中发现采用分步计算可以较快地使翼型参数空间收敛到原范围的1/5, 小空间有利于后续优化算法进行精确寻优。考虑到气动估算基本不考虑时间成本, 所以采用估算方法与精确求解相结合的方法较全部采用精确求解方法进行优化耗费计算时间大大缩短, 同时优化精度不变。
3 优化算法与流程
翼型优化往往是典型的多目标优化问题,本文采用非归一化的NSGA-Ⅱ 算法。非归一化算法不用通过设置权重将多目标转化为单目标, 而是使所求解集的前沿与Pareto前沿尽量接近。NSGA-Ⅱ 算法是对NSGA算法的改良版, 优点在于探索性能更好, Pareto前沿前进能力增强, 收敛速度加快[20]。本文中群体规模取为40, 最大进化代数为200, 杂交率为0.9, 变异概率为0.01。图4为精细优化过程中的2°迎角升力系数收敛进程, 横坐标代表进化算法推进序列,可以看到在50代以后算法就已经收敛到最优值附近, 说明该算法的有效性。

图4 算法收敛进程Fig. 4 Algorithm convergence process
本文的优化流程为: ①根据适用工况确定优化目标、 约束、 初始翼型、 参数变化范围; ②利用Xfoil结合NACA 4位数翼型参数化方法进行初步优化, 选择一个合适的优化解作为下一步优化的起始值; ③确定优化参数范围, 采用求解Reynolds平均 Navier-Stokes 方程的气动解算方法进行精细优化; ④从最优解集中比较选择出合适的最优解; ⑤在上一步最优解上叠加Hicks-Henne扰动型函数进行细节优化; ⑥通过分析比较得到最优解, 检验优化结果, 流程结束。
4 优化案例
4.1 约束条件与初始条件
本节采用的初始翼型为NACA 5314, 弯度为5%、 弯度位置30%、 厚度为14%, 如图5所示, 是NACA 4位数字翼型中最大升力系数较高的低速翼型, 同时具有一定程度的缓失速性能。
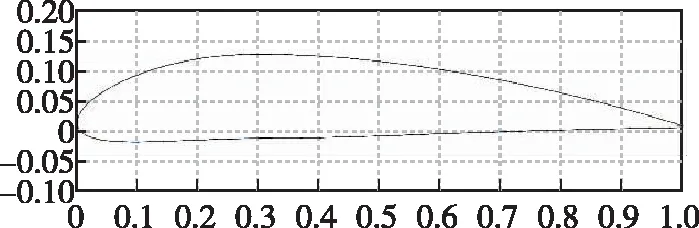
图5 初始翼型Fig. 5 Initial airfoil
本节设计工况为Re=1×106, 以下计算中Rey-nolds数保持不变, 为实现气动性能综合优化的目的, 考虑飞机起降与巡航阶段对于气动性能的不同要求及机翼结构的强度要求, 选择较高迎角下8°的升力系数CLα=8°与较低迎角下2°的升力系数CLα=2°和升阻比Kα=2°共3个参数作为优化目标, 以最大厚度t、 最大弯度位置xcamber、 最大弯度fmax为设计变量并确保翼型最大厚度t不小于5%, 可以表示为: 寻找一组设计变量x, 使
4.2 优化过程
初步优化中各参数上下各变化50%作为参数范围。最终图6为翼型初步优化前后对比, 可以发现翼型厚度明显降低, 同时弯度增大, 最大弯度位置后移。
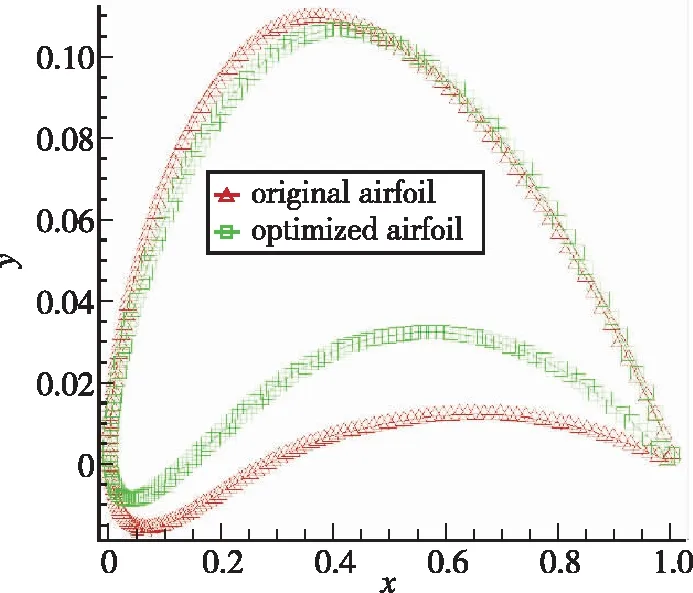
图6 初步优化前后翼型对比Fig. 6 Comparison of airfoils before and after preliminary optimization
图7为优化前后2°迎角下压力分布对比(单位为Pa), 图7(b)为优化后翼型,可以明显看到随着弯度增加后加载明显增大, 同时前缘厚度减小导致吸力峰强度略有降低。
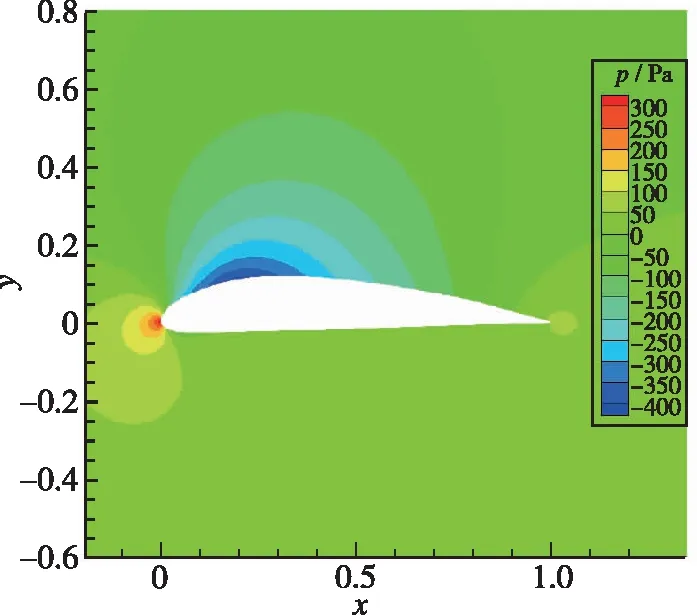
(a) Before optimization

(b) After optimization图7 压力分布对比Fig. 7 Pressure distribution comparison
初步优化后选取翼型的参数: 弯度为5.7%、 弯度位置在40.3%、 厚度为10.6%, 以得到的新翼型参数上下变化20%为新的参数范围, 通过求解RANS方程解算气动特性进行精确优化。精确优化得到的部分解集如图8所示, 得到的最优解有3个, 分别侧重于CLα=8°,CLα=2°,Kα=2°, 如图8所示, 3个结果分别标示为Op1, Op2, Op3, 但Op3拥有较均匀的气动特性优势故被选择为精确优化结果。
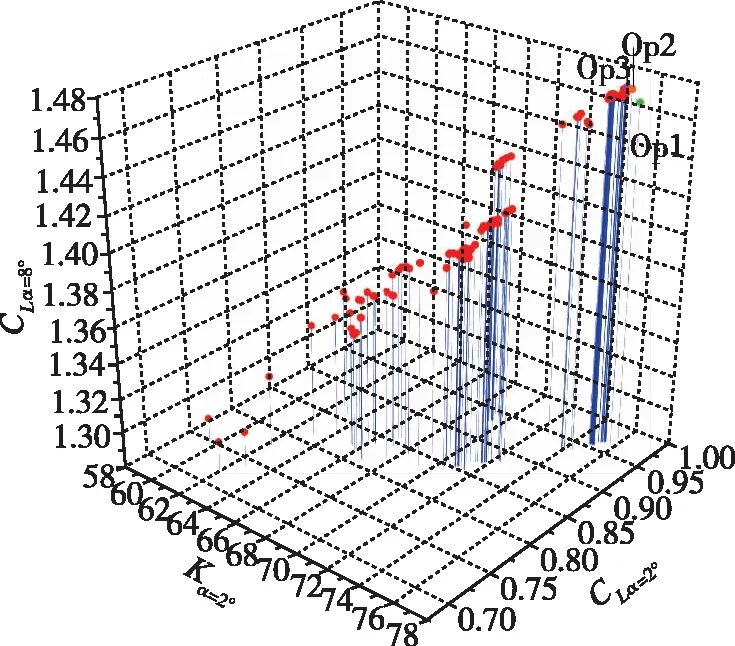
图8 精确优化的解集Fig. 8 Solutions of precise optimization
精确优化后翼型与原翼型对比见图9, 可以看到翼型厚度减小弯度增大, 最大弯度位置向后移。

图9 精确优化前后翼型对比Fig. 9 Comparison of airfoils before and after precise optimization
图10为翼型优化前后2°迎角下压力对比(单位为Pa), 图10(b)为优化后翼型, 上部曲率分布更加均匀、 前缘略平缓导致精确优化后翼型上部低压区范围明显增大, 同时弯度增大引起翼型下方压力增大。
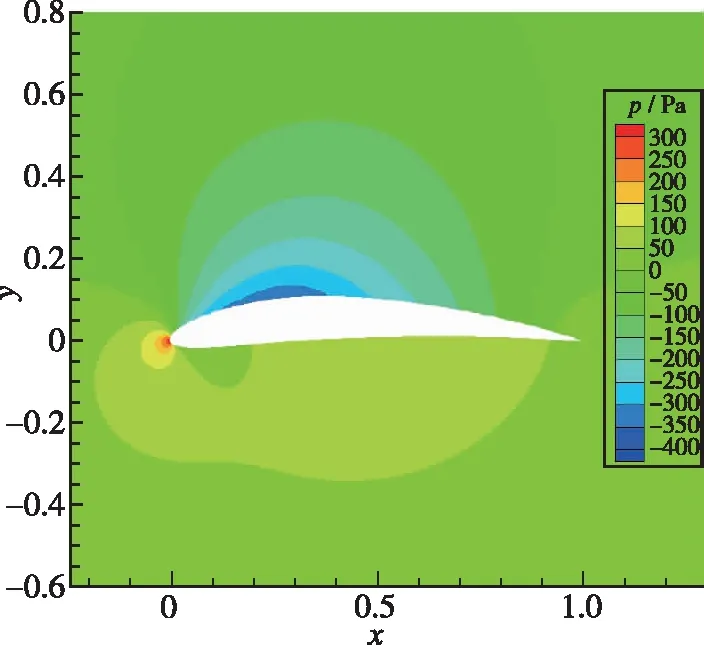
(a) Before optimization
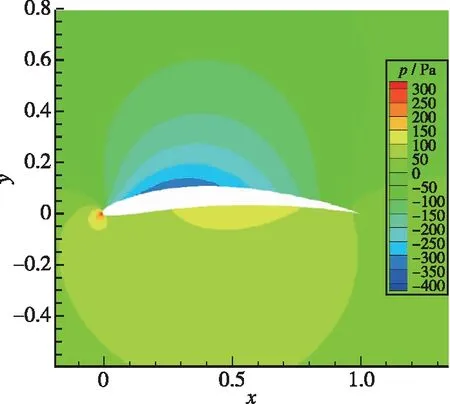
(b) After optimization图10 压力分布对比Fig.10 Pressure distribution comparison
结合大量计算数据还可以进一步分析翼型几何参数与气动性能之间的关系, 见图11。
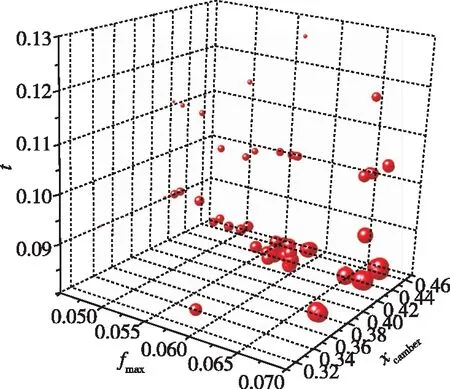
(a) KLα=2°
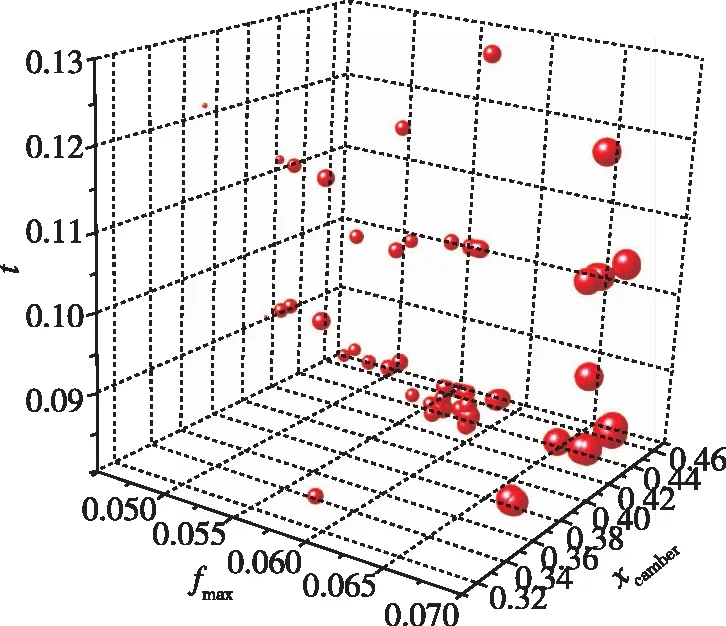
(b) CLα=2°
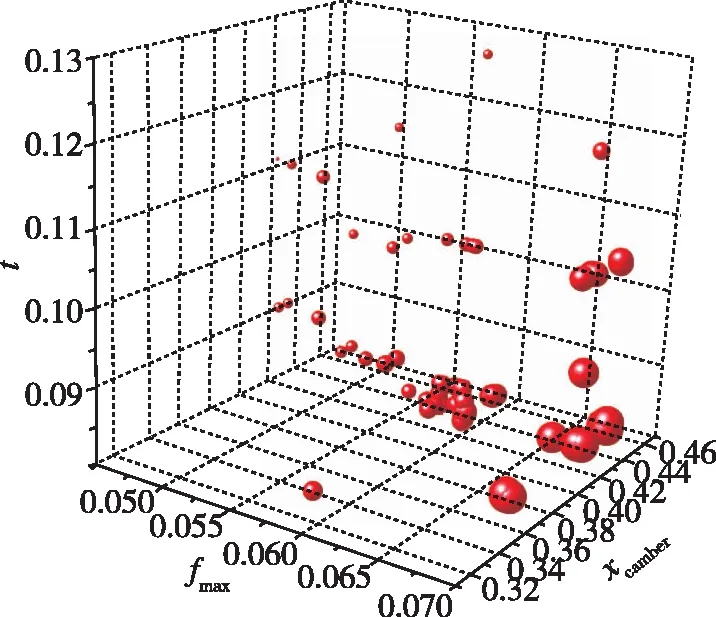
(c) CLα=8°图11 几何参数与气动性能的关系Fig. 11 Relationship between geometric parameters and aerodynamic performance
可以看到翼型的弯度对升力系数影响尤为明显, 这也是大量实验结果的结论, 而厚度的减小则会减少阻力系数, 提高升阻比。
对精确优化结果Op2采用改进型Hicks-Henne型函数摄动进行细节优化, 本文共设置12个摄动变量,上下翼面各6个, 每个控制变量的范围为-0.005~0.005, 各点在翼面上均匀分布。具体细节如图12所示。
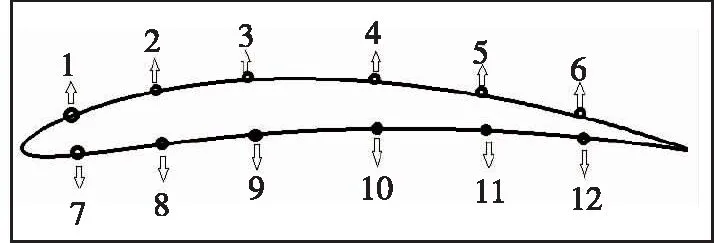
图12 Hicks-Henne型函数摄动Fig.12 Hicks-Henne function perturbation
细节优化的部分优化解集如图13, 其最优解也可以分为3类, 通过比较选择Op1作为最终优化结果。细节优化前后翼型对比见图14, 可以发现翼型弯度略有提升至8%, 最大弯度位置略有前移至40%, 翼型厚度略有减小至8%, 最大厚度位置前移至24%, 其2°迎角下压力分布对比(单位为Pa)见图15, 图15(b)为优化后翼型, 吸力峰强度与范围明显变大, 且翼型下方高压区扩大。
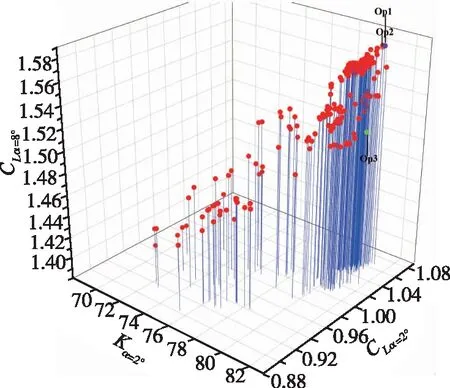
图13 细节优化的解集Fig. 13 Solutions of detailed optimization
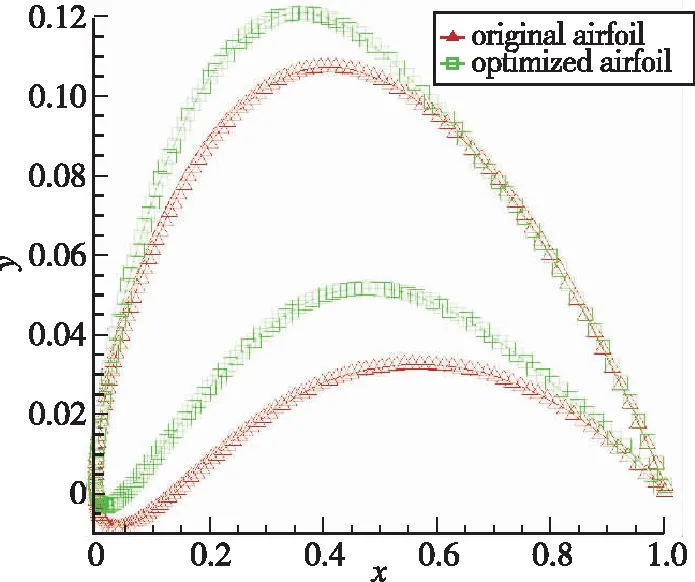
图14 细节优化前后翼型对比Fig. 14 Comparison of airfoils before and after detailed optimization
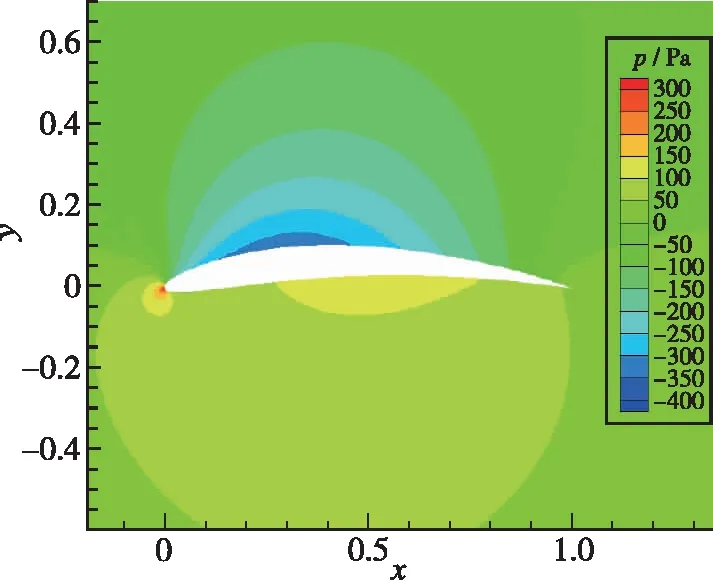
(a) Before optimization
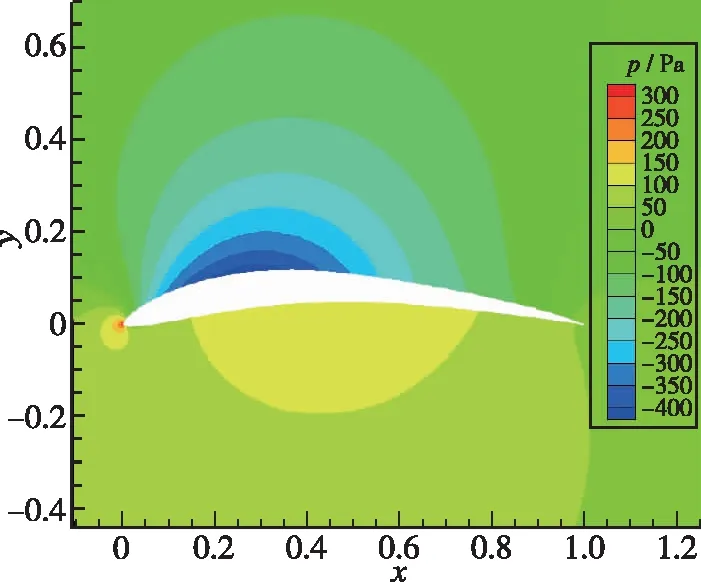
(b) After optimization图15 压力分布对比Fig.15 Pressure distribution comparison
4.3 优化结果
三轮优化结果对比如表1所示, 可以看到最终所有目标气动性能均有大幅度提升, 以2°迎角下的升阻比为例, 假设无人机在该迎角下巡航飞行, 根据布雷盖航程公式飞机航程与升阻比成正比, 则其最大航程也会比使用NACA 5314显著提高。优化结果见表1。

表1 优化结果对比Table 1 Comparison of optimized results
图16反映了优化前后两种翼型用Xfoil软件计算的气动性能之间的对比, 图16(a)可以看到经过优化的翼型在10°迎角以前的升力系数得到提升, 图16(b)中反映升力系数与升阻比的关系, 可以看到优化后的翼型在升力系数小于1.5时升阻大于原翼型, 这可以有效提升无人机的巡航性能。

(a) CL& α

(b) K & CL图16 优化前后气动性能对比Fig. 16 Aerodynamic performance comparison
5 结论
本文基于复合参数化方法结合进化算法, 对翼型在2°和8°两种迎角下的气动性能进行3轮优化, 优化后的翼型气动性能得到较大提升, 完全符合预定优化目标。
(1)实现了优化过程中对翼型几何形状的控制, 厚度保持在5%以上, 最大弯度低于9%, 满足了应用要求。
(2)采用多步翼型优化流程进行高效全局多目标求解, 翼型在两种工况下的升力系数、 升阻比都提高了20%以上。
