逆向喷流对双锥导弹外形减阻特性的影响
2020-12-28王泽江李杰曾学军王洪亮李志辉
王泽江,李杰,*,曾学军,王洪亮,李志辉
1.中国空气动力研究与发展中心 空天技术研究所,绵阳 621000 2.中国空气动力研究与发展中心 超高速空气动力研究所,绵阳 621000
高超声速飞行器潜在的军事和民用价值极大,是当今世界军事强国竞相研发的热点。飞行器在大气中作高速飞行时,气流受激波压缩和黏性阻滞作用,极大的黏性耗散使边界层内的气体呈现高压高温特性[1]。临近空间飞行时如何实现减阻和降热是高超声速飞行器设计面临的两个重要问题,具有极高研究价值。
高超声速飞行器受到的阻力主要来自波阻,热环境严重的部位通常是飞行器头部和迎风前缘,因此减阻和降热可以通过主动流动控制技术改变流场波系结构来实现[2-3]。作为主动流动控制技术的一种形式,逆向喷流一直受到业内研究者的关注。逆向喷流技术是利用逆向喷流与自由来流的相互作用,使流场的波系结构和涡系结构发生改变,以达到减阻降热的目的。
研究逆向喷流技术,无论是在应用还是在理论上都十分有意义,国内外学者为此开展了很多工作[4-6]。Finley[7]通过风洞试验,获得了在逆向喷流与超声速来流相互作用下,球头圆柱体和椭圆锥体模型的头部壁面压力分布以及不同喷流模态的纹影图像。Aso[8]和Hayashi[9-10]等进行了逆向喷流对球头圆柱体降热特性的试验研究和数值仿真。国内学者[11-20]从喷流压比、喷口尺寸、飞行迎角等角度,对球头体在逆向喷流作用下,头部流场结构、壁面压力和阻力系数的变化特性开展了很多研究,揭示了喷流模态转换机理,分析了壁面压力降低和阻力系数减小与喷流参数之间的变化关系。Deng等[21-22]研究了升力体头部逆向喷流的减阻效应、周期振荡和反馈回路等。
纵观现有逆向喷流数值仿真文献:研究对象多侧重于喷流对飞行器头部的影响,对飞行器整机,特别是对较大尺寸飞行器整机的减阻特性研究涉及较少;数值模拟时,大多直接给定喷流入口参数,计算得到喷流与自由来流相互作用的外流场并分析其减阻降热特性,仅有少量文献,如Daso[23]、Atiqa[24]等在研究逆向喷流对Apollo返回舱的减阻降热影响时对喷流的内外流场进行了完全模拟。
在逆向喷流应用设计时,若将逆向喷流对头部的减阻效果直接应用于飞行器整机,评估结果可能过于乐观。另外,以喷口为边界进行数值计算,在喷口给定均匀的喷流参数,忽略了喷管附面层的影响,获得的流场结构和喷流反作用力均可能与实际情况存在差别。
为此,本文以典型双锥导弹外形的球头、单锥(含头部)、双锥(全弹)为研究对象,采用CFD方法对逆向喷流的内外流进行了完全模拟;通过对不同研究对象在喷流马赫数、喷流压比等参数影响下的减阻特性进行对比分析,得到了有价值的结论,可为工程设计提供一定技术支持。
1 物理模型和数值方法
1.1 物理模型和网格设计
建模时,将喷流装置与飞行器固连作为控制体,对内外流场进行完全模拟。这有两点优势:一是考虑了喷管附面层的影响,使数值模拟更加符合物理实际;二是内流场从喷流驻室开始计算,可将喷流作用力转化为控制体内力,消除了将喷口作为计算边界而直接给定喷流马赫数和压力温度等参数所带来的计算误差。
采用导弹常用的钝头双锥轴对称外形,可同时分析逆向喷流对球头、单锥和双锥的减阻特性。球头与锥体同轴,头部半径rm=50 mm,半锥角θ1=16°,θ2=4°,单锥体(含头部)弹长L1=500 mm,双锥体(即全弹)长L2=3 000 mm,具体如图1所示。
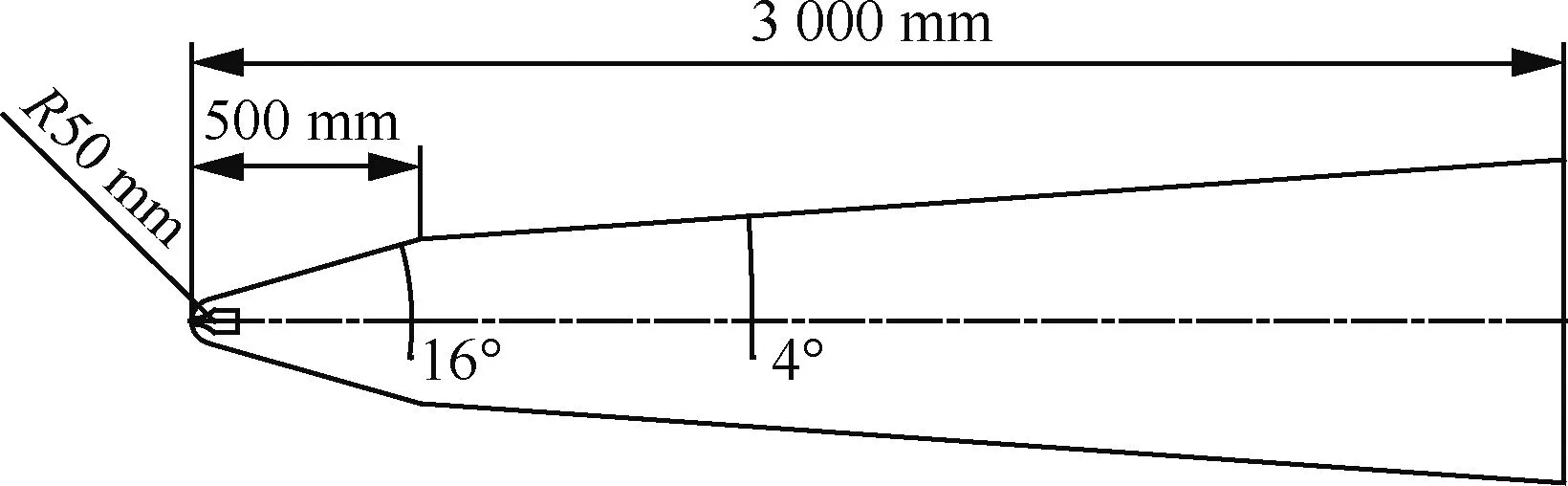
图1 双锥外形结构Fig.1 Conical outline structure
声速喷流采用收缩型面喷管(图2(a)),喷口最高马赫数Maj=1.0;超声速喷流采用锥形扩张拉瓦尔喷管(图2(b)),扩张角5°,喷口设计马赫数Maj=2.0。喷口半径rj均为6.25 mm,喷流驻室长度和直径均为50 mm。
图3为收缩喷管的计算域和网格图,超声速喷管与之类似,均采用结构网格。为适应黏性计算和激波捕捉需要,对局部网格采用了加密技术,近壁面网格y+≈1。
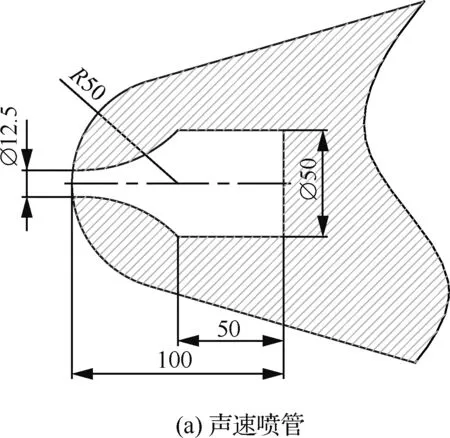

图2 喷流发生器结构Fig.2 Structure of jet generator

图3 计算域和网格图Fig.3 Compute domain and grid diagrams
设计了3套网格,其数量分别为62 000、76 400、 97 800。经无关性验证,最大误差<3%。为节约计算时间,本文选用数量为76 400的网格进行计算。
1.2 控制方程和边界条件
本文采用的控制方程为二维贴体曲线坐标系 下的可压缩非定常Navier-Stokes(N-S)方程:
∂Q/∂t+∂F/∂ξ+∂G/∂η+S=
(1)
式中:Q=[ρ,ρu,ρv,e]T/J,J为坐标变换雅克比矩阵,ρ为密度,u、v是速度分量,e为内能;F、G为贴体曲面坐标系下的对流通项;Fv、Gv为黏性扩散通项;S、Sv为源项。
数值离散时,对流项采用二阶迎风格式,扩散项采用中心差分格式;时间差分格式采用一阶精度的隐式格式;湍流模拟使用k-ωSST模型。
计算采用二维轴对称方法,计算域左边界为远场条件,取自由来流的参数值;右边界出口参数由上游值进行插值外推;飞行器表面、喷管内壁面和喷流驻室侧壁面设为绝热无滑移固壁边界;喷流驻室右边界的压力取喷流总压,速度为零。
计算条件为:自由来流马赫数Ma∞=4.0,压力p∞=9.02 kPa,温度T∞=216.65 K,来流迎角α=0°,喷流压比PR取1~30之间的16个状态值,喷流总温T0j=294 K。其中,PR=p0j/p0f,即喷流总压与自由来流正激波后皮托总压之比。
2 计算结果与分析
2.1 验证计算
为了验证网格设计方法和CFD算法的有效性,用文献[7]的试验条件进行了计算。图4给出PR=6.54时,计算得到的球头附近密度云图与文献[5]试验得到的纹影图。图5给出不同PR时,头部壁面无量纲压力静压p计算结果与文献[7]试验结果的对比。
从图4可知,计算获得的自由来流弓形主激波、喷流与来流接触面处的弧形末端激波、喷流侧边界剪切层的拦截冲波[25]以及喷流内部膨胀波的波系结构和激波位置与文献[7]试验纹影图对比一致。
从图5可知,计算与试验结果的差别很小,最大误差约2.4%。由此说明,本文所采用的物理模型、网格设计和数值模拟方法合理,计算结果准确。
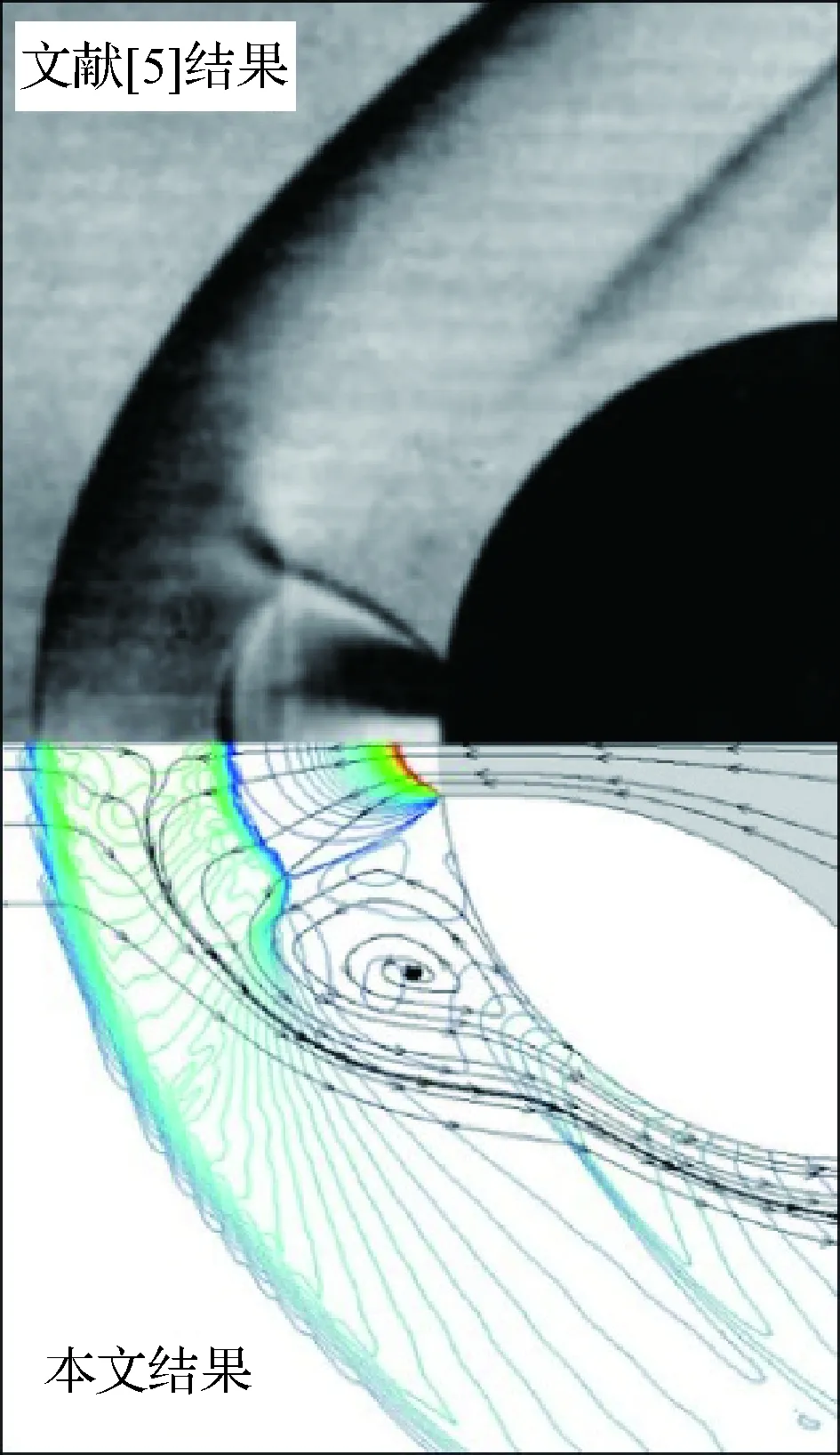
图4 PR=6.54时的计算密度云图和试验纹影图Fig.4 Schlieren of test and density contours of computation with PR=6.54
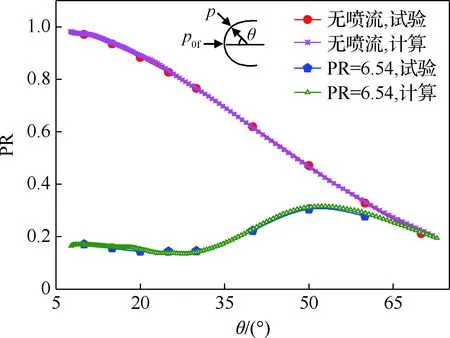
图5 头部壁面静压随PR的变化Fig.5 Wall static pressure varying with PR
2.2 流场结构
采用纯空气作为喷流介质,喷流驻室总温T0j=294 K,喷流压比PR=1,1.5,2,2.5,3,3.5,4,4.5,6,8,10,12,15,20,25,30(16个计算状态)。PR的选择依据是覆盖长短模态转换临界压比、最佳减阻压比等特征点,获得双锥导弹减阻效果的变化趋势。对声速和超声速两种喷管产生的流场进行了数值模拟。计算时设置了壁面压力等监视点,残差小于10-5时认为计算收敛,压力p收敛曲线如图6所示。
计算获得了与文献[7,12]相同的结论,即PR>1时可形成逆向喷流,头部弓形主激波形状发生改变,脱体距离增大;逆向喷流流场存在两种流动模态:长射流模态(图7(a))和短射流模态(图7(b))。逆向喷流在自由来流的作用下发生反转形成再附环,在喷流外侧出现低压回流区,使得迎风面压力下降,飞行器所受气动阻力减小。
喷流压比PR小于某个临界值时,出现长射流模态,射流中存在不稳定的多射流元结构,头部主激波形成椭圆形凸起,相当于在前面伸出一个杆状物体(图7(a));当PR大于这一临界值时,流场为短射流模态,此时仅有一个稳定的射流元。在喷流末端出现马赫盘,马赫盘与喷流侧面剪切层围成一个桶形激波,并随PR的增加而逐渐变强;当PR足够大时,末端激波足够强,使得椭圆形凸起的形状与主激波外形一致,相当于在头部生长了一个包覆鞘套(图7(b))。
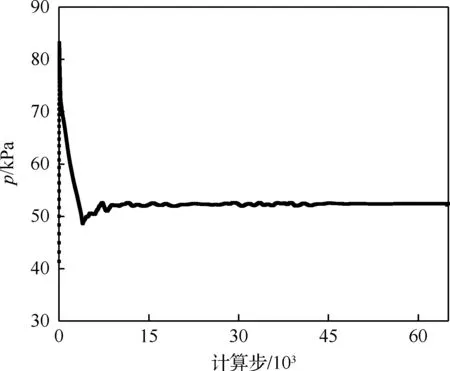
图6 压力收敛曲线Fig.6 Curve of pressure convergence

图7 两种流动模态的流场压力等值线图Fig.7 Pressure contour maps of two flow modes
短射流模态的流场结构较稳定,收敛时其壁面压力监测曲线的振荡特性很弱(图8(a))。临界值附近的长射流模态,流场结构呈现自激振荡特性,壁面压力和激波脱体距离等参数的波动较大。图8(b)为声速喷流在PR=1.25时壁面某点压力随时间的变化曲线。由图8(b)可知,振荡周期约0.32 ms, 最大振幅约为均值的10%,不稳定性很强。长模态时振荡慢但幅度大,短模态时振荡快但幅度小。振荡周期通过设置压力监测点可以准确求出。
为了减小喷流结构不稳定带来的误差,当喷流流场振荡特性比较明显时,在得到稳态流场后采用非定常方法继续进行计算,数据处理取一个振荡周期内的平均值。

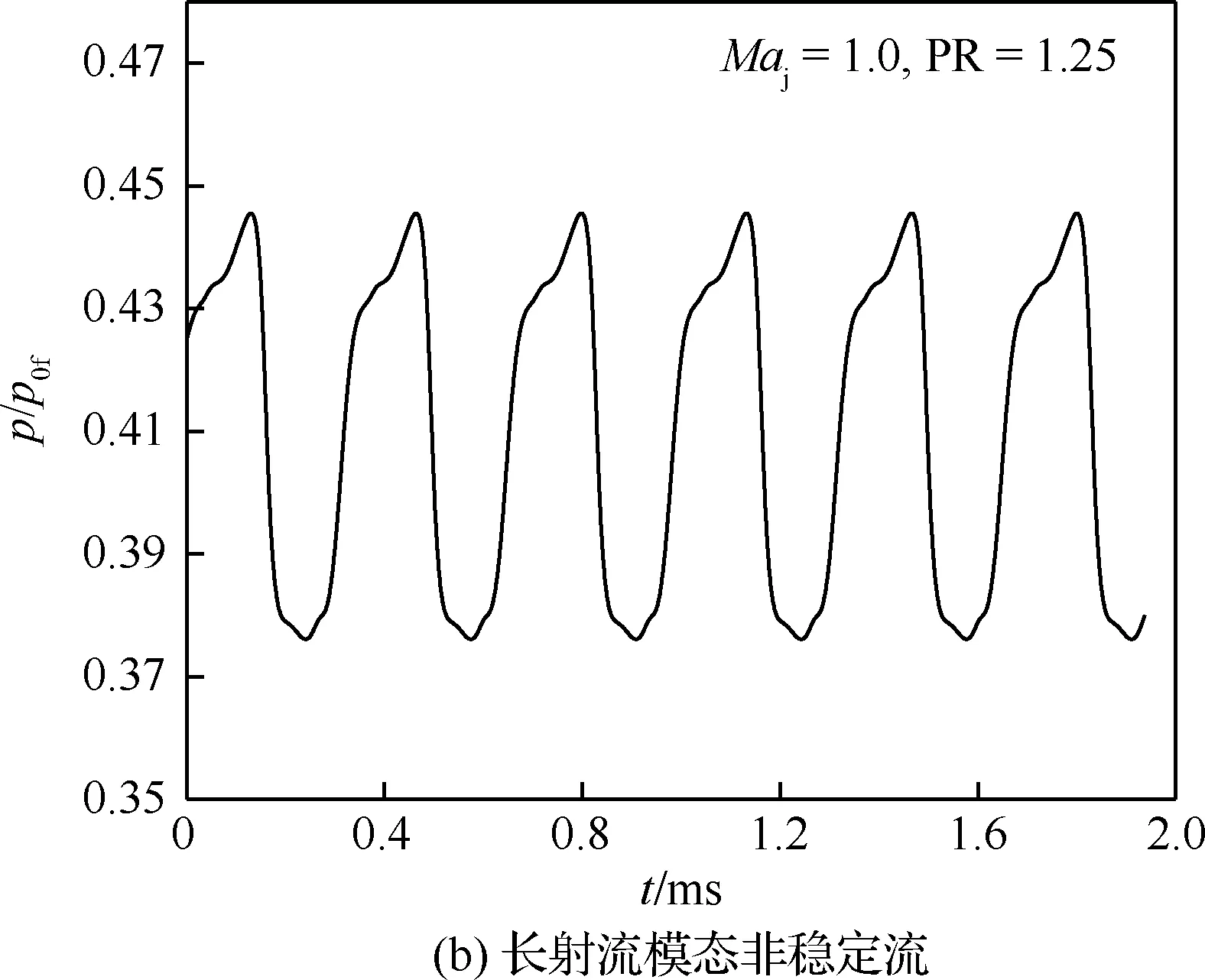
图8 壁面静压随时间变化历程Fig.8 Time-history of static pressure on body surface
2.3 逆向喷流减阻特性
逆向喷流在自由来流的作用下发生反转形成再附环,在喷流外侧出现低压回流区,使得迎风面压力下降,飞行器所受气动阻力减小;同时,喷流反作用力会抵消部分推力,等效于飞行器的阻力增加。这二者是相互矛盾的,因此工程应用时需要针对具体对象,对气动阻力和喷流作用力进行综合分析,确定合理的喷流压比,才能确保逆向喷流减阻有效。
为便于分析和叙述,本文定义减阻系数或阻力变化系数ΔCD为带喷流时飞行器阻力系数CDj与无喷时阻力系数CD0的相对变化量,即
ΔCD=(CDj-CD0)/CD0
(2)
减阻系数ΔCD<0表示逆向喷流具有减阻效果。带喷流时的阻力系数考虑了喷流的反作用力影响,即
D=Dout+Din+p0j·Sc
(3)
式中:Dout为飞行器所受气动阻力,;Din为喷管内壁面和喷流驻室内侧面的气动阻力;Sc为喷流驻室右端面的面积。
1) 逆向喷流对球头的减阻影响
图9给出双锥体前部球头的减阻系数ΔCD随喷流压比PR的变化曲线。图9中,实心图标减阻系数曲线代表声速喷流情况,空心图标减阻系数曲线对应超声速喷流情况。
从图9可知,研究对象为球头时,声速喷流和超声速喷流的减阻系数曲线均存在两个明显的最小值。采用声速喷流时,第一最小值出现在PR=1.5,此时阻力减小39.6%,喷流流场为长射流模态;第二最小值出现在PR=8,此时阻力减小42.4%, 喷流流场为短射流模态。采用超声速喷流时,两处最小值出现在PR=3.5和PR=8,阻力减小分别为43.7%和40.7%,前者为长射流模态,后者为短射流模态。
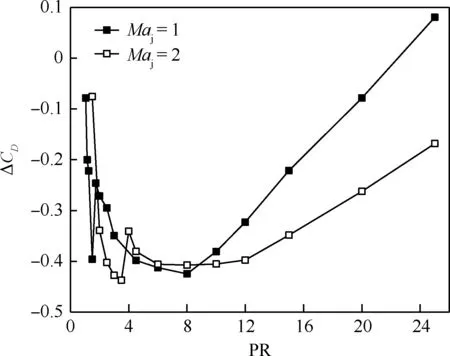
图9 双锥ΔCD随PR的变化曲线Fig.9 Curves of ΔCD of double-cone with PR
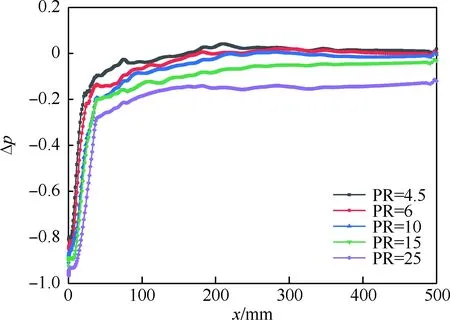
从图9可知,在2 在PR>8以后,喷流反作用力开始占据主导地位,其增加量甚至会超过气动阻力减少量,减阻效果逐渐降低直至消失。如声速喷流在PR=25时,ΔCD=0.08,即阻力不降反增,已失去减阻效果。 2) 逆向喷流对单锥和双锥的减阻影响 图10为声速喷流和超声速喷流时,单锥与双锥的减阻系数ΔCD随PR变化的对比曲线。从图10可知,无论是单锥还是双锥,在喷流长/短模态转换的临界压比附近(Maj=1时,PR=1.5;Maj=2 时,PR=4),减阻系数ΔCD均存在一个跳跃,但此时的减阻效果并不是最佳。随着PR的增大,ΔCD曲线还在继续下降,减阻效果继续增强,说明该条件下的短射流模态的减阻效果明显比优于长射流模态。 在PR=1~30范围内,单锥/双锥的ΔCD曲线都只有一个最小值,但达到最小值的压比不同(Maj=1时,PR=12;Maj=2时,PR=25),此时的喷流流场均为短射流模态。从而说明,在来流条件、喷口尺寸相同情况下,对于大尺寸飞行器,要得到比较好的减阻效果其喷流压比研究对象仅为球头时更高。 图10 单锥和双锥ΔCD随PR的变化曲线Fig.10 Curves of ΔCD of single-cone and double-cone with PR 由图10可知,喷流Maj=1时,在PR=1~8区间,单锥和双锥的ΔCD曲线下降均较快,减阻效果迅速增强;PR=8~12时,ΔCD曲线明显变缓,减阻效果增加不明显;PR>12后,ΔCD曲线逐渐上升,减阻效果随PR的增加逐渐变差。喷流Maj=2时,ΔCD曲线的变化规律与Maj=1相似,但对应的压比不同。在PR=1~15区间下降较快,减阻效果增强明显;在PR=15~25区间平缓,减阻效果增加不明显;PR>25以后,减阻系数曲线急剧上升,减阻效果变差。 从图10可知,当PR<18时,声速喷流的减阻效果优于超声速喷流;PR>18时,超声速喷流的减阻效果优于声速喷流。考虑到喷流速度、压比越大,流量越多,所需储气瓶体积越大,工程应用时应优先采用声速喷流,主要原因有两点:一是声速喷流的减阻效果稍优于超声速喷流(单锥和双锥的声速喷流最大减阻量分别是12.7%和5.9%, 超声速喷流最大减阻量分别为11.9%和5.4%);二是在来流条件、喷口尺寸相同情况下,声速喷流减阻系数曲线最小值对应的压比(PR=12)和流量(660 g/s)均小于超声速喷流的压比(PR=25)和流量(815 g/s),所需的储气瓶装载空间相对较小。 3) 对比分析 由图9、图10可知,无论是声速喷流或是超声速喷流,均可对球头、单锥和双锥产生减阻效果,且其ΔCD曲线随喷流压比PR均呈现先降低后升高的变化过程,均存在一个最佳喷流压比使其减阻效果最好,具体数据见表1。从表1可知, 表1 不同工况的最佳喷流压比和最大减阻值Table 1 Best PRs and largest drag reduction values 球头的最佳喷流压比最小,单锥次之,双锥的最佳喷流压比最大。相同条件下,研究对象为球头时,逆向喷流的减阻效果可超过40%;单锥的最大减阻效果约12%;双锥的最大减阻效果则只有6%左右。 也就是说,对于完全相同的计算条件,当逆向喷流作用的控制体不同时,所产生的减阻效果差异很大。对于本文长约3 m的典型双锥导弹外形,逆向喷流可产生约6%的减阻效果;控制体仅为双锥导弹头部时,逆向喷流产生的减阻效果超过了40%,减阻效果乐观。在工程应用时,若将喷流仅对飞行器头部作用时所表现出的优异的减阻特性直接推广至飞行器整机,评估结果过于乐观,甚至可能得出错误的结论。 定义压力变化系数Δp为壁面上某点带喷流时壁面压力pjet与无喷流时壁面压力poff的相对变化,即 Δp=(pjet-poff)/poff (4) 图11 球头和锥体壁面Δp随PR的变化曲线Fig.11 Curves of Δp on wall with PR 本文以声速喷流对单锥体作用特性为例进行分析。图11给出了声速喷流时,单锥体壁面Δp随PR的变化曲线。从图11可知,逆向喷流使头部压力下降80%以上,最大超过90%;在球-锥连接处(x≈36 mm), 压力下降10%~30%。当PR<6时,锥体前段(36 mm 综合图9~图11可知,声速和超声速喷流对单锥、双锥的最佳减阻喷流压比和壁面压力特性都具有相同的规律,即最佳喷流压比(如图11中PR=10的蓝色曲线)发生在逆向喷流刚好使飞行器全部表面的压力均开始下降的时刻。 1) 无论球头、单锥还是双锥,逆向喷流流场都存在长、短射流两种模态。球头在小压比长射流模态时的减阻效果最佳;对于单锥和双锥,在大压比短射流模态时的减阻效果均明显优于小压比长射流模态。 2) 存在一个最佳压比,使得逆向喷流的减阻效果最好。最佳压比发生在逆向喷流刚好使机体全部表面压力开始下降时刻。球头的最佳压比远小于单锥或双锥。逆向喷流压比过大时的减阻效果反而变差,甚至出现阻力系数不降反增的状况。 3) 计算条件、喷口尺寸相同情况下,控制体选取不同时,逆向喷流减阻效果的差异很大:球头的减阻效果可超过40%、单锥最大减阻效果约12%、双锥最大减阻效果只有6%左右。若将逆向喷流对头部的减阻特性直接推广至飞行器,评估结果过于乐观。 4) 综合考虑最佳减阻效果、达到最大减阻效果时的最佳喷流压比低、流量小、所需储气瓶体积等因素,逆向喷流主动控制技术工程应用时应优先选用声速喷流。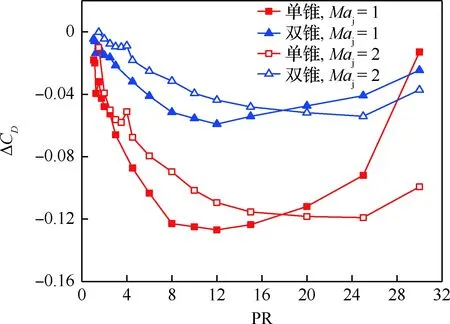

2.4 最佳喷流压比与壁面压力特性
3 结 论
