稀薄气体流动非线性耦合本构关系研究进展
2022-10-14袁震宇陈伟芳江中正赵文文
袁震宇, 陈伟芳, 江中正, 赵文文
(浙江大学航空航天学院, 浙江杭州 310027)
引 言
为了更好地研究跨流域多尺度问题, 一般可以根据Knudsen数将流域划分为不同的区间。Knudsen数是由丹麦物理学家Martin Knudsen首次提出的无量化参数, 其定义为分子平均自由程与流动特征长度的比值, 以下简记为Kn。按照Kn的大小, 流动可以划分为4种流域: 连续流(Kn<0.01), 滑移流(0.01
为了提供一种可靠并能够实现稳定计算的高阶流体动力学模型, Eu[12-15]从广义流体动力学的基本理论出发并结合非平衡集成方法, 提出了一组广义流体动力学方程组(generalized hydrodynamic equations, GHE)。在建模过程中, Eu首先通过构造一套指数型非平衡态分布函数, 巧妙地将非平衡态到平衡态的熵增特性与宏观非守恒量的耗散过程紧密结合起来。在此基础上, 将该指数型分布函数代入Boltzmann碰撞项进行建模。最终, 得到了严格满足热力学熵增定律的广义流体动力学方程组。然而, 该方程组的高度非线性与强耦合性, 使其仅限于研究一维线性化问题[16]。例如, 声波在双原子气体, 如N2, H2, D2, HD中的吸收与色散问题。为了将GHE拓展至实际问题的研究中, Eu通过提出绝热假设和封闭理论分别对高阶非守恒量的时间导数项和高阶矩的通量项进行简化处理。最终, 得到简化的广义流体动力学方程组, 并成功运用到单原子[17]和双原子气体[18-19]的一维激波结构模拟中。当计算Mach数从1.2~10变化时均能得到光滑激波解。为了构建一套更易于求解的纯代数形式的方程组, Myong[20-21]通过忽略简化的广义流体动力学方程组中非守恒量的梯度项与热流和速度梯度的点乘项, 建立了非线性耦合本构关系(nonlinear coupled constitutive relations, NCCR)模型。相比于传统N-S方程的线性本构模型, NCCR方程中应力与热流的表达形式具有高非线性与强耦合性的特征。虽然NCCR为捕捉非平衡流动的非线性特征提供了坚实的理论基础, 但是相比于传统的线性本构体系, 其求解难度大大增加。为了有效地求解NCCR方程, Myong提出了一种解耦求解算法。该方法的主要思想是将一个多维问题分解为各个方向独立的一维问题, 最终以线性叠加的方式得到NCCR方程的收敛解。解耦方法已经成功地将NCCR方程组运用到高超声速非平衡流动问题中, 如一维激波结构[20]、 平板绕流[22]等。在此研究基础上, Myong通过增加附加体积应力的非线性演化方程, 将NCCR方程进一步拓展到双原子气体的研究中。有效地模拟了双原子气体一维激波结构以及二维钝头绕流等问题[21], 并取得了与实验或DSMC方法较为吻合的结果。
然而, 解耦思想忽略了真实流动中各方向的耦合特性, 同时弱化了NCCR方程本身固有的耦合特征。在实际的研究过程中也发现, 解耦求解方法对于三维复杂流动问题存在收敛困难以及计算不稳定的缺陷。尤其在尾部膨胀流域, 极易出现负密度等非物理现象。为了充分地发挥NCCR方程的耦合特性, 提出了一种耦合迭代算法[23-24]。该方法充分结合了不动点迭代法与Newton迭代法各自的优势, 无论在强压缩区或膨胀区均能得到NCCR方程的收敛解。大量的数值验证结果表明, 耦合算法不仅在激波结构[25]、 圆柱绕流[23]、 钝头绕流[26]等标准模型上得到了有效的验证, 同时, 也能够成功地拓展到高超声速复杂工程问题的流场结构和气动力热预测中, 如空心扩张圆管流动、 HTV-2飞行器[26]和Apollo返回舱等。为了进一步提高NCCR方程计算气动力、 热的精度, 结合耦合求解算法提出了关于NCCR方程的高精度边界条件[27]。关于NCCR方程的拓展研究还有很多, 例如, 在NCCR的本构体系中考虑了非定常项用于研究气动加热问题[28-29]; 在气体动理学格式[30-31]的框架下, 求解NCCR方程, 提出的拓展气体动理学格式[32]等。然而, Myong提出的传统NCCR方程对热通量演化方程的简化处理, 在一定程度上降低了原始方程的计算精度。为了使NCCR发挥出更高的计算精度, 提出了一种改进的NCCR+方程[33], 并同样采用耦合求解的方法对NCCR+方程进行了有效的求解。通过模拟Apollo返回舱再入过程迎风面强激波压缩流和不同扩张拐角高超声速膨胀流, 表明NCCR+方程的确能够在强激波压缩区域和膨胀区域提高传统NCCR方程的计算精度,具有更强的非平衡流动模拟能力。在这些研究的基础上, 考虑到高超声速流动中不仅存在多尺度效应, 同时也存在显著的热力学与热化学非平衡效应, 于是将NCCR方程的非线性效应与多物理效应充分地结合, 构建了NCCR方程的双温度计算模型[34], 以及NCCR方程的热化学反应的耦合计算模型[35]。这些模型已成功地运用于高超声速复杂外形的计算, 用于揭示稀薄气体效应与真实气体效应的耦合作用机理。本文将围绕NCCR方程的理论研究与工程应用两方面, 对近年来NCCR方程的研究进展进行综述性回顾。
1 NCCR方程理论基础
1.1 广义速度矩
对于流动问题, 通常可以将流场中的宏观物理量分为守恒量和非守恒量, 宏观量与微观量的对应关系可以表示为
Φ(k)=〈h(k)f〉
式中, 角括号代表对气体分子在整个相速度空间的积分,Φ(k)代表两组宏观物理量,h(k)为这些宏观量对应的微观表达式。
对于守恒量, 其宏观与微观定义如下
Φ(1)=ρ,Φ(2)=ρU,Φ(3)=ρe
式中,ρ,U和ρe分别为气体的宏观密度、 速度和内能,m,ξ和Hrot分别表示粒子的微观质量, 速度和转动Hamilton算子(仅针对双原子气体)。
非守恒量的宏观与微观定义如下
Φ(4)=Π,Φ(5)=Δ,Φ(6)=Q
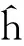
其中,I代表单位张量。
1.2 非守量的演化方程
由于守恒量的演化方程严格满足质量、 动量、 能量守恒关系, 且有明确统一的表达形式, 不再赘述。而非守恒量的演化方程, 由于建模方式的不同, 最终的表达形式不尽相同。为了对非守恒量的演化方程进行建模, 同时将非平衡态到平衡态的熵增特性与宏观非守恒量的耗散过程紧密结合起来, Eu提出了一种指数型非平衡态分布函数[12]。在无外力作用下, 单组分气体分子的非平衡态分布函数表达形式为
其中,T,kB分别代表温度和Boltzmann常数,μ是归一化因子,X(k)是与宏观量有关的系数, 其表达形式为
X(4)=-Φ(4)/(2p)=-Π/(2p)
X(5)=-3Φ(5)/(2p)=-3Δ/(2p)
Eu基于该非平衡态分布函数, 并通过碰撞累积量展开的方式对Boltzmann的碰撞项建模。并在此基础上, 结合广义速度矩的演化方程, 最终得到了非守恒量的演化方程, 如下
(1)
(2)
(3)
其中,ψ(1),ψ(2),ψ(3),ψ(p)代表高阶矩;γ′=(5-3γ)/2;q(κ)是非线性耗散项, 其具体表达形式为sinh(κ)/κ; sinh(κ)是双曲正弦函数, sinh(κ)=(eκ-e-κ)/2,κ通过Rayleigh-Onsager耗散方程给定, 其表达形式为
从其表达形式可以看出,κ是一个非常核心的参数, 该无量纲参数综合了与气体相关的物理信息: (1)与气体属性相关的信息, 其中包括分子质量(m)、 直径(d)、 剪切黏性系数(η)、 体积黏性系数(ηb)和热传导系数(λ); (2)与流场宏观物理量相关的信息, 其中包括温度(T)和压力(p); (3)与非守恒量相关的信息, 包括应力(Π)、 附加体积应力(Δ)和热流(Q)。
1.3 高阶矩封闭与绝热假设
(1)高阶矩封闭
通过式(1)~(3)不难发现, 虽然得到了高阶矩的演化方程, 但是广义流体动力学方程组依然是一个有待封闭的系统。因为高阶矩依然没有明确的表达形式, 所以为了封闭方程组必须对高阶矩进行建模。Eu为了封闭上述方程组, 提出了一套有别于Crad封闭的简单封闭方法[17], 即假设高阶矩为零
ψ(1)=ψ(2)=ψ(3)=0
这样的封闭方式, 恰好能与等式右端具有2阶碰撞精度的q(κ)保持一致。虽然Eu与Myong对高阶矩的封闭方法有各自不同的看法, 但是基于两种封闭理论的简化效果是一致的, 即不考虑高阶矩在演化方程中的作用。
(2)绝热假设

其实NCCR方程的表达形式与N-S方程既有联系, 又有区别。一方面该方程组保留了N-S本构方程中的线性部分, 另一方面也有其特有的非线性效应。首先, 在NCCR方程中的应力Π和附加体积应力Δ与速度的各梯度分量, 不再是线性关系。同样地, 热流Q与温度梯度也不再线性相关。另外, 非线性耗散项q(κ)的引入不仅增强了方程组的非线性程度, 同时又将非守恒变量耦合在一起。然而, 在传统的N-S方程中, 可以很明显地发现, 应力和热流不是直接相关的变量。为了便于对比, 将N-S方程的本构模型, 罗列如下
1.4 NCCR方程的无量纲化与归一化
为了更好地实现NCCR方程的理论求解, 在实际的应用过程中通常采用如下的无量纲体系对控制方程与非线性耦合本构模型进行无量纲化处理[37-39]
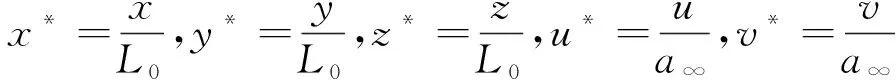
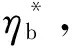
其中,
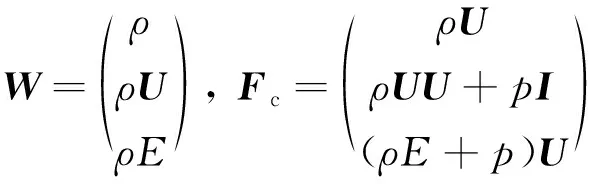
与此同时, 为了将NCCR方程写成极简练的形式, 引入如下归一化方式

最终, 可以将归一化处理后的NCCR方程写成
2 非线性耦合本构关系求解方法
NCCR模型尽管在GHE方程基础上得到很大的简化, 但是由于高阶非守恒量的强非线性与强耦合性特征, 难以对其直接进行数值求解。NCCR目前的求解方法主要有两种, 解耦求解方法与耦合求解方法。
2.1 解耦求解方法
Myong提出的NCCR模型的非线性代数方程组解耦求解方法[21-22], 实则将一个耦合系统分裂为单一方向的解耦系统。并在此基础上对每个方向独立求解, 最终通过简单线性迭代的方式给出NCCR方程的收敛解。Myong的解耦算法[40]将三维问题近似分裂为x,y,z这3个方向的一维问题来处理。在三维有限控制体的一个面上(如x面), 由热力学力(ux,vx,wx,Tx)引起的应力和热流分量(Πxx,Πxy,Πxz,Δ,Qx), 可以近似成两个分裂求解器的线性叠加。其中一个求解器求解压缩膨胀流动(ux,0,0,Tx), 另一个计算剪切流动(0,vx,0,0)和(0,0,wx,0)。
2.2 耦合求解方法
NCCR模型的解耦求解算法虽然在一维激波结构和二维简单外形问题上初步展示它的能力。然而, 这种分裂思想忽略真实流动中3个方向的相互影响, 弱化了本构关系中非守恒量之间固有的耦合关系。因此, 本节重点阐述如何通过一种耦合思想完整地求解非线性耦合本构关系模型。首先, 在剪切应力无迹和对称关系条件下, 应力满足如下关系
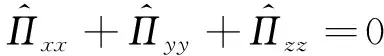
因此, 适用于双原子气体分子的NCCR本构方程可表达成如下非线性方程组的一般形式
式中, 每个函数fi可以看作是将一个九维实数空间里的自变量映射到一维实数空间的关系。若将含有9个未知量的9个非线性方程表示成一个矢量函数形式, 则
那么, 双原子NCCR模型的一般形式可简化为
F(x)=0
(4)
(1)不动点迭代法
对于双原子NCCR本构关系模型, 首先尝试采用不动点迭代法进行求解和分析。非线性方程组的一般形式(4)可改写成等价的不动点形式[23]为
x=G(x)
虽然不动点迭代收敛速度只有1阶, 甚至越接近解的区域迭代收敛速度越慢, 但其对迭代初值依赖性不大。因此, 不需要给出一个充分接近解的初值。不动点迭代最大的难点在于如何构造一个满足不动点迭代收敛定理的多变量显式迭代式。所以, 在构建不动点迭代式之前, 首先将无量纲归一化处理后的双原子NCCR模型转换成如下形式
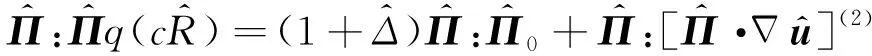
考虑到以上方程形式依然复杂, 可在Rayleigh-Onsager耗散函数形式的基础上将上式合并成一个表达式
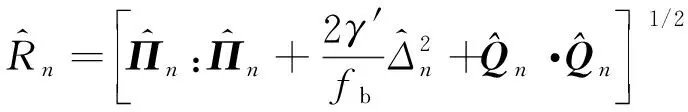
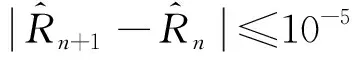

图1 不动点迭代法收敛情况[23] Fig. 1 Convergence of fixed-point iteration method[23]
(2)Newton迭代法
由不动点迭代收敛性分析可知, 给双原子NCCR模型构造一个在所有范围均能完全收敛的不动点迭代式是比较困难的。因此, 继续尝试采用另一种求解算法——Newton迭代法。首先, 将NCCR模型转换成另一种更广义的形式[23]
G(x)=x-A(x)-1·F(x)
其中,A(x)是从九维实空间映射到一维实空间的函数矩阵, 在G的不动点p处非奇异。在非线性方程组的Newton迭代法中,A(x)的一个合适形式是Jacobi矩阵J(x)。从x(0)初值开始, 迭代过程不断演化推进求解。对于k≥1, 有如下关系式
x(k)=G(x(k-1))
是的,李莉现在觉得很幸福,是那种能摸得着地的幸福。梅子说的许峰,是她记忆深处的人,如若不提,她几乎忘记他了。
=x(k-1)-J(x(k-1))-1F(x(k-1))
(5)
虽然, Newton迭代法一般具有二次收敛速度, 但是过度依赖于一个充分准确的初值, 而且Jacobi矩阵必须存在。此外, 式中的迭代需要在每一步计算Jacobi矩阵的逆矩阵, 这样会存在计算量巨大和计算复杂性增加的缺陷。为了避免对Jacobi矩阵直接求逆, 式(5)的计算过程通过两步方式代替实现。首先采用Gauss消去法求解线性方程组, 以获得每一步的迭代增量Δx
J(x(k-1))Δx=-F(x(k-1))
然后, 在旧时刻的迭代值x(k-1)基础上, 通过迭代增量Δx以获得新的近似解x(k), 如
x(k)=x(k-1)+Δx
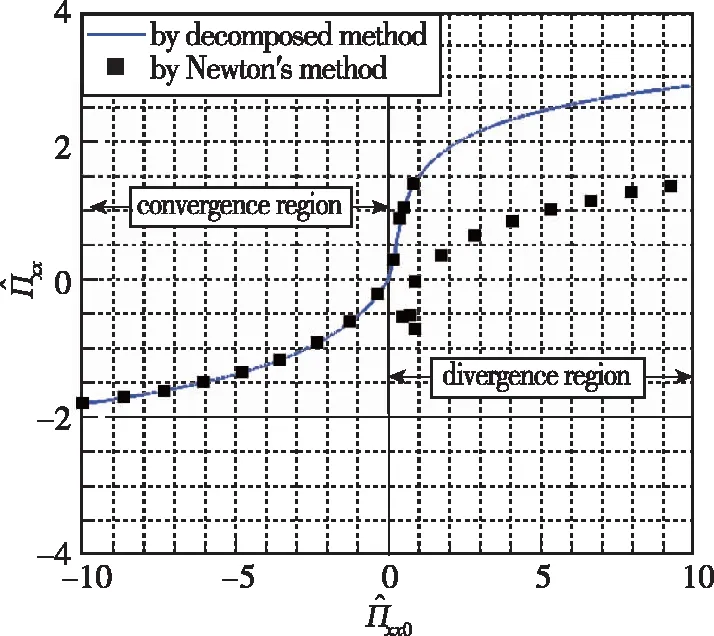
图2 Newton迭代法收敛情况[23]Fig. 2 Convergence of Newton′s iteration method[23]
(3)混合迭代法

图3 混合迭代算法收敛情况[23]Fig. 3 Convergence of hybrid iteration method[23]
3 NCCR数值求解与验证
3.1 一维激波结构
一维激波结构是验证气体数值模型精度的经典流动算例。其不仅能够表征高Mach数流动中的热力学非平衡特点, 同时能够将边值问题转变为初值问题, 从而避免了边界条件的处理。因此, 对于NCCR方程的研究首先从一维激波结构[25]的模拟出发。
图4展示了通过NCCR方程求解氩气激波结构的无量纲密度厚度倒数结果。从图中的对比结果可以发现, 采用VHS模型且取黏性指数s=0.81, 能够使得NCCR的解与实验结果吻合最好。然而, 采用Sutherland黏性的NCCR方程预测的结果与实验值相比有一定差距。图5详细对比了NCCR方程求解双原子气体得到的无量纲密度厚度倒数与实验结果。由密度厚度倒数曲线可见, 传统NSF方程在不考虑体积黏性情况下预测结果最差。然而, NCCR方程在大Mach数范围内与实验测量值吻合最好。同时, 也可以发现, 不管是NSF方程还是NCCR方程, 体积黏性均有助于提高对双原子气体流动的预测精度。
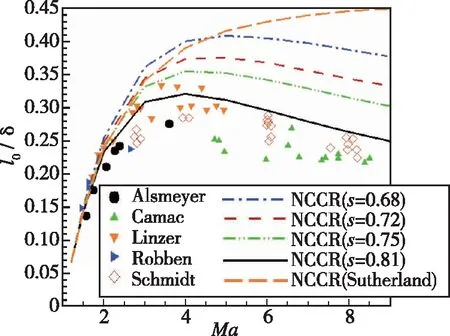
图4 氩气激波结构的无量纲密度厚度[25]Fig. 4 Comparison of dimensionless density thickness of Argon shock structure[25]
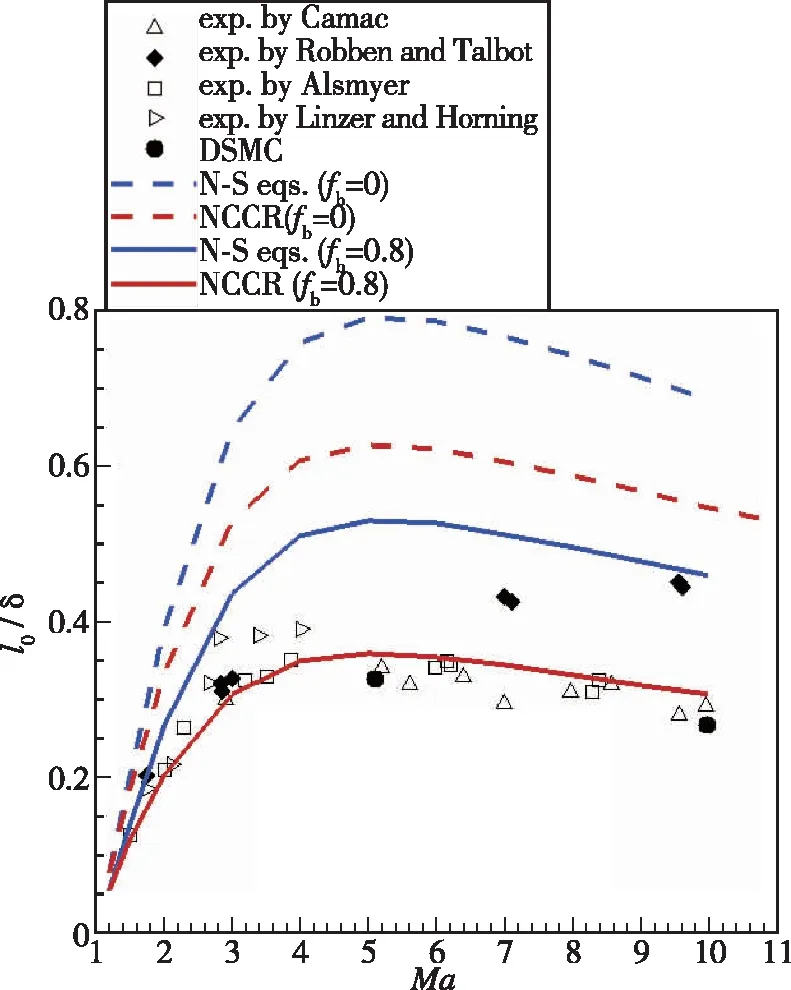
图5 氮气激波结构的无量纲密度厚度[25]Fig. 5 Comparison of dimensionless density thickness of Nitrogen shock structure[25]
3.2 二维圆柱绕流
为进一步验证NCCR方程的模拟精度, 在有限体积计算框架下实现了NCCR方程对简单二维外形的求解。图6展示了NCCR方程模拟的高超声速圆柱绕流无量纲速度云图。图7展示了由解耦算法与耦合算法预测的NCCR速度曲线与DSMC的对比结果。不难发现, NCCR方程采用耦合算法预测的结果与DSMC在激波处十分吻合。然而, NCCR的解耦算法预测的结果与DSMC有较为明显的偏差。这也意味着解耦算法忽略掉NCCR模型的重要流动特征信息的确会降低方程的模拟精度。因此, 耦合收敛算法对NCCR模型求解的稳定性和精度有着非常重要的影响。
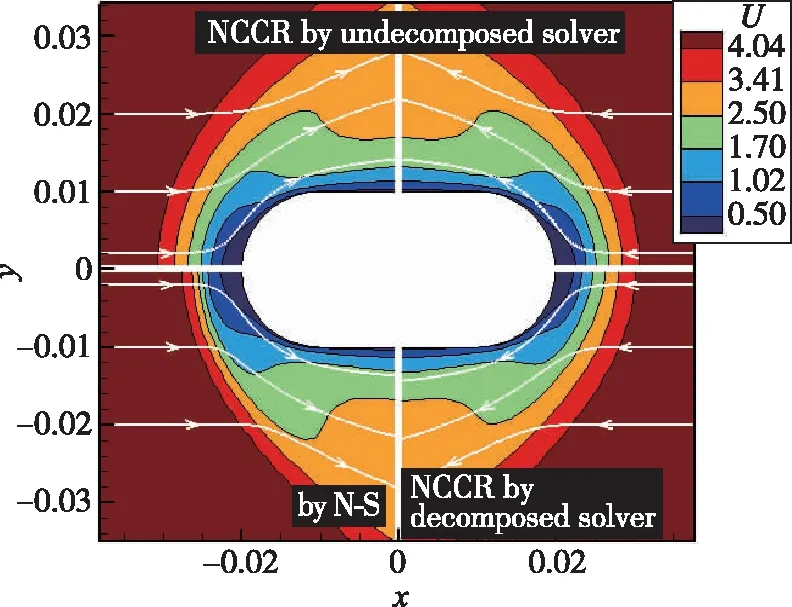
图6 氮气圆柱绕流速度云图[23]Fig. 6 Comparison of velocity contours for Nitrogen gas[23]
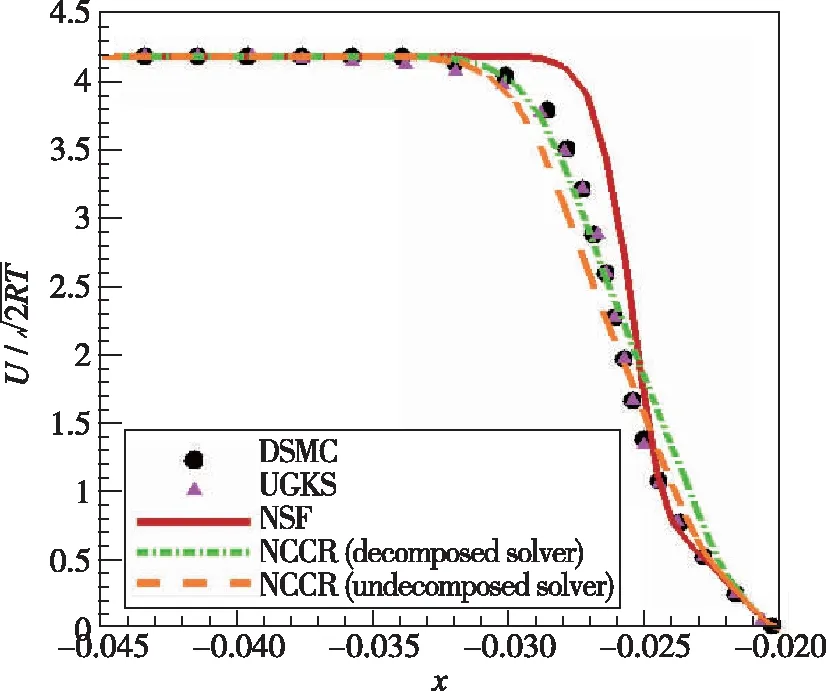
图7 驻点线速度分布[23]Fig. 7 Comparison of velocity profiles along stagnation line[23]
3.3 类HTV-2飞行器
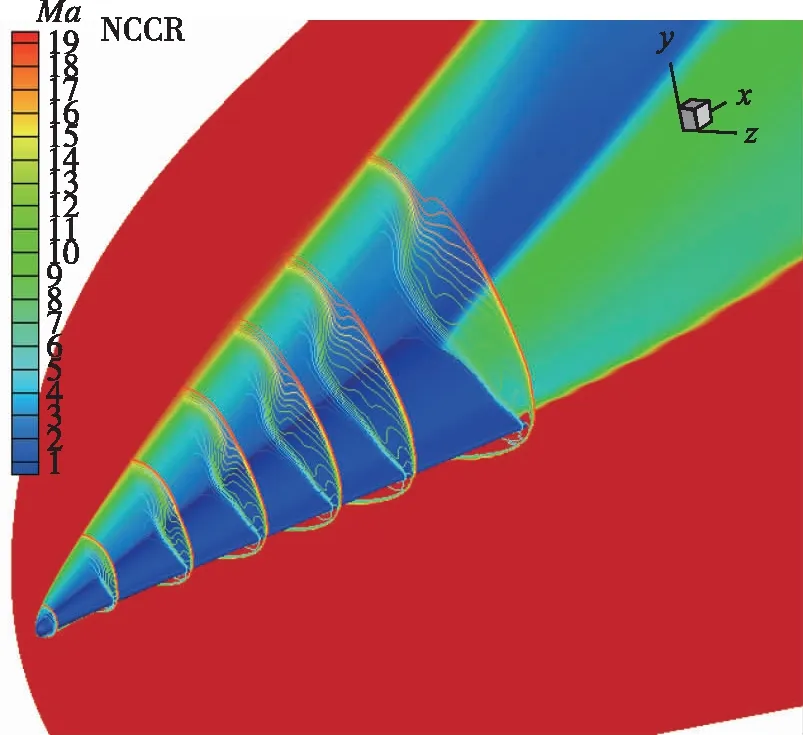
图8 Mach数云图(H=50 km)[26]Fig. 8 Mach number contours(H=50 km)[26]
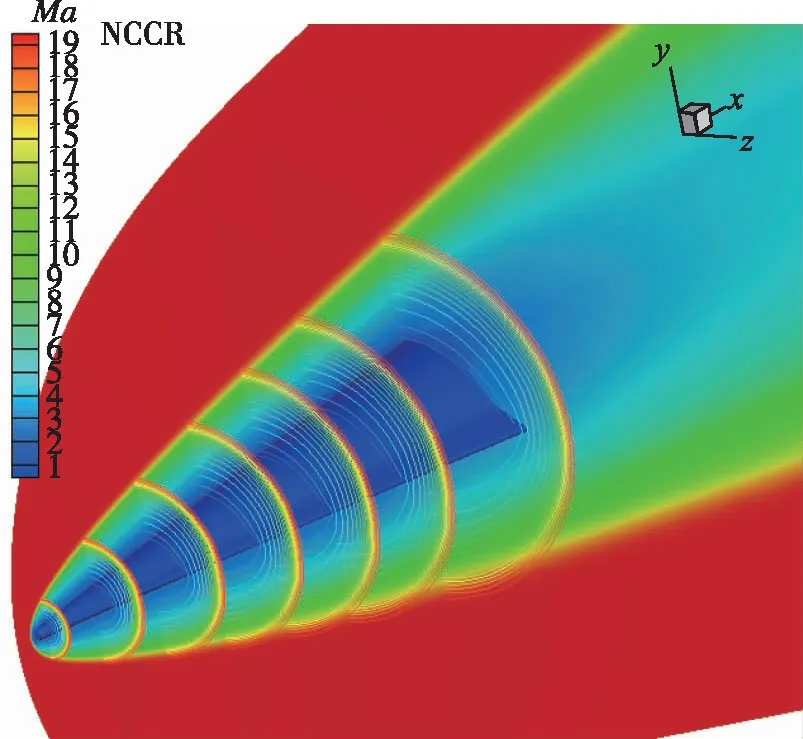
图9 Mach数云图(H=90 km)[26]Fig. 9 Mach number contours(H=90 km)[26]
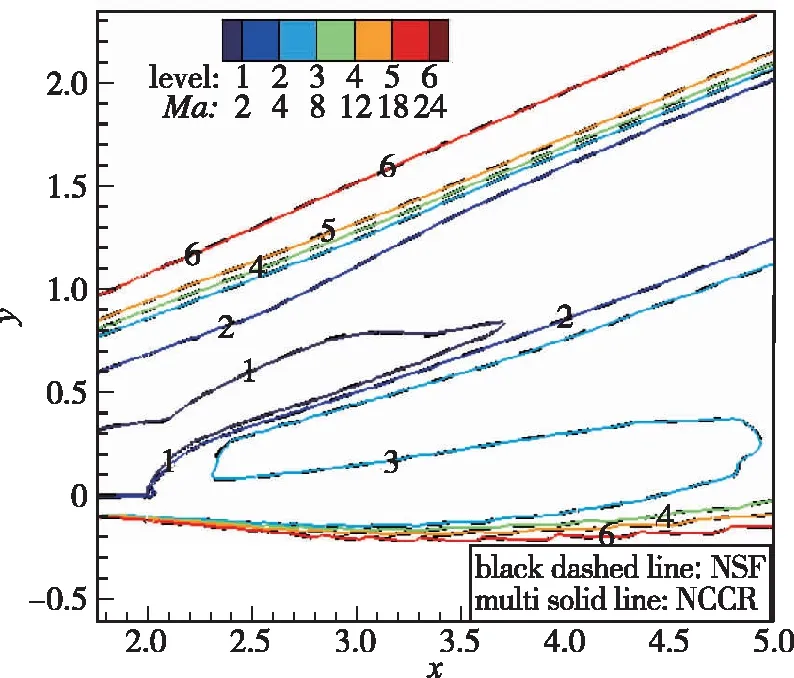
图10 背风区Mach数云图对比(H=50 km)[26]Fig. 10 Contour lines of Mach number of after-body flows(H=50 km)[26]
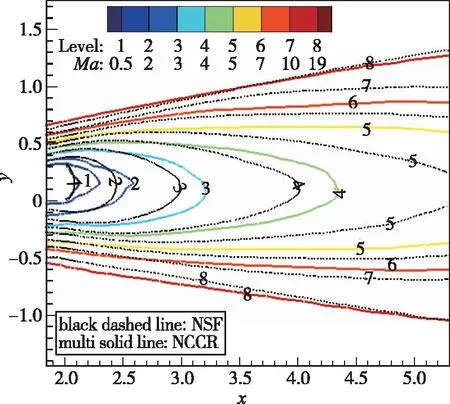
图11 背风区温度云图对比(H=90 km)[26]Fig. 11 Contour lines of Mach number of after-body flows(H=90 km)[26]
因此, 可以看出在连续流区域, NCCR方程的模拟结构能够恢复到N-S方程的结果。在N-S方程失效的非平衡区域, NCCR方程能够体现出其差异性。
4 改进模型NCCR+

(6)
若对方程(6)进行无量纲化与归一化处理, 可以将其表达形式写为
为了验证NCCR+方程的模拟精度, 基于高超声速扩张拐角的内流场, 进行了详细的对比分析。从图 12的对比结果可以明显地发现, 在扩张区域采用DSMC预测所得的温度场与基于NCCR+模拟的数值结果吻合较好。为了进行定量的分析研究, 截取x=0.15 mm温度曲线, 并将NCCR+的预测结果与N-S, NCCR 和DSMC一同对比分析。从图13的对比结果中均可以发现, 扩张区域由于强烈的稀薄气体非平衡效应, N-S求解器的数值计算结果与DSMC相差甚远。而采用NCCR+方程预测所得的温度曲线与DSMC的结果吻合得很好。而采用传统NCCR方程预测所得的结果也与DSMC方法的模拟值比较接近。从以上分析结果中可以看到, NCCR+方程对于非平衡扩张区域的模拟具有潜在的优势。同时也可以发现在传统NCCR方法计算过程中, 对热流本构关系的简化处理确实在一定程度会降低模型的计算精度。
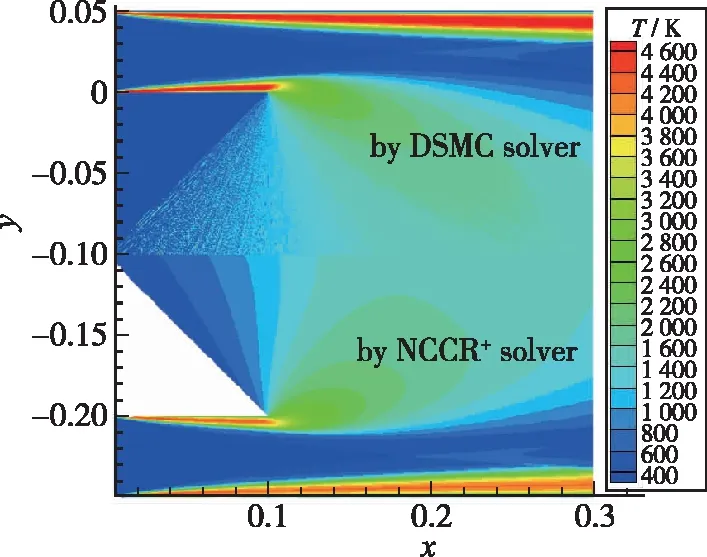
图12 DSMC和NCCR+温度云图对比[33]Fig. 12 Comparison of temperature contours between DSMC and NCCR+[33]
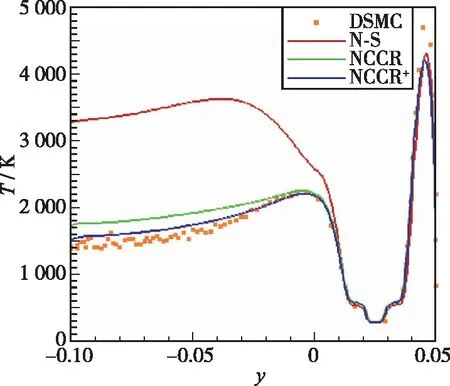
图13 截面处温度曲线对比[33]Fig. 13 Comparison of temperature profiles[33]
为了验证采用NCCR+方法, 模拟三维工程外形的能力, 分别对95 km和105 km的Apollo返回舱再入过程进行了数值模拟与对比。从图 14和15中的压力对比云图可以明显发现, 采用NCCR+预测得到的激波脱体距离明显大于N-S方程, 更能体现出稀薄气体非平衡效应。
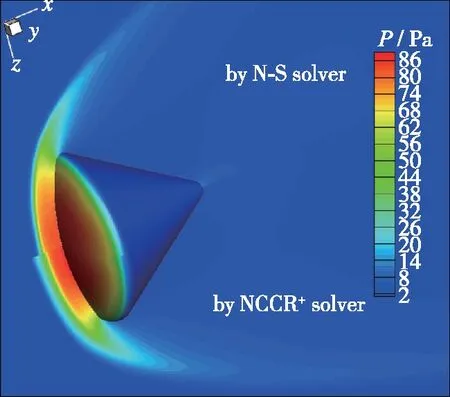
图14 压力云图对比(H=95 km)[33]Fig. 14 Comparison of pressure contours (H=95 km)[33]
从图 16和17物面摩阻系数对比曲线可以发现, 在95 km与105 km高度, 基于NCCR+方程模拟得到的摩阻系数在迎风区与背风区均与DSMC结果吻合较好。而基于传统N-S方程模拟得到的摩阻系数在背风区结果明显高于DSMC的预测值。同时在迎风区, NCCR+预测所得的热流曲线比NCCR更接近于DSMC的预测结果。

图17 物面摩阻系数对比(H=105 km)[33]Fig. 17 Comparison of surface friction coefficient(H=105 km)[33]
5 NCCR方程耦合转动非平衡效应
针对高超声速气体而言, 气体的压缩膨胀效应十分显著, 体积黏性表征了气体的压缩膨胀效应。因此, 对于体积黏性的研究也尤为必要。通常为了更好地描述体积黏性, 引入黏性系数比, 即体积黏性系数与剪切黏性系数的比值, 其表达形式如下
针对不同种类的气体, 由于气体属性不同,fb的取值其实也不相同。Prangsma等[42]利用声波吸收实验在77 K下测得氖气的ηb=0, 从实验层面证明了单原子气体体积黏性等于零的理论预测。同时, 在温度为293 K的测试环境下, 分别测量出了N2, CO, CH4和 CD4, 它们的fb值分别为 0.73, 0.55, 1.33 和1.17。这也表明在常温下, 这些气体的体积黏性系数与剪切黏性系数基本在同一量级。在之前NCCR方程的研究中, 针对双原子N2而言,fb的值统一近似取为0.8。为了给NCCR方程提供双原子氮气fb更加精确的取值方式, 通过连续性理论和分子动理学理论给出了fb的取值的精确表达形式, 具体如下
当f(γ)等于γ-1时表示由动理学理论得到的相应系数, 当其等于γ时表示由连续介质理论得到的相应系数。上式中Zrot表示转动碰撞数, 其具体表达式如下
如图18所示, 在300 K左右, 相比于连续介质理论下的体积黏性系数, 基于动理学理论得到的黏性系数比fb与实验结果更加吻合。同时, 在图中也可以看到, 氮气分子体积黏性系数与剪切黏性系数的比值随着温度的升高而逐渐增大。在600 K左右时, 近似等于0.8, 这也给出了传统NCCR理论在高超声速建模过程中黏性系数比取值为0.8的合理性区间。
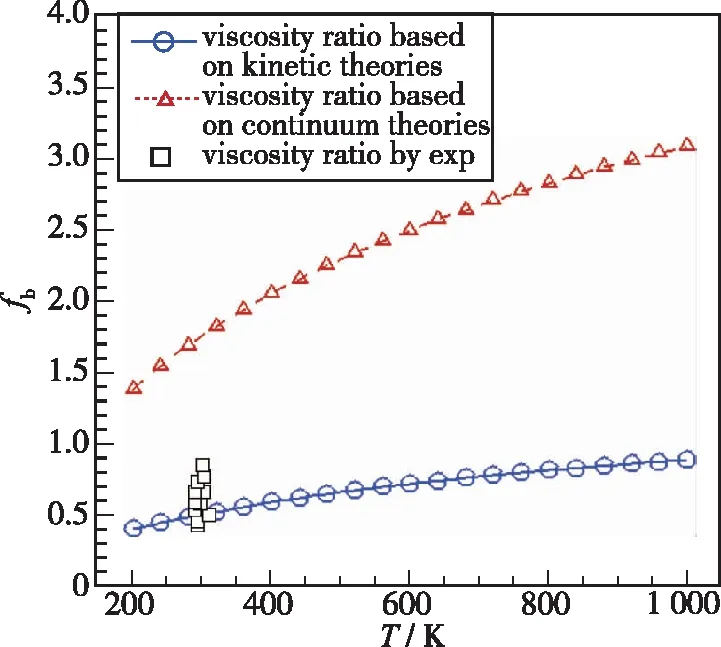
图18 黏性系数比[34]Fig. 18 Viscosity ratio[34]
双原子气体除了体积黏性效应, 在高Mach数流动问题中, 由于转动温度向平动温度松弛过程的相对弛豫时间往往较长, 因此转动非平衡的效应尤为明显。为了更好地描述高超稀薄环境下的转动非平衡流动过程, 在NCCR方程的基础上加入了转动能松弛源项,最终实现了可以考虑双温度非平衡效应的NCCR模型[34]。
图19比较了带转动能松弛源项的N-S方程和NCCR方程计算所得的Mach数云图。从图中可以看到, 在滑移流区, 即Kn=0.05, 两者略有差异; 当Kn=0.25到达过渡流区, 流场非平衡程度显著, 采用NCCR方法预测的激波脱体距离明显大于N-S方程预测的结果, 其对非平衡效应的捕捉能力更为突出。
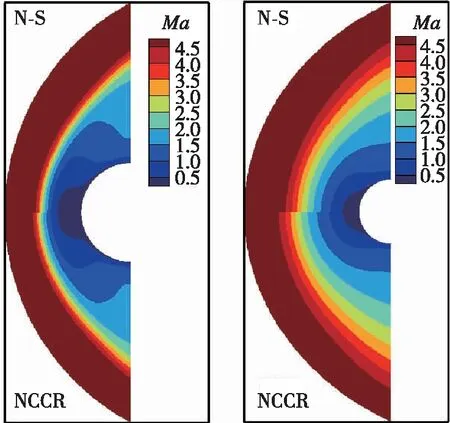
(a) Kn=0.05 (b) Kn=0.25图19 Mach数对比云图[34]Fig. 19 Comparison of Mach number contours[34]
如图 20所示, 在Kn=0.05的滑移流区, NCCR与N-S方程预测驻点线温度曲线差异明显。相比于N-S方程预测的结果, NCCR方程预测的激波层耗散性更强, 并且在平动和转动温度分布上均与DSMC模型更吻合。
激波与激波边界层相互作用[41]是高超声速航天器绕流问题中一个常见的现象。高超声速尖壁前缘附近的激波与边界层相互作用, 会对平动能与转动能的交换产生强烈的非平衡效应。本算例采用NCCR的双温度模型模拟了高超声速平板绕流, 并与文献[43]中Tsuboi等的实验测量结果和DSMC的数值模拟结果进行了比较。如图 21所示, 在研究过程中采用含双温模型的NCCR方程, 给出了平板周围的转动温度Trot。
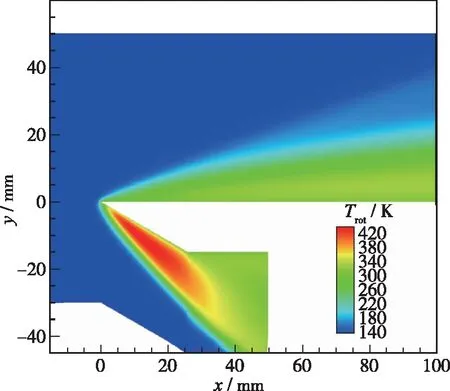
图21 转动温度云图[34]Fig. 21 Rotational temperature contours[34]
图22展示了采用双温度NCCR计算的平动和转动温度与DSMC和实验数据[39]对比结果。从对比图中可以看到, 双温度NCCR方程的计算结果与实验测量值吻合很好, 甚至在某些区域比DSMC方法更接近于实验测量结果。
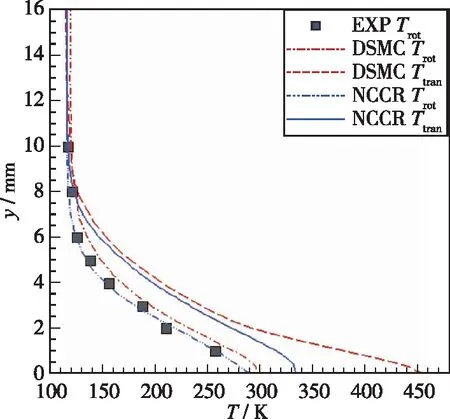
图22 截面处温度曲线对比[34]Fig. 22 Comparison of temperature profiles[34]
6 NCCR与热化学非平衡的耦合计算
目前, 直接模拟Monte Carlo方法(direct simula-tion Monte Carlo, DSMC)[44]是唯一能够用于模拟过渡流化学反应的有效方法。但现有DSMC方法对于近连续热化学非平衡流条件下的流动求解仍不能同时具备高效、 工程可用的特点[45]。因此, 本节主要论述NCCR方程与化学反应动力学的耦合计算模型[35,46]。其中, 化学反应模型主要采用Gupta 7组元化学反应动力学模型[47], 包括5种中性空气组分N2, O2, N, O和NO以及两种带电粒子e-和NO+。
图 23对比了81 km高度采用NCCR与N-S方程计算所得的温度云图。可以看到, 在考虑真实气体效应情况下, N-S方程和NCCR方程预测的结果差别较大, 尤其是激波脱体距离。
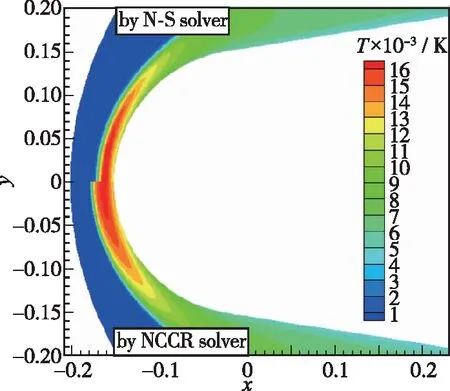
图23 N-S与NCCR温度云图对比(81 km)[35]Fig. 23 Comparison of temperature contours between N-S and NCCR (81 km)[35]
除此之外, 将基于理想气体的NCCR方程与基于真实气体效应的NCCR方程的计算结果进行了对比分析。图 24和25分别比较了71 km和 81 km 高度下对称面温度分布云图。从对比云图中可以发现, 在考虑真实气体效应的情况下, 预测的激波脱体距离明显小于理想气体模型预测的结果。因为在真实气体效应的影响下, 由于化学产物的生成, 钝锥前缘的等效密度升高。因此, 稀薄非平衡效应减弱, 激波脱体距离变小。这一现象是符合物理规律的。同时, 可以明显地发现, 在考虑真实气体效应的情况下预测的流场温度远远低于理想气体效应下的预测结果, 这一现象也是符合物理规律的。

图24 理想气体与真实气体效应下温分布云图对比(H=71 km)[35]Fig. 24 Comparison of temperature contours between perfect gas effect and real gas effect(H=71 km)[35]

图25 理想气体与真实气体效应下温分布云图对比(H=81 km)[35]Fig. 25 Comparison of temperature contours between perfect gas effect and real gas effect (H=81 km)[35]
7 总结与展望
本文主要从理论研究与工程应用两个方面综述回顾了NCCR方程的发展历程。在理论研究方面, 主要分析了耦合无分裂算法求解NCCR方程的有效性与必要性。该耦合方法结合了不动点迭代和Newton迭代的各自优势, 弥补了Myong分裂思路对NCCR方程流动的缺陷。基于该方法, 成功地将NCCR方程的求解从一维拓展至三维流动, 为推向工程应用提供了坚实的基础。为了进一步提高NCCR方程的求解精度, 提出了改进的NCCR+方法, 并通过高超声速扩张拐角流动与Apollo返回舱的再入流场, 验证NCCR+的确具有更有效的稀薄非平衡效应捕捉能力。为了更加符合高超声速流动热力学与热化学非平衡的特性, 提出了基于非线性耦合本构关系的多温度模型, 以及考虑化学反应源项的NCCR方程, 并用于探究稀薄气体效应与真实气体效应耦合作用下的流动机理。虽然NCCR方程的研究取得了一定进展, 但仍有很大的发展空间, 将对其进行不断深入的研究, 进一步拓展NCCR方程的应用范围。
