微通道内气体流动的DSMC方法

张文雯， 王学德

(南京理工大学能源与动力工程学院， 江苏南京 210094)

引 言

随着微机电系统以及纳米技术的飞速发展， 各式各样的微机械设备与元件已应用于自动控制、 医疗仪器、 电子冷却和航空航天等诸多领域中[1-4]， 其中涉及了许多有关微通道的流体流动， 使得微通道内部气体的流动特性受到研究人员的广泛关注。近年来， 研究人员基于不同形状的直微通道气体流动做了很多工作[5-7]， 而在微通道的实际应用中普遍存在着内部流道横截面变化的复杂情况， 关于此类情况的相关研究较少。孔口模型作为微机电系统中典型的流道截面变化结构， 其流道截面出现收缩/扩张现象， 导致流场产生压降并伴随流动分离现象[8]。因此， 揭示气体在具有孔口结构微通道下的流动机理对于微机电系统实际装置的设计、 制造和运行具有重要的意义。

本文采用直接模拟Monte Carlo(direct simul-ation Monte Carlo， DSMC)方法对微尺度气体流动进行模拟， 网格尺寸和时间步长等模拟参数会直接影响DSMC模拟结果的准确性。在以往的微流体研究中， 网格尺寸与时间步长研究较少， 国内外研究人员通常做法是以Bird[9]提出的网格最大尺寸约为当地分子平均自由程的1/3作为划分依据。但微通道流动平均自由程较小， 根据此原则会导致网格数量过多以及模拟分子数急剧增加， 造成极大的运算成本。

因此， 为解决以上问题， 本文首先针对压力梯度驱动的微通道流动发展了基于压力边界条件的DSMC方法。随后定义CSL数和DCFL数两个无量纲参数作为网格尺寸和时间步长的约束条件， 通过对微通道流的模拟， 总结了在DSMC方法中微尺度条件下网格尺寸和时间步长的一般选取原则。并在该选取原则的基础上， 探究了单/双孔口结构微通道内气体流动结构， 并通过改变入口压力分析流道截面变化对气体流动的影响。

1 微通道DSMC压力边界条件

微通道中的气体流动往往是由压力梯度驱动的低速流动， 此时， 分子数密度、 来流速度等参数难以获得， 压力和温度是边界上唯一已知的物理量[10]， 因此， 采用DSMC压力边界条件。已知进口压力pin, 温度Tin以及出口压力pe, 流入或流出微通道的粒子数通量为

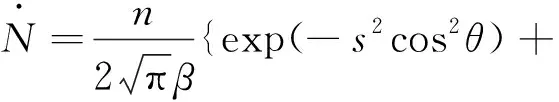
(1)

式中，n表示分子数密度，θ为速度方向与边界法向的夹角， erf表示的是误差函数，s为分子速率比，β表示分子最可几速度cmp的倒数， 即

式中，T和u分别表示边界温度以及来流平均速度分量,m为分子质量，k为Boltzmann常数。

采用基于特征理论的压力边界条件[11]进行计算。对于进出口边界单元(in表示入口边界， e表示出口边界)， 每个单元j的宏观速度u, 出口密度ρe以及出口温度Te由下式与式(1)迭代求解

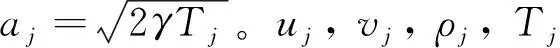
ρj=njm，pj=njkTj

Tj=(3Ttr+ζTrot)/(3+ζ)

式中，Nj为网格内的采样粒子数，Ttr为平动温度，Trot为转动温度，ζ为转动自由度。

2 微通道DSMC方法验证

采用经典微Poiseuille流验证微尺度DSMC方法的有效性。二维微通道几何模型如图 1所示， 计算条件取自文献[12]， 见表 1。其中，H为 0.4 μm，L为2 μm。左右边界为自由来流， 模拟氮气在微通道内流动特性， 上下边界为采用漫反射模型的固体壁面。无时间计时器技术(no time counter， NTC)和可变硬球(variable hard sphere， VHS)模型被用来模拟粒子之间的碰撞。

图1 微通道基本结构Fig. 1 Basic structure of the microchannel

表1 微通道计算参数Table 1 Numerical parameters for microchannel

图2给出了两种压力比的中心线压力分布与壁面滑移速度us变化的比较结果。图2(a)首先将本文使用特征压力边界条件的DSMC计算结果与Arkilic等[13]通过1阶解析压力分布作比较， 结果表明本文计算结果与解析解具有较高的一致性， 验证了本文程序的准确性。同时将压力与壁面滑移速度与Fang[12]使用隐式边界条件的结果进行对比， 两种分布量的模拟结果均符合较好， 进一步证明本文方法的有效性。

(a) Centerline pressure distribution

(b) Wall slip velocity distribution图2 微通道模拟值与文献值的对比Fig. 2 Comparison between simulation and reference results

3 网格尺寸与时间步长约束条件

DSMC方法的本质是在一段时间步长Δt内， 使得分子运动和碰撞能够解耦。但为了确保能达到正确解耦的目的， 一般需要保证以下两个条件[14]: (1) 网格尺寸小于分子平均自由程λ, 一般取为平均自由程的1/3； (2) 时间步长Δt小于平均碰撞时间τ。下面研究其在微通道内的适用性和可扩展性。为此， 首先定义一个无量纲参数CSL表示网格尺寸与平均自由程之间的关系。同时借用计算流体力学中CFL数来定义一个新的参数DCFL数限制时间步长， 表示如下

以压力比为2.5的微通道来验证网格尺寸和时间步长对计算结果的影响。计算了6种不同CSL数和DCFL数组合工况， 如表 2所示。其中， 工况3为第2节验证算例中压力比为2.5的计算参数， 以该参数下的计算结果作为比较的基准。由表中数据可知， 除了工况6的DCFL数等于1外， 其余情况DCFL数均小于1。

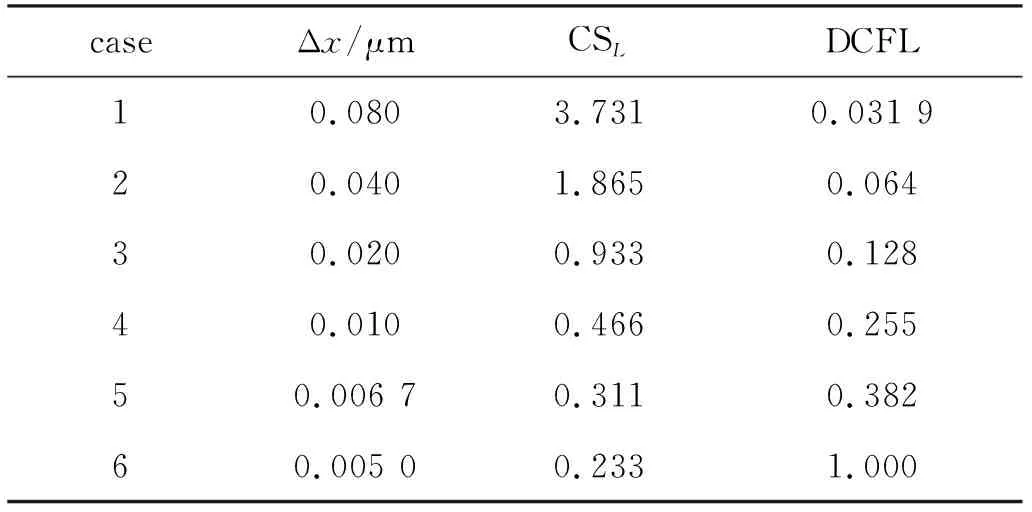
表2 网格尺寸与时间步长约束参数Table 2 Constraint parameters for grid size and time step

图3给出了各种工况下中心线压力分布与解析压力值对比情况， 可以看出除了工况6之外， 其余工况的压力分布均与解析值符合良好。为了进一步分析时间步长与网格参数对其他物理量的影响， 图 4， 5分别给出了中心截面处速度分布与沿通道中心线温度分布， 可以看出DCFL数小于1的工况1， 2， 4， 5的速度与温度分布结果与经过验证的工况3的结果趋于一致， 在工况6情况下， 中心截面速度与温度的计算结果误差均出现较大的偏离。综合比较图3， 4， 5的计算结果， 可以得到在选取网格尺寸和时间步长时， 首先应当保证DCFL数的取值小于1作为时间步长的约束条件。

图3 中心线压力分布对比Fig. 3 Comparison of centerline pressure distribution

在满足DCFL数小于1的情况下， 进一步分析CSL数对中心截面速度与温度计算结果的影响。从图 4看出工况1中心截面的流向速度明显偏小， 而工况2， 4和5均能得到与工况工况3较为一致的模拟结果， 从而表明在CSL数小于1.865时也可以得到较为准确的计算结果。从图 5(b)的局部放大图中可以看出工况5的中心线温度较工况 3 明显偏低。由此可见， 在选择网格尺寸时不需要过分追求小CSL数， 当网格尺寸很小时， 是同一个网格内模拟分子碰撞的次数减少， 造成一定统计误差， 并且由于网格数量变多， 流场收敛需要的时间变长， 增加了运算成本。因此， 在确保DCFL数小于1的前提下， 选择CSL数接近于1可作为本文网格尺寸选取的原则。

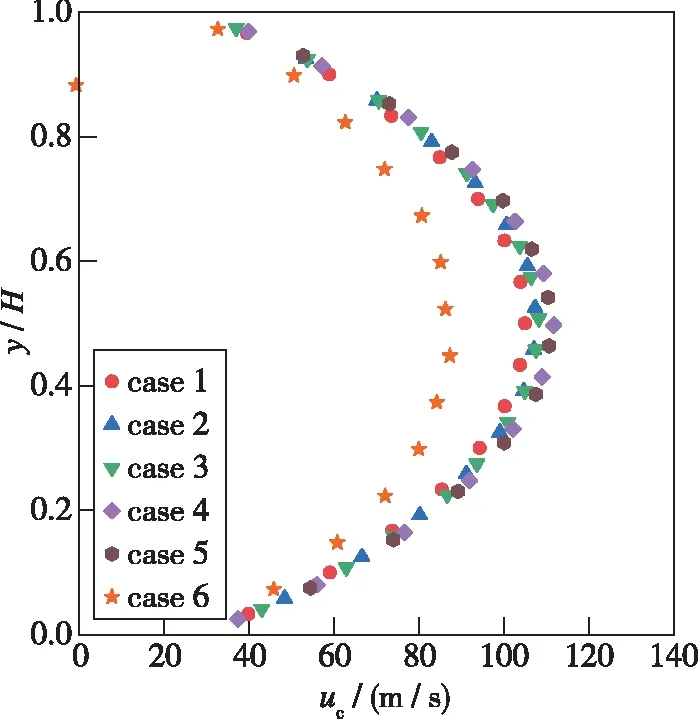
图4 中心截面处流向速度分布对比Fig. 4 Comparison of velocity distribution at the channel midspan

(a) Centerline temperature distribution

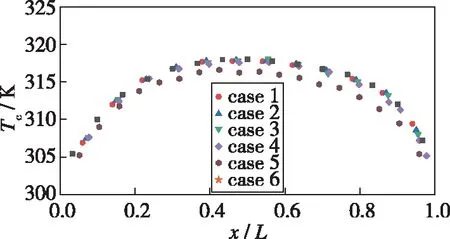
(b) Enlarged red frame图5 中心线温度分布对比Fig. 5 Comparison of centerline temperature distribution

4 单/双孔口微通道流动特性研究

4.1 几何条件设置与物理模型

研究模型为具有单/双孔口结构的微通道， 如图 6所示， 两种不同孔口结构的尺寸参数见表 3， 壁面采用漫反射模型， 模拟气体为氮气， 不同入口压力条件下[9]的来流条件见表 4， 进出口流态均处于滑移流状态。

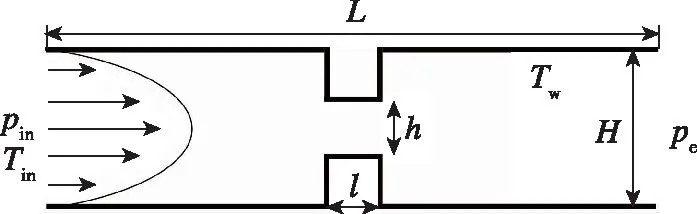
(a) Single orifice model

(b) Double orifice model图6 微通道几何形状示意图Fig. 6 Schematic of the microchannel geometry

表3 不同形状模型的几何条件Table 3 Geometric conditions of different shapes

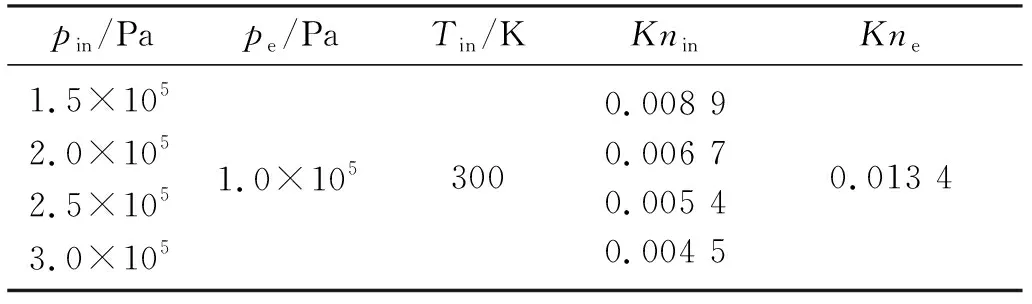
表4 孔口流通道参数Table 4 Orifice flow channel parameters

4.2 入口压力对微通道流场的影响

图 7分别给出了不同入口压力下， 单/双孔口模型通道内的流线与压力等值线分布图。在单孔口模型中， 通道上游处流线沿拐角进入孔， 在孔口内部流线与通道平行， 主流经孔口加速， 在孔口出口形成一股收缩流， 由于管道突然扩张， 流动减速以充满整个通道。孔口出口由于流动速度降低， 压力对应升高， 在孔口下游的拐角处形成反向压力梯度， 从而出现回流区。在双孔口模型中， 具有与单孔口模型相似的流动结构， 且每一个孔口后均存在回流区。此外， 当入口压力增大之后， 由于出口压力始终保持不变， 逆压区的压差增大， 回流区尺寸随之变大。在双孔口模型中， 重点关注两孔口之间的过渡区域， 入口压力为1.5×105Pa时， 在过渡区拐角处出现了两处分离， 孔口2的上游也出现一个很小的分离区。这是由于流体在过渡区流程较短， 流体经过孔口压缩加速， 无法及时调整流向， 出现分离区。而随着入口压力的增加， 分离区的尺寸增大， 两处分离逐渐融合， 形成一个大的分离涡。

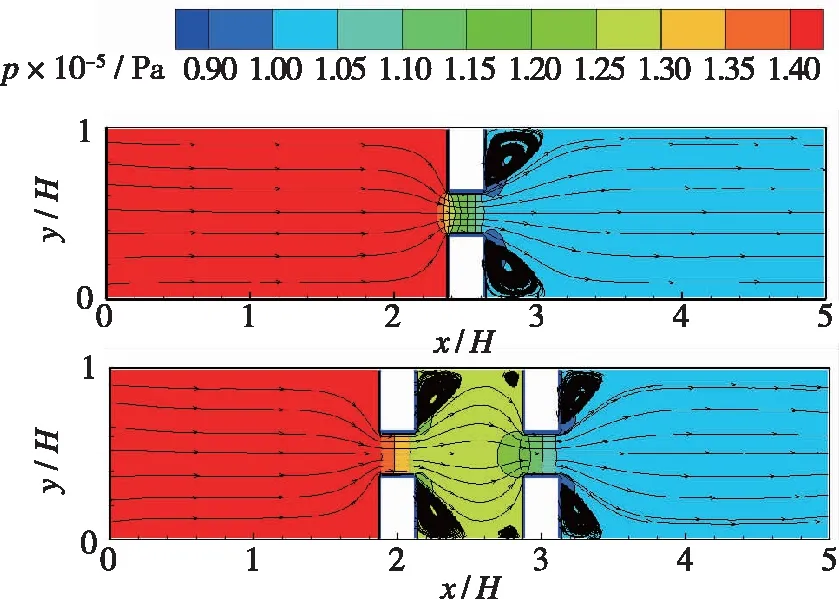
(a) pin=1.5×105 Pa

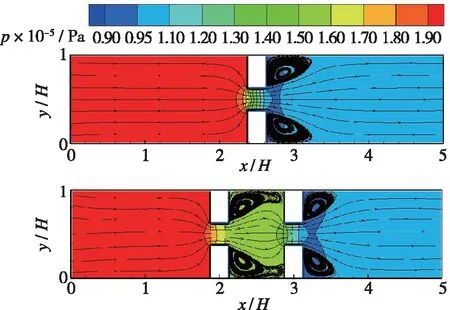
(b) pin=2.0×105 Pa

(c) pin=2.5×105 Pa

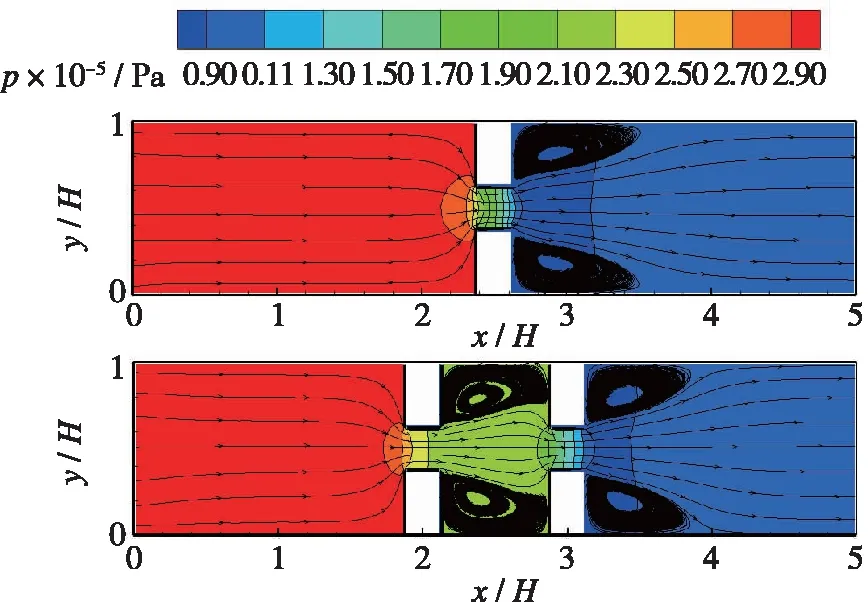
(d) pin=3.0×105 Pa图7 流线与压力等值线云图Fig. 7 Streamlines and pressure contours

图8给出了单/双孔口的中心线压力分布曲线， 从中可以看出主要的压力变化均集中于孔口位置， 两种模型均在孔口位置出现了较大的压降， 其中， 双孔口模型经历了两次压降， 第2次压降比第1次大很多。这是由于当流道收缩使得流体加速时， 流体的静压能转换为动能， 孔口上游的压力快速下降。此外， 最小压力不是在截面最小的孔口处， 而是出现在孔口下游， 随着入口压力的增大， 最小压力的位置也随之后移， 并且孔口后的压力甚至会小于出口压力。在最小压力位置的下游， 随着动能转换回静压能， 流动开始减速， 压力逐渐增加至局部最大值， 即出口压力。

(a) Single orifice model

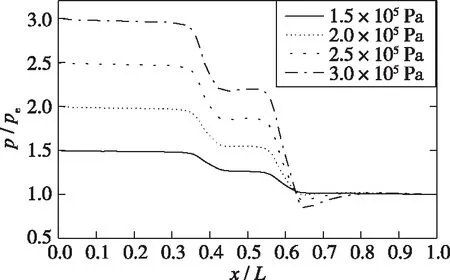
(b) Double orifice model图8 中心线压力分布Fig. 8 Centerline pressure distribution

图 9， 10分别为不同入口压力下通道中心线的速度分布和温度分布， 可以看出速度与温度的变化规律相反。孔口结构类似于一个收缩/扩张的装置， 因此气体在经过孔口时被压缩， 导致孔口处的速度增加， 其后， 由于通道扩张， 速度减小， 流场中温度变化与速度变化相反。在单孔结构中， 可以发现气流经过孔口时速度上升非常快， 由于惯性作用， 在离开孔口后速度达到最大， 再缓慢降低， 且流场的最大速度随着入口压力的增大而增大。在双孔模型中， 发现孔口1的速度变化幅度较小， 一方面孔口1的位置处于流场的前半部分， 本身速度就较低； 另一方面， 气体速度与压降大小有关。当入口压力为1.5×105Pa时， 由于两次压降大小几乎相同， 因此经过两个孔口速度增加量相似； 而当入口压力逐渐增加， 经孔口2的压降比孔口1要大得多， 因此， 孔口2的速度变化更剧烈。对比同一入口压力下两个模型的速度大小， 单孔口的最大速度要大于双孔口模型， 由于双孔口模型经两次压降， 在相同压差情况下， 双孔口的单次压降小， 使得流体速度每次增加的幅度也小。另外， 由于双孔口流场产生两处分离区， 流场扰动作用更加明显， 对流体的速度也产生了一定影响。

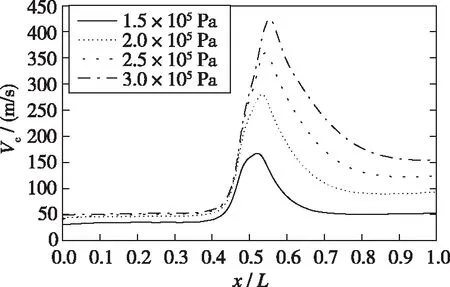
(a) Single orifice model

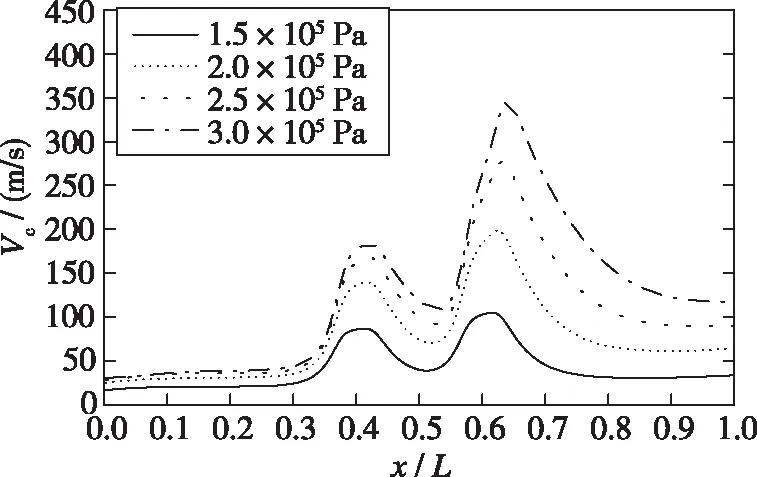
(b) Double orifice model图9 中心线速度分布Fig. 9 Centerline velocity distribution

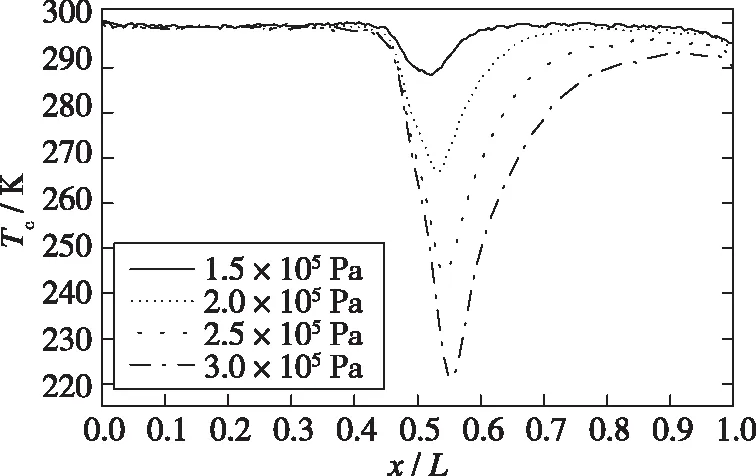
(a) Single orifice model

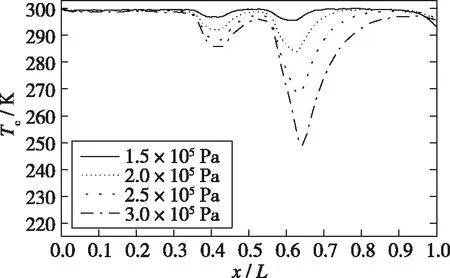
(b) Double orifice model图10 中心线温度分布Fig. 10 Centerline temperature distribution

5 结论

本文基于压力边界条件的DSMC方法， 研究了不同网格尺寸和时间步长对直微通道模型结果精度的影响， 得到了在微尺度下的网格尺寸和时间步长选取的一般准则。在此基础上， 研究了不同入口压力条件对单/双孔口结构微通道内流动过程的影响。主要得出以下结论:

(1) 通过CSL数和DCFL数两个无量纲参数给出了网格尺寸和时间步长的约束条件， 研究结果表面在满足DCFL数严格小于1的情况下， 选择CSL数接近或小于1， 可以作为网格尺寸与时间步长的选取原则。

(2)由于压降的存在使得孔口后形成低压区， 因此气体经过孔口后会在拐角处形成分离区， 并且分离区大小随入口压力的增大而增大。双孔口模型中， 两孔口之间的过渡区域流程较短， 但也出现了分离现象， 并随入口压力增大， 过渡区两处分离涡逐渐融合。在相同压差情况下， 通过双孔口模型流速会低于单个孔口通道的流速。

(3)在孔口模型中， 气流在通过孔口时产生较大压降。经孔口处的气流速度增加， 并随入口压力增大而增大。最大速度的位置由于惯性作用逐渐后移， 出现在孔口下游， 其后， 速度逐渐降低。温度与速度变化相反。