Arnoldi方法简述及其在流动稳定性中的应用
2022-10-14李武庸涂国华
李武庸, 涂国华, 陈 曦
(1. 云南大学数学与统计学院, 云南昆明 650500;2. 中国空气动力研究与发展中心空气动力学国家重点实验室, 四川绵阳 621000;3. 中国空气动力研究与发展中心计算空气动力研究所, 四川绵阳 621000)
引 言
矩阵的特征值问题可写为Ax=λx, 其中A∈Rn×n为矩阵,λ∈C为矩阵的特征值,x∈Cn为特征值λ所对应的特征向量; 特征值问题在科学和工程中应用非常广泛, 如流动稳定性问题, 楼房、 桥梁及涡轮机的防震设计, 电路网与动力系统中分支模式分析等[1]。一个最直接的特征值问题求解方法就是求解方程det(A-λI)=0。 除了一些特殊的矩阵(如三角矩阵)外, 该方法对于一般矩阵面临如下困难: 其一, 如果A的阶数比较大, 则方程det(A-λI)=0的计算量非常大; 其二, det(A-λI)=0的根不稳定。基于上述原因, 研究人员通常寻求其他求解方法。目前, 求解矩阵特征值问题的方法大体上可以分为两类: 变换法和迭代法。变换法是直接对原矩阵进行处理, 通过一系列变换, 使之变成容易求解特征值的形式, 如Jacobi方法、 Givens方法、 QR方法[2]等。
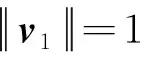

上述基于Arnoldi方法的改进都利用了投影矩阵的特征信息, Jia[29]证明了即使n阶矩阵A的Ritz值收敛,A的Ritz向量不一定收敛。为了克服这一弊端, 1997年, Jia[15,30-31]提出了改进的Arnoldi方法, 此方法通过最小化已收敛的Ritz值对应的剩余范数来优化Ritz向量。2006年曹陶桃[32]应用了求解大型非对称矩阵特征问题的精化Arnoldi-Chebyshev方法。然而采用基本的Arnoldi算法计算巨型矩阵的特征值和相应的特征向量, 会出现数值计算存储无限增长的情况, 限制了该方法的适用性。1992年, Sorensen[33]提出隐式重启Arnoldi方法, 此方法将Arnoldi过程中的迭代数固定为预先给定的值, 再利用已更新的初始向量重启Arnoldi过程。该迭代方案应用隐式位移QR迭代法, 避免了计算初始向量存储需求量大的问题。2015年Fazeli等[34]基于隐式重启Arnoldi方法提出了并行隐式重启Arnoldi方法, 此算法是隐式重启Arnoldi方法[35]的一个变体, 它以嵌套的方式生成多个子空间, 在每个重启周期内动态地选择最佳的子空间。2016年Fender等[37]基于隐式重启Arnoldi方法提出了并行混合Arnoldi算法, 并行性和计算机性能对计算收敛速度至关重要, 因此该方法使用了加速器并改进文献[38-39]中所提出的方法。
Arnoldi方法已在流向涡失稳、 后掠翼横流涡失稳、 接触线失稳、 三维边界层首次失稳问题等全局流动稳定性问题求解中得到广泛应用, 相关研究内容可参考综述[40-41]以及博士论文[42-44]。本文将利用Arnoldi方法的不同变体并结合谱位移技术去求解不可压Poiseuille流动稳定性问题、 超声速边界层稳定性问题和高超声速流向涡稳定性问题, 结果表明结合谱位移技术的多重隐式重启Arnoldi方法求解效率最高。
本文结构如下: 第1部分简述基本的Arnoldi算法; 第2部分简述基于Arnoldi算法的几类变体及谱位移技术; 第3部分通过求解具体的流动稳定性问题, 比较各方法的有效性。
1 基本的Arnoldi算法

展开最后一项得


span{v1,v2,…,vk}=span(v1,Av1,…,Ak-1v1)
上述过程称为k步Arnoldi分解[20,33], 可归纳为如下方程
AVk=VkHk+rkekT
其中,Vk=(v1,v2,…,vk),ek=Ik(:,k)
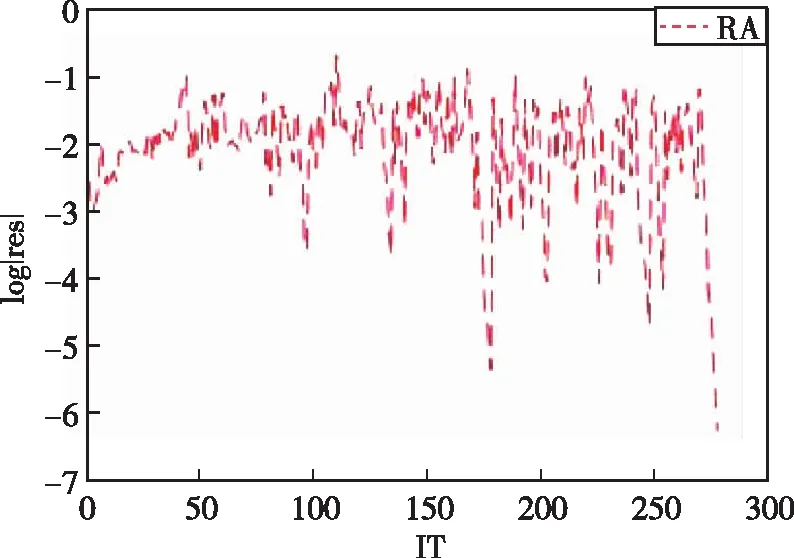
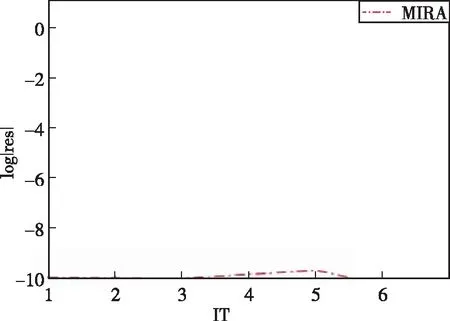
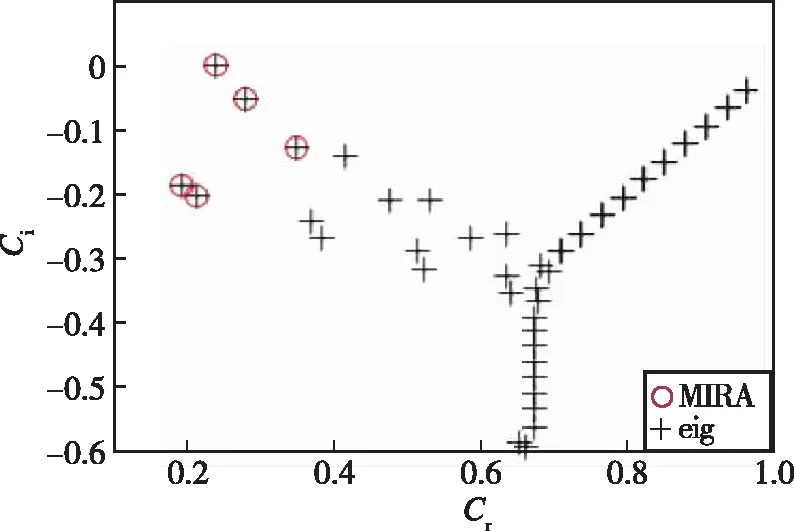
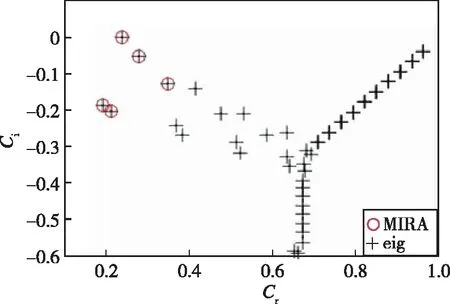
此Arnoldi分解过程可视为n×n阶矩阵A简化为k×k阶上Hessenberg矩阵H的过程, 适用于计算n阶巨型非对称矩阵A的近似特征对(λi,xi)i∈{1,2,…,n}, 将给定的巨型矩阵A逐步化简为上Hessenberg矩阵H。通过计算m(m< Arnoldi算法数值比较稳定, 但计算的每个基向量需要与前面计算出的所有基向量进行正交化操作, 随着计算的进行, 运算量和存储量都会增加。Arnoldi方法还需计算一个m阶Hessenberg矩阵的特征值和特征向量, 此方法的运算量为O(m3)。 因此, 为了节省存储和计算量, 重启通常是必需的。在实际应用中常采用重启Arnoldi算法及其变体, 即选取一个合适的m值, 用新的初始向量v+重新启动Arnoldi过程; 其中v+是所需特征向量对应Ritz向量的线性组合[22,24]。重启算法的思想是期望新的初始向量v+包含关于所需特征向量的更多信息。即, 将扩大在所需特征向量方向上的系数, 同时缩小在不需要的特征向量方向上的系数。为了提高重启Arnoldi算法的效率, 文献[24,27,33,36,46]研究了基于显式重启Arnoldi的一些加速技术。 考虑已运行m步的Arnoldi过程, 从Arnoldi向量v1,v2,…,vm中选择其线性组合为新的初始向量v+, 重新开始运行Arnoldi过程, 即:v1=v+。 由于Krylov空间的性质 span{v1,v2,…,vk}=span(v1,Av1,…,Ak-1v1) 因此v+的形式可为:v+=p(A)v1, 其中p(A)为次数不超过m-1的多项式。 假设A∈Cn×n可对角化, 且满足Axi=λixi,i=1∶n。若v1有特征向量展开的形式v1=a1x1+a2x2+…+anxn, 则v+为 x=a1p(λ1)x1+a2p(λ2)x2+…+anp(λn)xn 的系数倍。若p(λα)>>p(λβ), 则v+在xα方向上比在xβ方向上占比多。通过选择p(λ), 可得相应特征方向上的v+, 即它在某些特征向量方向上的分量被加强, 而在其他特征向量方向上的分量被弱化[47]。 例如, 若选取 p(λ)=c(λ-μ1)(λ-μ2)…(λ-μp) (1) 其中,c是常数,v+是沿a1p(λ1)x1+a2p(λ2)x2+…+anp(λn)xn方向上的向量。因此, 如果λβ接近滤波值μ1,μ2, …,μp中的某个, 而λα不接近; 则相对于xα而言,xβ方向不再被加强。因此, 从K(A,v1)中选取一个较好的重启向量v+就是选取一些多项式滤波来调出矩阵谱中不需要的部分[36,49]。 该算法流程如图1所示。 图1 显式重启Arnoldi算法流程图Fig. 1 Flow chart of explicitly restarted Arnoldi algorithm 隐式重启Arnoldi算法是1992年Sorensen基于 Arnoldi[33]重启过程提出的算法, 使用带位移的QR迭代法[50]隐式确定重启向量v+[33,35,51]。假设H∈Rm×m是上Hessenberg矩阵, 选取滤波值μ1,μ2, …,μp为位移QR法的位移, 则位移QR迭代算法如下 H0=H fori=1∶p qr(Hi-1-μiI)=ViRi Hi=RiVi+μiI end (2) 每个Hi,i∈(1,2,…,p)是上Hessenberg矩阵; 此外, 令 则H+=VTHV, 及 VR=(H-μ1I)…(H-μPI) (3) 则上述结果表明, 多项式滤波(1)等价于(2)。注意到, (3)中的矩阵R是上三角矩阵, 因此V(:,1)=p(H)e1。其中p(λ)是多项式滤波(1)且c=1/R(1,1)[2]。 若已用初始向量v1运行了c步Arnoldi迭代, 有 (4) AVce1=VcHe1 其中,V+=VcV。令v+为矩阵V+的第1列 v+=V+(:,1)=VcV(:,1) 式AVce1=VcHe1,表明对于任意的μ有 (A-μ·I)Vce1=Vc(H-μ·I)e1 因此 v+=c·(A-μ1I)…(A-μpI)Vce1 该算法流程如图2所示。 图2 隐式重启Arnoldi算法流程图Fig. 2 Flow chart of implicitly restarted Arnoldi algorithm 在隐式重启Arnoldi方法中子空间的大小凭经验选择, 若选择不当可能会导致结果误差偏大, 方法不收敛。多重隐式重启Arnoldi方法便是一种改进的隐式重启Arnoldi方法, 改进了隐式重启Arnoldi方法中凭经验选择子空间的大小这一弊端。此方法也称为多重隐式重启嵌套子空间Arnoldi方法, 它是基于巨型矩阵A投影在多个嵌套子空间上而不是单个子空间上[53], 再利用Arnoldi算法计算巨型矩阵A在一组嵌套的Krylov子空间上的Ritz元素, 其嵌套子空间为K(mi,v), (i=1,2,…,l),K(mi,v)⊂K(mi+1,v)。 若在这些子空间中计算的Ritz元素的精度不理想, 则选择这些子空间中Ritz元素精度“最佳”的所对应的子空间大小记为mbest。若残差R满足R(m1) 算法流程如图3所示。 图3 多重隐式重启Arnoldi算法流程图Fig. 3 Flow chart of multiple implicitly restarted Arnoldi algorithm 在谱空间中位于边缘处特征值对应的特征向量和其他特征向量有很大差异, 故边缘处的特征值容易求解。而聚集在一块的特征值对应的特征向量的方向很接近, 需要大量的迭代步数才能准确提取各个特征向量对应的特征方向。为有效地将所关注的特征值从谱中提取出来, 需要引入谱位移技术。谱位移技术就是在不改变原问题解的情况下, 将原始解对应的谱空间进行一定的变换, 把所需的特征值移到谱的边缘, 以便于求解。推导如下 谱位移技术的优势大致归纳为以下几点: (1)可以直接处理一些奇异矩阵问题。如求解广义特征值问题Ax=λBx时, 若B是个奇异矩阵。直接求解B-1A不可能, 若引入谱位移σ后, 则可以直接求解 (A-σB)-1B (2)可以计算谱内部的特征值, 不仅是那些特殊的特征值(模最大、 最小等), 还包括任意区间上的特征值。 (3)可以加速收敛, 在迭代法求解特征值问题的过程中, 特征值的收敛速度取决于特征值之间的距离, 通过谱位移技术可以直接将需要的特征值从聚集的特征值中提取出来, 从而加快迭代收敛速度。 下一部分我们利用上述所提3种方法结合谱位移技术求解流动稳定性问题, 经比较得出多重隐式重启Arnoldi算法更容易算出分布在谱边缘的特征值。Tezuka等[55]较详细地介绍了采用基本的Arnoldi方法求解特征值问题的过程, 并在三维不可压缩流动的稳定性分析中取得了成功。 利用上面介绍的Arnoldi方法及其变体求解流动稳定性的中3个典型问题, 即不可压Poiseuille流动稳定性问题、 超声速边界层稳定性问题和高超声速流向涡稳定性问题[56-57], 以展示各方法的优缺点。首先, 为不失一般性, 以不可压流动为例详细介绍流动稳定性方程的推导过程, 可压流动稳定性方程的推导过程见附录A。 只考虑不可压缩二维流动情形(Squire证明不可压缩流动的三维流动情形可归结为二维情况)[48] (5) 设主流方向沿x轴, 引入小扰动:u=U+u′,v=v′,p=P+p′代入式(5)得 (6) φ=φ(y)e[iα(x-ct)] (7) p′=π(y)e[iα(x-ct)] (8) 其中, 在时间模态下, 波数α是实数, 波速c=cr+ici是复数, 若ci<0, 则为稳定模态, 若ci>0, 则为不稳定模态, 若ci=0, 则为中性稳定模态。将式(8)代入小扰动方程(5)~(7), 得到 -αcφ′+iαUφ′-iαU′φ= (9) (10) (D2-α2)2φ=iαR[(U-c)(φ″-α2φ)-U″φ] (11) 即Aφ=cBφ, 其中 A=(D2-α2)2-iαR(UD2-Uα2-U″) B=iαR(α2-D2) 首先对Poiseuille流,U=1-y2, Orr-Sommer- feld方程(11)系数是关于x轴的偶函数, 而方程中微分的阶数是偶数, 故特征函数一定可以表示成奇模态(奇函数)和偶模态(偶函数)的线性组合, 其中每个奇、 偶模态都是该问题的特解。研究表明奇模态都是稳定的; 对偶模态, 边界条件为 φ‴(0)=φ′(0)=φ(1)=φ′(1)=0 在对称面处, 1阶和3阶导数等于零是偶函数自带的条件。将特征函数用N项Chebyshev 多项式来逼近 其中 T2n(y)=cos(2narccos(y)),y∈[-1,1] 是第n阶第1类 Chebyshev多项式。为确定N项未知系数, 考虑到有两个边界条件选定N-2个配置点 yj=cos(jπ/(2N-4)),j=1,2,…,N-2 设在N-2个配置点精确满足 Orr-Sommerfeld 方程, 考虑边界条件 整理后得矩阵特征值问题 Aφ=cBφ 计算条件为:Re=10 000.0; 流向波数α=1.0; Chebyshev配置点数N=100; 基本流分布U(y)=1-y2。 初始向量均为随机向量, 收敛误差均为10-10, 计算机设备条件为Intel(R) Core(TM) i5-5250U CPU @ 1.60GHz。数值结果见图4, 表1。 (a) RA (b) IRA (c) MIRA图4 给定谱位移参数σ=0.3情形下3种不同的Arnoldi方法求解的Poiseuille流扰动特征值问题的特征谱Fig. 4 Characteristic spectra of three different Arnoldi methods for solving the perturbation eigenvalue problem of poiseuille flow at the spectral displacement parameter σ=0.3 表1 3种方法求解不可压缩二维流动比较Table 1 Comparison of three methods for solving two-dimensional incompressible flow 在图4中, 子图(a)RA表示重启Arnoldi, 子图(b)IRA表示隐式重启Arnoldi, 子图(c)MIRA表示多重隐式重启Arnoldi。 黑色+为matlab中eig求解的特征谱。 在表1中“*”表示未满足误差要求。 结合图4与表1可知, 采用重启Arnoldi算法只有一个最不稳定的模态收敛, 其他模态并未收敛; 采用隐式重启Arnoldi算法5个模态都收敛, 但空间维数m凭经验选取为25耗时0.445 065 s, 耗时较长; 而采用多重隐式重启Arnoldi算法5个模态都收敛且只需一次迭代, 耗时最短。 由图5可知, 重启Arnoldi算法的最大残差的模一直在10-1~10-3附近徘徊, 直至280步左右下降至大约10-6处, 但达到迭代上限一直没有收敛; 隐式重启Arnoldi算法最大残差的模一开始就比较小, 迭代35步就降至10-10处; 而多重隐式重启Arnoldi算法的最大残差的模一开始就位于10-10处, 迭代3~5步同样在10-10周围浮动。 (a) RA (b) IRA (c) MIRA图5 3种不同的Arnoldi方法求解的Poiseuill流扰动特征值问题所对应的残差Fig. 5 Residual corresponding to the perturbation eigenvalue problem of poiseuille flow solved by three different Arnoldi methods 谱位移参数是特征值的初始猜测值, 由图6可见, 多重隐式重启Arnoldi方法在不同位移参数下, 皆能收敛到有效特征值; 特别地, 在从0.1~0.6的范围内, 多重隐式重启Arnoldi方法都能得到谱位移参数附近的模态, 说明该方法鲁棒性较好。 (a) σ=0.1 (b) σ=0.3 (c) σ=0.5 (d) σ=0.6 (e) σ=0.8 (f) σ=0.9图6 不同谱位移参数σ=0.1~0.9情形下多重隐式重启Arnoldi方法得到的特征谱Fig. 6 Characteristic spectra obtained by multiple implicitly restarted Arnoldi method under different spectral displacement parameters σ=0.1~0.9 下面考虑Ma=2.5超声速平板边界层的特征值问题[52]。采用与第1个算例相似的方法, 将流场分解为基本流和扰动场, 代入Navier-Stokes方程, 去掉基本流部分和扰动非线性项, 用Chebyshev配置点法离散后同样可得到特征值方程如下 A(y)q=wB(y)q,q=(u′,v′,p′,T′,w′) (a) RA (b) IRA (c) MIRA图7 3种方法分别求解Ma=2.5高超声速边界层稳定性与函数eig的比较Fig. 7 Comparison of three methods for solving hypersonic boundary layer stability at Ma=2.5 with function eig 表2 3种方法分别求解来流Ma=2.5的平板边界层流动比较Table 2 Comparison of three methods for solving the boundary layer on a flat plate at incoming Mach number Ma=2.5 最后考虑计算量更大的二维特征值问题, 以Ma=6高超声速6°攻角圆锥背风流向涡稳定性分析为例, 如图8所示, 等值线是背风流向涡的基本流; 云图是流向扰动速度特征函数实部分布。该流动情况下的边界层稳定性问题归结于求解如下二维特征值问题 图8 Ma=6高超声速6°攻角圆锥边界层背风流向涡不稳定模态特征函数分布Fig. 8 Characteristic function distribution of unstable modes of vortices in the leeward side of conical boundary layer at 6° angle of attack and hypersonic speed Ma=6 A2d(y,z)q=αB2d(y,z)q 其中,y,z分别为法向与展向坐标 q=(u′,v′,p′,T′,w′,αu′,αv′,αp′,αT′,αw′), 流向波数α为待求特征值; 法向边界条件为:u′=v′=T′=w′=0,展向为周期边界条件; 法向和展向分别用4阶中心差分离散, 得到巨型稀疏矩阵特征值问题, 分别用上述3种算法求解频率为 150 kHz 的不稳定模态, 结果如表3所示, 可见3种方法中多重隐式重启Arnoldi耗时最短且精度较高(达到收敛条件时剩余范数最小)。 表3 3种方法求解不可压缩二维流动比较Table 3 Comparison of three methods for solving two-dimensional incompressible flow 本文对重启Arnoldi方法、 隐式重启Arnoldi方法、 多重隐式重启Arnoldi方法作了介绍; 指出重启Arnoldi算法凭经验选择子空间的大小, 若子空间大小选择不合适会导致结果误差偏大, 所求的模态不收敛, 并且该算法还需显式计算重启向量, 随着计算的进行此算法的运算量和存储量都会增加。隐式重启Arnoldi算法有效地改进了重启Arnoldi算法中显式计算重启向量时所需时间与空间这一弊端, 但子空间的大小仍凭经验选择。多重隐式重启Arnoldi算法改进了前两种方法中凭经验选择子空间大小, 此方法迭代次数较少, 耗时较短。最后将上述方法应用于3个典型的流动稳定性问题求解中, 结果表明结合谱位移技术的多重隐式重启Arnoldi方法求解效率最高。2 Arnoldi算法的变体
2.1 显式重启Arnoldit算法
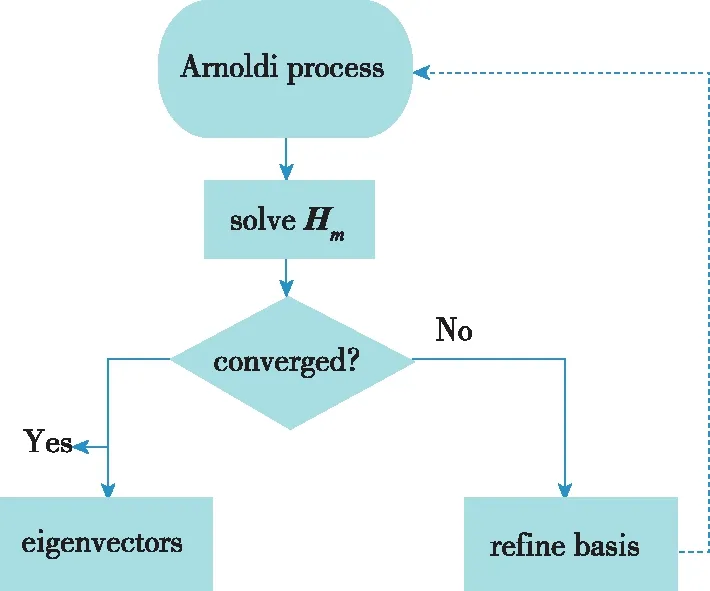
2.2 隐式重启Arnoldi算法
H+=Hp
=c·Vc(H-μ1I)…(H-μpI)e1
=p(A)v1=Vc·V(:,1)
2.3 多重隐式重启Arnoldi算法

2.4 谱位移技术


3 数值实验
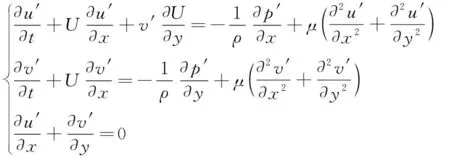
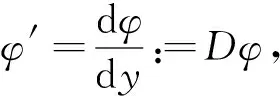
3.1 Poiseuille流扰动特征值问题
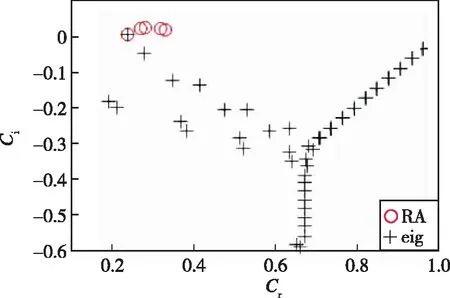
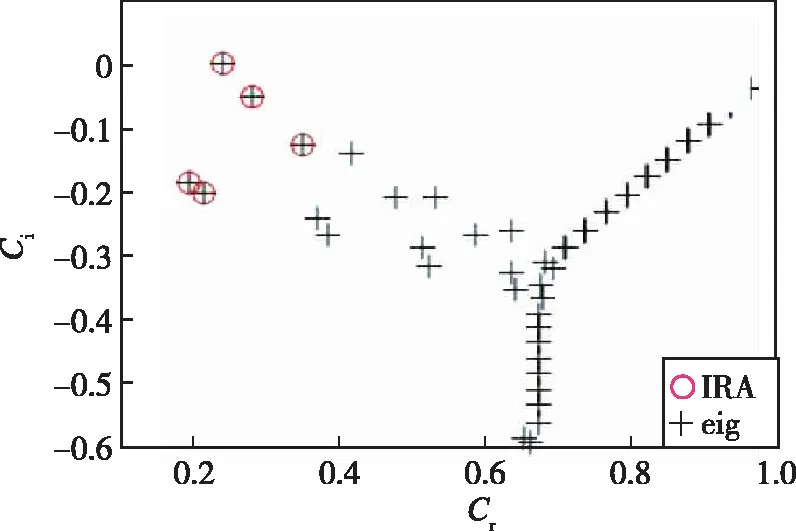
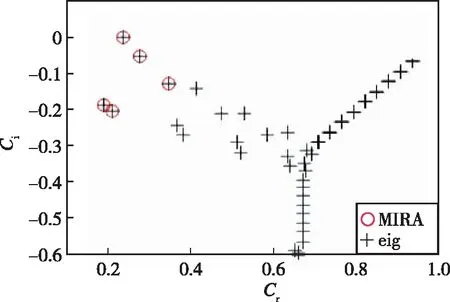
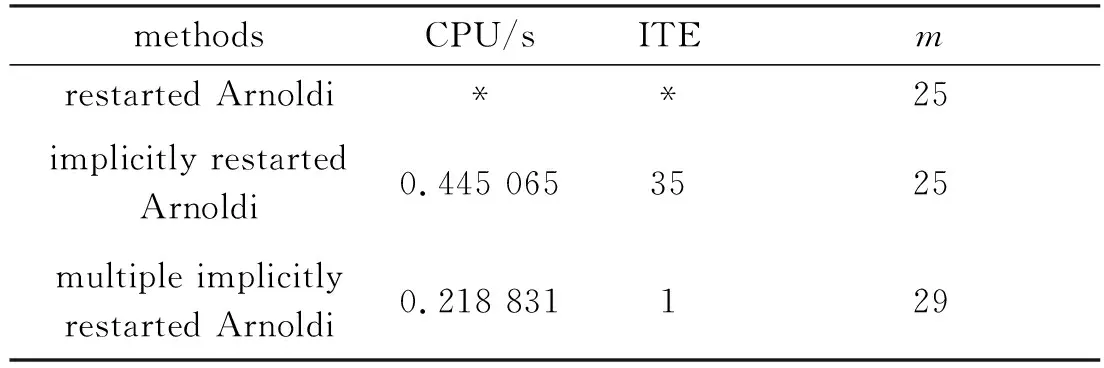


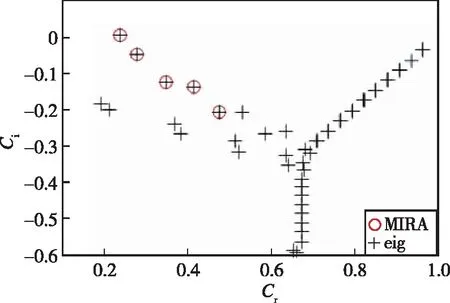

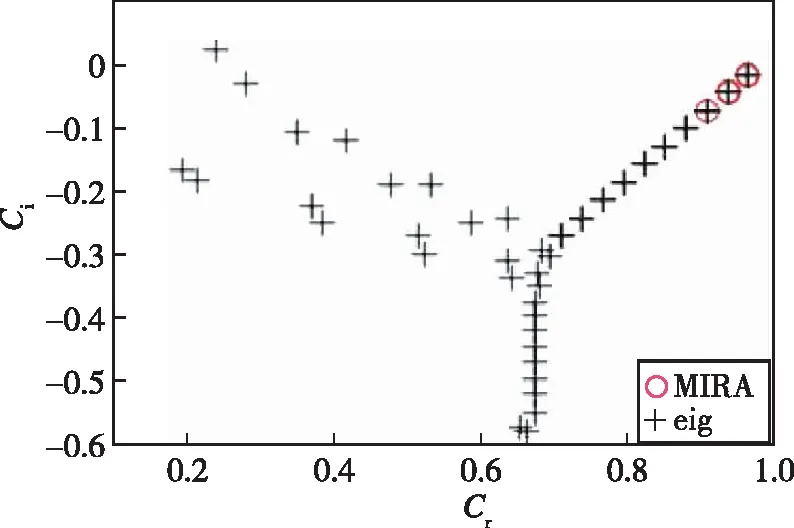
3.2 Ma=2.5超声速平板边界层的特征值问题

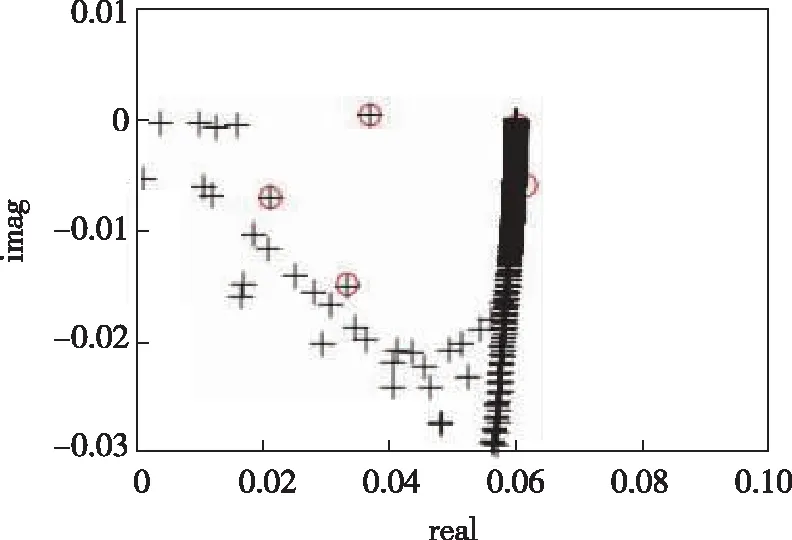
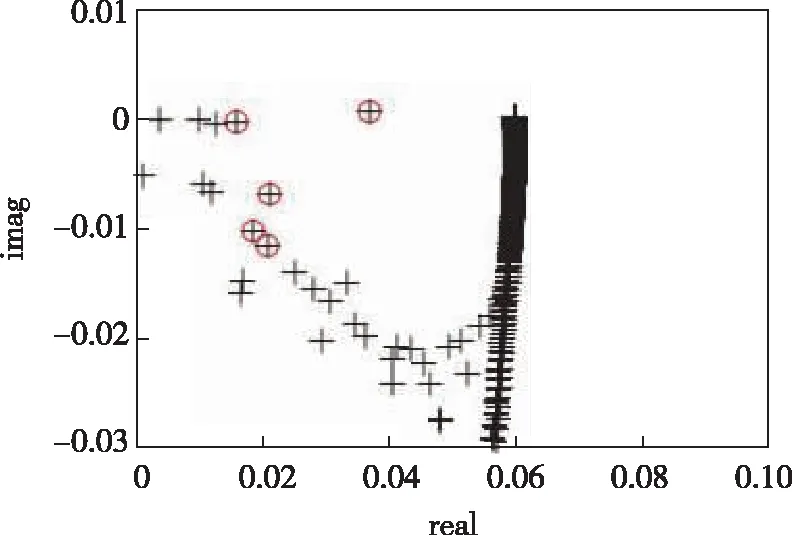
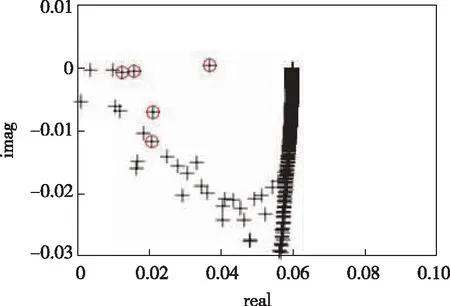
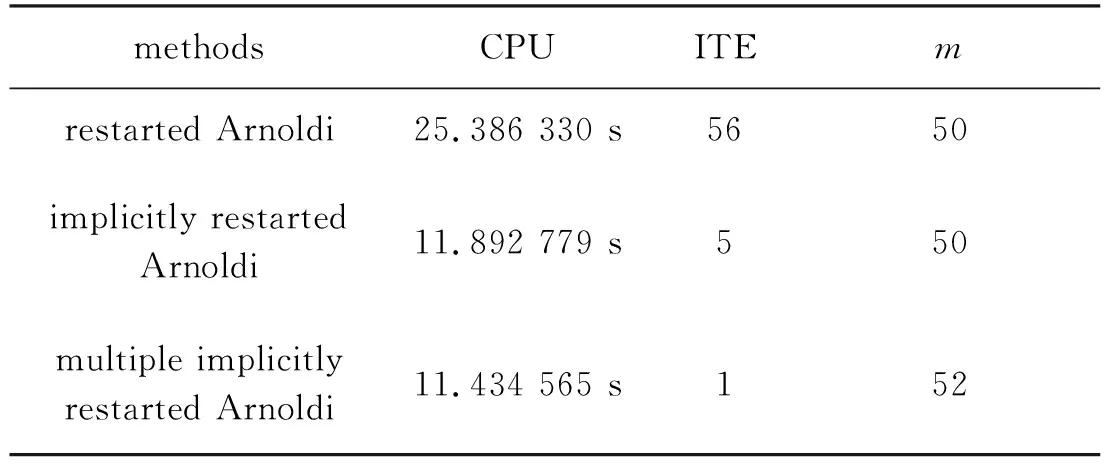
3.3 Ma=6高超声速6°攻角圆锥背风流向涡稳定性分析

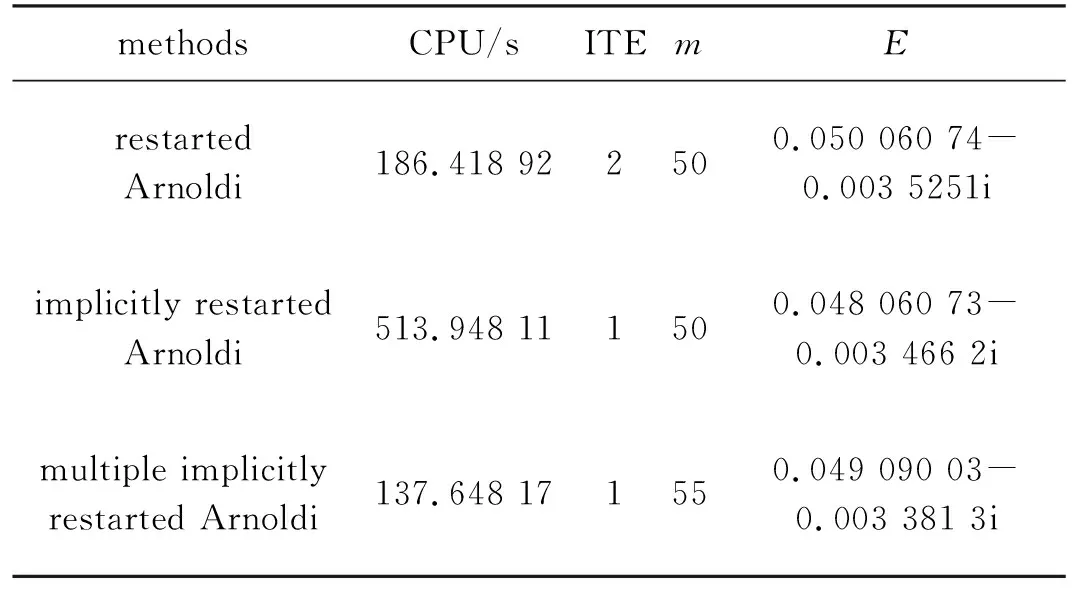
4 结论
