中美两本微积分教材中导数的定义

阮玉洁 王 敌 王红丽

(1.大连大学经济管理学院，辽宁 大连 116622；2.大连大学机械工程学院，辽宁 大连 116622;3.大连大学信息工程学院，辽宁 大连 116622)

一、引 言

同济大学高等数学教研室编写的《高等数学》(第七版)(以下简称同济版)是我国高校理工类专业普遍使用的一本经典教材导数是高等数学中重要的概念之一，同济版教材对导数的定义进行了全面的阐释，但是关于什么是“导数不存在”并没有给出一个明确的定义，因此学生在学习过程中会产生这样的疑问：如果导数即等同于导数存在，那么“导数不存在，可否写作′()不存在”，如果不可以写，那么在习题中出现的′()不存在又如何理解呢？或者说() 在=处不可导是否等同于′()不存在？本文用美国高校普遍使用的，由Dale Varberg 等编写的《微积分》(第九版)(以下简称Varberg版)教材的导数定义来解决上述问题

二、两本教材关于导数的不同定义

1同济版教材导数的定义

设函数=()在()内有定义，当在处取得增量Δ(点+Δ仍在该领域内)时，相应地，取得增量Δ=(+Δ)-()；如果Δ与Δ之比当Δ→0时的极限存在，那么称函数=()在点处可导，并称这个极限为函数=()在点处的导数，记为′()，即

函数()在点处可导有时也说成()在点具有导数或导数存在

1求函数()=||在=0处的导数

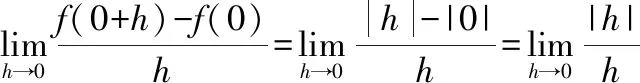
当<0时，

故

当>0时,

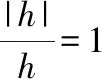
故

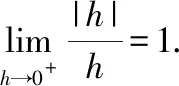
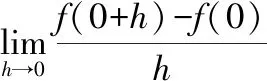
这个例子是大多数微积分教材上都会给到的例子，大家可以看到在解题的最后是通过函数在=0处不可导来描述的那么我们在做这样的题目时，会用“函数在=0处的导数不存在”来描述还是写作“′(0)不存在”呢?

浙江大学的苏德矿老师也讲过这道例题，他在讲完函数()=||在=0处不可导之后，又特别强调了这道例题的结论如果写成“′(0)不存在”这种写法是矛盾的，因为′(0)是当()=||在=0处可导时才给出来的记号，现在()=||在=0处不可导，所以写为“′(0)不存在”是矛盾的(见中国大学苏德矿微积分第二十四节：左右导数定义，导数与连续的关系)

2Varberg版教材导数的定义

The derivative of a function f is another function f ′(read “f prime”)whose value at any number x is

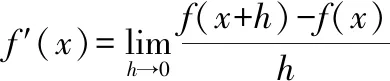
If this limit does exist，we say that f is differentiable at x.Finding a derivative is called differentiable;the part of calculus associated with the derivative is called differential calculus.

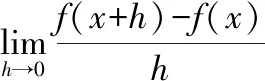
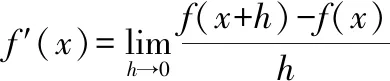
同样，在文献[2]第103页也给出例题1的解答：

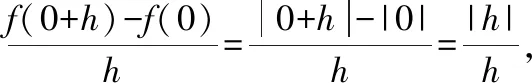
Thus,

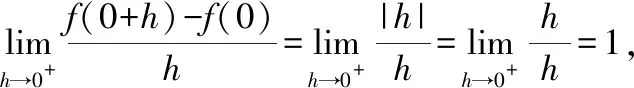
Where as，

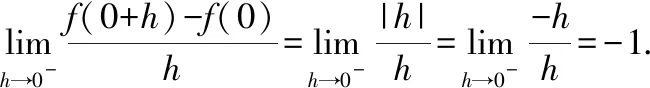
Since the right-hand and left-hand limits are different，

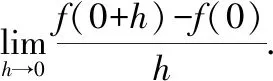
Does not exist.Therefore,′(0)does not exist.

我们可以看出，这本微积分的教材最后的结论是“′(0)does not exist.”

由此，我们可以看出，在Varberg版微积分中，有导数存在，导数不存在的定义，也可以写作′()不存在

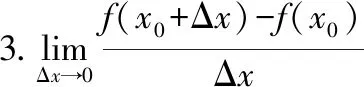
文献[1]教材其中几个有关于“导数不存在”以及“′()是否存在”的习题

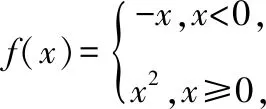
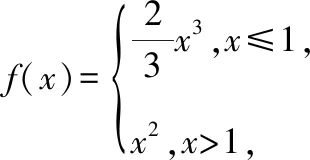
则()在=1处的( )(见文献[1]内第83页7题)

(A)左导数、右导数均存在

(B)左导数存在，右导数不存在

(C)左导数不存在，右导数存在

(D)左导数、右导数均不存在

三、从广义积分概念的改进来思考导数定义的改进

1广义积分定义的改进

以上内容是对无穷限广义积分定义的改进，我们注意到文献[1]中的第256页的广义积分定义正是采用的改进后的无穷限广义积分的定义31

2导数定义的改进

根据广义积分定义31的改进，结合美国微积分教材表述,我们将对导数定义加以改进,给出如下导数定义

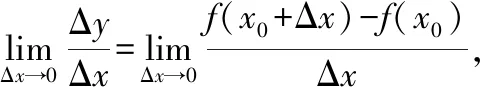
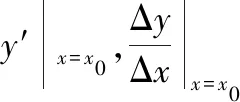
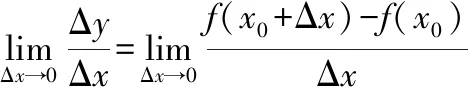
下面以这种定义方式求解例2

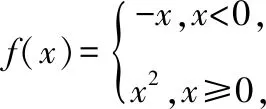
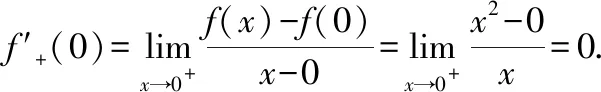
四、结 语

感谢微积分专题领学团队指导教师的指导！