基于五轴数控的整体硬质合金钻头螺旋槽磨削方法研究
2022-10-12张照耀郑君民陈毅赵剑峰佟谣
张照耀,郑君民,陈毅,赵剑峰,佟谣
大连交通大学机械工程学院
1 引言
整体硬质合金钻头广泛应用于现代机械制造业中。螺旋槽的磨削加工是钻头生产制造中的重要工序,砂轮在磨削过程中的轮廓形状和位姿决定了螺旋槽的轮廓。对于螺旋槽的研究工作主要集中于螺旋槽的建模和加工,一般可分为直接法和间接法。直接法是根据磨削过程中给定的砂轮轮廓及其位姿计算螺旋槽的截面轮廓;间接方法是根据砂轮位姿和所需要的螺旋槽轮廓确定砂轮轮廓[1]。然而,间接方法计算出来的砂轮形状往往很复杂,在工业上并不实用。因此,研究标准砂轮在五轴数控工具磨床的磨削加工方法具有重要意义。
复杂几何形状刀具的磨削与数控磨床加工中的一些复杂运动过程有关,国内外研究者对于螺旋槽磨削和刀具制造进行了广泛的研究。肖思来等[2]基于无瞬心包络法建立了变参数螺旋槽的数学模型,提出使用B样条曲线插值曲面描述螺旋槽的思路和方法。Guo C.L.等[3]提出了基于啮合理论的纯解析方法,利用给定的砂轮轮廓和砂轮与工件的相对运动,精确计算螺旋槽的数学模型。Ren L.等[4]提出利用标准1V1/1A1砂轮,基于解析几何和包络理论建立非线性方程组求解砂轮位姿,保证螺旋槽的芯厚、前角和槽宽。Li G.C.等[5]基于微分几何和单参数曲面包络理论,建立了砂轮的运动轨迹和由砂轮锥面生成的包络面方程,得到螺旋槽的数学模型。螺旋槽的形状对于任何钻头的设计都至关重要,Hsieh J.F.[6]建立了在六轴工具磨床加工时的螺旋槽轮廓或刀具轮廓通用数学模型,并对其灵敏度进行了分析。Tang F.等[7]详细研究了硬质合金钻头螺旋槽数学模型,通过控制螺旋槽的关键参数螺旋角、钻芯直径和前角,利用计算机编程方便快捷地计算砂轮位姿,克服经验公式精度低的问题,提高了硬质合金钻头螺旋槽设计的灵活性。
本文通过分析钻头螺旋槽磨削成型原理,基于啮合原理[8]和解析几何,提出了采用标准砂轮在五轴数控工具磨床上进行螺旋槽磨削的精确方法。采用这种方法可以根据螺旋槽的设计参数,精确求解出砂轮与工件做螺旋运动的相对位姿。根据砂轮位姿参数并通过后置处理得到五轴数控磨削加工的NC程序。利用VERICUT软件进行加工仿真并进行仿真数据测量,验证了该方法的可行性和准确性。
2 螺旋槽建模
2.1 砂轮数学模型
目前,在五轴数控工具磨床上采用标准砂轮磨削刀具螺旋槽的方法得到了广泛应用。图1为标准1V1/1A1砂轮,决定砂轮轮廓形状的参数包括砂轮半径RS,砂轮宽度H和砂轮轮廓倾斜角η。其中,1A1砂轮被认为是倾斜角η=0的标准1V1砂轮。

图1 标准砂轮模型
以1V1砂轮为例,建立砂轮坐标系OS-XSYSZS,YS轴沿砂轮轴线方向,XSOSZS平面位于砂轮大端面圆内,则砂轮的参数表达式为
(1)
式中,h为砂轮厚度参变量,h∈[0,H];α为参数角,α∈(0,2π]。
2.2 螺旋槽数学模型
在螺旋槽磨削过程中,砂轮相对于棒料做螺旋运动,磨削形成螺旋槽。本文基于直接方法建模,即已知砂轮轮廓形状和加工相对位姿,求解螺旋槽槽型。将砂轮离散成无限个一定厚度的薄圆盘,螺旋槽曲面由这些圆盘产生不同的切削路径包络而形成。建立如图2所示的坐标系,其中,工件坐标系O-XYZ固定在棒料上,圆心O位于棒料端面圆心上,X轴与棒料轴线重合;砂轮坐标系OS-XSYSZS固联在砂轮上,圆心与砂轮大端面圆中心重合,YS轴与砂轮轴线方向一致。已知砂轮轮廓模型,则螺旋槽槽型轮廓由砂轮初始安装角度γ和圆心初始位置(px,py,pz)决定。

图2 磨削过程砂轮位置
将砂轮坐标系中的坐标转换到工件坐标系的矩阵变换公式为

(2)
则工件坐标系中砂轮的参数方程可表示为
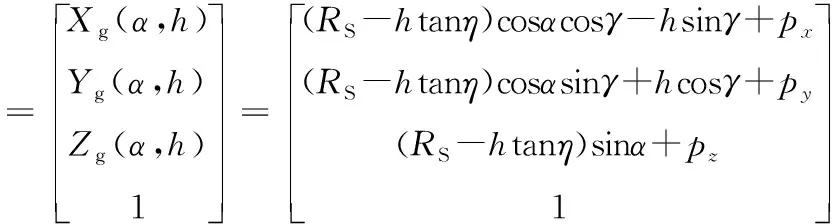
(3)
确定砂轮初始位姿后,砂轮以一定姿态绕棒料轴线做螺旋运动,导致材料去除形成螺旋槽,则螺旋运动的数学表达式为

(4)

联立式(3)和式(4),得到工件坐标系中螺旋槽曲面参数方程有
(5)

(6)
3 砂轮位姿求解
3.1 建立参数方程
钻头的前角、芯厚和螺旋角是螺旋槽的关键参数,对钻头的钻削性能、刚度、排屑以及容屑能力有较大影响。因此,在整体硬质合金钻头螺旋槽加工时要保证螺旋角、前角和芯厚,才能获得理想的螺旋槽。
为了避免螺旋槽在磨削过程中发生干涉,引入了切削角的概念,同时芯厚形成角则是为了得到满足要求的芯厚。该工步的关键在于根据槽型参数建立参数方程,并对芯厚形成角进行优化求解,进一步得到砂轮在工件坐标系下的初始安装角度和圆心坐标(见图3)。

图3 砂轮初始位姿
在图3所示坐标系中,设棒料半径为R,砂轮半径为R1。初始时刻,砂轮与XOZ平面平行,砂轮与棒料的切点坐标OR=(0,0,R),砂轮大端面圆的圆心坐标记为OS=(0,0,R+R1)。砂轮过切点OR依次绕Z轴方向向量旋转螺旋角θ,绕方向向量kθ旋转法前角φ,然后绕方向向量kθ旋转切削角σ,最后绕方向向量kφ旋转芯厚形成角φ。采用优化算法对其进行迭代求解,计算芯厚形成角φ。
砂轮的参数方程可表示为
r(R1,ε)=[R1cosε,0,R+R1+R1sinε]T
(7)
φ=arctan(tanδcosθ)
(8)
kθ=Rot(z,-θ)i0
(9)
kφ=Rot(kθ,φ)Rot(z,-θ)j0
(10)

对于绕空间任意单位向量N=(u,v,w)T旋转ξ角的矩阵变换公式有

(11)
工件坐标系中砂轮参数方程的矩阵变换为
(12)
对式(12)进行化简得
r4(R1,ε)=Rot(kφ,φ)Rot(kθ,σ)Rot(kθ,φ)
Rot(z,-θ)[r(R1,ε)-OOR]+OOR
(13)
砂轮最后绕方向向量kγ旋转芯厚形成角φ后,此时砂轮上有且仅有一点到钻头轴线的距离为r,即砂轮与钻头棒料芯厚相切,则满足下列等式
(14)
式中,s为切削长度;μ为参数角,μ∈[0,2π];r为钻头芯厚半径。
联立式(7)~式(11)、式(13)和式(14)可得
F(ε,φ,r)=0
(15)
式(15)包含ε和φ两个未知数,利用数学计算软件对其进行迭代求解,可求得当砂轮与钻头芯厚相切时,砂轮参数角ε有唯一值,对应芯厚角φ。可以进一步求解砂轮在工件坐标系下的初始砂轮空间位置和砂轮法向量。
3.2 参数方程求解
由式(15)求解得芯厚形成角,则可知在工件坐标系下砂轮经过一系列变换后的法向量j1和磨削端面圆的圆心坐标OO4。
砂轮法向量的表达式为
j1=Rot(kφ,φ)Rot(kθ,σ)Rot(kθ,φ)Rot(z,-θ)j0
(16)
砂轮磨削端面圆的圆心坐标为
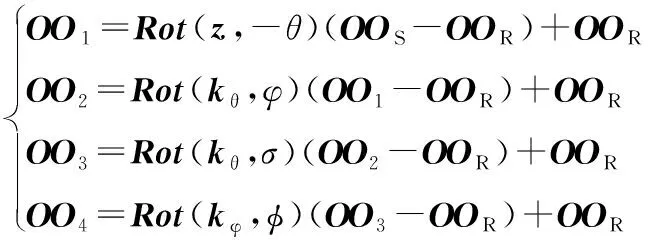
(17)
对式(17)化简可得
OO4=Rot(kφ,φ)Rot(kθ,σ)Rot(kθ,φ)
Rot(z,-θ)(OOS-OOR)+OOR
(18)
螺旋槽的设计参数见表1,根据上述方程利用数学计算软件对其进行优化求解,得到磨削参数见表2。

表1 螺旋槽初始参数

表2 求解的磨削参数
为了求解砂轮初始安装角度,将砂轮法向量j1绕X轴旋转至与Z轴相互垂直的位置,此时的旋转角度即为相对旋转角θA,矩阵变换公式为
(19)
式中,θA为绕X轴旋转角度。
此时砂轮法向量记为j2,有
j2=Rot(x,θA)j1
(20)
由砂轮法向量j2与Z轴相互垂直可得
j2k0=0
(21)

联立式(20)和式(21),求解得到旋转角θA。
此时砂轮磨削端面与X轴之间的夹角记为γ,砂轮法向量j2,X轴方向向量i0,则有
(22)
在实际计算γ过程中,需要对γ角进行调整,令t=i0j2,若t=i0j2>0,则γ=γC;若t=i0j2<0,则γ=-γC。
砂轮绕X轴旋转θA角后,则此时砂轮圆心坐标记为O5,有
OO5=Rot(x,θA)OO4
(23)
至此,根据已知参数求解得到砂轮的初始安装角度和磨削端面圆心坐标,通过该算法可以快速计算出不同参数下砂轮安装角度和砂轮圆心相对于工件坐标系原点的偏移量,此算法具有较强的通用性和拓展性,为以后研究刀具磨削软件系统奠定了基础。
4 五轴工具磨床的后置处理
后置处理的关键是机床运动求解,即根据机床的结构和各轴之间的运动关系,把工件坐标系中包含刀具方向矢量和刀具中心位置矢量的刀位数据转化为机床坐标系中数控机床各坐标轴的运动坐标[9]。根据图4所示的五轴数控磨床结构,对上述砂轮位姿参数通过后置处理算法求解得到NC代码。

图4 虚拟五轴数控工具磨床
图中,五轴工具磨床包含3个平动轴(X,Y,Z)和2个转动轴(A,C),其中C轴的回转轴为Z轴,A轴的回转轴为X轴。由于工件装夹在五轴工具磨床上,工件坐标系与机床坐标系不一致。
为了降低计算难度,需将工件坐标系旋转至与机床坐标系的方向一致。则旋转矩阵M1可表示为
M1=Rot(z,π)
(24)
为了更准确地描述五轴工具磨床各坐标系之间的转换关系,建立如图5所示的后置处理求解坐标系。
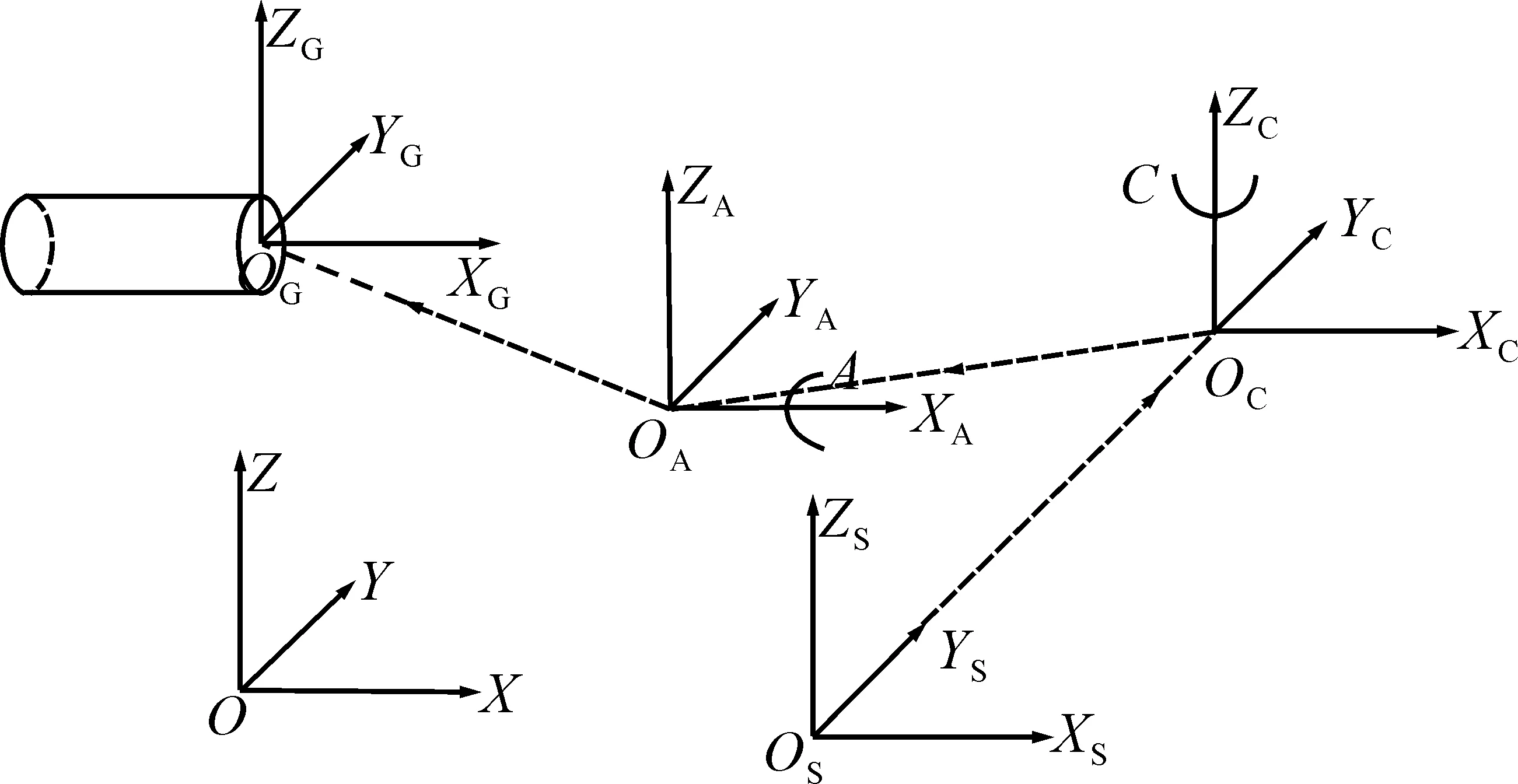
图5 后置处理坐标系运动链
后置处理坐标系运动链包括机床坐标系O-XYZ,旋转坐标系OA-XAYAZA和OC-XCYCZC,工件坐标系OG-XGYGZG,砂轮坐标系OS-XSYSZS。将砂轮的轴向方向向量和刀位点坐标从砂轮坐标系中转换到工件坐标系中,其转换关系可表示为
RG=Rot(x,-A)Rot(z,C)RS
(25)
PG=Rot(x,-A)Trans(x+LG,y,z)
Rot(z,C)Trans(0,LS,0)PS
(26)
式中,RG,PG为工件坐标系中砂轮法向量和磨削端面圆心坐标;RS,PS为砂轮坐标系中砂轮法向量和磨削端面圆心坐标;LG和LS分别为工件伸出长度和砂轮法兰长;-A为A轴旋转角度;-C为C轴旋转角度;x,y,z分别对应各平移运动轴的位移坐标。
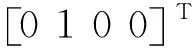
(27)
(28)
对式(27)求解得到角度A和C,有
(29)
由式(28)求解得到各平移轴的移动坐标为
(30)
将上述求解得到的砂轮位姿坐标和砂轮法向量代入式(29)和式(30)中,得到驱动五轴磨床各运动轴运动的NC程序。假设LS=240mm,LG=60mm,所得的部分加工G代码见表3。

表3 部分加工G代码
5 仿真验证
利用VERICUT仿真软件创建五轴工具磨床仿真系统,将工件轴线、砂轮轴线与主轴Z轴三线交点记为虚拟机床零点。加载上文求解的驱动机床运动的G代码,进行加工仿真验证,仿真结果如图6所示。通过VERICUT仿真软件测量工具对关键参数进行测量,结果见表4。可知,测量值与设计值结果满足设计精度的要求,证明了该算法的可行性和准确性。

图6 VERICUT仿真结果
为了进一步验证该算法的可靠性,通过改变螺旋槽槽型参数,对螺旋槽轮廓形状进行仿真模拟,研究不同参数对螺旋槽横截面的影响。表1中其他参数不变,前角依次设定为6°,10°,14°,观察螺旋槽横截面仿真结果如图7所示。将切削角依次设定为4°,8°,12°,同时表1中其他参数不变,得到仿真结果如图8所示。
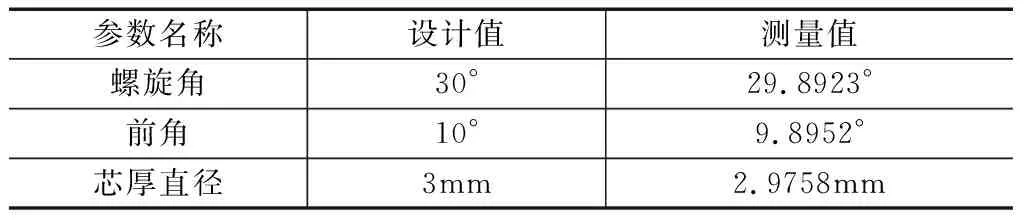
表4 测量值与设计值对比

图7 不同刀具前角时的螺旋槽轮廓仿真结果

图8 不同切削角时的螺旋槽轮廓仿真结果
对比图7和图8可以看出,通过改变设计参数得到不同的螺旋槽槽型。分析可知,随着刀具前角或切削角的增大,螺旋槽槽型轮廓及槽宽均有明显的差异。通过设定不同的前角或切削角得到不同的螺旋槽轮廓,极大地提高了整体硬质合金钻头螺旋槽磨削的灵活性。
6 结语
本文通过分析钻头螺旋槽磨削工艺特点,提出了一种采用标准砂轮进行五轴数控磨削螺旋槽的方法。该方法可以根据螺旋槽的设计参数,精确求解出砂轮与工件做螺旋运动的相对位姿,保证螺旋槽前角、芯厚和螺旋角等关键参数的精度。VERICUT软件仿真结果表明,采用这种方法加工的槽型参数与设计值基本一致,验证了该方法的可行性和准确性。
