一种解决函数同构问题的待定系数法

浙江省宁波市镇海中学 (315200) 杨冬冬

此题的难点在于解出方程x2ex+lnx=0的超越解，同构法技巧性强，学生不易掌握，鉴于此笔者发现一种待定系数法可解决此类问题，与大家分享.

例1 化简e2x-2x2=2xln2x.

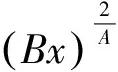
例2 已知e2x-4=xlnx+2x，求x-lnx的值.

其实此待定系数法不仅可解以上例题中的超越方程，对于有些不等式问题亦可处理.

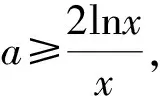
例4 (2020年高考山东卷)已知函数f(x)=aex-1-lnx+lna．

(1)当a=e时，求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积；(2)若f(x)≥1，求a的取值范围．

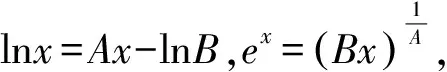
此方法适合解决一类含有指对式的超越函数或者超越方程问题，但并不是所有的问题都适用，比如超越函数中那些能求出极值点的问题，或者超越方程具有解析解的问题，不必要用此法.特别的，一类超越函数存在极值点，但极值点不可求，反而要求此时的极值，那么它往往可用此待定系数法解决.总而言之，要求学生有足够的解题经验与解题方法，在“变化”中寻求“不变”量，会“一法”而通“万题”.