由一道菱形证明题引发的思考

湖南省长沙市长郡月亮岛学校 (410200) 张月梅

菱形是一类特殊的平行四边形，具有平行四边形的共性和自身一些特殊性质，是初中几何教学的重点和难点，也是中考命题热点，经常与其他基本图形结合进行考察. 本文通过一道菱形背景的几何证明题，在梳理解题方法的同时，重在探究图形内部的联系.

图1

1.原题重现

如图1，已知菱形ABCD中，∠BAD=120°，M为BC上一点，N为CD上一点.求证：若△AMN有一个内角等于60°，则△AMN为等边三角形.

2.思路分析

要证明△AMN为等边三角形，已有一内角为60°，只需证明△AMN中有两边相等即可.由于60°角位置不确定，需分∠MAN=60°、∠AMN=60°和∠ANM=60°三种情况讨论，其中后两种情况证明方法相同.

3.解法展示

如图2，连接AC，易证△ABC和△ACD为等边三角形，可得AC=AD，∠ACB=∠DAC=∠D=60°.

图2

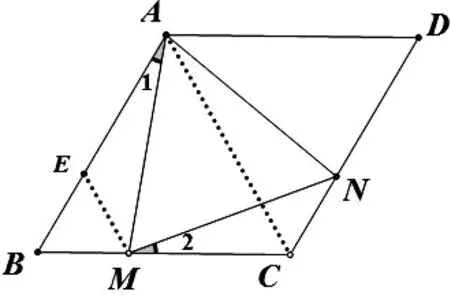
图3

(1)若∠MAN=60°，则∠1+∠2=∠2+∠3=60°，所以∠1=∠3，可证△AMC≌△AND，得到AM=AN，进而完成证明.

(2)若∠AMN，如图3，∠B+∠1=∠AMN+∠2，所以∠1=∠2.过点M作ME∥AC交AB于点E.易得△BEM为等边三角形，所以BE=BM，∠BEM=60°，得到AE=MC，∠AEM=∠MCN，可证△AEM≌△MCN，得到AM=MN，进而完成证明.

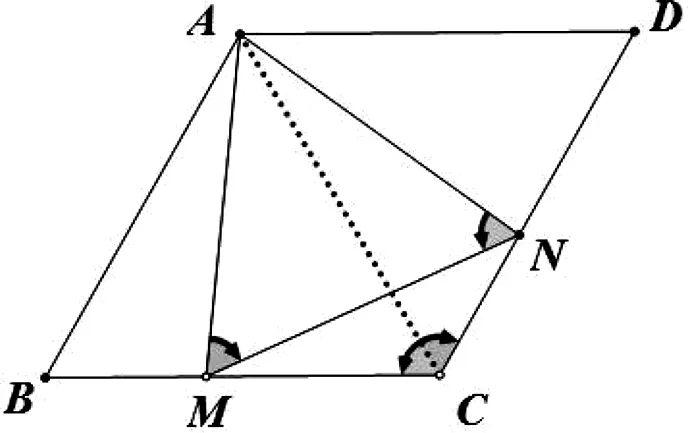
图4

若∠AMN=60°，还可以运用四点共圆方法创造条件进行证明.

如图4，由∠ACD=∠AMN=60°，所以A、M、C、N四点共圆.所以∠ANM=∠ACB=60°，进而得到△AMN三个内角均为60°，所以△AMN是等边三角形.

(3)若∠ANM=60°，证明方法与(2)中相同，此略.

上面的解法中，(1)运用的是“角边角”证明三角形全等的方法，(2)中方法一是“截长”构造等边三角形，得到三角形全等的条件，方法二则是利用四点共圆判定方法，先得到A、M、C、N四点共圆，再利用“同圆中相同的弧所对的圆周角相等”，得到∠ANM=∠ACB=60°，从而完成证明. 本题是多种几何证明方法的综合运用，很好地展现了菱形和等边三角形这两类初中几何常见几何图形组合在一起，并蕴含丰富的数学思想.

4.解后探究

图5

(1)原题给出含有一个60°内角的菱形，同时要求“内置”三角形有一个内角为60°，最终得到了“内置”三角形为等边三角形的结论. 若将条件改为：如图5，在菱形ABCD中，AC=AB，BM+DN=AB，可通过证明△ABM≌△ACN，证得“内置”△AMN为等边三角形.

(2)菱形ABCB′可看成由等腰三角形△ABC沿底边AC翻折180°与原来三角形一起所成的图形，也可看成由一个直角三角形Rt△ABO通过翻折(旋转)得到，如图6所示. 所以菱形的性质可由三角形中相关性质推导得出.

图6