一道解几压轴题的推广与拓展

福建省福清第一中学 (350300) 叶诚理 林品玲

探索性的问题历来倍受高考亲睐，它有利于考查学生的思维品质和学习潜能；有利于培养学生发现问题、分析问题、解决问题的能力和创新意识．一个探索性问题，往往蕴含丰富的数学知识、性质，常是学习者探求一类问题的“窗户”.本文以一道某地质检解几压轴题为例，它的背后隐藏着圆锥曲线的一个美妙性质，以下是笔者对此问题的推广与拓展.

1 试题引思，探寻问题本质

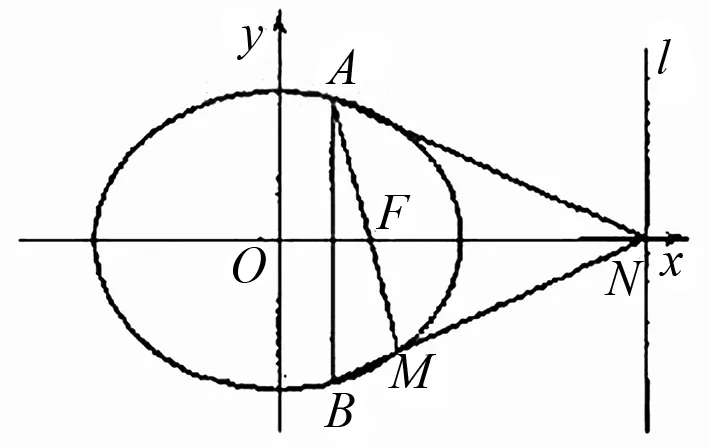
图1

(Ⅰ)求椭圆C的方程；(Ⅱ)若AB为垂直于x轴的动弦，直线l:x=4与x轴交于点N，直线AF与BN交于点M．求证：点M恒在椭圆C上.

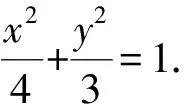
经验证，直线l恰为椭圆C的右准线，且点M恒在椭圆C上的性质不受椭圆方程中a,b取值的影响．

2 纵向推广，归纳一般结论

上述试题研究的是一特殊椭圆的性质，根据特殊到一般的思想，可得：

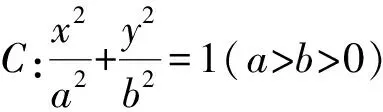
3 逆向思考，猜想新的性质

根据探求猜想1的思路，可逆向思考，交换条件与结论，得：

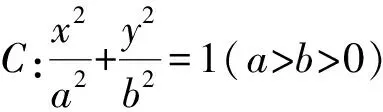
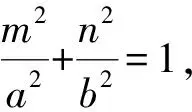
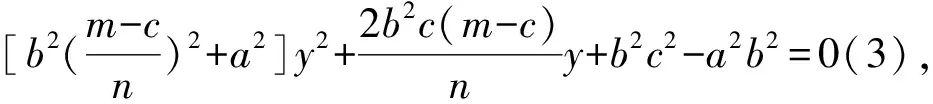
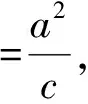
其他圆锥曲线是否也具有类似猜想1、2的性质呢？

4 横向联系，类比相似性质

类比在解题中具有启迪思维、搭建桥梁的重要作用，正如波利亚所说：“类比是一个伟大的引路人.”

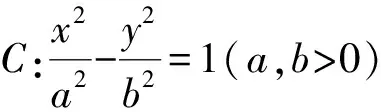
猜想4 抛物线C:y2=2px(p>0)的焦点为F，准线交x轴于点N(准点)，若AB为垂直于x轴的一条动弦，则直线AF与BN的交点M必在抛物线C上．

在动弦不过焦点时，猜想3、4的逆命题也成立．其证明同猜想1、2，留给读者完成．