一道三角形试题的多角度思考
2022-10-10江苏省南京市第九中学210018竺宝林
中学数学研究(江西) 2022年10期
江苏省南京市第九中学 (210018) 竺宝林
1.问题呈现

图1

2.问题分析
G·波利亚在《怎样解题》一书中提出:“寻求有用的思路,首先是我们应该从哪里开始,然后是我能做什么,即寻找你过去所学的知识之间的联系.”学生在遇到新问题时,要联想有没有遇到过这个问题,有没有遇到过类似的题目,有没有遇到过与这个问题相关的知识与方法.数学思路寻求关键是基于已有的认知结构进行思维联想.基于此,我们可以做以下联想:

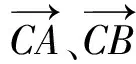

图2
3.问题解决
思路一:向量视角
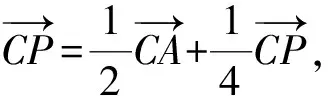


图3
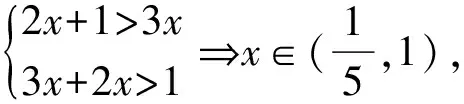
思路二:坐标视角

图4
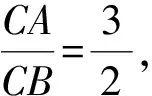
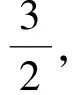

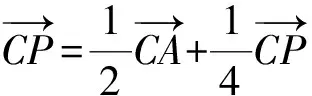

图5
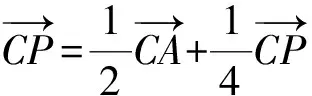
思路三:解三角形视角
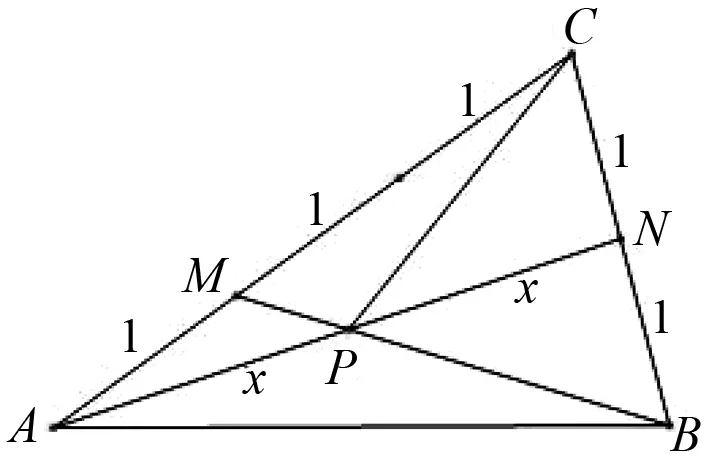
图6

4.解题思考
多视角思考,是指对同一个问题从不同角度来审视,以不同的切入点探求不同的解决方案.这样做,不仅能梳理解决此类问题的一般方法,揭示问题的内在本质和一般规律,而且能开拓思维,积累解题经验,激发学习兴趣,还能沟通知识间的联系,理清知识的脉络,构建完整的知识体系,更能优化思维品质,学会数学的思考.
对于一道有思维难度的问题,通过让学生联想知识点,联想方法与策略,可以帮助学生理清知识脉络、提升解题策略,并在以后解决难题的过程中,能够从容的进行方法策略联想,寻找解决问题的办法.因此,在解题教学中,要敢于让学生联想,放手让学生联想,解题思维过程是根据题目已有的信息联想自身存储的认知结构,提取相关的知识与方法,进行综合余取舍,探索出合理的解题思路的过程.
