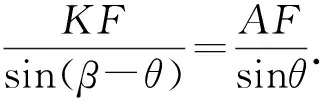探究一道以抛物线为背景的角度问题

重庆实验外国语学校 (400039) 李小燕

一、试题与分析

已知抛物线C:y2=2px(p>0)的焦点为F，准线l交x轴于点K，过F作倾斜角为α的直线与C交于A，B两点，若∠AKB=60°，求sinα的值.(佛山市2021届高三一模15题)

分析：本题有一个隐藏考点，射线Kx为∠AKB的角平分线(即kKA+kKB=0).其次则是研究sinα与∠AKB的关系.其中关于隐藏考点，在2015年全国Ⅰ卷的第20题中便考过类似的性质，该题目为：

对比可以发现模拟题中的结论更加特殊化，而2015年的试题更具一般性.

二、解法呈现

现将原问题分解成两个步骤完成，一是隐含的考点，即kKA+kKB=0；二是sinα与∠AKB的关系.关于第1个考点，解法如下：

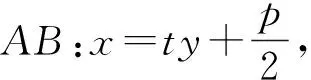
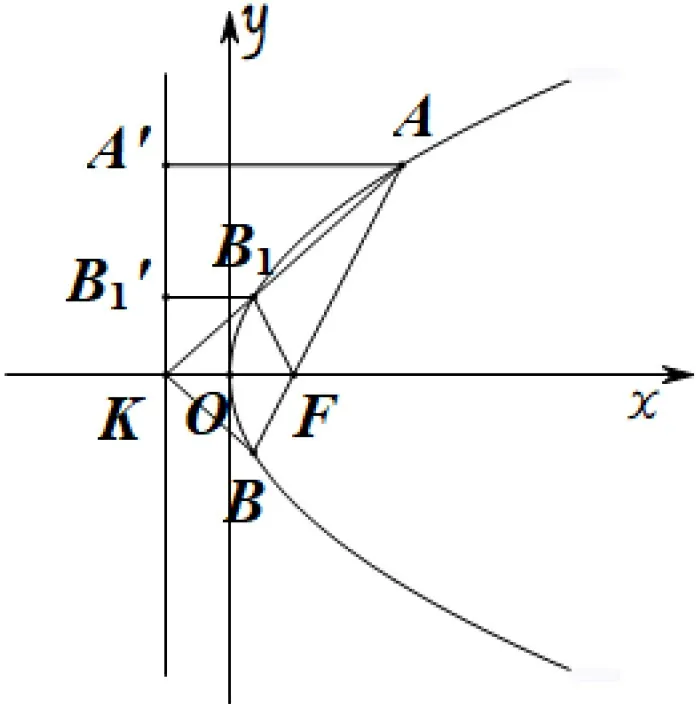
图1

如何利用该方式进行一般化证明呢？上述问题的一般化形式为：已知抛物线C:y2=2px(p>0)，直线l:x=-a交x轴于点K，过P(a,0)作倾斜角为α的直线与C交于A，B两点，则有射线Kx轴为∠AKB的角平分线(该问题即为2015年试题，仅抛物线的开口方向不同).

为了解决该问题，本文先介绍一下极点极线[1]的相关定义及性质.

极点极线的几何定义[2]点P是不在圆锥曲线上的点，过点P引两条割线依次交圆锥曲线于四点E,F,G,H，连接EH，FG交于N，连接EG，FH交于M，则直线MN为点P对应的极线.

图2

图3

该方法可直接迁移至其他圆锥曲线，例如2018年全国Ⅰ卷第19题[4]便是该性质在椭圆中的应用.

图4

三、变式拓展

根据上述的分析，对于一般的极点与极线都有相关的结论.为此，现将原问题作如下变形：

图5