充分挖掘教材习题的教学价值
——以人教版选择性必修一的一道习题为例
2022-10-10广东省佛山市顺德区杏坛中学528325陈美茹
广东省佛山市顺德区杏坛中学 (528325) 陈美茹
1.题目展示
(选择性必修第一册习题2.5的拓广探究第15题)已知点P(-2,-3)和以Q为圆心的圆(x-4)2+(y-2)2=9.
(1)画出以PQ为直径,Q′为圆心的圆,再求出圆Q′的方程;
(2)设圆Q与圆Q′相交于A,B两点,直线PA,PB是圆Q的切线吗?为什么?
(3)求直线AB的方程.
2.题目的背景及考查目标
(1)题目的基本背景
①圆的概念与标准方程;
②圆周角定理的推论:圆的直径所对的圆周角等于90°及切线的判定定理;
③几何公理:平面内过两点有且只有一条直线.
(2)题目的主要考查目标
①知识点:圆的标准方程、直线与圆的位置关系;
②思想方法:数形结合、转化与化归、坐标法等;
③能力:运算、推理论证、分析问题和解决问题能力.
3.题目的解题思路
第(1)问的分析:求圆Q′的方程,就得考虑求它的圆心与直径.结合已知条件条件,可利用P、Q两点的坐标求圆心Q′和直径,而Q的坐标由圆Q的方程可得.

图1
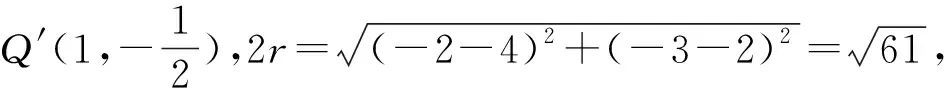
解题关键点:把求圆Q′的方程问题转化为求圆心Q′和直径,可利用相关几何特征轻易突破.
第(2)问的分析:如何判断是否切线,一般思路有:一是圆心到直线距离是否相等(从数的角度);二是直线是否符合平面几何的切线判定定理(从形的角度).而根据条件A、B是圆Q、Q′的公共点且PQ是圆Q′的直径,可以得到PA⊥AQ、PB⊥BQ,于是符合切线判定定理,问题解决.
(2)PA,PB是以Q为圆心的圆的切线.因为点A、B在圆Q:x2+y2-2x+y-14=0上,且PQ是圆Q′的直径,所以PA⊥AQ、PB⊥BQ.所以PA,PB是以Q为圆心的圆的切线.
解题关键点:挖掘条件中隐含着PA⊥AQ、PB⊥BQ,并通过数形结合,转化为A、B与圆Q、Q′的关系.
第(3)问的分析:求直线AB的方程,就得考虑与A、B有关数量条件:由已知A、B是圆Q、Q′的公共点,因此可转化为数量关系(即坐标关系):两点坐标是两圆方程的公共解,也就是两圆方程相减所得一次方程的解;联系到两点确定一条直线这一几何公理,得出结论.
(3)A、B是圆Q、Q′的公共点,则其坐标是(x-4)2+(y-2)2=9与x2+y2-2x+y-14=0的公共解,两方程相减并化简得6x+5y-25=0,即A、B在直线6x+5y-25=0上.又两点确定一条直线,则直线AB:6x+5y-25=0.
解题关键点:把A、B的几何特征转化为数量关系;可通过把握几何图形上的点与对应方程的解之间关系突破.
4.题目求解的思想方法
(1)找出条件和结论之间的联系,实现条件与结论的转化;
(2)利用数形结合,实现题目中的数量关系(即坐标关系)与几何特征的互化;
(3)利用转化与化归,把A、B的几何特征转化为两圆方程的公共解问题,从而解决问题.
5.题目的推广
为挖掘这一教材习题的教学价值,可对其做如下变式,从而引导学生从“变”发现“不变”的解析几何本质,从“不变”的本质中探究“变”的规律.
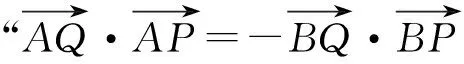
意图:通过变换问题表征,引导学生体验不同数学语言表征背后的相同数学本质.
(2)改变探求方向,延伸特征研究.如第(1)问改为“求出与圆Q:(x-4)2+(y-2)2=9关于P(-2,-3)对称的圆的方程”,或者改为“若Q′为圆Q:(x-4)2+(y-2)2=9上动点,求线段PQ′中点M的轨迹方程”;又如第(3)问改为“求弦长|AB|及△PAB的面积”等.
意图: 通过延伸特征研究,引导学生进一步体验利用数形结合思想与坐标法研究几何问题.
(3)转换问题背景,实现方法迁移.如把题目改为:“已知点P(-1,-1)和以Q为圆心的圆(x-1)2+(y-1)2=9,过P作出圆Q的切线,两个切点为A,B,求直线AB的方程.”
意图:引导学生再次经历直线与圆的关系问题可转化为两圆相交问题这一过程,强化转化、数形结合的思想.
(4)变静为动,加深数学理解.如把题目改为:“已知点P(-2,-3)和以Q为圆心的圆(x-4)2+(y-2)2=9,过P点的直线l与圆Q有交点,求直线l的斜率k的取值范围.”或者根据原题中直线PQ:5x-6y-8=0,把题目改为:“已知点P(a,b)在直线5x-6y-8=0上,圆Q:(x-4)2+(y-2)2=9,试根据a的范围讨论以PQ为直径的圆与圆Q的位置关系”等.
意图:通过变静为动,提高学生对解析几何的理解,渗透运动思想.
总之,习题教学是数学课的主要环节,它的有效性决定着教学目标落实的程度.认真剖析教材习题,从多角度挖掘其教学价值,这样不仅能加深学生对数学概念、定理等基础知识的理解和掌握,还能让学生在解题的准确性、灵活性和敏捷性上得到有效的提高.
