中考数学应用性问题的解题关键

福建省泉州市泉港区圭峰中学（362802）郭淑华

应用性问题是近几年中考数学的热点之一，它以解决实际问题为目标。要想破解应用性问题，需找到其解题关键。下面笔者结合近几年各地中考数学试题，分析应用性问题的特点，找出其解题关键，以供参考。

一、方程（组）的应用性问题

该类问题常见的类型有：（1）行程问题（包括相遇问题、追及问题、环形问题、水中航行问题等）；（2）工程问题；（3）浓度问题；（4）增长率或降低率问题；（5）数字问题；（6）最优策略问题；（7）最值问题。

［例1］（2021·张家界）2021 年是中国共产党建党100 周年，全国各地积极开展“弘扬红色文化，重走长征路”主题教育学习活动，我市“红二方面军长征出发地纪念馆”成为重要的活动基地。据了解，今年3 月份该基地接待参观人数10 万人，5 月份接待参观人数增加到12.1万人。

（1）求这两个月参观人数的月平均增长率；

（2）按照这个增长率，预计6 月份的参观人数是多少？

简析（1）设这两个月参观人数的月平均增长率为x，根据5 月份该基地接待参观人数=3 月份该基地接待参观人数×（1+增长率）2，即可得出关于x的一元二次方程，解之取其正值即可得出答案；（2）利用6 月份该基地接待参观人数=5 月份该基地接待参观人数×（1+增长率），即可求出答案。

点评列方程（组）解应用题，关键是认真审题，正确分析题意，找出问题中的等量关系，然后根据等量关系列出方程（组）。列方程（组）时，等式两边应意义相同、单位一致、数量相等。若所列的方程是分式方程，结果要验根并且所得的解与实际要相符合。

二、不等式（组）的应用性问题

该类问题常见的类型有：（1）以市场经济为背景的不等式（组）应用题；（2）运用不等式（组）解决的方案设计类应用题。

［例2］（2018·湘潭）湘潭市继2017年成功创建全国文明城市之后，又准备争创全国卫生城市。某小区积极响应，决定在小区内安装垃圾分类的温馨提示牌和垃圾箱，若购买2 个温馨提示牌和3 个垃圾箱共需550 元，且垃圾箱的单价是温馨提示牌单价的3倍。

（1）求温馨提示牌和垃圾箱的单价各是多少元？

（2）该小区至少需要安放48 个垃圾箱，如果购买温馨提示牌和垃圾箱共100 个，且费用不超过10 000 元，请你列举出所有购买方案，并指出哪种方案所需资金最少？最少是多少元？

简析（1）2 个温馨提示牌和3 个垃圾箱的总价格是550 元，垃圾箱的单价是温馨提示牌单价的3 倍，据此建立方程组即可得出答案；（2）根据“至少需要安放48 个垃圾箱”“费用不超过10 000 元”这两个信息，建立不等式组即可得出答案。

点评列不等式（组）解应用题的一般步骤是：（1）弄清题意和题目中的数量关系，用字母表示未知数；（2）找出能够表示题目全部含义的一个或几个不等式；（3）列出不等式（组），解不等式（组），求出解集并作答。解决这类问题的关键是根据问题实际建立不等式（组）模型，利用不等式（组）解的情况对问题作出最佳决策。

三、函数的应用性问题

该类问题常见的类型有：（1）一次函数的应用性问题；（2）二次函数的应用性问题；（3）分段函数及其他函数的应用性问题。

［例3］（2021·金华）某游乐场的圆形喷水池中心O有一雕塑OA，从A点向四周喷水，喷出的水柱为抛物线，且形状相同。如图1，以水平方向为x轴，点O为原点建立直角坐标系，点A在y轴上，x轴上的点C，D为水柱的落水点，水柱所在抛物线（第一象限部分）的函数表达式为

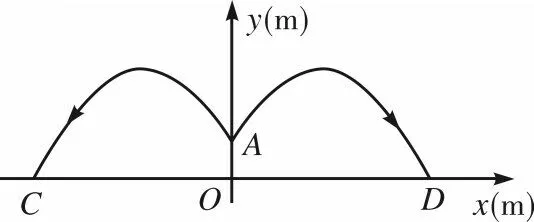
图1

（1）求雕塑高OA；

（2）求落水点C，D之间的距离；

（3）若需要在OD上的点E处竖立雕塑EF，OE=10 m，EF=1.8 m，EF⊥OD。问：顶部F是否会碰到水柱？请通过计算说明。

简析（1）利用二次函数图像上点的坐标特征可求出点A的坐标，进而得出雕塑高OA的值；（2）利用二次函数图像上点的坐标特征，求出点D的坐标，可得出OD的长度，由喷出的水柱为抛物线且形状相同，可得出OC的长度，再由CD=OC+OD即可求出落水点C，D之间的距离；（3）代入x=10 求出y值，进而可得出点在抛物线y=上，将与1.8 比较后即可得出顶部F不会碰到水柱。

点评利用函数模型来解决实际问题，首先要求出函数的解析式和自变量的取值范围，然后通过函数的增减性来确定函数的最值。

四、统计初步的应用性问题

统计初步有关问题是初中数学应用性问题的一个方面。随着素质教育对学生应用数学的意识要求的提高，近几年在中考数学试题中经常出现统计初步的应用性问题，教师在中考总复习时应重视。

［例4］（2019·鄂州）某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机选取该校部分学生进行调查，要求每名学生从中选出一类最喜爱的电视节目，以下是根据调查结果绘制的统计图表的一部分。（如下表和图2所示）

图2

请你根据以上信息，回答下列问题：

（1）统计表中m的值为______，统计图中n的值为______，A类对应扇形的圆心角为______度；

（2）该校共有1500 名学生，根据调查结果，估计该校最喜爱体育节目的学生人数；

（3）样本数据中最喜爱戏曲节目的有4 人，其中仅有1 名男生。从这4 人中任选2 名同学去观赏戏曲表演，请用树状图或列表求所选2 名同学中有男生的概率。

简析（1）由B 类别人数及其百分比求出调查人数，再用调查人数减去A、B、C、E 类别总人数得出m的值，然后根据百分比概念求出n，最后用360°乘以A 类别人数所占比例，获得圆心角的度数；（2）根据统计图表中的样本数据来估计，答案可得；（3）利用树状图或列表，将所有等可能的结果列举出来，利用概率公式求解即可。

点评解这类问题的关键是运用统计的思想对数据进行耐心、细致的观察，通过分析、比较，得到相应的特征数，运用统计初步的有关知识解决问题。

五、几何应用性问题

该类问题常见的类型有：（1）利用全等、相似及解直角三角形等知识进行测量的问题；（2）利用等腰三角形、圆、直角三角形等知识解决航海、气象等方面的问题。

［例5］（2020·聊城）如图3，小莹在数学综合实践活动中，利用所学的数学知识对某小区居民楼AB的高度进行测量。先测得居民楼AB与CD之间的距离AC为35 m，后站在M点处测得居民楼CD的顶端D的仰角为45°，居民楼AB的顶端B的仰角为55°，已知居民楼CD的高度为16.6 m，小莹的观测点N距地面1.6 m。求居民楼AB的高度（精确到1 m）。（参考数据：sin 55° ≈0.82，cos 55° ≈0.57，tan 55°≈1.43）

图3

简析过点N作EF∥AC交AB于点E，交CD于点F，通过解Rt△DFN得到线段NF的长度，进而得到线段NE的长度，再解Rt△BEN得到BE的长度。

点评解这类问题的关键是准确理解一些专有术语（如仰角、俯角、坡角、坡比、方位角、海拔等）的含义，在理解题意的基础上准确画出图形，把题目中的已知量和未知量转化到图形中，然后运用相应的几何知识来解决问题。

六、综合应用性问题

对应用性问题的考查，是近年中考数学的一大热点，有些试题同时考查多种应用性问题，要综合利用多种模型和各种知识才能解决。

［例6］（2018·南充）某销售商准备在南充采购一批丝绸，经调查，用10 000 元采购A 型丝绸的件数与用8 000 元采购B 型丝绸的件数相等，一件A型丝绸进价比一件B型丝绸进价多100元。

（1）求一件A型、B型丝绸的进价分别为多少元？

（2）若销售商购进A 型、B 型丝绸共50件，其中A 型的件数不大于B 型的件数，且不少于16 件，设购进A型丝绸m件。

①求m的取值范围；

②已知A 型的售价是800 元/件，销售成本为2n元/件；B 型的售价为600元/件，销售成本为n元/件。如果50 ≤n≤150，求销售这批丝绸的最大利润w（元）与n（元）的函数关系式（每件销售利润=售价-进价-销售成本）。

简析（1）根据题意，用分式方程解题；（2）①根据所提供条件，列出关于m的不等式组，可求得m的取值范围；②根据题意，列出销售利润y与m的函数关系式，讨论所含字母n的取值范围，则w与n的函数关系式可得。

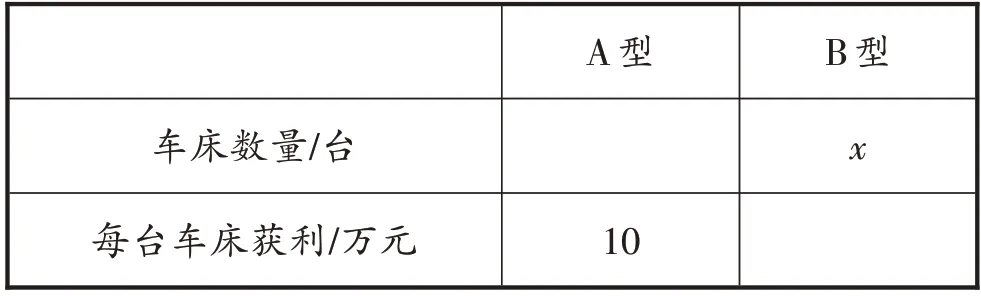
［例7］（2021·盘锦）某工厂生产并销售A，B 两种型号车床共14台，生产并销售1台A 型车床可以获利10 万元；如果生产并销售不超过4 台B 型车床，则每台B 型车床可以获利17 万元，如果超出4台B型车床，则每超出1台，每台B型车床获利将均减少1万元。设生产并销售B型车床x台。

（1）当x＞4时，完成以下两个问题：

①请补全下面的表格：

②若生产并销售B 型车床比生产并销售A 型车床获得的利润多70 万元，问：生产并销售B 型车床多少台？

（2）当0 ＜x≤14 时，设生产并销售A，B 两种型号车床获得的总利润为W万元，如何分配生产并销售A，B 两种车床的数量，使获得的总利润W最大？并求出最大利润。

简析（1）①由题意知，生产并销售B 型车床x台时，生产并销售A 型车床(14 -x)台，当x＞4时，每台B型车床可以获利[17 -(x-4)]=(21 -x)万元，②由题意得方程10(14 -x)+70=[17 -(x-4)]x，解得x1=10，x2=21（舍去）；（2）当0 ＜x≤4时，W=10(14-x)+17x，整理得W=3x+140，因为3 ＞0，故当x=4 时总利润W最大，为3×4 +140=152（万元）；当x＞4 时，W=10(14 -x) +[17 -(x-4) ]x，整理得W=-x2+11x+140，因为-1 ＜0，所以当x==5.5 时总利润W最大，又由题意知x只能取整数，所以当x=5或x=6时，总利润W最大，为-52+11 × 5+140=170（万元）。

点评综合应用性问题在突出综合性的同时强调应用性，这类问题一般注意联系学生的生活实际，关注社会热点，注重学科知识的内在联系和整合，能够有效考查学生收集信息和处理信息的能力、模型转化能力、分析综合能力、计算和表达的能力。解决这类问题的关键是根据题目的已知条件，分析数量关系，灵活运用分析法或综合法把隐蔽的“中间问题”找出来，迅速地找到解题的切入点，建立相关的数学模型。

纵观近几年来全国各地的中考数学试题，通过归类分析可知，应用性问题的解题关键是：在准确理解题意的基础上，利用已知条件，运用方程（组）、不等式（组）、函数、统计初步、几何等数学知识，分析实际问题中内在的、本质的关系，建立数学模型解决问题。