曲线折痕折纸力学超材料可定制压缩力学特性
2022-10-09刘杰徐依璐陈高锡文桂林薛亮李志勇
刘杰, 徐依璐, 陈高锡, 文桂林, 薛亮, 李志勇
(1.广州大学 机械与电气工程学院,广东 广州 510006; 2.燕山大学 机械工程学院,河北 秦皇岛 066004; 3.湖南大学 机械与运载工程学院,湖南 长沙 410082)
数学、力学、材料等学科引入到传统折纸工艺, 使折纸结构拥有自然界中普通材料不具备的物理性质,形成了折纸力学超材料,在定制力学特性、传热、隔声等领域得到了广泛的关注[1-3]。通过设计二维折痕图并在预定折痕处次序折叠,并结合几何衍化和堆叠等手段,折纸力学超材料可以实现各种各样的优越力学性能,如负泊松比、可编程模量、可定制刚度等。如,Schenk等[4]发现经典的三浦折纸结构具有面内负泊松比和面外正泊松比的非常规力学性能。Silverberg等[5]通过引入晶格缺陷实现了三浦折纸力学超材料模量的可编程特性。基于折痕重分配和堆叠策略,Wen等[6]提出了一种可定制多级刚度的折纸力学超材料。此外,薄壁管状折纸力学超材料在航空航天、汽车等领域的承载、能量吸收和隔振等方面展现出了巨大的潜力[7-9]。Wu等[10]研究了三浦折纸管在自由展开过程中的瞬态动力学行为。在此基础上,Han等[11]利用三浦折纸管实现了准零刚度特性,进而提出了一种非线性低频隔振器。Liu等[12]研究发现通过改变折叠角等参数可以大范围地调控三浦折纸管的动力学特性。除了三浦折纸管外,Agarwal等[13]还探讨了Kresling型管状折纸力学超材料在谐波力激励下的非线性动力学行为。
虽然上述基于直线折痕的折纸超材料已展现出了卓越的可定制力学特性,但两点之间只能有一条直线折痕但可以有多条曲线折痕。直线折痕大大减少了折纸力学超材料的设计自由度,进而限制了其可定制力学特性[14]。基于三浦折纸,Gattas等[15]提出了一种曲线折痕折纸结构建模方法。在此基础上,Zhai等[16]提出了一种曲线折痕折纸力学超材料,并证实了其在轻质机械爪、隔振和多级刚度响应等方面的应用潜力;利用碳纤维增强复合材料,Du等[17]设计了一种复合材料曲线折痕折纸超材料夹芯,并发现通过改变夹芯厚度可实现屈曲和破坏2种失效模式的定制。然而,目前很少有研究薄壁管状的曲线折痕折纸力学超材料,一定程度上限制了曲线折痕折纸力学超材料的实际工程应用潜能。
本文设计了一种曲线折痕圆柱折纸力学超材料,其二维基本单元由2条曲线谷折和一条曲线山折构成,曲线折痕使用二次函数表征。制备了曲线折痕圆柱折纸力学超材料样品,并研究了其制造精度。基于显式动力学数值仿真和物理试验法研究了曲线折痕圆柱折纸力学超材料压缩力学响应和变形模式,并探讨了曲线折痕对折纸力学超材料压缩力学特性的可定制性。
1 曲线折痕圆柱折纸力学超材料设计
1.1 基本单元设计策略
曲线折痕圆柱折纸力学超材料由预先设计的二维折痕图折叠而成,而二维折痕图的基本单元由2条曲线谷折和一条曲线山折组成。为了用数学语言定量地描述曲线折痕,选取二次函数定义山折和谷折的几何形状。需要指出,也可以使用其他的函数描述曲线折痕。又考虑到基本单元的几何对称性(如图1(a)的对称线),只需要使用函数描述基本单元的一半。如图1(a)所示,以基本单元右上角为原点,建立坐标系xOy,则曲线V和曲线M可分别描述为:
(1)
(2)
式中:w1和w2分别表示曲线M和曲线V波峰到x轴的距离;基本单元上下边界的长度为w;基本单元高度的一半设为2h。假设2条曲线谷折具有相同的几何形状,因此,远离x轴的曲线谷折可由曲线V沿着y轴平移w得到。
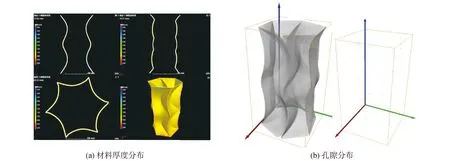
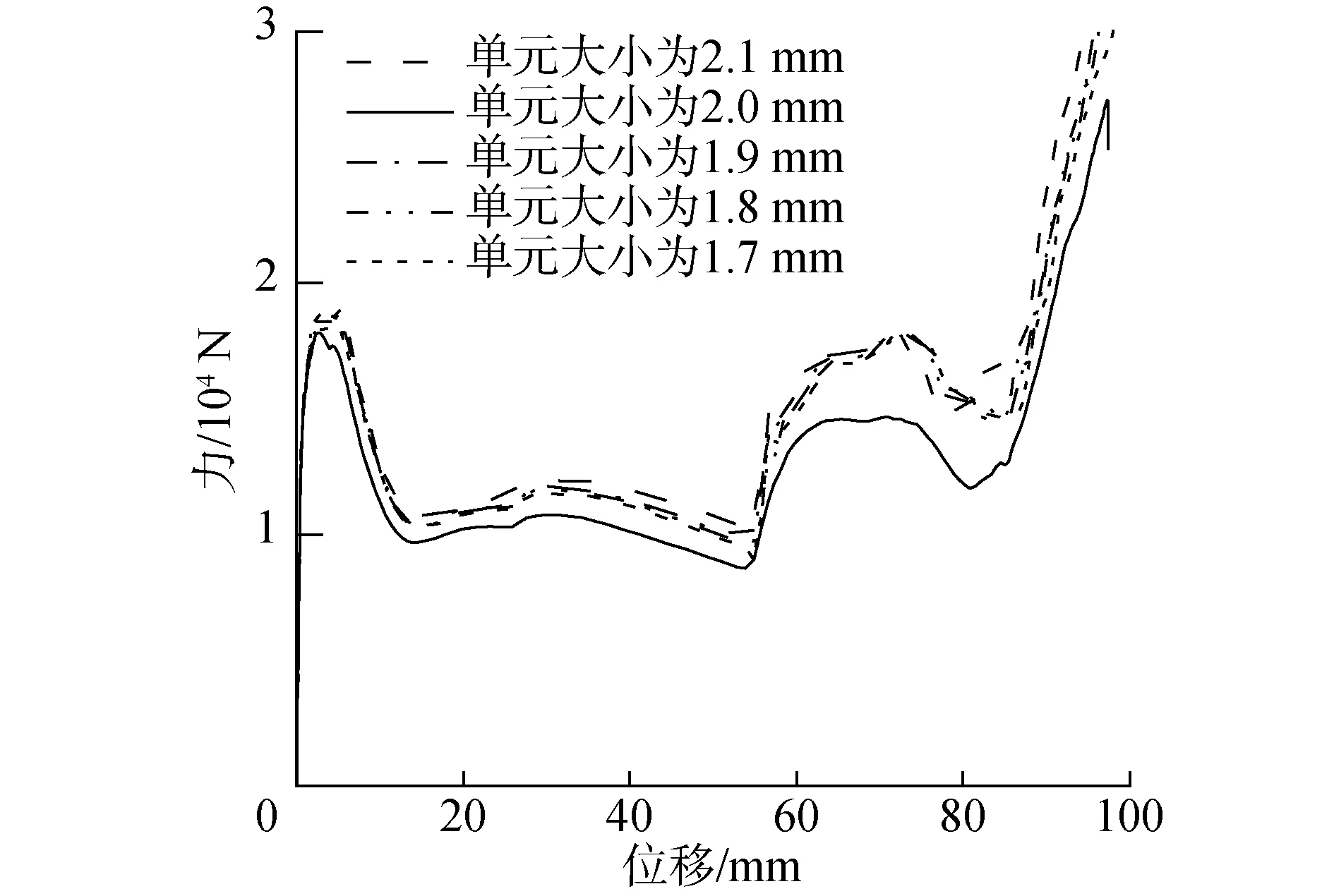
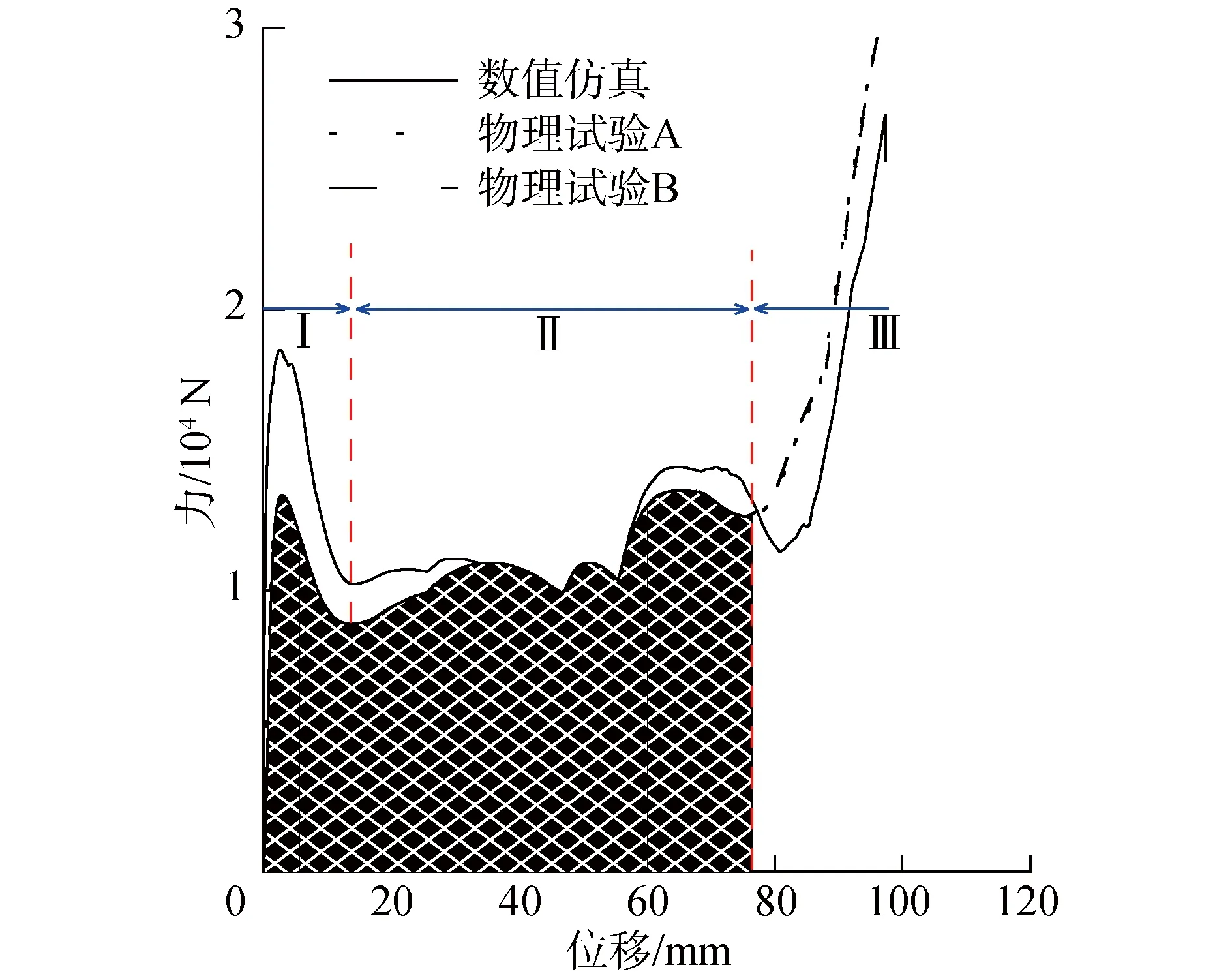
为了便于折叠和减缓折叠过程中中间部位的应力集中问题,对图1(a)所示的折痕图进行几何衍化,即,对曲线山折和曲线谷折在几何对称处进行圆角处理,如图1(b)所示。圆角半径假设为恒定值,且r1=2h/k1,r2=2h/k2,其中k1和k2分别取6.75和3.375(k1和k2也可以取其他数值)。此外,为了避免山折和谷折的相交且不改变它们的排列,令w1 图1 二维基本单元几何设计示意Fig.1 Geometric design for two-dimensional unit cell 将图1(b)所示二维基本单元折痕图分别在x轴和y轴方向上周期阵列,得到曲线折痕圆柱折纸力学超材料的二维折痕图。图2(a)给出一个典型的1×6二维折痕图,其中,Nx和Ny分别表示二维基本单元分别在x轴和y轴方向上周期阵列个数,W和H分别表示二维折痕图外边界的宽度和高度。对图2所示二维折痕图在折痕处次序折叠(图2b)并使边界线L和边界线R重合围成圆柱状,得到图2(c)所示的曲线折痕圆柱折纸力学超材料。本文主要研究1×6二维折痕图折叠而成的折纸力学超材料,但同样可以扩展到其他折痕图情况(即Nx和Ny取其他数值)。 图2 曲线折痕圆柱折纸力学超材料设计过程Fig.2 Design process of curved-creased cylindrical origami mechanical metamaterial 使用金属增材制造方法制备图2所示的折纸力学超材料,如图3所示。该折纸力学超材料的厚度为t=1 mm,基体材料为316L不锈钢,几何尺寸为:w1=10 mm,w2=30 mm,w=40 mm,r1=20 mm,r2=7.5 mm, 2h=67.5 mm。考虑到折纸力学超材料几何结构复杂且厚度较薄,使用三维CT扫描检测折纸力学超材料打印样品的质量,检测示意图如4所示。 图3 曲线折痕圆柱折纸力学超材料增材制造样品Fig.3 Additive manufacturing sample for the curved-creased cylindrical origami mechanical metamaterial 高精度三维CT扫描设备(型号:nanoVoxel-4000)最高分辨率为2 μm,微焦点封闭式反射靶X射线源发射X射线穿过折纸力学超材料,利用平板探测器检测信号。在检测过程中,将折纸力学材料进行360°旋转得到一系列二维图,并最终重构为三维图,如图5所示。图5(a)表明折纸力学超材料的大部分壁厚为1 mm左右,且波动较小;而通过图5(b)可知折纸力学超材料的孔隙率只有0.03%。因此,折纸力学超材料的打印质量较高,排除了样本制备对后续力学特性研究的影响。 图4 折纸力学超材料打印样品质量检测示意Fig.4 Schematic diagram of quality inspection of origami mechanical metamaterial print samples 316L不锈钢的材料属性由标准拉伸试验获得,如图6所示。图6(a)为拉伸试验设置图,标准试件安装于拉伸试验机(型号:LABSANS LD26.504)上下2个夹具中间,使用引伸计来测量试件的变形。图6(b)为316L不锈钢材料的工程应力-应变图。最后获得316L不锈钢的材料属性为:密度ρ=7 920 kg/m3,杨氏模量E=190.79 GPa,屈服应力σy=395.5 MPa,极限拉伸强度σu=629 MPa,极限拉伸强度σu=629 MPa,极限拉伸应变εu=42.455%,泊松比υ=0.3。材料采用弹塑性模型本构模型。 利用非线性有限元软件Abaqus/Explicit对折纸力学超材料轴向压缩力学特性进行了准静态数值仿真模拟,有限元模型如图7所示。 图5 折纸力学超材料CT扫描结果Fig.5 CT scan results for origami mechanical metamaterial 图6 316L不锈钢的材料拉伸试验Fig.6 Material tensile test of 316L stainless steel 图7 折纸力学超材料压缩力学显式动力学仿真有限元模型Fig.7 Compression mechanics explicit dynamics simulation finite element model of the origami mechanical metamaterial Explicit分析方法可有效求解准静态问题[6,18]。折纸力学超材料位于上刚性板和下刚性板之间,上下刚性板上的节点分别耦合到刚性板上的耦合点上,在上刚性板的耦合点上轴向施加位移载荷,实现轴向准静态压缩;在下刚性板的耦合点上施加固定约束。使用线性三角形(S3R)单元对折纸力学超材料进行有限元划分。位移载荷通过光滑时间步施加,在1 s内从0 mm增大到100 mm,可得平均速度为100 mm/s,对比文献[6,18],可认为准静态过程,且可忽略应力波的影响。采用库伦摩擦,摩擦系数为0.25,并采用硬接触来模拟表面间的接触压力。所有的模拟中都使用一般接触,并在模拟过程中考虑沙漏效应和动力学效应[18]。为了权衡有限元计算效率和精度,进行网格敏感性分析(见图8),确定全局网格大小约为2.0 mm。图8中所有模拟均在压缩量为100 mm收敛良好。为了解决显式动力学仿真过程中大规模计算量问题,所有的模拟均在超级计算平台(北京超级计算云计算中心)上并行64个CPU完成。 图8 网格灵敏度分析Fig.8 Mesh sensitivity analysis 设计物理试验来验证显式动力学数值仿真模型的有效性,物理试验的设置与有限元模型保持一致,如图9所示。将折纸力学超材料样安置在拉伸试验机(型号:Instron 5900)上下平板之间,在平板上加工便于安装样品的凹槽。拉伸试验机以2 mm/min的速度对折纸力学超材料样品进行轴向压缩,使用数码相机(型号:Canon ESO 77D)记录整个压缩过程,并利用带有数据处理系统的PC机进行数据处理。 图9 物理试验设置Fig.9 Physical test setup 图10和图11分别展示了折纸力学超材料显式动力学数值仿真和物理试验压缩力学响应和典型压缩过程。可以发现2种方法得到的结果基本一致,即,压缩力学响应曲线的趋势一致,且压缩过程中典型变形模式相同。值得注意的是,数值仿真得到的峰值力要大于物理试验,这是由于虽然金属增材制造得到的折纸力学超材料样品的质量较高,但不可避免存在一定的制造缺陷,而数值仿真模型是理想模型。此外,对2个折纸力学超材料样品分别做2次物理试验A和B,图10可看出2次物理试验的压缩力学响应基本重合,说明了样品质量的稳定性和物理试验方法的可靠性。进一步,图10的压缩力学响应曲线划分为3个阶段,即阶段Ⅰ、阶段Ⅱ和阶段Ⅲ。在阶段Ⅰ,折纸力学超材料整体向左扭转,主要变形模式为整体扭转,出现了整体压扭特性。当压缩量为约3 mm,出现峰值力;之后,折纸力学超材料出现明显的扭转,压缩量为约13 mm,折纸力学超材料出现全局失稳,此时力学响应最小。图11给出了一个典型的整体扭转变形模式(压缩量为12 mm)。在阶段Ⅱ,折纸力学超材料上、下部分面板同时开始弯曲,且存在面板内表面相互接触,致使力学响应存在一定的波动,具体的,压缩量从约13 mm到约35 mm,响应曲线缓慢上升到一个峰值,然后逐渐降低到一个谷值(压缩量约为54 mm),接着力学响应急剧增大到一个最大值,这是由于面板之间的相互接触导致。整个压缩阶段Ⅱ可认为应力平台阶段,该阶段折纸力学超材料的变形模式以面板弯曲为主(图11展示的压缩量为50 mm的变形模式)。阶段Ⅲ为折纸力学超材料整体压实阶段,图11展示了压缩量为95 mm折纸力学超材料的变形图。可见,在轴向压缩过程中,折纸力学超材料的主要变形模式为“整体扭转”→“面板弯曲”。从物理试验结果可见,峰值力相对于平台区力响应数值相差不大,且力学响应曲线有效吸能区域面积很大(图10阴影部分),因此,该曲线折痕圆柱折纸力学超材料具有良好的缓冲和吸能特性。 图10 折纸力学超材料显式动力学仿真和物理试验压缩力学响应Fig.10 Compressive mechanical response of explicit dynamics simulation and physical tests for the origami mechanical metamaterial 图11 折纸力学超材料显式动力学仿真和物理试验压缩过程Fig.11 Compression process of explicit dynamics simulation and physical tests for the origami mechanical metamaterial 在基本单元二维折痕图上改变曲线山折和曲线谷折的几何形状,探究其对曲线折痕圆柱折纸力学超材料压缩力学性能的影响,进一步揭示所提折纸力学超材料可定制力学性能,包括力学响应和变形模式。 通过方程(1)可知,改变w1的可改变曲线谷折的几何形状,保持其他参数不变,分别取w1的值为5、7、10、12和15 mm,探究曲线谷折对折纸力学超材料压缩力学性能影响。图12给出了折纸力学超材料在不同曲线谷折下的压缩力学响应曲线,可见曲线谷折对折纸力学超材料的压缩力学响应具有很大的影响,包括峰值力和曲线变化规律。当w1从5 mm增大到7 mm再增大到10 mm时,力学响应曲线具有类似的变化趋势,即均存在2.2节所述的阶段Ⅰ、阶段Ⅱ和阶段Ⅲ 3个变形阶段。主要变形模式均为“整体扭转”→“面板弯曲”,与图11类似。而当w1从10 mm继续增大到12 mm和15 mm时,折纸力学超材料的压缩力学响应在数值和趋势上均发生了变化,其变形模式也发生了变化,特别在压缩量为50 mm左右会出现一个明显的波峰。折纸力学超材料上半部分先局部向右扭转,然后上半部分发生面板弯曲,然后下半部分向右局部扭转,接着下半部分面板弯曲,最后整体压实。因此,其主要变形模式为“上半部分扭转”→“上半部分面板弯曲”→“下半部分扭转”→“下半部分面板弯曲”,如图13所示。 图12 折纸力学超材料在不同曲线谷折下的压缩力学响应曲线Fig.12 The compressive response curves of the origami mechanical metamaterial under different curved valley creases 图13 折纸力学超材料在w1为12 mm和15 mm的变形模式Fig.13 Deformation modes of origami mechanical metamaterials when w1 equals 12 mm or 15 mm 此外,相比w1=10 mm和w1= 15 mm的情况,当w1=12 mm时,力学超材料在加载初段出现的第一次峰值力明显高很多。这是由于w1=12 mm时力学超材料上半部分的扭转刚度很大,且在加载初段主要变形模式为上半部分扭转。由此可见,当描述基本单元折痕图的其他参数保持不变,w1越小,折纸力学超材料压缩过程中的主要变形模式为“整体扭转”→“面板弯曲”;而w1越大,折纸力学超材料压缩过程中的主要变形模式为“上半部分扭转”→“上半部分面板弯曲”→“下半部分扭转”→“下半部分面板弯曲”。此外,当w1取值7 mm时,折纸力学超材料在平台段的承载性能更好。可通过对w1进行优化设计,以实现更好的缓冲和吸能特性。因此,单纯改变曲线谷折可以很好地实现对折纸力学超材料进行压缩力学特性的定制。 通过方程(2)可知,改变w2的可改变曲线山折的几何形状,保持其他参数不变,分别取w2的值为25,27,30,32和35 mm,研究曲线山折对折纸力学超材料压缩力学性能影响。图14给出了折纸力学超材料在不同曲线山折下的压缩力学响应曲线,可以发现曲线山折对峰值力的影响较小(第1峰值力均在18 kN左右),但对力学响应曲线的变化规律影响很大。当w2取值25 mm和27 mm时,折纸力学超材料的变形模式为“上半部分扭转”→“上半部分面板弯曲”→“下半部分扭转”→“下半部分面板弯曲”,如图11所示;而当w2取值30、32和35 mm时,折纸力学超材料的变形模式为“整体扭转”→“面板弯曲”(如图13所示)。w2=35 mm的折纸力学超材料出现2个明显峰值力,且第2个峰值力很高,比第1个峰值高接近5 kN(压缩量约50 mm),这是由于折纸超材料中间部位出现面板“鼓起”现象(见图14右下角),此时面板内表面发生相互接触,致使力迅速增大;当压缩量从50 mm继续增大,折纸力学超材料出现局部失稳,响应曲线瞬间下降。对比5种折纸力学超材料,w2取值35 mm时具有更好的吸能性能。 通过方程(1)和方程(2)改变曲线谷折和曲线山折的几何形状可以实现折纸力学超材料压缩力学性能大范围的调控。改变曲线谷折(w1)对折纸力学超材料响应曲线影响更大,这是由于曲线谷折的改变影响了二维基本单元的面积,进而影响了折纸力学超材料的质量;而改变曲线山折(w2)不会影响折纸力学超材料的质量,但当w2足够大(接近w)时,折纸力学超材料会出现面板内表面相互接触,致使在压缩量50 mm附近出现一个很大的幅值,这对缓冲性能是不利的。此外,当描述基本单元折痕图的其他参数保持不变,w1较小且w2较大时,折纸力学超材料压缩过程中的主要变形模式为“整体扭转”→“面板弯曲”,出现整体压扭现象;而w1较大且w2较小时,主要变形模式为“上半部分扭转”→“上半部分面板弯曲”→“下半部分扭转”→“下半部分面板弯曲”,出现局部压扭现象。这是由于当w1较小且w2较大时,曲线折痕圆柱折纸力学超材料中部扭转刚度较小,在受到轴向压缩时容易出现整体扭转失稳;而因当w1较大且w2较小时,曲线折痕圆柱折纸力学超材料中部扭转刚度较大,致使其上半部分和下半部分更容易出现局部扭转失稳。此外,基于直线折痕的折纸力学超材料的变形模式一般为“折痕转动”和“面板弯曲”[4], 且一般通过调整材料厚度来实现不同变形模式的定制[15]。而本文所提折纸力学超材料可以通过在基本单元二维折痕图上定制曲线折痕实现对曲线折痕圆柱折纸力学超材料压缩力学响应和变形模式的定制,且出现了更加丰富的变形模式。值得指出的是,相较于直线折痕折纸力学超材料,曲线折痕转动在力学超材料变形过程中并不起主导作用,但会伴随其他变形模式发生曲线折痕的转动。 图14 折纸力学超材料在不同曲线山折下的压缩力学响应曲线Fig.14 The compressive response curves of the origami mechanical metamaterial under different curved mountain creases 1)改变基本单元二维折痕图上的曲线山折和曲线谷折可实现曲线折痕圆柱折纸力学超材料压缩力学响应大范围的调控; 2)控制其他几何参数不变,调控w1和w2可实曲线折痕圆柱折纸力学超材料变形模式的转变,即,当w1较小且w2较大时,变形模式为“整体扭转”→“面板弯曲”(整体压扭特性),而当w1较大且w2较小时,变形模式变为“上半部分扭转”→“上半部分面板弯曲”→“下半部分扭转”→“下半部分面板弯曲”(局部压扭特性); 3)适当调控曲线山折和曲线谷折,可实现曲线折痕圆柱折纸力学超材料的较低压缩峰值力和较大有效吸能区域,因此,所提折纸力学超材料具有良好的缓冲和吸能特性。所提思路增加了折纸力学超材料的设计自由度,进而丰富了其可定制压缩力学特性。 本文通过试验和仿真手段定性地探索了曲线折痕圆柱折纸力学超材料可定制的丰富压缩力学特性,后续将尝试从能量角度对变形模式进行定量的解释。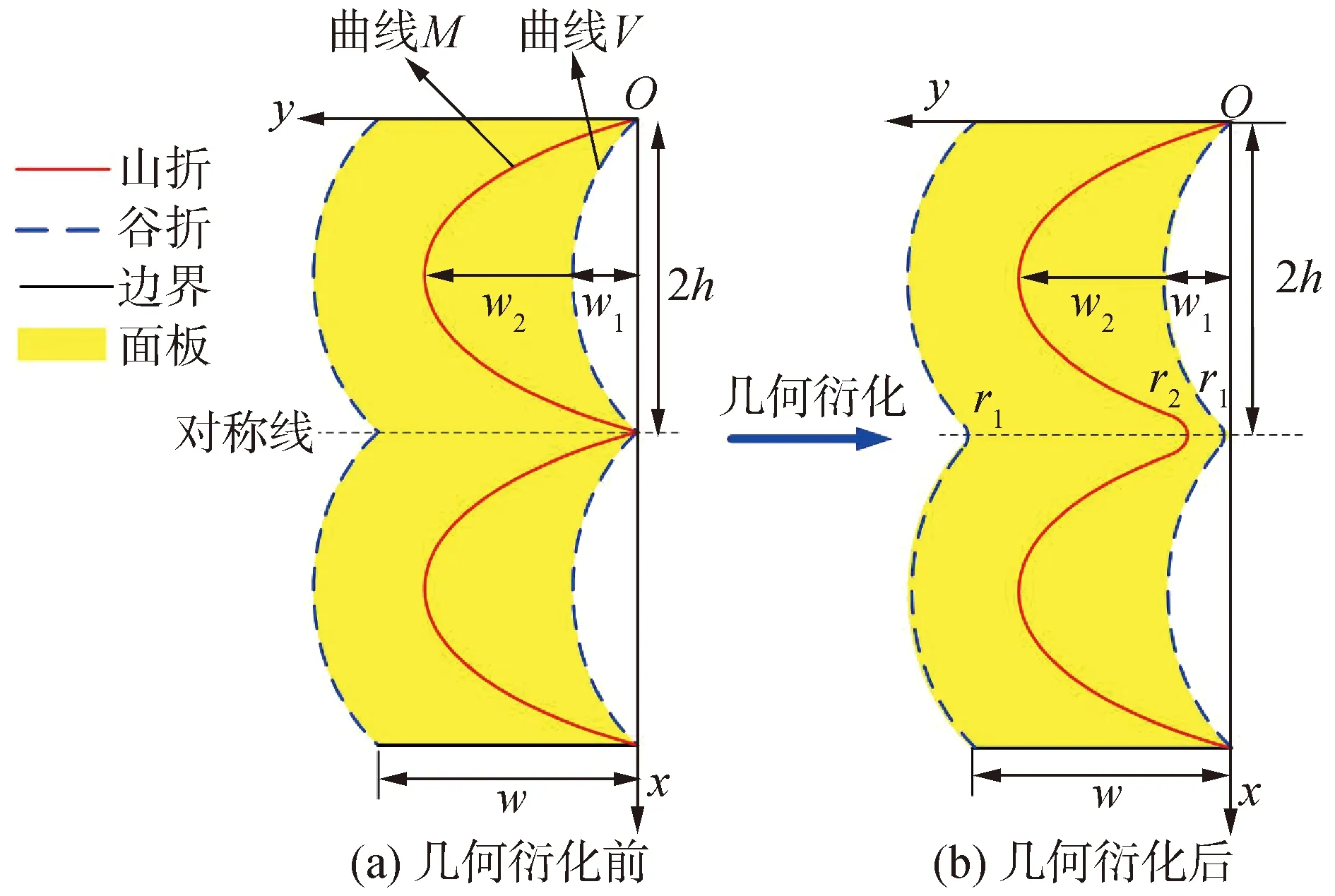
1.2 折纸力学超材料设计策略

2 曲线折痕圆柱折纸力学超材料力学性能分析
2.1 折纸力学超材料制备


2.2 折纸力学超材料力学性能分析




3 曲线折痕圆柱折纸力学超材料可定制压缩力学性能研究
3.1 曲线谷折对折纸力学超材料压缩力学性能影响


3.2 曲线山折对折纸力学超材料压缩力学性能影响
3.3 讨论

4 结论
