新型双稳态屈曲梁结构的低频跳跃稳定性分析
2022-10-09王胜杰韩翻珍郭翔鹰
王胜杰, 韩翻珍, 郭翔鹰
(1.北京工业大学 材料与制造学部, 北京 100124; 2.国家知识产权局专利局, 北京 100088)
双稳态结构具有2个稳定的平衡态,当外界输入载荷达到其跳跃突变所需的临界值时,将从一个稳定状态跳跃突变到另一个稳定的状态,从而实现能量的转移及消耗。双稳态可通过磁铁、弹簧、屈曲梁等结构产生,由于屈曲梁结构质量轻、体积小、适应性强,以及双稳态跳跃位移大等特性,受到学者们的广泛青睐,用在能量吸收和耗散的结构设计中[1-2],尤其在能量采集[3-4]、隔振[5-6]等机械装置[7-9]方面有了大量的研究报道。Vangbo[10]建立了一个理论模型来跟踪双夹紧预压屈曲梁在中心力作用下的快速跳变路径。赵和贾等[11-12]基于广义变分原理,借助半纯函数公式解析地给出了预压屈曲梁双稳态跳跃过程中横向力与位移间的非线性关系式。Camescasse等[13-14]对双稳态屈曲梁的跳变机制进行了实验验证,分析了梁受到中心载荷和偏心载荷作用下的力与位移的关系,研究了力的施加点对静态分叉的影响,并得到了分叉驱动力的最小值。Su等[15]研究了力矩输入驱动的双稳态屈曲梁,建立了理论模型预测必要的输入力矩,并进行了实验验证。肖和黄[16]对带有初始小挠度的两端固支屈曲梁进行研究,发现在初始小挠度屈曲下,梁的反对称模态并未被激发; 而随着外激励力的变化,系统会发生倍周期分岔和鞍结分岔,导致解的突变。Jin等[17]理论分析了石墨烯增强复合材料板后屈曲夹层梁的非线性弯曲和强迫振动,得到了不同轴向压缩条件下弯曲缺陷灵敏度和主共振特性。此外,还有一些学者通过设计不同的结构实现双稳态形式的快速跳变[18-19],用于振动能量的俘获和采集[20-21]。
目前双稳态结构大部分用于俘能装置的设计中,将双稳态结构应用于吸振装置方面报道比较少。本文主要探索新型双稳态屈曲梁结构跳变的最小势能阱,分析随着中间铰支约束位置变化时,双稳态屈曲梁发生跳变的最小力矩变化趋势。通过实验验证双稳态屈曲梁结构在低频外部激励下的跳变,并分析能产生良好跳变的频率范围。
1 新型双稳态屈曲梁理论模型
基于Euler-Bernoulli梁模型,考虑小挠度假设,建立如图1所示双稳态屈曲梁模型。考虑弹性简支边界条件,并在梁中间施加铰支约束,无外力作用时如图1(a)所示,梁原始长度为L0。沿x轴两端施加相同的轴向压力P,当压力大于其临界屈曲载荷时梁会发生屈曲,被压缩为L,被压缩长度为d0,轴向压缩比为η=d0/L0。在移动铰支处施加驱动力矩,诱导屈曲梁产生跳变。屈曲梁的2个稳定平衡状态如图1(b)Ⅰ位置和Ⅱ位置所示。

图1 双稳态屈曲梁的理论示意Fig.1 Schematic diagram of pre-compressed bistable buckling beam theory
根据Euler-Bernoulli梁模型,梁的抗弯刚度为EI,抗拉模量为EA,在轴向压力P作用下梁的控制方程为:
w(4)+n2w″=0
(1)
式中:w为梁的横向位移;n2=P/EI;E为杨氏模量;I为梁的惯性矩。
当x=xM时,简支梁的边界条件为:
(2)
将边界条件代入梁的控制方程(1)可得梁的振型函数为:
(3)
考虑驱动力矩对屈曲梁跳变的影响,屈曲梁在2个稳定状态间跳变表示为梁的不同阶屈曲模态的叠加:
(4)
首先,通过能量法来求解双稳态屈曲梁在2个稳态之间的跳跃突变行为,在轴向压力和外加力矩作用下,系统的总势量为:
U=Ub+Up+UM
(5)
式中Ub表示弯曲势能:
(6)
(7)
压缩势能由胡克定律给出,表示为:
(8)
驱动力矩所做的功表示为:
UM=-Mw′(xM)
(9)
当无中间铰支约束时,屈曲梁主要产生一阶屈曲,产生高阶屈曲比较困难且不稳定。本设计通过中间铰支约束,使简支屈曲梁能在一阶频率附近产生稳定的二阶屈曲双稳态构型,而其他阶屈曲模态对其跳变行为影响较小。此时,只需要取其一阶屈曲模态函数就足以表明梁的稳态跳变行为,其屈曲形状函数为:
(10)
将式(10)代入势能方程(5),即可求得系统的总势能。由于梁的平衡状态发生在势能最小的位置,因此必须求出最小势能的解a1,即求解
∂U/∂a1=0
(11)
这样求出a1的同时,得到相应屈曲函数w1(x)。然后将求解出来的a1代回方程(10)再结合梁长的约束方程,即可求得使双稳态屈曲梁跳跃突变的最小驱动力和移动铰支位置之间的关系式:
(12)
考虑移动铰支位置变化时,简支梁发生二阶屈曲的最小力矩变化情况,取正交铺设的碳纤维梁为研究对象,其中材料和结构参数如表1。

表1 梁的材料和尺寸参数Table1 Material and dimensional parameters of the beam
本文研究了驱动位置在0~L/2内,驱动力矩随驱动位置的变化情况,将表1材料参数代入方程(11)即可求出不同位置处梁发生跳变的最小驱动力矩,得到最小驱动力矩和驱动位置的之间的关系,如图2所示。

图2 最小驱动力矩与力矩作用位置的关系Fig.2 Critical actuation moment versus position of applied moment
图2中显示了在相同压缩条件下最小驱动力矩与驱动位置的关系,可以发现,当驱动位置接近梁的末端时,驱动力矩将会变得无穷大,当驱动位置接近梁的中点时,仅需要一个很小的驱动力矩就可以使屈曲梁发生跳变,此时的驱动力矩为0.26 N·m。
2 屈曲梁有限元仿真分析
通过有限元分析验证理论分析结果,建立图1所示的双稳态屈曲梁模型,其材料参数同表1相同。以xM=L/2位置为例,对施加铰支约束的弹性梁进行屈曲分析,首先对梁进行线性屈曲分析,得到弹性梁屈曲的临界屈曲载荷大小,求得临界屈曲载荷后,对梁施加预压轴向力(大于临界屈曲载荷)或者轴向位移,并在梁中点铰支处施加一个极小的初始转角,使弹性直梁发生屈曲,弹性梁后屈曲状态如图3所示。

图3 弹性梁后屈曲Fig.3 Post-buckling beam
接着对此屈曲梁进行模态分析,得到简支梁前三阶固有频率分别为11.429、127.07、390.42 Hz,得到前三阶模态振型如图4所示,发现在一阶固有频率附近能产生稳定的二阶屈曲双稳态构型,所以双稳态屈曲梁可以在较低频率范围内进行跳跃突变。
最后,基于上述模型,当铰支约束位置不同时,在铰支约束处施加较小的驱动力矩,模拟预压双稳态屈曲梁的跳转运动过程,使其从初始位置跳跃到另一个稳态位置,跳跃突变过程示意图如图5所示,发现在外部驱动力矩作用下,双稳态屈曲梁可以产生跳跃突变。此时施加的驱动力矩大小分别为0.309、0.291、0.274 N·m。
通过仿真可以发现,当移动铰支座移动到梁的中点时,所需要的驱动力矩最小,与理论计算结果基本一致。
3 双稳态屈曲梁跳跃突变实验
为了验证外力矩对新型双稳态屈曲梁结构稳定跳变的影响,设计如图6所示的实验装置,基于理论和仿真分析,以xM=L/2为例,建立如图5所示实验模型,其中由质量块和扭转机构提供屈曲梁跳跃突变的驱动力矩。

图4 前三阶模态振型Fig.4 The first three mode shapes
随着外部激励幅值的增加,当扭转机构吸收的能量大于双稳态屈曲梁的势能壁垒时,双稳态屈曲梁发生跳跃突变,屈曲梁从第一/第二稳定构型转变为第二/第一稳定构型。由于能量的突然释放,在2个稳态之间进行跳变时会引起屈曲梁的高频振动,从而将外部输入能量转变为稳态之间进行跳跃突变的能量。
为了进一步评估所提出的解析模型和有限元分析的可靠性,本文搭建了一个实验装置来验证屈曲梁的跳跃突变特性。如图7所示,将所建立的实验模型放置在型号JZK-5T的激振器上,信号输入系统由YE1311信号发生器和YE5874功率放大器组成,信号采集系统由计算机、信号采及分析仪和加速度传感器构成。
首先对设计的结构进行了扫频分析,发现在8~13、31和88 Hz附近有一个共振峰,说明在此频段附近结构与外激励频率发生了共振。为了观察屈曲梁在不同频率激励作用下的跳跃突变行为,通过激振器给所建实验模型施加不同频率的外部激励,观察屈曲梁在不同频率激励作用下的跳跃突变行为,并用加速度传感器来记录双稳态屈曲梁最高点在跳跃突变过程中的加速度变化,通过积分变换,得到屈曲梁最高点的位移变化历程。

图5 不同作用位置驱动力矩作用下的跳跃突变过程Fig.5 Snap through process under the concentrated moment
分别对频率范围为8~15 Hz,激励力幅值为2 vpp外部干扰下,双稳态屈曲梁最高点的加速度进行了采集分析,通过积分变换得到时间位移曲线如图8所示。
由上述时间位移图可以看出,新型双稳态屈曲梁结构在低于8 Hz和超过15 Hz外部激励下,并不会发生跳跃突变行为,只是做简单的微幅振动,而在9~14 Hz屈曲梁在扭转机构的带动下开始发生跳变,但在9~12 Hz时双稳态屈曲梁在反向跳变时会出现微弱的迟滞现象,是因为重力作用影响下,扭转机构在回到初始位置时,会有一部分能量耗散。因此可以在此频率区间内进行双稳态吸振结构的设计。在13~14 Hz时外激励频率与双稳态结构产生了共振,双稳态屈曲梁进行稳定的跳跃突变,在此频率区间内可进行俘能结构的设计。

图6 双稳态屈曲梁结构Fig.6 Bistable buckling beam structure

注:1.YE5874功率放大器,2.YE1311信号发生器,3.信号采及分析仪,4.计算机,5.加速度传感器,6.双稳态屈曲梁跳转机构,7.JZK-5T激振器图7 实验设备Fig.7 Experimental equipment
目前仅对xM=L/2位置下受驱动力矩的双稳态屈曲梁进行了实验验证,对于随着驱动力矩位置的改变,双稳态屈曲梁是否能够在更宽的低频范围内进行跳跃突变,仍需要进一步研究。
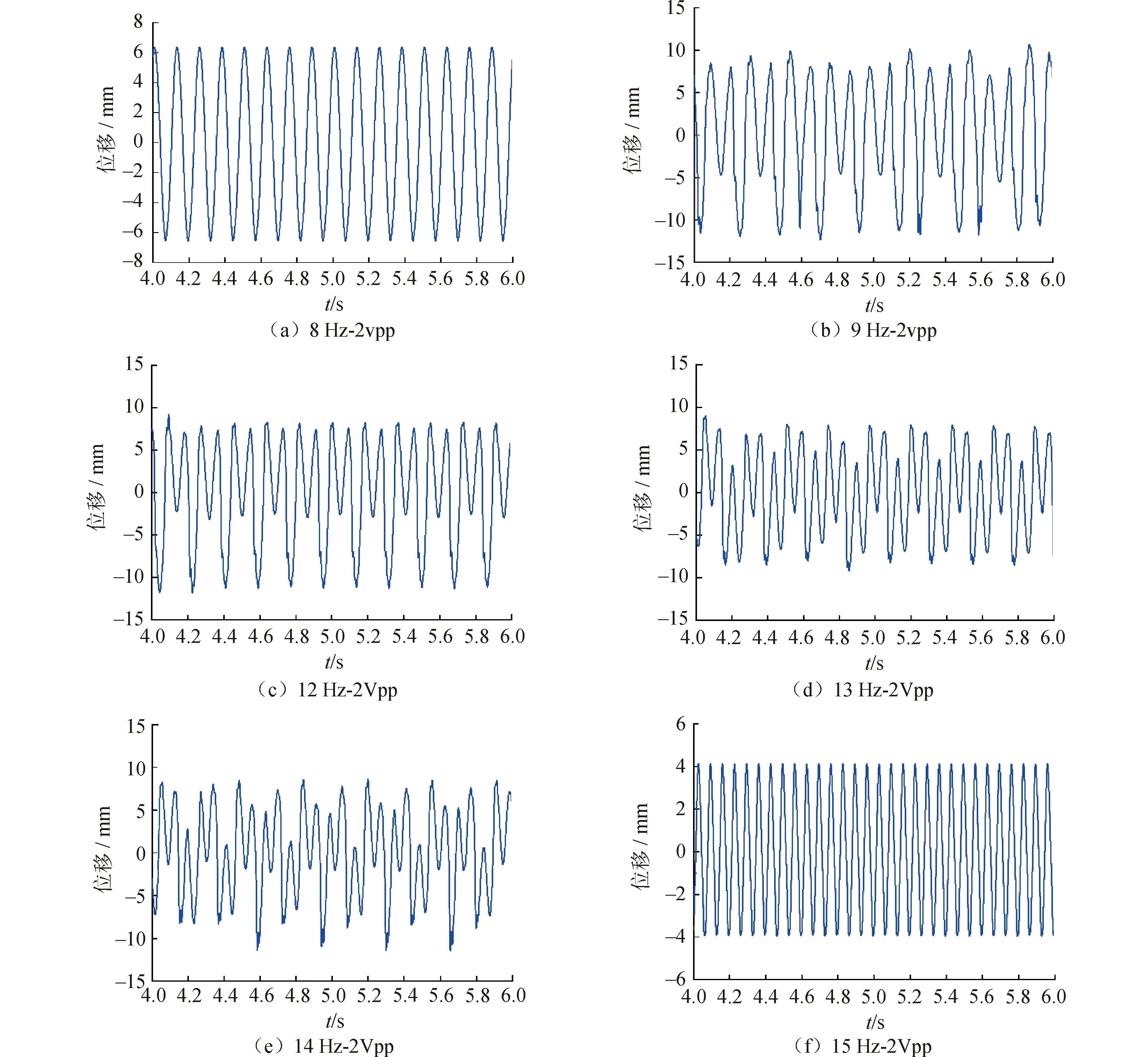
图8 不同频率下双稳态屈曲梁最高点的时间位移曲线Fig.8 Time-displacement curves of the highest point of a bistable buckling beam at different frequencies
4 结论
1)理论分析了新型双稳态屈曲梁结构的跳跃突变特性,并通过仿真分析验证了可行性,为新型双稳态屈曲梁结构的设计提供了理论依据;
2)实验分析发现新型双稳态屈曲梁结构在低频外部激励下发生了快速跳转,为低频减振和俘能结构的设计提供了新的思路。
