流固混合声子晶体中负折射与导波特性研究

杨帅， 李昌清， 赖虹君， 王艳锋

(1.安阳师范学院 建筑工程学院，河南 安阳 455000； 2.天津大学 机械工程学院， 天津 300350)

声子晶体是一种周期性排列的多相结构。由于其特有的物理特性，近些年受到了广泛的关注和研究[1-5],其中最引人注目的是能够操控弹性波的能力。通过单元结构的设计，可以较为自由地实现波的局域化、负折射、定向传播等奇异的物理特性。这些特性在吸声降噪[6-7]、振动控制[8-9]、声隐身斗篷[10-11]、声整流器件[12-13]等诸多领域具有广阔的应用前景。声子晶体在新效应、新特性等方面的研究极大地提高人们对声波的控制能力，有望实现功能器件性能的极大提升，为民用、军用高端装备及工业设备的设计带来巨大变革。本文研究了由工字型钢柱正方排列在空气中组成的声子晶体的波动特性，讨论了波在完好声子晶体中产生的负折射效应，并通过引入缺陷，分析了线性波导和耦合共振波导中导波的传播特性。

1 几何模型和计算方法

本文考虑工字型钢正方排列在空气中，如图1所示。其中单胞几何参数为：晶格常数a0=2 cm，工字型钢由3个相同的矩形组合而成，L=1.4 cm，t=0.2 cm。钢的密度ρs=7 800 kg/m3，弹性模量E=210 GPa，泊松比ν=0.275。空气的密度ρa=1.25 kg/m3，波速c=343 m/s。

机械波在固体中的传播形式为矢量波(可以分为纵波和横波)，而在流体中的传播形式为标量波(只有纵波)。因此，在计算流固耦合型声子晶体的能带结构时，不仅要将整个区域分为流体和固体区域，而且要在流固连接处建立合理的边界条件以满足实际情况。在流固界面法向位移和力连续，即：

Us·n=Uf·n

(1)

p·n=σ·n

(2)

式中：Us、Uf分别为固体和流体中的位移；n为流固界面的法向向量；p为界面处流体压强；σ为界面处固体的应力张量。因为流固体系具有相同周期的函数，根据Bloch定理，边界上应满足：

Us(r+a)=ei(k·a)Us(r)

(3)

p(r+a)=ei(k·a)p(r)

(4)

对于二维声子晶体，r=(x，y)为位置矢量；k=(kx，ky)为波矢且被限制在第一布里渊区内(图1所示)。

目前，计算声子晶体的方法有很多，比如传递矩阵法，平面波展开法，时域有限差分法，多重散射法和有限元法等[14]。其中有限元法在适用性、计算速度、精确度及收敛性等方面有着明显的优越性而被广泛应用。本文采用有限元软件Comsol Multiphysics进行计算。单胞内特征方程的离散形式为：

(K-ω2M)U=0

(5)

式中：U是节点位移；K和M分别是刚度矩阵和质量矩阵。需要说明的是，由于工字型散射体是长方形对称，故第一布里渊区与正方晶格的结果有些区别，如图1(c)所示。将波矢k遍历图1(c)所示的第一布里渊区进行计算，就可得到能带结构。

2 数值仿真结果

2.1 能带结构和响应谱

首先计算了图1所示声子晶体的能带结构，如图2(a)所示。同时，图中还给出了ΓX方向和ΓY方向含8个单胞有限结构的响应谱。分别在有限结构的一侧边界处施加一个长度为l的线源激励，在结构另一边拾取响应。为了消除反射的影响，在接收端加入完美匹配层。结构的响应值为：

(6)

式中|pt|和|pi|分别为透射波和入射波的压强幅值。在感兴趣的频率范围内计算并拾取响应，即可得到结构的频率响应函数。可以看出，图示频率范围内出现了5条完全带隙，带隙范围分别是5 500～6 000 Hz、9 335～10 092 Hz、10 186～11 055 Hz、17 210～17 690 Hz和20 200～20 700 Hz。图中阴影表示了主要的方向带隙。可以看到结构的响应在带隙内衰减明显，衰减域与方向带隙宽度几乎相同。ΓY方向能带结构在10 kHz和20 kHz附近出现2条平带。但10 kHz处的平带在响应谱中也能明显的看到，20 kHz处的平带却没有在响应谱中体现出来。为了探究原因，图中给出了这2条能带上Y点的振动模态。蓝色(深色)表示负压强，红色(浅色)表示正压强。可以看出，10 kHz附近平带对应的模态关于ΓY方向是对称的，因此可以被平面波源激发。而20 kHz附近平带对应的模态关于ΓY是反对称的，不能被平面波源激发。

另外，计算了工字型钢绕单胞中心逆时针旋转φ=45°单胞的能带结构，如图2(b)所示。图中阴影表示了主要的完全带隙。可以明显看出，此时的带隙明显变宽，相应主要的几条带隙范围分别变为：4 046～7 126 Hz、7 845～12 674 Hz、14 535～17 071 Hz、19 454～22 692 Hz和23 808～24 763 Hz。可见，旋转工字型钢会对结构的带隙产生明显的影响。与φ=0°时的情况类似，在20 kHz附近也出现了一条平带。图中给出了这条能带上Y点的振动模态。振动模态为中心对称模式，此种振动也不会被平面波源激发。

2.2 等频率曲线和负折射

等频率曲线反映的是波矢和频率之间的关系。计算等频率曲线的方法与计算能带结构类似，不同的是需要对整个布里渊区的波矢k进行遍历求解。本文图中用等效波数Ωx=kx·a0/π,Ωy=ky·a0/π表示横纵坐标，不同颜色表示相应的频率。声子晶体的强频散特性会使其等频率曲线非常复杂，进而出现群速度方向与波矢方向不一致的情况。这会在声子晶体中产生一些异常波动行为，如负折射。

图3为图1中单胞(φ=0°)第1阶能带的等频率曲线。从图中可以看出，在频率较小时，等频率曲线的形状为椭圆，但是随着频率的增大，等频率曲线的曲率在逐渐变小。在5.25 kHz时等频率曲线几乎为一条直线。

为了更加清晰地说明等频率曲线的意义，计算了不同频率下中心点源激励在周期结构中的传播，如图4所示。可以看出，在低频下，波可以向四周传播，且y方向波长大于x方向波长，声压场分布为一个个以y轴为长轴的同心椭圆(图4(a)、(b))。对比图3等频率曲线，由于波长和波矢的反比关系，在等频率曲线中为一个个以x轴为长轴的同心椭圆。而随着频率增大，波渐渐在x方向不能传播，对应等频率曲线中，随频率增大，等频率曲线由椭圆变成曲线(图4(c)、(d))。随着频率继续增大，等频率曲线渐渐变成直线，此时波只能沿y方向传播，图4(e)、(f)也验证了这一点。

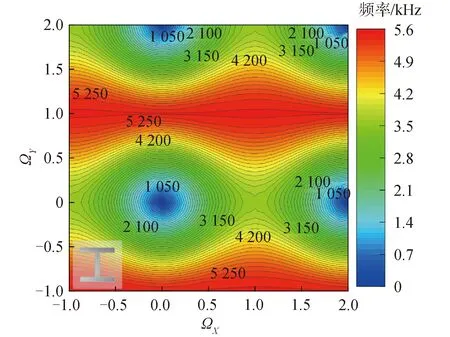
图3 φ=0°时一阶能带的等频率曲线Fig.3 Equifrequency contour of 1st band forφ=0°

图4 不同频率中心点源激励时的压强分布Fig.4 Pressure distribution of wave propagation under central point source at different frequencies

图3中等频率曲线在5.25 kHz时几乎为一条直线。这意味着在这个频率处，波的传播会表现出一定的方向性，仅沿y方向传播，如图4(f)所示。图5给出了5 255 Hz时波从45°方向入射到声子晶体后的声压场分布。由图5可知，波在声子晶体中以几乎垂直于法线的方向传播，并以相同的角度射出。这个现象与等频率曲线所显示的结果一致。

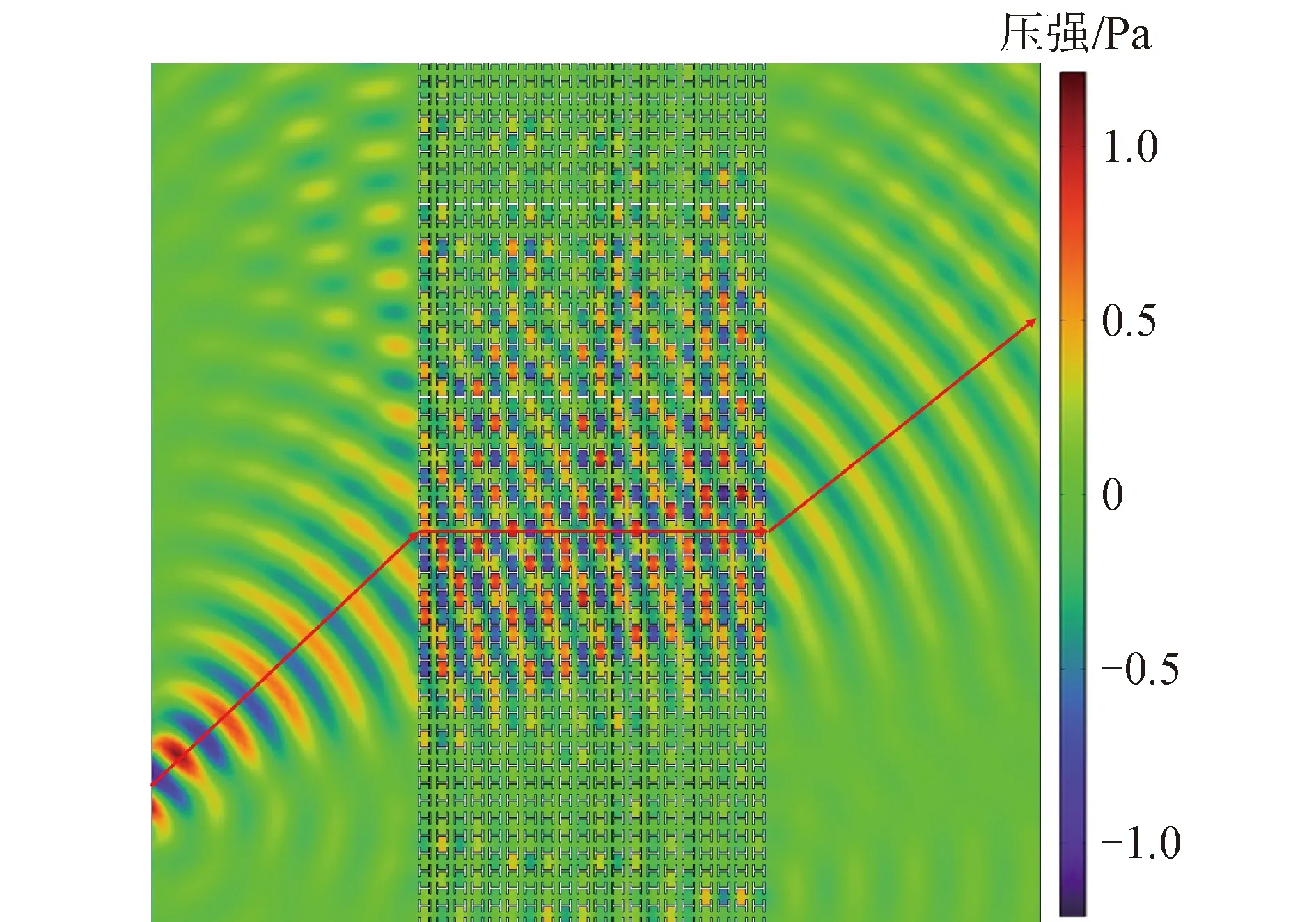
图5 φ=0°时波以5 255 Hz传播时的压强分布Fig.5 Pressure distribution of wave propagation at 5 255 Hz forφ=0°

另外，计算了φ=45°时单胞的第1阶能带的等频率曲线，如图6(a)所示。可以看出，随着频率的增大，等频率曲线先从正圆变成矩形，然后逐渐变回正圆。在一定的频率范围内，沿ΓM方向等频率曲线为直线且垂直于ΓM连线，这为负折射现象的产生提供了基础。图6(b)给出了3 045 Hz时波从45°方向入射(也就是沿ΓM方向)进入声子晶体后的声压场分布。从图中可以看出，声子晶体中的折射波与入射波在法线的同侧，也就是出现了负折射现象。随后，在出射界面，波以相同的角度射出。

2.3 缺陷态和波导

通过改变一排单胞的几何形状或材料，可以将理想的声子晶体转化为含线缺陷的声子晶体。线缺陷声子晶体容易使波在缺陷中传播，产生波导现象。因此线缺陷在声学滤波器和声学传感器领域具有很大的应用价值。为了研究工字型钢/空气二维声子晶体的波导特性，分别计算了具有中心缺陷的1×13超胞结构在ΓX方向上的能带结构和具有中心缺陷的1×13超胞结构在ΓY方向上的能带结构，即图7所示。图中阴影表示完美超胞的带隙。从图7可以看出，线缺陷的引入在ΓX方向带隙内出现了一条导波带，但在ΓY方向带隙内出现了2条导波带。从导波带的模态可以看出，P2点所在导波带受通带影响较大，局域性较差。其他2点则表现出良好的局域性。

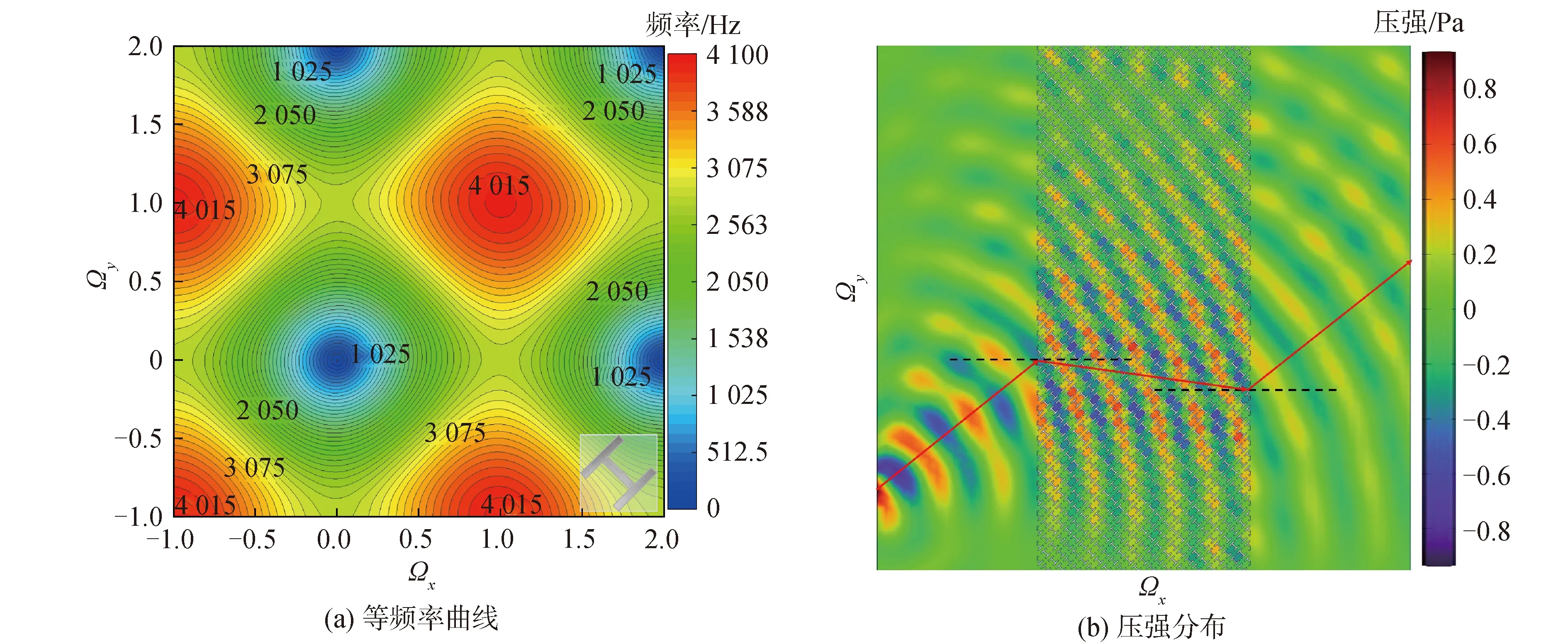
图6 φ=45°时一阶能带的等频率曲线和波以3 045 Hz传播时的压强分布Fig.6 Equifrequency contour of 1st band and pressure distribution of wave propagation at 3 045 Hz forφ=45°

图7 线性波导的能带结构和对应点的振动模态Fig.7 Band structures and vibration modes of linear waveguides

为了进一步研究导波的传播特性，采用有限元法计算了3种由13×13单胞组成的有限阵列结构的响应，如图8所示。设计了3种线缺陷形式，分别为沿x方向直线型，沿y方向直线型和Z型。其响应分别用虚线、短点线和实线在图中标识。相应阴影区域表示不同缺陷可以形成波导的范围。从图中可以看出，x方向直线型缺陷结构在5.5～8.5 kHz出现峰值，意味着波在这个频率内可以很好地通过。对于y方向直线型缺陷结构，其响应在5～6.8 kHz出现峰值。对比图7可以发现，响应谱的峰值范围与相应方向超胞的带隙范围基本重合。也说明了不同方向的波导一般会出现在不同带隙范围内。对于Z型线性波导，响应谱的峰值出现在大约5.8～6.7 kHz。可以看出，这个范围在前2种缺陷结构响应谱峰值范围的交集内，这是由于Z型线性波导本质上是由x方向直线型和y方向直线型2种线性波导组合而成。

为了更清晰地显示导波现象，图9给出了波在2种直线型波导中传播的声压场分布。从图9(a)中可以看出，波在x方向直线型线性波导中可以很好地传播，其传播模态与图7(a)所示模态一致。相似的情况也发生在y方向直线型线性波导中，如图9(b)所示。但只有图7(b)P1点所对应的模态被激发。

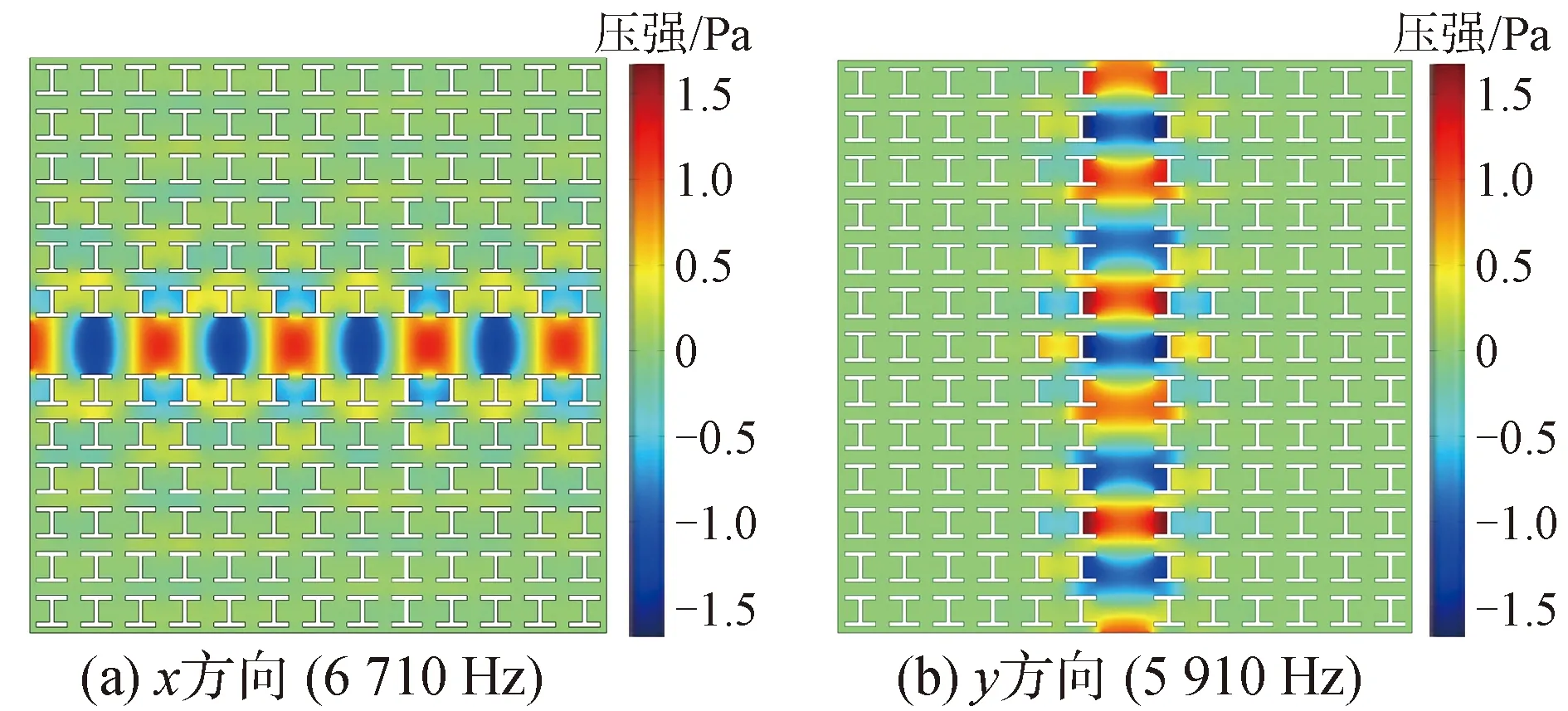
图9 直线型波导传播时的压强分布Fig.9 Pressure distributions of linear waveguides

接下来计算了波在Z型线性波导中的传播，压力分布如图10所示。由图可知，频率为6 520 Hz时波在Z型线性波导中能够较好地传播，而在7 470 Hz时，波并不能沿缺陷传播。这是由于Z型线性波导包含x方向和y方向2种直线型线性波导，其导波产生的频率范围必须在2种直线型线性波导共同的导波频率范围内。

由一系列缺陷腔或共振体周期排列形成的耦合共振波导，可以实现很强的局域性和低群速度传输[15]。为了研究耦合共振波导的波动特性，首先分别计算了耦合共振波导在ΓX方向(2×13单胞)和ΓY方向(2×13单胞)的能带结构，如图11所示。图中阴影表示完美超胞的带隙。从图11可以看出，耦合缺陷的引入在ΓX方向和ΓY方向带隙内均出现了一条导波带，范围分别为6.1～6.5 kHz和5.5～5.8 kHz。从模态图可以看出，导波均呈现一定的局域性，且ΓX方向局域性相对较强。

图10 Z型线性波导中波传播时的压强分布Fig.10 Pressure distribution of Z-type linear waveguide

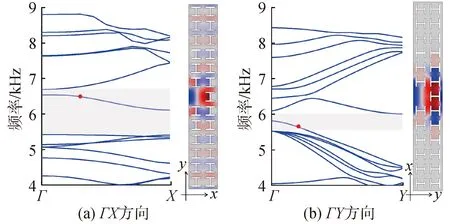
图11 耦合共振波导的能带结构和对应点的振动模态Fig.11 Band structures and vibration modes of coupled-resonator waveguides

接下来，研究了耦合共振波导的传播特性。同样采用有限元法计算了2种由13×13单胞组成的有限波导结构的响应，如图12所示。设计了沿x方向和y方向的2种直线型耦合共振波导。其响应分别用点划线和实线在图中标识。相应阴影区域表示不同缺陷可以形成耦合共振波导的范围。

图12 直线型耦合共振波导的响应谱和计算模型Fig.12 Transmission spectrum of straight coupled-resonantor waveguides and calculation models

从图中可以看出，x方向直线型耦合共振波导在6.1～6.5 kHz和8.7～8.9 kHz范围出现峰值，意味着波在这个频率内可以很好的通过。对于y方向直线型耦合共振波导，其响应在5.1～5.8 kHz出现峰值。2个响应谱的峰值范围没有重合，这与图11能带结果相一致。同时这也意味着波不能在弯折耦合共振波导中传播。

为了更清晰地显示波导现象，图13给出了波在2种直线型耦合共振波导中传播的声压场分布。从图13(a)中可以看出，波在x方向直线型耦合共振波导中可以很好地传播，但是相比图9(a)，能量有些发散。相似的情况也发生在y方向直线型耦合共振波导中，如图13(b)所示。

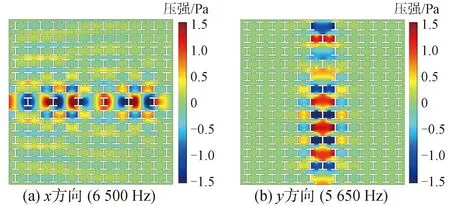
图13 直线型耦合共振波导中波传播时的压强分布Fig.13 Pressure distributions of straight coupled-resonantor waveguides

3 结论

1)计算了2种结构的等频率曲线，阐明不同形状等频率曲线的意义，并进一步研究了声子晶体中出现的负折射现象。

2)研究了含线缺陷以及耦合共振缺陷结构中导波的传播特性，说明结构中产生波导的条件，计算了直线型和Z型线性波导以及直线型耦合共振波导的波动特性，说明了复杂(如Z型)波导中导波存在的条件。