一种预变形周期刚架结构振动带隙特性分析

郭振坤， 温佳琦， 张军， 董挺

(1.北京建筑大学 机电与车辆工程学院， 北京 102616； 2.北京理工大学 机械与车辆学院， 北京 100081)

工程减振问题在现代工程研究中十分常见[1]，为满足工业和运输业高速发展的需求，各种机械装置、精密仪器受到振动的影响愈加突出[2]，同时为加快国防现代化的脚步，要求飞机、坦克、舰船等能够在最为恶劣的环境中工作[3]，其工作性能都与减振技术密切相关。因此，关于如何减振的研究一直在持续，最行之有效的方法是究其原因对症下药，学者们做出了很多有价值的研究[4-5]。

周期结构因为其独特的减振优势，在许多工程领域越来越受到关注，例如声子晶体和光子晶体。Kushwaha等[6]利用平面波展开法研究了声子晶体带隙，即可以在某些频率范围内，阻止弹性波或声波的传播。这些阻止波传播的频率范围称为频率禁带，而那些允许波传播的频率范围称为频率通带；当振动或波的频率处于周期结构的频率带隙内时，将无法被传递。这样的禁带特性吸引了国内外众多学者进行研究，温激鸿等[7]利用周期弹簧振子结构简化了声子晶体，研究了声子晶体的振动特性，此后众多学者在此基础上研究了多种结构的振动带隙并将其应用于振动抑制和减振降噪等工程领域。

对于周期性声子晶体结构，通常可以通过改变部件的拓扑结构、刚度、密度或在某些局部增加共振器来优化振动和弹性波的传播特性。Yu等[8]利用传递矩阵法(TMM)研究了局域共振超材料梁的弯曲波衰减特性，其中局域振子是由软橡胶环和铜环设计而成。在此基础上，为提高工程适用能力和减振效果，针对如何根据实际工程环境灵活调整带隙位置和宽度，学者们完成了大量的设计和研究工作[9-11]。

周期刚架结构作为在工程建筑、机械中常见的结构也受到了广泛的关注。吴志静等[12]采用谱元法研究了周期桁架结构的振动带隙特性，这种方法具有在中高频区域计算误差小、划分单元少且计算效率高等优点。基于该方法，Zuo等[13]通过进一步改变结构构型和几何参数等对周期刚架结构进行设计优化，并讨论了影响带隙特性的因素。一些学者还提出了较为新颖的超材料结构。蔡昌琦等[14]利用准零刚度理论设计出一种具有低频带隙区间嵌入式准零刚度振子的新型超材料梁。Muhammad等[15]提出了一种具有超宽带隙的周期性和非周期性3D复合超结构，采用聚合物外壳的设计和球形/圆柱形钢块的嵌入，提高共振的动态特性和机械性能，使其拥有非常明显的低频带隙。进一步，一些研究者发现还可以通过结构元件的特定预变形来控制周期结构的振动和波传播特性。Mellmann等[16]提出一种预变形网格结构，计算了波在这种网格结构中的传播特性，发现可以通过结构预变形灵活地调控波带隙的位置和宽度。受此启发，本文设计了一种预变形周期刚架结构，通过内部构件的预变形实现刚度的调节，进而控制波带隙特性。此外，利用有限元方法进行了模态分析和振动透射率的计算，验证谱元法的正确性。

1 动力学模型

图1(a)所示为左端固支的预变形周期刚架结构，该结构包含20个单胞，每个单胞由11根梁/杆结构组成，由图1(b)看出，该单胞结构是通过将X型结构进行折断所形成，变形角用α表示。

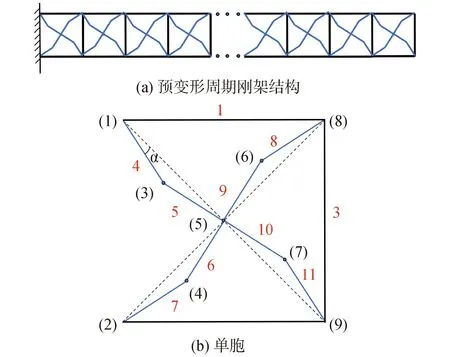
图1 预变形周期刚架结构示意Fig.1 Schematic diagram of the pre-deformed periodic rigid frame structure

1.1 杆单元求解

轴向振动杆件的偏微分运动方程表示为：

(1)

式中：u(x,t)为轴向位移；E和ρ分别是材料弹性模量和密度；A是杆件横截面积。式(1)的解可以假设成：

(2)

式中：Un(x,ωn)为微元的轴向位移；ωn为杆的圆频率。

将式(2)代入(1)中可以得到对于每个离散的频率ωn的特征值问题：

EAU″+ω2ρAU=0

(3)

假设其通解为：

U(x)=be-ik(ω)x

(4)

将式(4)代入式(3)中得到色散关系：

(5)

即可得到2个实根k1和k2：

k1=-k2=kL

(6)

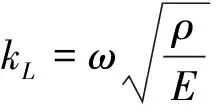
将式(6)代回式(4)可得：

U(x)=b1e-ikLx+b2eikLx

(7)

则对于长度为L的杆可以用矩阵形式来表示：

U(x)=e(x,ω)b

(8)

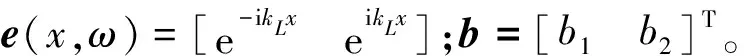
用U1和U2表示杆件两端的节点位移，则有U1=U(0)和U2=U(L)，可以记为：

(9)

(10)

令dR=HR(ω)b,则有：

(11)

用N1和N2表示杆件两端节点力，杆的节点力函数为N(x)。

整理可得:

(12)

式中：NR1(x,ω)=csc(kLL)sin(kL(L-x));NR2(x,ω)=csc(kLL)sin(kLx)。

(13)

轴向力分量与U(x)有关，即：

N(x)=EAU′(x)

(14)

将节点位移代入式(4)，可得：

U(x)=NR1U1+NR2U2

(15)

类似地，轴向力也可以写成谱表达式，表示为：

(16)

节点轴向力和由材料强度定义的内部力之间的平衡条件有：

(17)

则有：

SR(ω)dR=fc(ω)

(18)

根据轴向力与位移的关系，可以得到频域上位移与节点力的关系：

(19)

式中SR(ω)为杆单元的刚度矩阵，可以表示为：

(20)

(21)

整理可得:

(22)

1.2 梁单元求解

类似地，可以推导出梁单元位移与节点力的关系。Timoshenko梁的横向振动需要考虑转动惯量和剪切变形，用谱表达式对横向位移w(x,t)和转角θ(x,t)分别进行表示：

(23)

(24)

梁的横向振动偏微分方程为：

(25)

(26)

式中：κ的取值与截面形状有关；G是剪切模量；A是横截面积；I是截面惯性矩。

将式(23)和(24)代入偏微分方程(25)、(26)中得:

(27)

(28)

式(27)、(28)的通解分别假设为：W(x)=ae-ik(ω)x和Θ(x)=βeik(ω)x，可得:

(29)

则有：

(30)

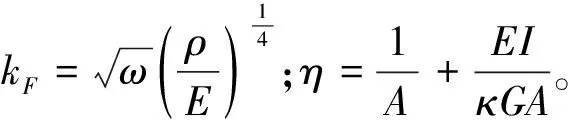
求解方程(30)可以得到4个根：

k1=-k2=

(31)

k2=-k4=

(32)

代入式(29)中可得:

(33)

(34)

由此，式(27)和(28)的通解可得:

W(x,ω)=a1e-iktx+a2eiktx+a3e-ikex+a4eikex=

ew(x,ω)a

(35)

Θ(x,ω)=β1a1e-iktx+β2a2eiktx+β3a3e-ikex+

β4a4eikex=eθ(x,ω)a

(36)

其中：

(37)

(38)

eθ(x,ω)=ew(x,ω)B(ω)

(39)

梁的两端节点位移和转角可以表示为：

(40)

将式(35)和(36)代入式(40)可得:

(41)

式中：

(42)

(43)

将式(41)代入到式(35)和(36)中可得:

(44)

(45)

梁的节点力为：

(46)

将节点力表示为谱表达形式：

(47)

(48)

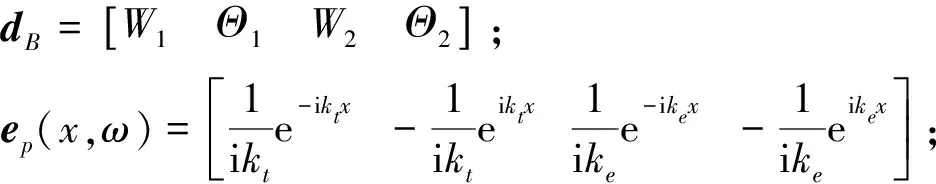
es(x,ω)=[-ktrte-iktx-ktrteiktx-keree-ikex-kereeikex]。

则有端点位移与力的关系为：

(49)

即：

SB(ω)dB=f

(50)

式中SB(ω)为Timoshenko梁的单元刚度矩阵：

(51)

其中：

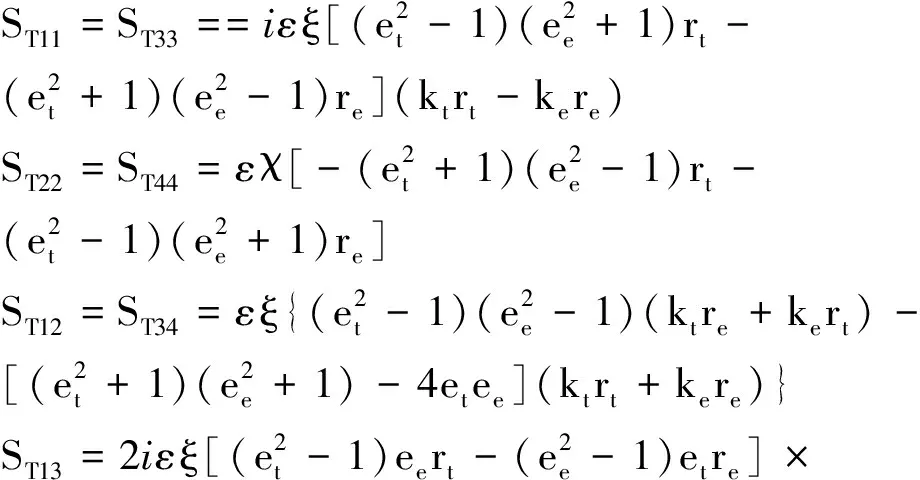
最终推导出总的力与位移的关系为：

FB=SB(ω)UB

(52)

式中：FB和UB为节点力矩阵和节点位移矩阵；SB(ω)为刚度矩阵。

1.3 整体结构组装

利用坐标转换矩阵，将上述梁、杆结构的节点力和节点位移从局部坐标系转换为整体坐标系，并采用有限元组装和矩阵组合的方法，可得到每一个子结构在整体坐标系下的动力学刚度矩阵：

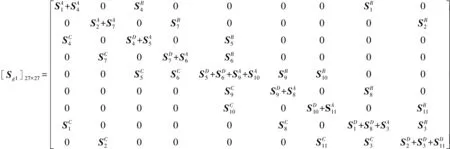
(53)

(54)

式中n=1,2,3,4,5,6,7,8,9,10,11。进而可以得到图1(a)所示周期刚架结构的节点位移与节点力的关系：

F=S(ω)U

(55)

式中：S(ω)为3(7m+2)×3(7m+2)的动力学刚度矩阵；m是单胞周期数。对式(55)进行求解，即可完成结构动力学计算。

2 数值模拟

为分析预变形周期刚架结构振动带隙特性，取20个单胞组成整体结构，一端施加固定约束，每个单胞均由实心圆截面杆组成，其中横杆和竖杆长度分别用l1和l2来表示，且l1=l2=1 m，圆截面半径r=0.04 m，变形角α=π/12。材料参数为：ρ=7 800 kg/m3，E=210 GPa。通过求解式(10)特征值问题，可以得到结构的固有频率。

为验证SEM建模和编程求解的正确性，采用有限元商业软件ANSYS进行仿真计算。此外，还计算了无预变形的X型周期刚架结构(如图1(b)虚线所示，即α=0)固有频率。为保证合理性，基于质量守恒定律，在确定2种结构单胞跨度相等的前提下，调整X型结构杆件的圆截面半径，令其等于0.040 7 m。

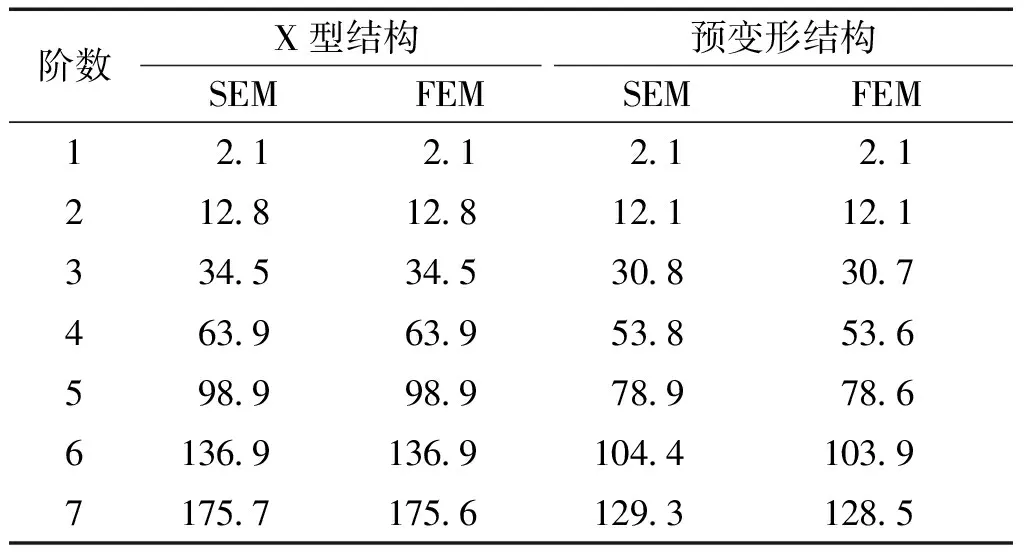
表1 2种不同刚架结构固有频率

图2 预变形周期刚架结构前四阶振型Fig.2 The first fourth vibration modes of the pre-deformed periodic rigid frame structure

图4表示的是周期刚架结构的频域分析，在固定端施加竖直向下、大小为1 N的简谐力，通过求解式(55)，取自由端点响应与固定端位置响应的比值，可以得到振动透射率。可以发现该结构的频响曲线具有多处低谷，即振动带隙，FEM结果较好地验证了SEM计算得到的振动带隙结果的正确性。

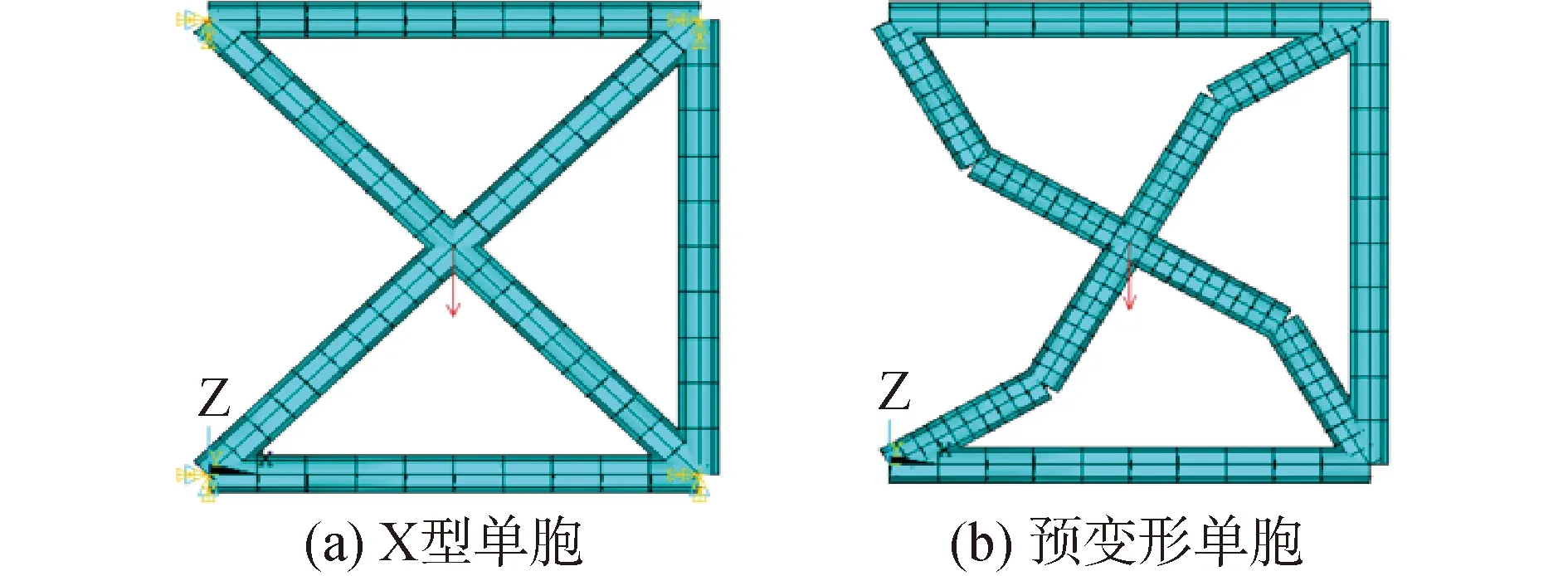
图3 2种不同单胞结构Fig.3 Two different unit cells

图4 2种不同周期刚架结构的频响透射率曲线Fig.4 Frequency response transmittance of two different rigid frame structures

此外，通过比较可知，预变形刚架结构第1个振动带隙位置比X型刚架结构出现在更低频的位置，前者的频率范围大致是210～258 Hz，而后者的频率范围是270～338 Hz。并且预变形刚架结构在1 576～1 753 Hz频率范围内有一个更宽的振动带隙。因此，可以得出结论，预变形周期结构可以实现更加低频的振动带隙。

图4中通过透射率，即自由端点位置响应与固定端位置响应的比值来判断结构的振动带隙范围，当自由端点的位置响应较小时，频响曲线出现低谷，且响应越小对应的透射率也就越小，这就会出现结构恰好不处于带隙区间范围内而选择的自由端点因受迫振动产生的响应很小的情况，这种情况可以通过观察带隙区间外和区间内对应的模态进行比较来辨别。比如从图4中发现预变形结构的第1个振动带隙区间为210～258 Hz，所以选取了120 Hz和222 Hz 2个频率，如图5(a)、(b)分别为对应频率的模态，可以看出120 Hz频率下自由端点的位置响应较大，且这种模态不属于带隙区间内，因为没有抑制振动波在结构内传播；相对而言222 Hz频率下自由端点的位置响应很小，几乎没有，对应的模态表明振动受到了抑制，后面几个周期的单胞几乎没有受到影响，符合了结构的带隙特性，可以进一步证明带隙的存在以及结果正确性。

图5 预变形周期刚架结构的振动模态Fig.5 Vibration modes of the pre-deformed rigid frame structures

3 结论

1)分析确定了结构的振动带隙，预变形结构的刚度比X型结构的刚度更低，证明了预变形结构可以实现更低频的振动带隙的同时，在高频区域产生更宽频的带隙；

2)在仿真计算中取自由端点响应与固定端位置响应的比值，得到振动透射率，通过FEM验证了上述理论结果，并定性分析了预变形结构固有频率更低的原因；

3)通过自由端点位置响应与固定端位置响应的比值来判断结构的振动带隙范围，会出现结构恰好不处于带隙区间范围内而选择的自由端点因受迫振动产生的响应很小的情况，这种情况可以通过观察模态进行辨别，禁带范围内振动波在经过几个周期内就会得到充分抑制，可以进一步证明带隙的存在以及结果正确性；

4)在此基础上，可以在工程结构设计过程中考虑调节变形角α的大小，来改变结构的刚度，以获得更符合条件的振动带隙特性，但要兼顾结构稳定性的问题。