含双质量谐振单元的声学超材料杆的纵波传播
2022-10-09武恒星娄佳
武恒星, 娄佳
(宁波大学 工程力学系,浙江 宁波 315211)
声子晶体具有某种形式的空间周期性,可以是组分材料、内部几何或边界条件[1-4]。与光子晶体类似,基于Bragg散射机制,声子晶体可以阻止特定频率范围内的声波/弹性波传播[5- 6],将这样的频率范围称为Bragg禁带。Mead等[7]研究了具有周期性边界条件的无限梁的波传播问题,揭示了该结构的频带特征。Ruzzene等[8-9]将周期性结构的概念应用于夹芯板,研究表明,通过使不同的芯体材料周期排列,可以阻止特定频率范围内的弹性波在某一方向的传播。Bragg禁带的产生要求晶格尺寸与弹性波的波长相当。那么,长波长就意味着不切实际的巨大结构。这使得声子晶体不适用于低频波操纵或振动抑制[10-11]。Liu等[12]实现了声学/弹性超材料。他们通过将局域共振单元引入周期性结构获得了亚波长禁带。与声子晶体相比,声学/弹性超材料的显著优势在于其可以更加紧凑、轻质,尤其适用于低频波操纵。
受到Liu的启发,科研人员对声学/弹性超材料进行了广泛的研究,包括质量-弹簧系统[13-14]、梁[15-17]、板[18-19]等。具体来说,Huang等[20]研究了一个复合链式系统,指出在局域共振频率附近系统表现出负有效质量。Airoldi等[21]设计了一种周期性粘贴分流压电片的可调节超材料梁,揭示了其禁带特征。Assouar等[22]研究了一种由薄铝板和其上周期性排列的柱体构成的声学超材料板,并通过实验证实了其可以在亚波长范围内实现波导以及波的捕获。大量的研究表明,声学/弹性超材料在很多领域具有潜在应用,如声学透镜[23]、声学/弹性斗篷[24]、亚波长成像[25]等。
众所周知,各向同性均匀材料中传播的纵波是无色散的(群速度等于相速度)。而在均匀介质中引入周期性夹杂(与母材具有不同弹性参数的介质)将显著影响弹性波的传播。在此方面,Wang等[26]研究了纵波(和面内横波)在一维声子晶体中的传播问题。该声子晶体由2种(或3种)组元周期排列构成。Xiao等[27]设计了一种由均匀介质和多质量谐振单元构成的声学超材料杆,并计算了其频带结构,研究结果表明多质量谐振单元可用于获得多个亚波长禁带。Khajehtourian等[28]研究了由均匀介质和周期性谐振器构成的声学超材料杆中纵波的传播。与以往的工作不同,他们考虑了基体材料的几何非线性。
本文设计了一种新型声学超材料,其基体是由2种组元构成的杆,每个胞元内部附加一个双质量谐振单元。采用Bloch定理给出了该结构色散关系的解析解。该解析模型可退化用于求解声子晶体杆和含有单质量谐振单元的声学超材料杆的色散。探索了利用Bragg散射机制和局域共振机制的耦合作用获得宽频禁带和/或多个禁带的途径。
1 模型建立
声学超材料杆如图1所示。其基体材料由2种组元周期排列构成,每个胞元内部附加一个双质量谐振单元。本文将研究该声学超材料杆中纵波的传播。

图1 声学超材料杆示意Fig.1 Sketch of the acoustic metamaterial rod
杆的纵向运动控制方程为:
(1)
式中:Ej表示杨氏模量;ρj表示质量密度;u1表示杆的纵向位移;t表示时间;j=A或B表示不同的组分材料。
控制方程(1)的解写为:
(2)
(3)
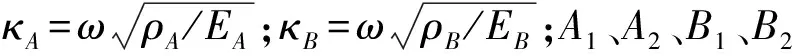
A2exp(-iκAx)]exp(-iωt)
(4)
B2exp(-iκBx)]exp(-iωt)
(5)
对于每个谐振单元,质量m1和m2的运动方程为:
(6)
(7)
式中:um1和um2分别表示质量m1和m2沿x方向的位移;位移分量上方的点表示对时间t求导。

(8)
将式(8)代入式(7),有:
(9)
将式(8)和式(9)代入式(6)可得:
Um1=
(10)
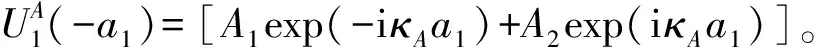
在材料A和材料B的界面处,位移和应力都应该是连续的,即:
(11)
将式(2)~(5)代入式(11)可得:
A1+A2=B1+B2
(12)
κAEA(A1-A2)=κBEB(B1-B2)
(13)
由式(12)和(13),B1和B2可以用A1和A2表示为:
(14)
(15)
每个胞元左右两端的位移和轴力应该满足Bloch定理,即:
(16)
(17)
式中:a1和a2分别表示每个胞元内2种组元的长度,a=a1+a2;κ表示波数;S表示杆的横截面积;F表示谐振单元给杆的力,以沿坐标轴的正方向为正。
(18)
将式(2),(8)1和式(10)代入式(18),有:

(19)
将式(19)代入式(17),并利用式(2)~(5),可得:
exp(iκBa2)B1+exp(-iκBa2)B2=
exp(iκa)[exp(-iκAa1)A1+exp(iκAa1)A2]
(20)
EB(iκB)[exp(iκBa2)B1-exp(-iκBa2)B2]=
exp(iκa){EA(iκA)[exp(-iκAa1)A1-
exp(iκAa1)A2]+Γ[exp(-iκAa1)A1+
exp(iκAa1)A2]}
(21)
其中:

(22)
式(21)还可以写作:
iκBEBexp(iκBa2)B1-iκBEBexp(-iκBa2)B2=
exp(iκa)[(iκAEA+Γ)exp(-iκAa1)A1+
(-iκAEA+Γ)exp(iκAa1)A2]
(23)
将式(14)、(15)代入式(20)、(23),有:
(24)
(25)
式中β=exp(iκa)。
由式(24)和(25)构成的方程组有非零解{A1,A2}的条件为其相应的系数行列式为零。据此,对于每一个ω,可以得到β的闭合解为:
(26)
其中:
L=b11b22-b12b21
M=a11b22+a22b11-a12b21-a21b12
N=a11a22-a12a21
a11=exp(iκBa2)[1+κAEA/(κBEB)]+
exp(-iκBa2)[1-κAEA/(κBEB)]
a12=exp(iκBa2)[1-κAEA/(κBEB)]+
exp(-iκBa2)[1+κAEA/(κBEB)]
a21=iκBEBexp(iκBa2)[1+κAEA/(κBEB)]-
iκBEBexp(-iκBa2)[1-κAEA/(κBEB)]
a22=iκBEBexp(iκBa2)[1-κAEA/(κBEB)]-
iκBEBexp(-iκBa2)[1+κAEA/(κBEB)]
b11=-2exp(-iκAa1)
b12=-2exp(iκAa1)
b21=-2(iκAEA+Γ)exp(-iκAa1)
b22=-2(-iκAEA+Γ)exp(iκAa1)
由此,可以得到波数的解析解为:
κ=(-i/a)lnβ
(27)
2 结果与讨论
本节将分别计算声子晶体杆、含单质量谐振单元的声学超材料杆以及含双质量谐振单元的声学超材料杆的频带结构并进行比较。
定义几何和材料参数如下:
1)每个胞元中,材料A和材料B的长度分别为a1=a2=0.2 m,杆的横截面积为S=0.01 m2;
2)材料A选用ABS聚合物,其材料参数为ρA=1 040 kg/m3,EA=2.4 GPa;材料B选用金属铝,其材料参数为ρB=2 700 kg/m3,EB=68.9 GPa。
同时,定义如下无量纲参数:


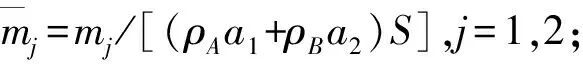
2.1 声子晶体杆的频带结构


图2 声子晶体杆的频带结构Fig.2 Band structure of the phononic crystal rod
2.2 含单质量谐振单元的声学超材料杆的频带结构
这一节中,计算含单质量谐振单元的声学超材料杆的频带结构。令m2=0,式(22)退化为:
(28)


图3 含单质量谐振单元的声学超材料杆的频带结构Fig.3 Band structure of the acoustic metamaterial rod with single-mass resonant units
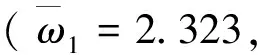

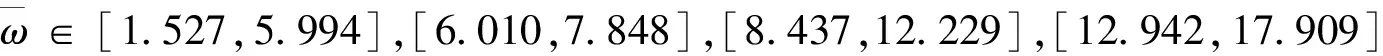
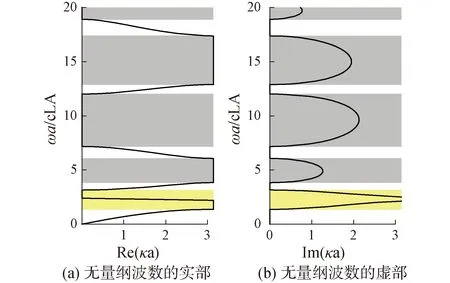
图4 含单质量谐振单元的声学超材料杆的频带结构Fig.4 Band structure of the acoustic metamaterial rod with single-mass resonant units

图5 含单质量谐振单元的声学超材料杆的频带结构Fig.5 Band structure of the acoustic metamaterial rod with single-mass resonant units
2.3 含双质量谐振单元的声学超材料杆的频带结构
下面将对含双质量谐振单元的声学超材料杆进行设计。对于双质量谐振单元,其在无阻尼情况下的固有频率可由下式计算:
m1m2ω4-[m2k1+(m1+m2)k2]ω2+k1k2=0
(29)

(30)
(31)

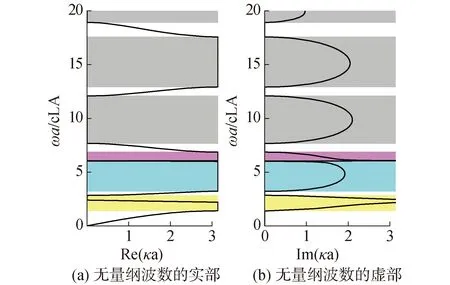
图6 k1=1.504×109 N/m,k2=3.830×108 N/m时无量纲波数的实部和虚部Fig.6 Band structure of the acoustic metamaterial rod with bi-mass resonant units

图7 k1=7.660×108 N/m,k2=7.520×108 N/m时无量纲波数的实部和虚部Fig.7 Band structure of the acoustic metamaterial rod with bi-mass resonant units
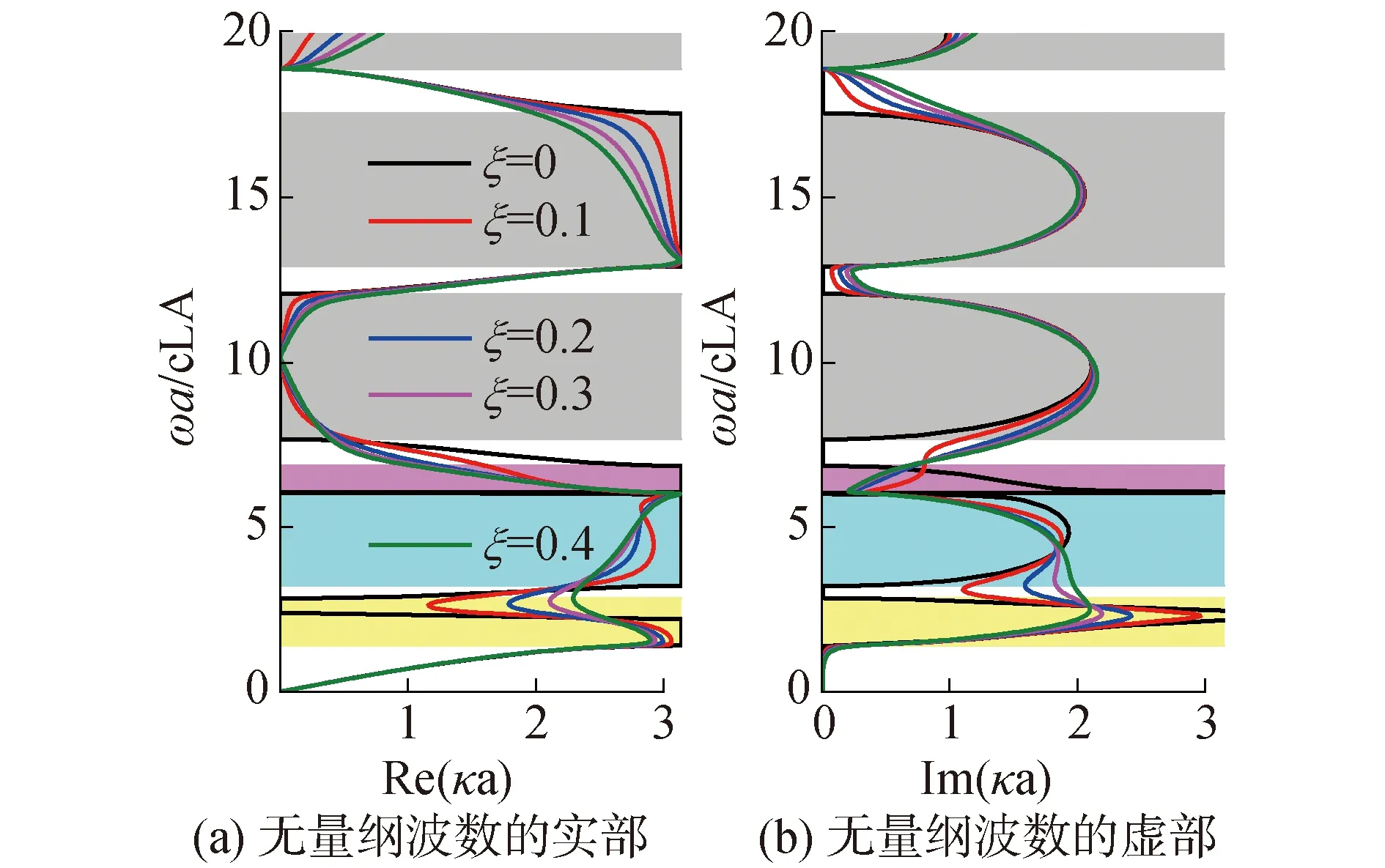
图8 k1=1.504×109 N/m,k2=3.830×108 N/m时无量纲波数的实部和虚部Fig.8 Band structure of the acoustic metamaterial rod with bi-mass resonant units
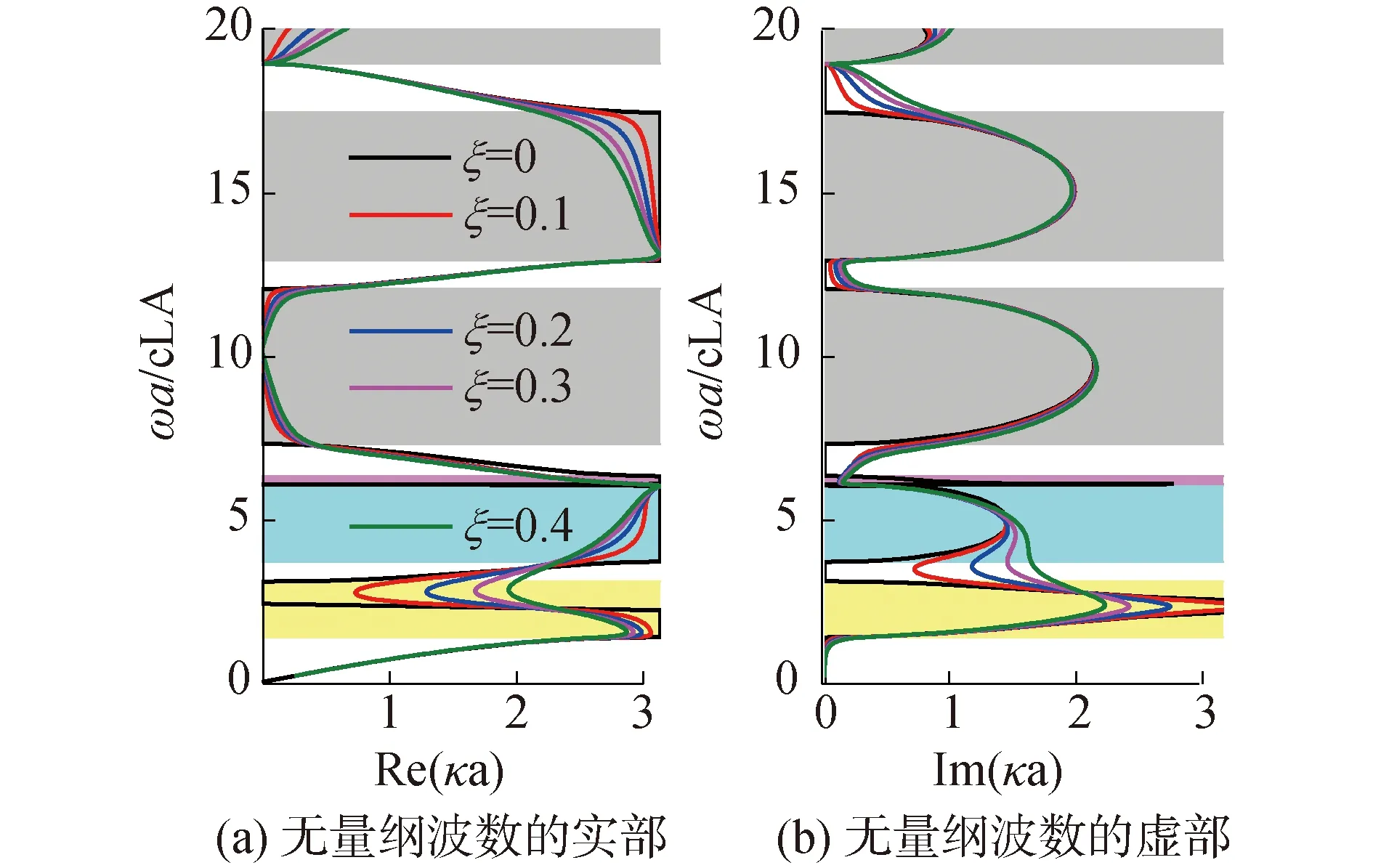
图9 k1=7.660×108 N/m,k2=7.520×108 N/m时无量纲波数的实部和虚部Fig.9 Band structure of the acoustic metamaterial rod with bi-mass resonant units
3 结论
1)可以利用Bragg散射机制和局域共振机制的耦合获得宽频禁带;
2)对于含单质量谐振单元的声学超材料杆,若谐振单元的固有频率与相应声子晶体杆的第一Bragg禁带的截止频率重合,可以产生较宽的禁带;
3)引入双质量谐振单元将增强声学超材料杆的可设计性,有利于获得低频且相对较宽的禁带;
4)在谐振单元中引入适当阻尼,则可以进一步拓宽禁带。
本研究将为声学超材料的设计和应用以及低频范围内的弹性波操纵和振动抑制提供理论指导。
