热超构材料的时间相关非互易传热性能
2022-10-09宿一书熊健
宿一书, 熊健
(哈尔滨工业大学 航天学院复合材料与结构研究所,黑龙江 哈尔滨 150001)
超材料的概念起源于前苏联科学家Veselago在1967年提出的“负折射材料”概念[1],后来Pendry[2]提出超材料的概念,并被应用到了热学领域[3]。在热学领域,学者们运用热超构材料实现了多种热功能,比如热隐身[4-5]、热集中[6]、热透明[7]、热伪装[8]以及宏观二极管[9]和温度捕获[10]等。热超构材料的发展也为非互易性热传递的研究提供了新的思路。Torrent等[11]将时空调制引入到热超构材料设计,不借助于非线性材料在宏观尺度上实现了非互易性热传递。至此,时空调制开始成为热超材料设计的一种重要手段,学者们借助于机械能的持续输入设计了时刻调制系统,产生了很多有意义的成果[12-16]。
总的来说,在热扩散研究背景下,打破稳态下热传导方程的对称性、实现非互易性热传递[17-18]通常有2种方法,1) 借助于非线性材料[19-21],即材料的热导率随温度是变化的;2) 借助于额外的机械能输入[11],通过机械操作使材料参数在时间与空间尺度上具有可调谐性[22]。但是这些研究仅考虑了稳态条件[23-24],忽略了系统达到稳态之前,也就是瞬态[25-26]下的系统所展示的对称或者非对称的传热特性。宏观尺度的热传递现象的达到稳态之前的时间作为“系统反应时间”是不可忽略的,因为这将直接影响对系统的稳态功能(如热整流)的应用。因而瞬态的非对称传热特性在热管理[27]及热计算[28]等领域同样具有重要的研究意义。
在此既不借助于非线性材料,也不考虑机械能的额外做功输入,在线性非均匀材料体系下探究瞬态热传导过程中的非互易性。由于不考虑外功的输入,因此寻求的是材料参数在空间尺度上的调控,而不是时间空间的同时调控。
1 时间相关非互易热构超材料的存在条件
与稳态热传导过程仅需考虑热导率参数不同,非稳态的热传导过程有2组参数可以考虑,分别为热导率κ和密度比热容的乘积ρc。在非均匀传热介质中,参数匹配准则表示热导率的分布函数与密度比热容乘积的分布函数不满足某种特定对称规律。当系统中热导率κ与密度比热容乘积ρc2种参数在空间尺度下分布规律不一致而满足参数失配准则时,系统有可能实现非互易性热传递。
假设热超构材料整体的热导率为常数,即κ=常数,而密度与比热容的乘积为非均匀分布ρc(r)。此时,瞬态热传导方程可以写为:
(1)

(2)
在热流方向互逆的2种情况中,边界条件分别为Tx=0=T1、Tx=l=T2和Tx=l=T2、Tx=0=T1(T1 (3) 其初始条件转变为: (4) 将非齐次边界条件转化为齐次边界条件后,方程(2)的解可以表示为齐次边界方程(3)的解与2个单一非齐次边界条件方程解的组合: (5) 下面对方程(3)进行求解,除了数值方法以外,求其解析解的方法主要有离散法[30]和分离变量法[30]。此处选用分离变量法,设u(x,t)=X(x)Γ(t),方程(3)可以分解为: (6) λ为特征值,根据边界条件和初始条件,可以求得方程(6)的解为: (7) 式中:Xn(1≤n<∞)为特征值λn对应的特征函数;特征值λn与材料参数无关;特征函数Xn的形式为: (8) 式中Cn、Dn为常数。 在热流沿相反方向传递的条件下,相当于对方程(2)施加了一个坐标变换:x=l-x,l为一维系统的长度。在此变换下,方程(2)变为: (9) 根据方程(2)的解法可以求得方程(9)的解, (10) 式中: (11) (12) 通过观察方程(2)和方程(9)的形式可以理解时间相关非互易性热传递的含义:即在系统未达到稳态时(∂T/∂t≠0),方程(2)和方程(9)的解不关于x=l/2对称,也就是当热流从左向右传递时的温度分布与热流从右往左传递时的温度分布不对称(如图1所示)。 通过进一步比较方程(2)和(9)的解析解得到,在热导率为常数的前提下,当且仅当ρc(x)≠ρc(l-x)时,系统才能够存在瞬态的非对称热传递现象。因为当ρc(x)=ρc(l-x)时,方程(2)和(9)为完全相同的2个方程,所以只有该不等式成立,非稳态下方程(2)和(9)的解才不相同。因此,在本文条件下,当系统的热导率为常数,具有时间相关的非互易特性的热超构材料存在的充分必要条件是: ρc(x)≠ρc(l-x) (13) 方程(13)作为判定条件表明系统存在时间相关非互易热传递现象的前提条件是密度比热容的乘积函数关于x=l/2不对称。如图1所示,本文中时间相关的非互易热传递系统可以定义为:当热导率κ为常数且满足ρc(x)≠ρc(l-x),在传热系统达到稳态之前的每个时刻,即∂T/∂t≠0时,热流分别从左往右和从右往左传递时的温度分布曲线关于x=l/2轴是不对称的。而当系统达到稳态时,即∂T/∂t=0成立,系统的温度分布与密度比热容的乘积参数是不相关的,在相同热导率下温度分布是对称的,所以系统温度由非稳态到稳态的变化过程即为2条温度曲线由不对称变为对称的过程。这是因为热导率单独影响稳态下的温度分布,而热导率和密度比热容函数综合影响系统达到稳态所需的时间。 图1 时间相关非互易热构超材料示意Fig.1 Schematic diagram of time-dependent non-reciprocal thermal metamaterials 下面根据实际的案例分析时间相关非互易热超构材料的温度分布。以材料纯铜为例,设定系统的热导率为κCu=400 W/(m·K)保持不变,密度比热容乘积函数的形式为线性形式,即ρc(x)=kx+b。定义密度比热容乘积函数的取值范围为[(ρc)Cu/10,(ρc)Cu],即可求得系数值为:k=9ρcCu,b=ρcCu/10。其中(ρc)Cu=3.4×106K/(Jm3)为铜的参数。在模拟中,令T1=280 K,T2=340 K,l=0.1 m,采用线上法(method of lines,MOL)求解方程(2)和方程(9),模拟结果如图2所示。从图2可以看出,在系统未达到稳态之前,2种情况的温度分布是存在明显的非对称性的,在非稳态下 (约0~15 s),系统的温度云图关于中心轴是非对称的,而随着系统达到稳态,温度分布也渐渐的归于对称。在热导率为常数,密度比热容乘积函数ρc(x)=kx+b的分布条件下,热流从左往右传递(图2(b))速率明显大于热流从右往左传递时(图2(a))的速率。因为系统在沿热路径x方向的密度比热容乘积数值是线性逐渐增加的,而密度比热容的乘积越小,传热速率越大,所以热流从左向右传递时,系统达到稳态所需的时间短。 图2 热流分别互逆传递时系统的非互易温度分布Fig.2 The non-reciprocal temperature distribution of the system when the heat flow is transferred in the reverse 为了更加清晰地展示系统的瞬态非互易温度分布特性,取图2中x=l/2处的温度随时间的分布作为参考点,对比研究热流互逆传递时的非对称分布温度随时间的变化规律,其结果如图3所示。 图3 中心点x=l/2处的非互易温度分布Fig.3 Nonreciprocal temperature distribution at the center pointx=l/2 图3中清晰地展示了本文中所设计的热超构材料中心位置的时间相关非互易传热特性。可以看出,在热流传递方向互逆的2种情况下,系统在初始时刻即表现出了明显的非互易性,在热导率为常数的前提下,热流从右向左(ρc(x)=kx+b)的传递速率始终大于从左向右(ρc(x)=k(l-x)+b)的传递速率。同时,热量在密度比热容乘积值小的地方传递得快,在乘积值大的地方传递得慢。图3中,中心点达到稳态时的温度值为(T1+T2)/2=310 K,这是由常数热导率导致的稳态时的线性温度分布所决定的。在求得方程(5),将非齐次边界条件转换为齐次边界条件的过程中,同样运用了该结论。 图4 不同时刻,热流分别互逆传递时的非对称温度分布Fig.4 Temperature distribution of time-dependent nonreciprocal thermal metamaterials at different times when the heat flow is transferred in the reverse 图5 密度比热容乘积函数分布形式对非互易热传递效果的影响Fig.5 Influence of different density specific heat capacity product function distribution forms on non-reciprocal heat transfer 通过以上的模拟可以看出,对时间相关的非互易性热传递超材料在理论上是存在的,下面简单地论述其实验的可行性。非均匀材料参数的构建通常有2种方法,分别为等效介质理论和中性夹杂理论,此处以等效介质理论为例进行说明。使用等效介质理论设计热导率为常数、密度比热容乘积非均匀分布的试验件,至少需要选定3种或3种以上材料,通过调整每种材料所占的配比,在保证热导率不变的前提下,构建出在不同位置上等效密度比热乘积值不同的结构。以A、B、C3种材料为例,假设3种材料的热导率关系满足关系:κA<κB<κC,若想构建热导率为常数的热超构材料,可以选定材料B为基底,通过在材料B上打孔并填充A和C2种材料即可实现,材料A和C所占的体积分数需满足: (14) fA(x)、fB(x)、fC(x)分别为材料A、B和C的体积分数,并满足fA(x)+fB(x)+fC(x)=1。根据方程(14)就可以构建出热导率恒为κB的热超构材料。为构建满足条件的密度比热容乘积函数,还需假设3种材料的体积分数函数分布都为线性分布: (15) 式中a1、a3为实数。对于材料体积分数线性分布的结构,A、B、C3种材料的密度比热容乘积参数仅需满足(ρc)B<(ρc)A,(ρc)C或(ρc)B>(ρc)A,(ρc)C即可构建出密度比热容乘积函数为单调线性的超构材料,线性单调的密度比热容乘积函数形式为: (16) 以上是试验样品的设计分析。通过选择热导率满足κA<κB<κC关系,密度比热容乘积参数满足(ρc)B<(ρc)A,(ρc)C或(ρc)B>(ρc)A,(ρc)C关系,运用方程(14)和方程(15)即可构建出热导率参数为常数,密度比热容乘积函数为线性分布的具有时间相关非互易传热特性的热超构材料。 实验上的测定应该选用灵敏度较高的动态红外热像仪测定结构表面的温度随时间的变化,或者用热敏电阻实时观测沿热传导路径方向的温度信号。 1) 当热导率分布与密度比热容乘积函数分布满足参数失配准则时,在系统达到稳态之前,是存在非互易性的。 2) 当热导率为常数,密度比热容乘积函数不同的分布形式对非互易性的强弱产生影响。当密度比热容乘积函数为线性分布时,其非互易性效果最强。 3) 运用有效介质理论,可以使用3种材料设计热导率为常数,密度比热容乘积函数线性单调分布的具有时间相关非互易传热性能的热超构材料。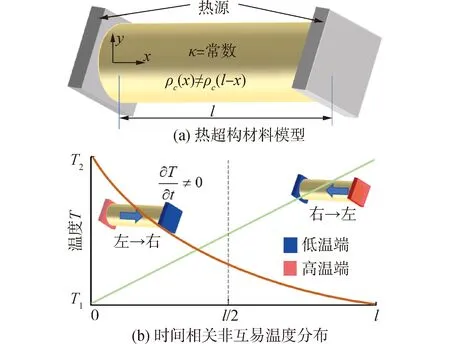
2 时间相关非互易热构超材料的温度分布






3 结论
