准零刚度柔性隔振超结构设计与仿真分析

周佳豪， 潘洪斌， 蔡昌琦， 王凯， 周加喜

(湖南大学 机械与运载工程学院，湖南 长沙 410082)

空天资源的争夺日益激烈，如何减小低频微振动对航天器的指向精度和稳定度的影响一直是该领域不可避免的挑战。例如，NASA的SIM-PlanetQuest计划所开发的光学干涉测量仪，其10 m柔性结构受到来自旋转反作用轮组件的机械振动必须控制在10 nm级；且各类航天器在低频段1～10 Hz抖动量较大，对航天器影响相对高频段更加明显[1-2]。因此，隔离航天精密仪器的低频微振动是提升其工作性能的关键[2-6]。

根据传统的线性隔振理论，若要隔离低频振动，则需降低隔振系统的固有频率。然而，不管是单方面地减小刚度或者增大质量，都会影响隔振系统的稳定性以及承载能力。因此，线性隔振理论无法解决低频隔振问题。随着非线性隔振理论的发展，准零刚度隔振方法得到越来越多的关注。该方法可实现理想的高静低动刚度特性，不仅能隔离低频振动，还能承受较大的负载，可有效地解决低频隔振问题[7-8]。

准零刚度是指系统在平衡状态时的动刚度很小甚至为零，其实现方法主要有2种：1)利用传统的正负刚度构件并联，通过正负刚度相互抵消达到准零刚度；2)通过柔性常力机构在弹性变形时产生准零刚度特性[9-10]。相对于利用多个元件组合实现准零刚度，第2种方式所需零部件极少，且利用一体化设计和增材制造技术加工能有效减小装配误差。

近年来，研究人员提出了多种多样的准零刚度结构，以下列出几种具有代表性的准零刚度结构。Carrella 等[11]提出了经典的三弹簧模型，由作为承载的正刚度线性弹簧以及2根提供负刚度的斜弹簧构成。Liu等[12]和Sun等[13]利用磁力弹簧替代负刚度元件来实现准零刚度特性，减小了构件之间的摩擦所带来的误差。Shaw等[9]通过线性弹簧与复合双稳态板并联构造了一种准零刚度隔振器，结果表明，相比等效的线性系统有着更低的起始隔振频率和更低的响应峰值。Xu等[14]提出了一种由倾斜连杆与水平磁弹簧并联组成的准零刚度隔振器，研究结果表明，准零刚度隔振器在低频区域隔震效果远远优于线性隔振器。Zhou等[15]将2个凸轮-滚子-弹簧机构和一个线性弹簧并联构成准零刚度隔振系统，此研究使准零刚度结构紧凑化。此外Sun等[16-17]提出了X形结构准零刚度隔振系统。

单层准零刚度隔振系统虽然能够有效地隔离低频甚至超低频振动，但是效果还无法满足精密仪器的隔振要求。若能对振动进行多次衰减，隔振效果必定能够得到提升，由此多层准零刚度隔振应运而生。Wang等[18]提出了一种利用凸轮-滚子-弹簧机构实现的2层准零刚度隔振系统，结果表明其在单层的基础上显著提升了隔振效果。Chai等[19]设计了一种新型的2层准零刚度隔振器，结果表明相对于相应的2层线性系统，2层准零刚度隔振系统有着更低的起始隔振频率以及更加优异的隔振性能。Deng等[20]提出了多层准零刚度隔振系统，不仅有效地提高了隔振性能，并且明显拓宽了准零动刚度位移区间的有效范围。

然而，利用多个正负刚度元件所构成的准零刚度系统难以避免装配误差，若利用传统准零结构进行多层叠加，安装精度将严重恶化隔振性能。对多段梁进行优化设计可获得柔性常力机构，并实现准零刚度特性[10]，一体化加工不仅极大地减少了刚度元件的数量，而且避免了正负刚度元件并联导致的安装误差。因此，可利用柔性恒力结构设计多层准零刚度低频隔振超结构。

本文首先利用形状优化方法设计了单层准零刚度柔性结构，然后基于大变形理论结合打靶法，分析了柔性结构的静力学特性，并利用有限元仿真进行了验证。将单层准零刚度柔性结构按竖向堆叠构造了多层准零刚度柔性隔振超结构，建立了其有限元模型和多自由度简化模型，研究了其隔振特性，并讨论了阻尼和层数对隔振性能的影响。

1 单层准零刚度柔性结构设计

1.1 设计方法

单层准零刚度柔性隔振结构如图1(b)所示，其主要由2部分组成：1)作为承载平台的上下多边形环片；2)位于上下相邻环片中间的12片具有准零刚度特性的柔性多段梁，如图1(b)所示。隔振结构在受到沿纵向(z轴的负方向)不同压缩量时，表现出不同的刚度值，特别是当压缩量在某个区间内时，其刚度值接近于零刚度，即准零刚度。

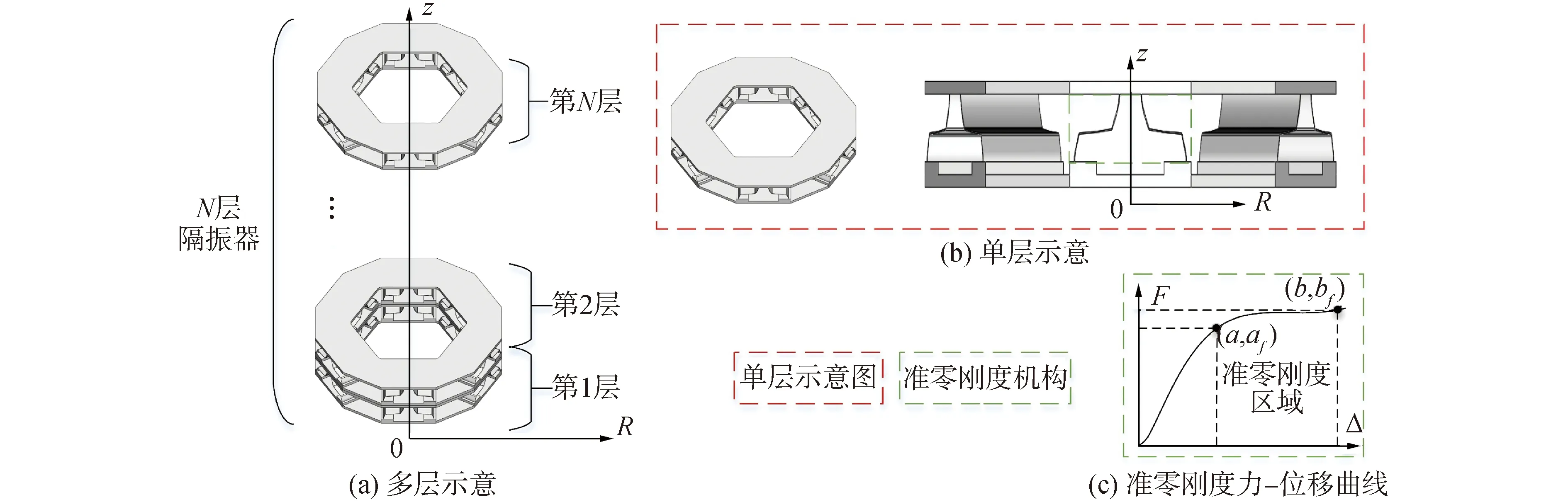
图1 准零刚度柔性隔振结构示意Figure.1 Schematic diagram of quasi-zero stiffness flexible vibration isolation metastructure

多段梁的力-位移关系如图1(c)所示。为在准零刚度设计区间[a,b]实现准零刚度特性，即力-位移曲线在(a,af)点到(b,bf)点的范围内应尽可能平坦。在准零刚度设计区间内，将最小的力除以最大的力定义为平坦度(平坦度=Fmin/Fmax×100%)。在刚度为零的情况下，最小的力等于最大的力，即平坦度为1。因此多段梁的设计目标是在准零刚度设计区间内使平坦度与1的偏差最小化。

1.2 多段梁的优化设计

单层结构如图1(b)所示，其主体结构为具有准零刚度特性的多段梁。由于单层隔振器是由12片相同的多段梁周期排布所组成，因此仅需取其中一片多段梁进行设计优化即可。如图2中的虚线框所示，多段梁被限定在一个尺寸为Lx×Ly的矩形设计区域内。多段梁被节点n2和节点n3分成3段，节点n1和n4是多段梁的首末两端点，固定于设计区域的边界，而节点n2和n3处于设计区域，其坐标是设计变量。

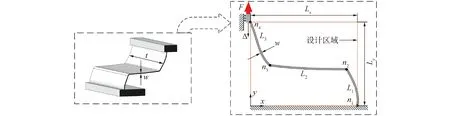
图2 优化设计变量和设计边界示意Figure.2 Schematic diagram of optimized design variables and design boundaries

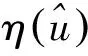
(1)

式中：ci0、ci1和ci2是待定系数。基于形状描述方程，可以给出每段梁上各个点的坐标(Lxi,Lyi)：

(2)

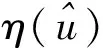
多段梁结构优化设计的优化目标以及约束条件：

(3)

其中，约束条件g1与g2要求多段梁上的每个点的位置不超出设计区间，确保优化后多段梁整体都处在设计区域内；约束条件g3要求每段梁不会出现自我交叉现象；约束条件g4与g5保证多段梁的连续性；约束条件g6要求多段梁在变形过程中最大应力在材料许用应力范围内。优化输出结果为节点n2与节点n3坐标位置以及每段梁的形状描述方程系数ci0、ci1和ci2(i=1,2,3)。

利用Matlab中的fmincon函数求解式(3)的优化问题，并在优化求解过程中利用广义打靶法求解多段梁的变形。如表1所示为优化计算过程中的已知参数，在本文中多段梁优化设计所用材料为聚乳酸(PLA)。优化结果如表2所示。

表1 已知参数Table1 Known parameters

表2 优化结果Table2 Optimization results

获得优化结果后，进一步计算优化后多段梁的力与位移关系。由于多段梁的大变形过程属于边值问题，可以利用广义打靶法进行求解，结果如图3所示。由图3(a)可以看出在准零刚度设计区间4～9 mm位移范围内力与位移曲线较为平坦，满足设计要求。由图3(b)可以看出在4～9 mm位移范围内刚度较小甚至等于零，进一步验证了优化结果满足设计要求。

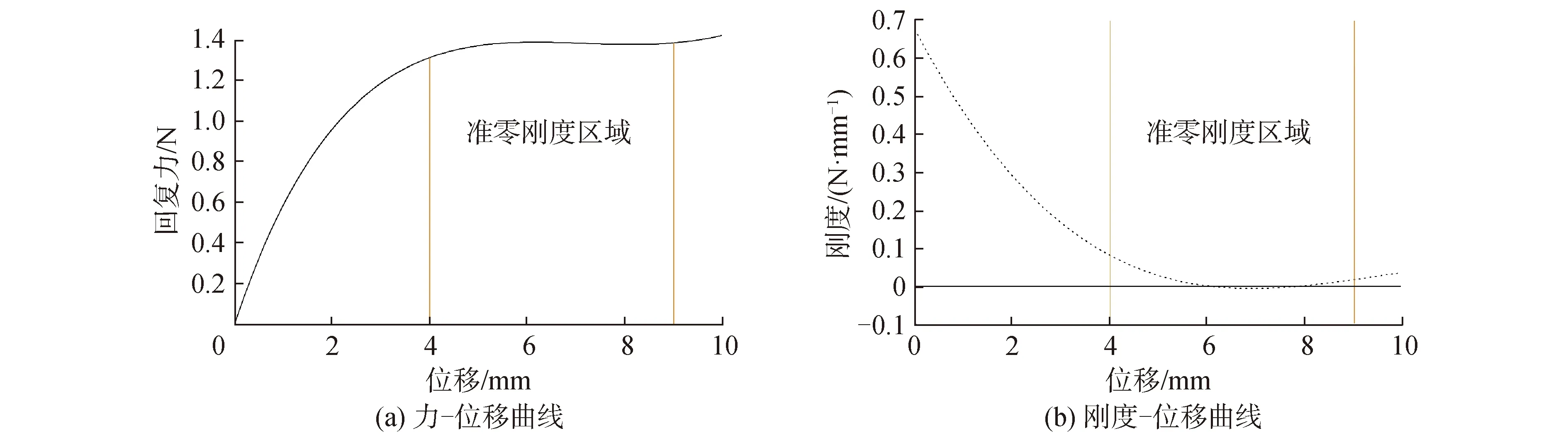
图3 优化结果显示Fig.3 Optimization results showing

1.3 单层柔性隔振结构的刚度特性

基于上节的优化结果建立单层柔性隔振结构的有限元模型，如图4(a)所示，并对其进行静力学仿真。由于每个单层结构都由12片相同的多段梁并联组成，则叠加12片相同多段梁的回复力记可得到单层柔性隔振结构的回复力。

由图4(b)所示回复力与位移关系可以看出，考虑材料泊松比时仿真计算所得单层准零刚度隔振器回复力大于打靶法计算所得回复力。若不考虑材料泊松比，有限元仿真与打靶法计算结果基本吻合。由此可看出材料泊松比是打靶法计算与有限元仿真计算误差的主要影响因素，也为后续试验结果的误差分析提供了理论依据。从图4(b)看出回复力-位移曲线存在平坦区域，并且图4(c)所示3条刚度曲线都存在刚度为零或接近于零的区间。综上所述，此单层柔性隔振结构可以实现准零刚度特性。

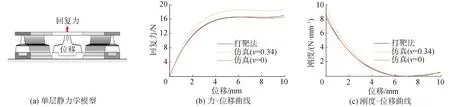
图4 静力学结果对比 (v为泊松比)Fig.4 Comparison of statics results (v is Poisson′s ratio)

2 多层准零刚度柔性隔振超结构

2.1 建模与动力学分析

将单层准零刚度柔性隔振结构沿竖向周期性堆叠，构造多层准零刚度柔性隔振超结构，如图5所示。将图5(a)中所示超结构简化为图5(b)中所示的多自由度动力学模型，每一层包含相应的等效刚度与等效阻尼。其中，xp为超结构所受位移激励；xi为每一层的绝对位移；mt为被隔振质量m0与承载平台质量mu之和，md为单层柔性结构的质量。通过数值求解多自由度运动方程，计算小振幅谐波激励下的有限层数的动态响应。

由N个单层准零刚度柔性结构组合构成N层准零刚度柔性隔振超结构，并假设结构仅沿纵向振动，如图 5(b)所示。据图5(b)中虚线框区域所示模型，可列出第i层准零刚度柔性结构的动力学方程，如式(4)中第2项所示；由于第1个和第N个单层准零刚度柔性结构受力情况不同于中间层单层准零刚度柔性结构，故在此单独列出其动力学方程式(4)第1项与式(4)第3项。N层准零刚度柔性隔振超结构动力学方程组为：

(i=2,3,…，N-1)

(4)

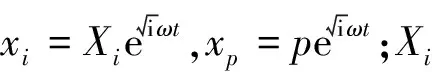
图5 动力学计算模型Fig.5 Dynamic calculation model

将谐波响应xi表达式以及位移激励xp表达式带入式(4)中求解可得稳态响应的位移幅值表达式：

(5)

式中：Ku为刚度矩阵；Cu为阻尼矩阵；Mu为质量矩阵；Xu=[X1X2…XN]T为位移向量；F=[F00…0]T为激励向量，且F0=k1p+c1ωp。

进一步，利用传递率来评估隔振器性能，具体表达式为：

(6)

取m0=0.8 kg,mu=0.066 kg,md=0.159 kg，刚度取值如表3所示，激励频率取0～100 Hz利用式(6)计算不同阻尼比情况下1层、3层、5层、7层柔性隔振结构的传递率曲线。

表3 不层数超结构刚度取值Table3 Stiffness value of non-storey superstructure N/m

由图6可知，对1、3、5、7层分别逐次取阻尼比为0、0.01、0.05、0.1依次进行计算。结果表明随着阻尼增加，在高频区域共振峰值逐渐减小甚至变为光滑的曲线；在低频区域效果远远没有在高频区域明显。因此，选择适当的阻尼可以有效改善隔振效果，甚至能够有效的降低起始隔振频率。

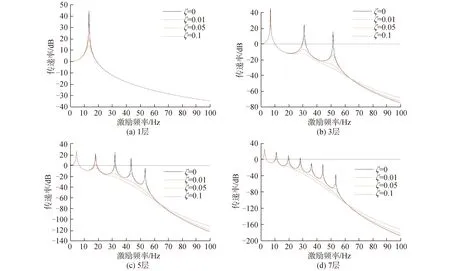
图6 不同阻尼比下理论计算传递率Fig.6 Theoretical calculated transmissibility under different damping ratios

2.2 有限元仿真验证

如图7所示，利用有限元方法建立多层准零刚度柔性隔振超结构的分析模型，并对结构进行动力学仿真分析。分别对1层、3层、5层、7层建模并给定相应边界条件进行求解，计算位移传递率，验证理论分析结果。材料选用聚乳酸，其材料参数为：弹性模量E=3.15 GPa、泊松ν=0.34、密度ρ=1.24×103kg/m3。设置与数值计算相同的激励幅值p与频率范围0～100 Hz，选择直接稳态动力学求解方法。拾取每种情况下顶部位移幅值Xt为隔振质量位移计算模型振动传递率表达式为：

(7)

图7 1、3、5、7层动力学仿真模型Figure.7 Dynamic simulation model of layers 1, 3, 5 and 7

利用数值方法与有限元仿真分别对1层、3层、5层、7层超结构隔振效果进行计算求解，取无阻尼情况计算，结果如图8所示。由图8 可以看出理论分析结果与有限元仿真分析结果高度重合，验证了理论模型的正确性。由图8还可看出，在传递率有效隔振频率区间内，随着层数的增加，隔振效果显著提升；而且多层隔振超结构随着层数的增加共振峰的位置也随之向低频移动，起始隔振频率也随之向低频移动，这与理论分析结果也完全一致。需要注意的是，随着层数增加，共振峰越来越多，对于低频区域内的隔振效果有一定影响。根据上节理论分析结果，适当增加系统阻尼可有效抑制低频区域的共振峰，从而提升其隔振性能。

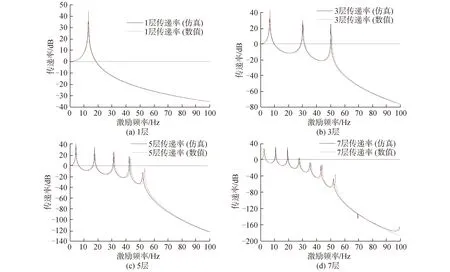
图8 动力学理论计算与仿真结果对比Fig.8 Comparison of dynamic theoretical calculation and simulation results

3 结论

1) 利用打靶法分析了单层准零刚度柔性隔振结构的静力学特性，并利用有限元仿真进行了验证，结果表明2种方法结果高度重合，且验证了其准零刚度特性。

2) 在相同的隔振质量与激励条件下，在有效隔振频率区间内，多层隔振超结构随着层数的增加，隔振效果显著提升；而且随着层数的增加共振峰的位置也随之向低频移动，起始隔振频率也随之向低频移动。

3) 理论分析结果表明，适当增加系统阻尼可有效抑制低频区域的共振峰，且起始隔振频率向低频移动。