周期结构振动带隙特性优化研究进展

熊远皓， 李凤明， 张传增

(1.哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001； 2.德国锡根大学 土木工程系，德国 锡根 D-57068)

振动是一种常见的自然现象，在生活中无处不在。有害的振动会影响设备的正常运行和人们的生活环境，有时甚至会威胁工作人员的生命安全，因此振动控制在各个领域的需求越来越高。振动通常是以弹性波的形式在介质中传播[1-2]，其本质上是在结构/材料中的弹性波传播以及弹性波与周围介质的耦合作用，因此对弹性波的调控机理及其特性的研究，是振动控制的核心问题。目前，振动控制主要有3种方法：1)控制产品动态性能，设计和制造产生较小振动的产品；2)主要通过衰减、隔离等方式来控制振动传播；3)对振动所影响的目标(仪器设备或者人体)进行保护，减弱振动对其影响。随着人们对产品功能的要求越来越高，产品结构也越来越复杂，减小振动源头也越来越困难，而受振动影响的对象经常是不固定的。因此使振动在传播过程中衰减或隔离来控制振动成为解决这一系列问题的主要方法。

1 振动带隙特性

周期结构(声子晶体或超材料结构)能利用自身几何/材料的特殊设计产生弹性波带隙，以达到减振降噪的目的[3-6]。目前振动带隙产生的机理主要有Bragg散射机理[7-9]及局域共振机理[10-12]。Bragg散射机理主要是由于几何/材料的周期性，导致弹性波在某些频段内不能在结构中传播从而产生带隙，带隙位置主要受Bragg条件限制，因此这类带隙被称为Bragg带隙，此类带隙衰减能力较强且设计易于在中高频实现[13-16]。局域共振机理主要依赖单元本身的谐振特性而非周期性，带隙频率与共振单元的固有振动特性关系密切，所以此类带隙称为局域共振带隙，此类带隙在低频减振方面效果显著[17-21]。2类典型的带隙特性如图1和图2所示。

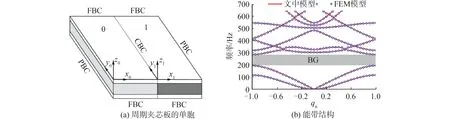
图1 Bragg周期夹芯板的带隙特性[18]Fig.1 Bragg band-gap characteristics in the periodic sandwich plate [18]

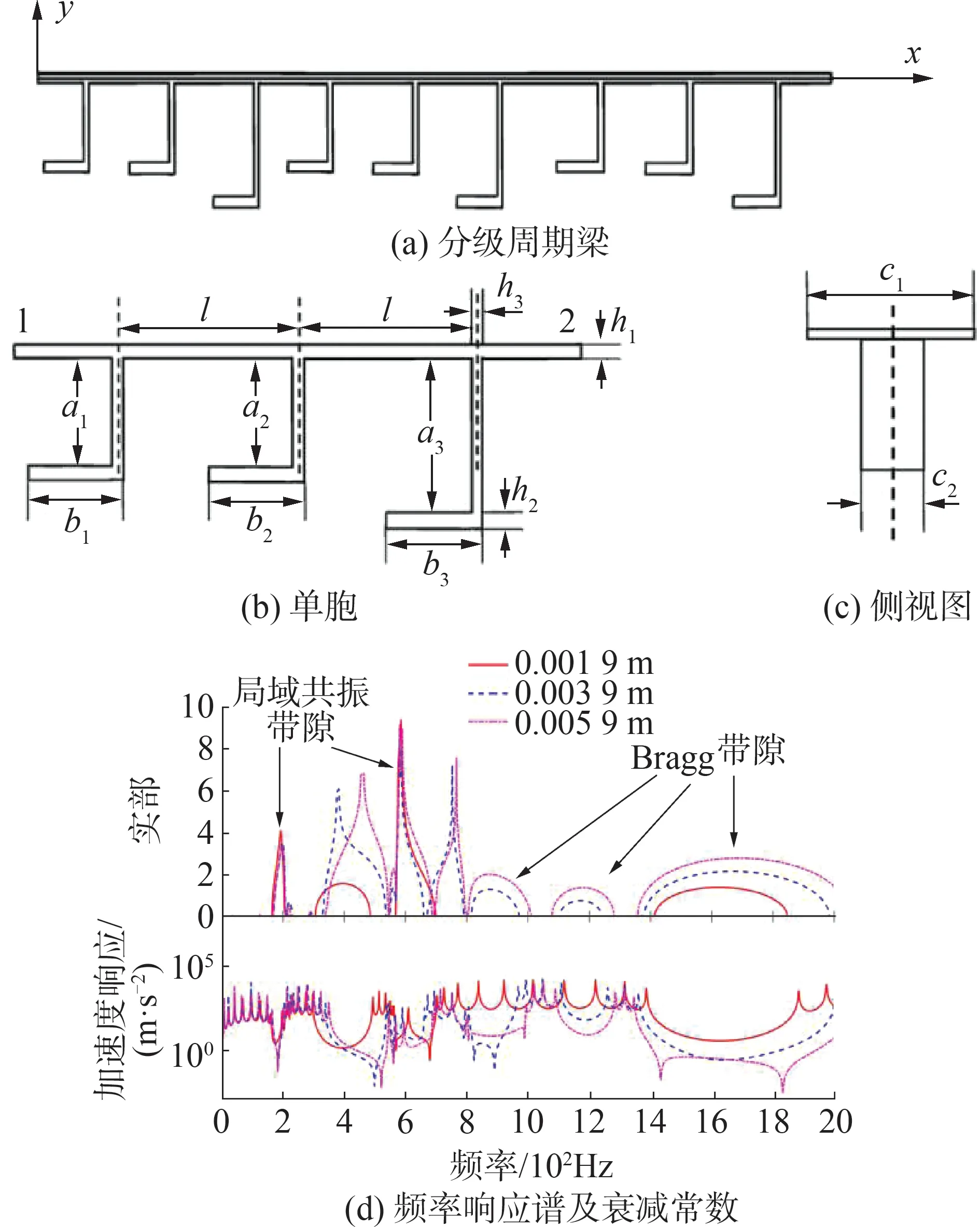
图2 分级周期梁的局域共振带隙特性[21]Fig.2 Local resonance band-gap characteristics in the hierarchical periodic beam[21]

尽管针对周期结构振动带隙特性的研究已经取得了许多进展，然而如何能够使这些结构更好地发挥其带隙特性以适应实际需求仍为当下的研究热点，因此对此类结构的带隙特性优化研究便应运而生[22-26]。“优化”的原理是按照特定的目标，对需要优化系统的构成因素及关系进行选择、设计和调整，使其能够达到最优效果。因而将所需带隙的位置或者宽度作为优化目标，通过对已有的几何和材料参数等方面进行调整，使之达到优化设计要求，便是振动带隙特性优化的意义。优化后的结构能够符合特定的减振隔振需求，因此大大提升了此类结构在工程实践中的应用效果，因此对于此类结构的带隙特性优化研究一直热度不减[27-30]。

2 振动带隙特性优化方法

目前可以运用的优化算法很多，例如遗传算法、粒子群算法、人工神经网格以及渐近线法等。在振动带隙特性的优化研究中，遗传算法是较为常用的优化工具[31-33]。Hussein等[34]利用多目标遗传算法，设定了多个优化目标，以单元中的层数和每层的厚度作为优化参数，对一维周期层状材料结构的振动带隙特性进行了拓扑优化，获得了同时实现通带和禁带优化目标的分析结果，如图3所示。

从图3中可以看出，通过遗传算法优化后，在相同铺设层数情况下，2种最佳设计产生的带隙衰减特性有了明显提升。在此基础上，进一步对铺设层数进行优化，可以看出选择12层铺设层数时的带隙衰减能力比10层时的衰减能力更强。这一研究结果充分说明了遗传算法可以用于周期结构的带隙性能优化。此后, 他们又将这种优化方法应用到了周期性复合材料当中，设计了一种方形的双重材料单胞，将这种周期结构的最大带隙宽度与带隙相对于每个带隙的中心频率进行了归一化，经过优化后的结构表现出了宽频带隙特性[35]。这些研究推动了利用遗传算法优化振动带隙特性的工作，此后，越来越多的学者将遗传算法运用于周期结构带隙特性优化的研究当中[36-39]。

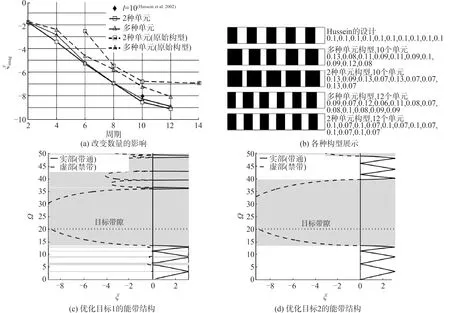
图3 单胞厚度和铺设层数优化及优化后的色散曲线[34]Fig.3 Optimization of the unit-cell thickness and layer number, and the optimized dispersion curves[34]

Koutsianitis等[40]提出了一种采用分流压电回路增强生长微结构的带隙特性，考虑机电耦合系数的最大限度，利用遗传算法优化设计了谐振分流电路的最佳参数从而获得了最佳带隙，如图4所示。从优化前后的对比结果可以看出，优化前结构带隙位于30～40 kHz的高频段。设置分流压电回路后，带隙位置降低到10 kHz以内，并且在3.2～10 kHz的带隙占比很大，同时还在2 000 Hz附近出现了一个较窄的带隙。这对于此类结构的实际应用提供了更多的途径，优化后的微结构可以应用于具有相对较低减振频率的需求中。

Qiu等[41]对手性超材料从概念到具体细节设计进行了优化，实现了在有限应变条件下具有特殊泊松比的手性超材料设计，并采用移动渐近线方法和遗传算法得到了最优构型。Zhang等[42]设计了一种新型含有十字型孔洞的声子晶体，基于遗传算法优化了其在低频范围内的振动带隙特性，引入了磁流变弹性体以优化空间磁场分布，分析了磁场对带隙的影响。Garus等[43]利用遗传算法优化了一种准一维声子晶体涂层在超声频率范围内的带隙特性。Xie等[44]基于稀疏点采样的切比雪夫多项式展开方法研究了声子晶体中的不确定性对带隙特性的影响，并引入遗传算法进行了带隙特性优化。Dong等[45-46]采用遗传算法对二维非对称声子晶体和双负声学超材料进行了优化，提高了计算效率，获得了良好的优化结果，并通过实验验证了其可行性。

除了遗传算法之外，还有许多其他优化方法也被应用于振动带隙特性的优化研究中[47-49]。基于频谱特性，Morini等[50]研究了一种采用斐波那契(Fibonacci)规则生成基本单元的周期双分量声子晶体杆的动力学特性，并优化了其带隙特性，以实现低频带隙。Rong等[51]设计了一种非共振双曲弹性超材料如图5所示，采用基于其物理性质的梯度优化，通过2步拓扑优化方案，使其具有较宽的带隙频率范围，并且用数值方法证明了其具有负折射、偏折射、超分辨率成像等新颖特征。

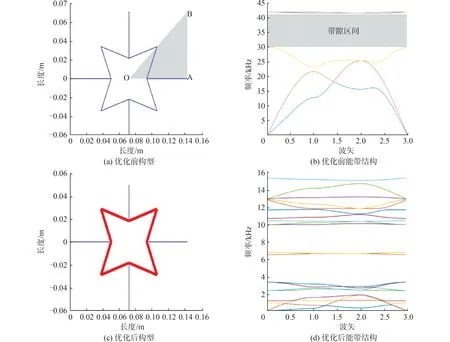
图4 利用分流压电回路优化生长微结构的带隙特性[40]Fig.4 Optimization of shunted piezoelectric patches on the band-gap characteristics of auxetic microstructures[40]

Zhou等[52]设计并分析了一种周期铺设有梁型谐振器的可调谐超材料梁结构，将压电分流阵列技术应用于每个谐振器，从而可以对其带隙特性进行主动调节，并以此为基础优化了超材料梁的减振性能，使其能够产生与Bragg带隙效果相当的较宽低频带隙。Nguyen等[53]利用等几何分析和参数化水平集方法设计材料微观结构，将变量设计成与控制点相关联的水平集并从优化器中进行求解，降阶模型进一步提高了每次迭代的计算效率，其数值结果表明了这种优化方法的有效性。Noguchi等[54]和Nishi等[55]利用基于水平集的拓扑优化方法设计了一种双曲色散单元，控制高频电磁波在周期微结构内的传播，分别以2种优化问题为例进行了分析，并与标准有限元分析方法进行了比较，验证了该优化方法的有效性。

3 振动带隙特性优化研究进展

在关于周期结构的振动带隙优化研究中，可以设置不同的优化目标与优化方向，例如：优化结构的构型、优化结构中的材料组分、优化不同结构之间的排列组合顺序等。由于带隙的产生及其特性与结构本身的构型、材料和周期排列等设计密切相关，所以无论是Bragg带隙或者局域共振带隙，都可以通过改变周期结构单元的设计来调控其带隙特性[56-62]。

Wang等[63]研究了在二维硅板上定期更换排气孔的声子晶体谐振器，并且利用实验验证了仿真结果的正确性，在实验中还发现，2种谐振器的谐振频率、品质因子以及能量损耗具有不同的优化条件。Soe-Knudsen[64]利用Floquet理论，设计了一种由弯管和直管组合的周期管道系统，并通过形状优化函数对其进行了优化，优化的目的在于，使得结构产生的振动带隙在一个特定的频率范围内，如图6所示。分别针对175～375 Hz及325～525 Hz 2个优化带隙位置的优化目标，对周期管道系统的单胞构型进行优化。从图6中可以明显看出，在不同的单胞构型时，两者产生的振动带隙位置是不同的。这样的优化使得结构具有不同的几何构型，适应不同特定频段内的减振需求。Xin等[65]设计了一种新型六边形纽带手性结构，如图7所示。这种六边形纽带手性结构的单胞大小仅为20 mm，但其产生带隙的位置相比于其他同体积大小单胞所产生的带隙位置频率更低，优化后的能带结构表明，在1 900 Hz～4 500 Hz位置可以出现很宽的振动带隙，并且在相对低频的1 000 Hz以内也有带隙产生。

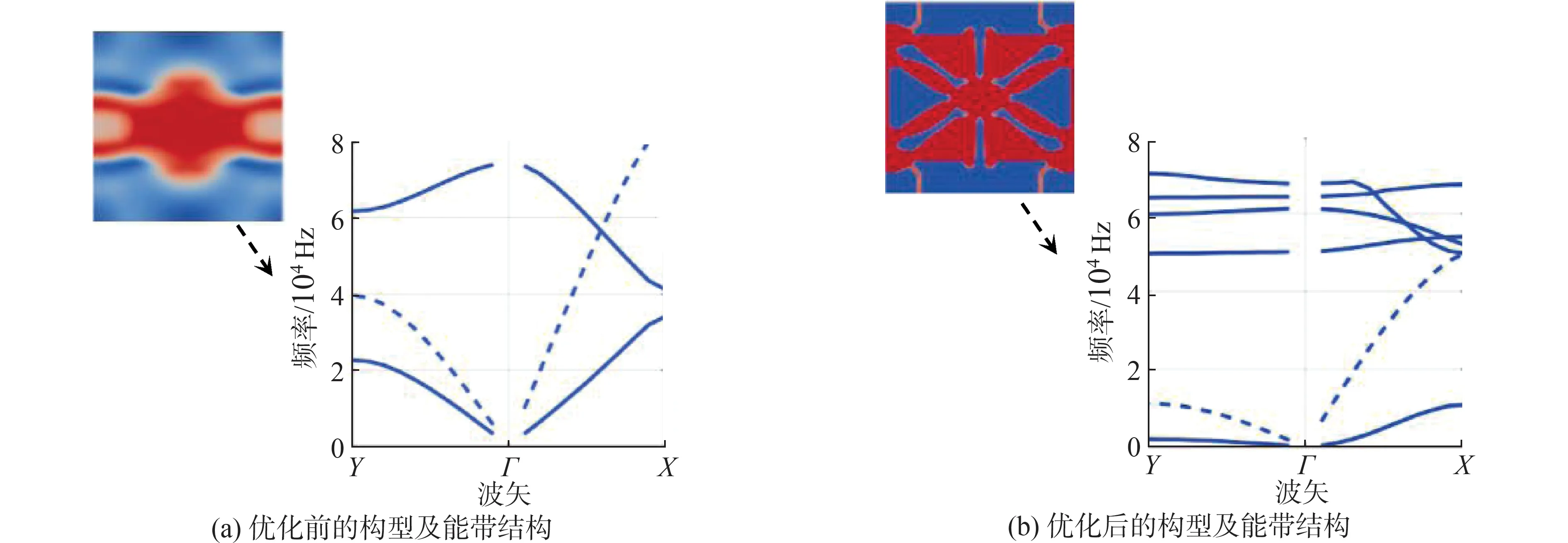
图5 未优化和优化后的单元及能带结构[51]Fig.5 The unoptimized and optimized units and band structures[51]

Guo等[66]基于质量惯性矩设计了锯齿形梁支撑的阶梯式声子晶体，并对其振动带隙特性进行了优化。他们不仅仅关注结构的构型以及尺寸参数，同时也关注使用不同材料组合构成的单胞对振动带隙特性及优化效果的影响。研究表明，优化后的第1个带隙宽度增加了17.25 kHz，提升了60%。Yang等[67]设计了一种由均匀材料组合而成的晶格结构，研究了包含最优几何缺陷的完美晶格结构的最大带隙宽度和线性几何缺陷波导的可调性，利用有限元法计算了不同几何参数结构的色散曲线，并采用理论建模验证了仿真结果的正确性。研究结果表明，可以通过设计最优几何结构实现不同阶的最宽带隙，而合理利用缺陷参数的改变，可以有效地控制其波导特性。

Gasparetto等[68]提出了考虑特定弹性力学性能以及声子滤波能力的晶格材料，并将桁架微观几何参数作为设计变量进行多目标和多尺度优化。采用Floquet-Bloch定理进行带隙特性分析，同时利用 Cauchy-Born假设和宏观均匀性的 Hill-Mandel原理预测了其力学性能，发现了带隙长宽比与晶格宏观力学性能之间的关系。LYU等[69]以声学超材料的多功能性为设计出发点，采用有限元法研究了由三角形单元组成的拉伸主导热膨胀超材料，提出了一种由多频率范围内外部温度变化调节超材料带隙特性的设计方法。结果表明，以拉伸为主的热膨胀材料在实现温度变化的同时，不仅具有不同的特性，还能保持原有的定制热膨胀性能，通过合理的材料选择和结构优化，能够实现热膨胀系数的可定制性和带隙的可调性，如图8所示。

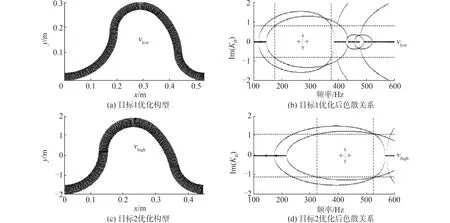
图6 2种不同优化目标的构型及优化后的色散关系[64]Fig.6 The configurations obtained for two different optimization objectives and the optimized dispersion relations[64]

Goh等[70]设计了一种同时考虑P波和SV波的工程弹性超材料，通过超材料单元逆向设计的思路，将设计问题转化为一个优化问题。研究结果表明，采用窄周期性的超材料单元组件，能够达到所期望的带隙效果，这种处理方式也可以用于波转向、波屏蔽及波控制等研究中。Li等[71]基于图像的有限元和深度学习的辅助，提出了数据驱动的声子晶体设计方法。采用有限元分析研究了优化对象的带隙特性，通过训练多层感知器建立带隙特性与拓扑特征之间的联系，训练完成后可以用于设计具有预期带隙的声子晶体。这种方法也可以进一步拓展到其他各种具有特定功能需求的机械结构设计的优化研究中。材料的不确定性空间变化，会显著影响声子晶体的带隙特性，因此Zhang等[72]研究了考虑随机场材料结构性能来设计声子晶体微观结构的鲁棒拓扑优化方法。在此过程中，材料性质的空间分布先用一个随机场表示，利用展开最优线性估计法离散成独立变量，采用多项式展开进行随机带隙的分析，在此基础上再进行优化。研究结果表明，该方法能生成具有较大宽度和较低灵敏度带隙的最优结构。Chu等[73]提出了基于非对称双锥外轮廓的五模超材料，利用有限元法计算了其带隙特性，并扩展到三维结构。通过调整双锥的外轮廓及直径可以减小结构的对称型以拓宽带隙。研究表明，经过对称性优化后，最大相对带隙宽度扩大了15.14倍。Hong等[74]利用改进的波有限元法，有效预测了周期加强壳结构的振动带隙特性，并结合遗传算法对其进行优化，可以获得在气动载荷条件下整个结构的最佳带隙。研究表明，优化加强筋的几何参数能使面外振动在所需频率范围内显著衰减。

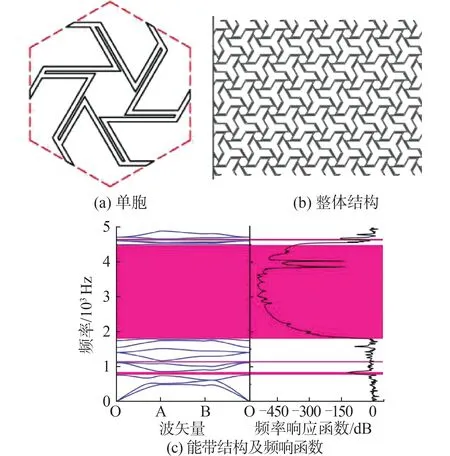
图7 六边形纽带手性结构单胞，整体结构和优化后的能带结构[65]Fig.7 The unit-cell , the whole structure , and the optimized band structures of the six-ligament chiral structure[65]

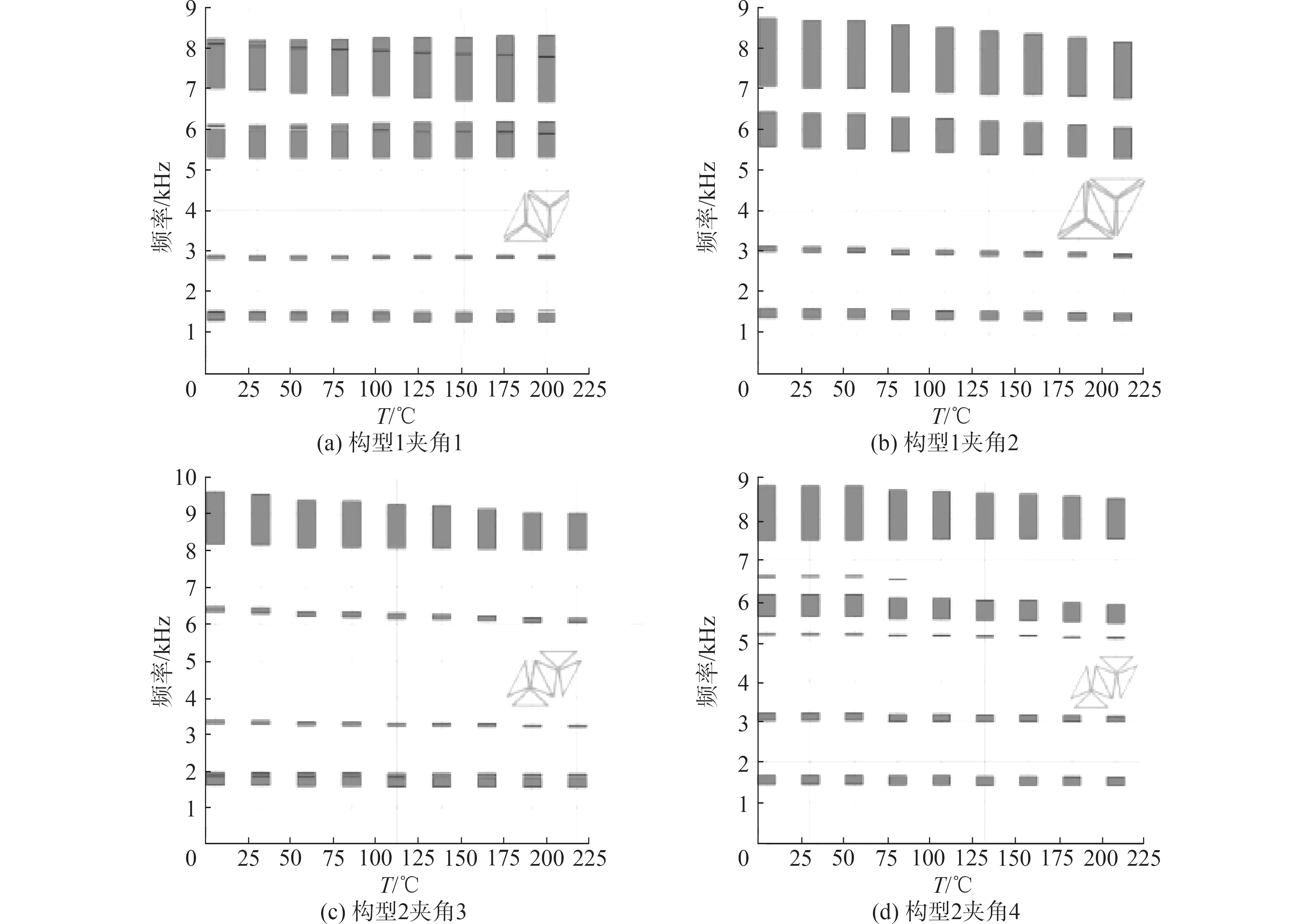
图8 不同单元的带隙与优化参数(内部夹角)的关系[69]Fig.8 The relations between the band-gaps of the different units and the optimization parameters (angles in the units)[69]

随着科学技术的不断发展，对低频减振的需求也日益增加，因此许多学者十分重视低频振动带隙特性的优化[75-77]。Chen等[78]设计了一种如图9所示的地震超材料结构，基于声子晶体的概念，由立方体单元周期性排列构成了超材料结构，这些单元由橡胶涂层、钢和软基体构成。分析表明，这种超材料结构能够在0～20 Hz的频率范围内产生宽度为8.5 Hz的低频带隙。Sun等[79]设计并研究了六角形和Kagome单元的分层蜂窝超材料结构，分析了2种类型中完全填充散射体的影响和带隙产生机制，并通过遗传算法对散射体填充方案进行优化，以得到超低频带隙。优化后的晶格在低频段展现出极宽的带隙，并通过实验验证了计算结果的正确性。Xin等[80]设计了阶梯式混合框架柱状声子晶体，与传统的声子晶体相比，这种设计能够产生低频的完全带隙，为低频区域声子晶体振动带隙特性优化提供了一种可实现的结构。

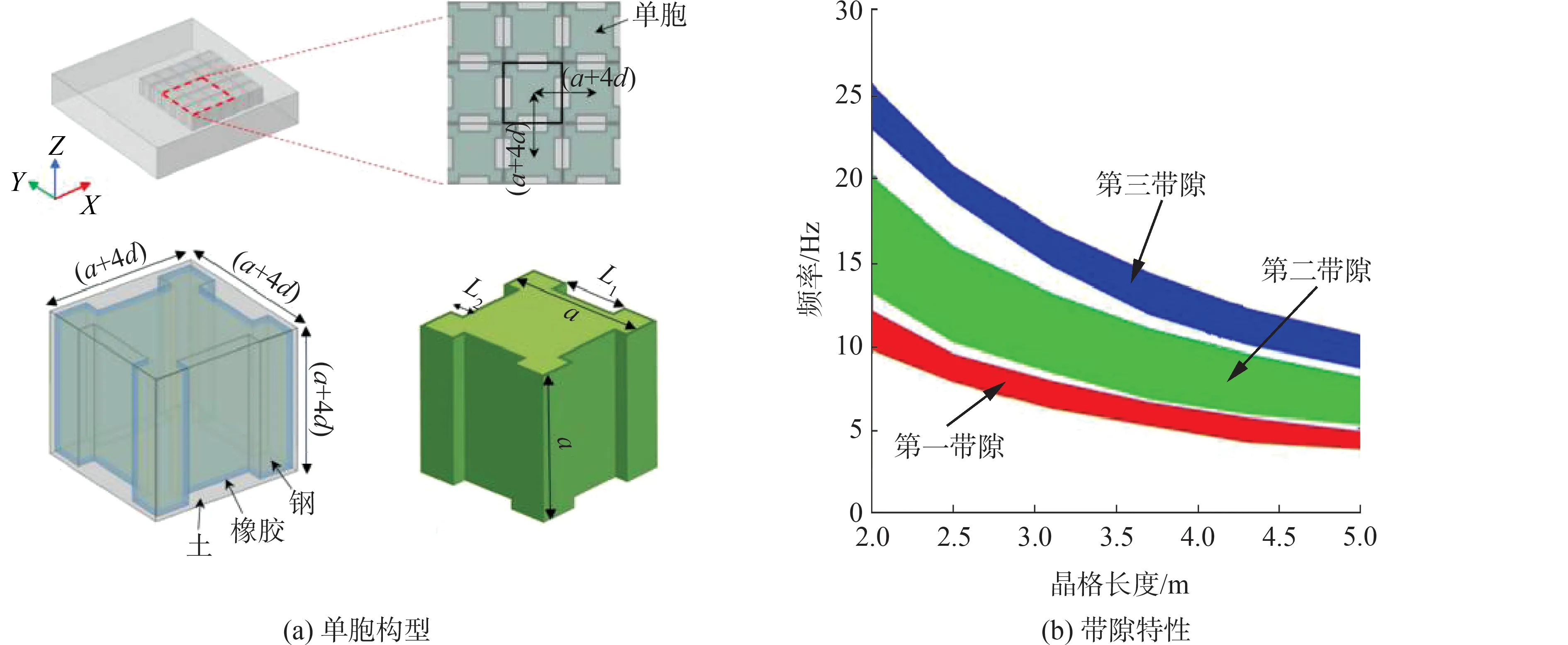
图9 地震超材料以及不同带隙与优化参数的关系[78]Fig.9 The seismic metamaterial and the relationships between the different band-gaps and the optimization parameter[78]

Zhang等[81]研究了由嵌入在磁流变和电流变弹性体中的弹性基体组成的声子晶体的弹性波传播特性，给出了带隙随电场和磁场变化的规律。研究发现，电场和磁场可以有效地调节带隙，并且可以通过优化电场和磁场以获得最优带隙结果，进一步研究发现，在结构上钻孔可以使带隙向低频移动。Shao等[82]根据局域共振理论，设计了蜂窝声子晶体以获得更宽的低频带隙。研究表明，改变铁芯的高度能够调节其能带结构和带隙位置，根据不同的阻尼要求进行优化，可以得到不同种类的蜂窝声子晶体。Cheng等[83]为了拓宽和控制低频带隙，提出了基于方格填充材料的新型结构，并利用改进的遗传算法优化了材料的空间分布。优化后在300 Hz以内有多个完全带隙出现，并且第一个带隙频率位于50 Hz附近，且带隙在整个频率段内的占比很大，这为低频带隙特性优化提供了一种新的思路。Xiong等[84]设计了一种包裹橡胶薄膜的半球式谐振子周期超材料板，通过振动实验验证了这种设计的可行性，并利用渐近优化的方法对特定的减振频段进行了带隙特性优化，如图10所示。从优化前后能带结构的对比可以看出，优化后的带隙不仅满足带隙频段的要求，还极大拓宽了带隙的宽度，而且在30 Hz附近出现了新的带隙。

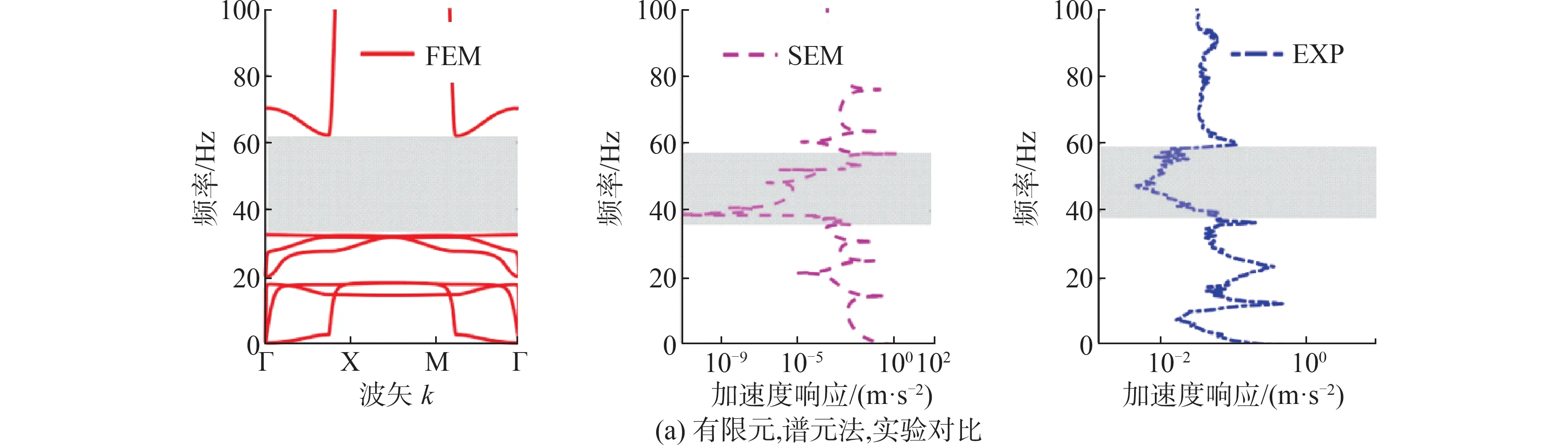
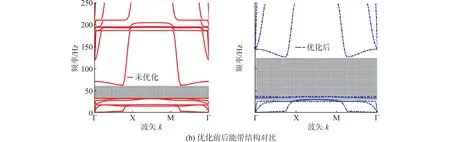
图10 周期超材料板的带隙特性实验验证以及优化前后能带结构对比[84]Fig.10 The experimental validation of the band-gap properties of the periodic metamaterial plate, and the comparison of the unoptimized and optimized band structures[84]

4 结论与展望

本文综述了周期结构振动带隙特性优化的研究进展。针对周期结构(声子晶体或超材料结构)的振动带隙特性经过数十年的研究发展，已经取得了丰厚的研究成果，积累了相当丰富的研究经验，在此基础上进行的带隙特性优化研究起到了对传统结构性能的提升作用，但仍有一些可以深入研究的方向有待于进一步探索。

从现有的研究成果可以看出，对于中高频段的振动带隙特性优化已经有了显著进展，并且可以通过不同的优化手段得到良好的带隙效果，能够面对不同的使用环境选取合适的优化策略及优化参数。但对于低频特别是超低频的振动带隙特性优化研究成果依然较少。尽管目前仍有不少学者从事周期结构带隙宽度的优化研究，通过合理选取和使用现有优化方法，能够取得良好的效果，但对带隙位置(尤其是对于低频带隙)的精确优化研究成果还是比较缺乏。然而在实际工程应用中，降低特定频带内的振动或许更有需求，因此对于带隙位置的优化同样重要。

大多数针对周期结构带隙特性优化的研究仍处于理论及仿真研究阶段，少数通过实验进行了对比验证。大多数结构在从理论研究转化为实际应用时仍存在不少问题，许多结构设计虽然理论上能够起到很好的振动衰减效果，但结构本身对制造精度、材料选取以及配比等有着极高的要求，现有的常用制作工艺难以满足，导致其减振效果受到极大影响甚至无法应用。在优化算法方面，虽然现有的优化算法足够成熟，可以实现各种目标的优化，但仍然存在计算效率较低的问题，如何通过对带隙机理的探究，明确与带隙相关的主要参数以简化优化过程，提升优化效率仍是今后需要探索的方向。此外，有效的运用机器学习、深度学习和人工神经网络等新颖的数据驱动模型，精准设计优化周期结构带隙特性，将会有利推动该研究领域的进一步发展。

整体来说，在过去的研究中，周期结构带隙特性优化已取得了很多研究成果，展现了其在提升结构减振隔振特性方面的巨大优势，有着很好的应用前景。在未来的研究工作中，应加强与实际工程应用的结合，以便在科技创新与新兴技术领域发挥其特长与优势。