Helmholtz声学超材料带隙特性分析
2022-10-09钟可欣孙维鹏赵道利刘园园马薇谭婷
钟可欣, 孙维鹏, 赵道利, 刘园园, 马薇, 谭婷
(1.西安理工大学 水利水电学院,陕西 西安 710048; 2.上海交通大学 机械与动力工程学院, 上海 200240)
声学超材料(acoustic metamaterials,AMs)是具有亚波长周期性的人工结构材料[1]。弹性波在声学材料中传播时,受内部结构的影响,存在一种特殊的色散关系,为人为调控弹性波提供了可能[2]。
振动带来的影响不容忽视[3],声学超材料的出现,为减振降噪等问题的解决提供了新思路[4]。Li等[5]设计了一种具有复合周期棒芯的新型弹性夹层超材料板, 利用有限元和谱元混合方法(FE-SEHM)计算了其动刚度矩阵,通过数值模拟和实验验证了其频率响应曲线。Jin等[6]提出了一种由层状蜂窝元结构组成的隔振器,基于布拉格散射和局部共振带隙对工程结构的噪声和振动问题进行了研究。Gao等[7]提出了一种具有2个谐振器的二维声子晶体,研究了其带隙特性。Oudich等[8]提出了一种具有复合散射体结构的声子晶体。Wang等[9]采用有限元方法研究了具有开口和闭口谐振腔的声子晶体板。Guenneau等[10]设计了一种具有双“C”谐振器的二维圆柱结构,该结构在低频下有很好的负折射效果。Popa等[11]提出了一种具有主动声学超材料的体系结构,其具有的负折射率、负有效质量密度和显著的非均匀性的特性可用于设计负折射率介质和具有可调增益和吸收特性。Gardezi等[12]数值模拟了由2个叠层钢板中互相连通的空腔组成的声学超材料的扭转行为。Mei等[13]提出了一种薄膜声学超材料,选择性完全吸收100~1 000 Hz内的低频声音。Jiang等[14]设计并实现了一种超宽带超材料的吸声材料。Li等[15]提出了一种散射体为双面阶梯谐振器的超材料,通过数值分析和实验验证了低频宽带弹性波的衰减和振动抑制。
近年来,具有Helmholtz谐振腔的声学超材料成为学者们的研究热点之一。Helmholtz谐振器是最基本的声学模型之一,在吸声降噪等领域被广泛应用。典型的Helmholtz谐振器由一个颈部和一个空腔组成。Fang等[16]设计了一种由刚性壁腔和一侧开一个小孔组成的Helmholtz谐振器,在共振频率附近具有负值的有效动模量,所研究的频率范围在20~50 kHz,该结构可用于负折射和超透镜领域。Han等[17]提出了一种具有刚性壁的新型Helmholtz型声子晶体,该结构由矩形腔体和“W”型空气通道组成,当晶格常数为62 mm时,第一完全带隙最小为12 Hz,带宽为14.6 Hz。Zhang等[18]设计了一种由腔体、连接颈部、顶部金属膜和穿孔板组成的Helmholtz谐振器(HHRs),采用数值模拟的方法对声辐射性能进行了研究。Li等[19]研究了Helmholtz谐振器嵌入流体基质的二维(平行的刚性狭缝管)/三维(刚性球型)声子晶体的声传输特性。Hu等[20]提出了一种由二维Helmholtz谐振器阵列组成的声子晶体,该晶体组成的声透镜具有较好的聚焦效果。Hu等[21]推导出流体中二维和三维Helmholtz谐振器声学超材料的有效质量密度和有效体积模量的解析式。Liu等[22]提出了一种由周期排列的耦合Helmholtz谐振器组成的宽带声能收集器,所提出的结构可以在频率范围为460~680 Hz下获得较高的输出电压。
以往对于Helmholtz谐振腔声学超材料的研究,其带隙范围主要集中在500 Hz以下或者大于10 kHz,完全带隙范围在1 000~5 000 Hz的研究相对较少,因此在本文研究的完全带隙范围选择在该范围内。提出了一种由Helmholtz谐振腔构成的新型声学超材料,采用有限元方法对其能带结构及其传输谱进行计算,并结合振动模态分析局域共振带隙的产生机理。其次,通过对Helmholtz谐振腔的结构参数进行设计,实现对弹性波的调控,最大可将完全带隙带宽拓宽至316.1 Hz,频率范围主要在1 000~4 000 Hz,所提出的结构对Helmholtz声学超材料的设计与研究提供理论指导。
1 模型及计算方法
1.1 有限元模型
提出了一种由Helmholtz谐振腔和铝板组成的声学超材料,如图1所示,图1(a)为该超材料的三维单元结构图、图1(b)为xoz平面上的剖面图、图1(c)为该单元组成的6×6有限周期超胞结构、图1(c)为布里渊区。单元结构的晶格常数为a=10 mm,基体厚度为t=0.4 mm,Helmholtz谐振腔内颈高度为h、半径为r1、内腔高度为h、半径为r2,Helmholtz谐振腔体厚度为s。如表1为本文在计算中使用的材料参数。

表1 材料参数Table1 Material parameter
1.2 能带结构计算方法
对于图1所提出的声学超材料,其能带结构可以基于基尔霍夫薄板理论作为控制方程来求解,其控制方程为[23]:
(1)
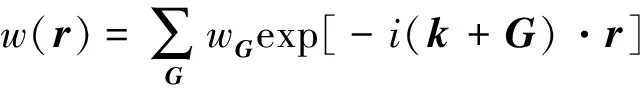
fj为谐振器施加在位置rj+R上的荷载,存在:
fj(rj+R)=fj(rj)exp(-ik·R)
(2)
(3)
式中S为单胞的面积。由于弹簧振子是基于单胞的力学近似,故有:
fj(rj)=-Kj(uj-w(rj))=-ω2mjuj
(4)
式中uj、Kj和mj分别为弹簧振子在该位置的振动位移、弹性刚度和质量。
联合上述公式即可对声学超材料的能带结构进行计算,也即:
SD[(kx+Gx)2+(ky+Gy)2]2wG+
exp[i(k+G)·rj]=Sρhω2wG
(5)
-Kj{∑G′wG′exp[-i(k+G′)·rj]-uj}=ω2mjuj
(6)
2 带隙形成机理
为进一步说明所提出的Helmholtz声学超材料的带隙形成机理,使用有限元分析软件COMSOL Multiphysics对特定的单元结构的能带结构及传输谱进行计算。选取结构参数r1=2.5 mm,r2=3 mm,h=4.5 mm,s=1.4 mm的Helmholtz声学超材料进行计算,其传输谱计算公式为[24]:
(7)
式中:out(solid.disp)为给定的位移激励;in(solid.disp)为输出的位移响应。本文考虑在x方向上存在10个单元结构组成的有限阵列,在y方向上仍应用周期性边界条件来表示无限个单元结构,在阵列结构的一端沿z方向给出一个位移激励,得出位移响应即可获得该结构的传输谱。
如图2为选定的Helmholtz声学超材料的能带结构图和传输谱,图中阴影部分(2 449.3~2 758.4 Hz)为该结构的完全带隙,而方向带隙的频率范围为2 269.8~2 449.3 Hz和2 758.4~3 143.2 Hz,从图中可以看出,完全带隙、方向带隙和传输谱的频率范围基本吻合,在完全带隙和方向带隙的频率范围内,输出的位移激励小于输入的位移激励,弹性波在传播过程中受到了衰减,也即在完全带隙频率范围内可以很好地抑制弹性波。在完全带隙的频率范围内,出现了2条平直带,即2 629.8 Hz和2 632 Hz。
如图3(a)~(e)为图2能带结构图中点a~f的振动模式,a点位于完全带隙的起始频率上,其振动模式为Helmholtz谐振腔的扭转模式,而基板保持静止状态,也即弹性波主要作用在Helmholtz谐振腔上。b点和c点是禁带中的本征模,不同波矢几乎对应于相同的本征频率,从而导致平直带的出现,根据声学超材料的局域共振机制,禁带的出现不仅取决于局域本征模和共振“平带”,还取决于共振带与基板Lamb模之间的模式耦合[15]。b点和c点在z方向振动几乎为0,没有和基板的Lamb模耦合,也即未对低频带隙造成影响。d点位于完全带隙的截止频率上,其Helmholtz谐振腔处于扭转模式,而基板在z方向存在很小的振动。e点的振动模式为基板沿着z方向向上运动,内颈沿着z方向向下运动。f点在带隙的下边界,对应于带隙的固有频率,其振动模式为沿着z方向垂直运动。
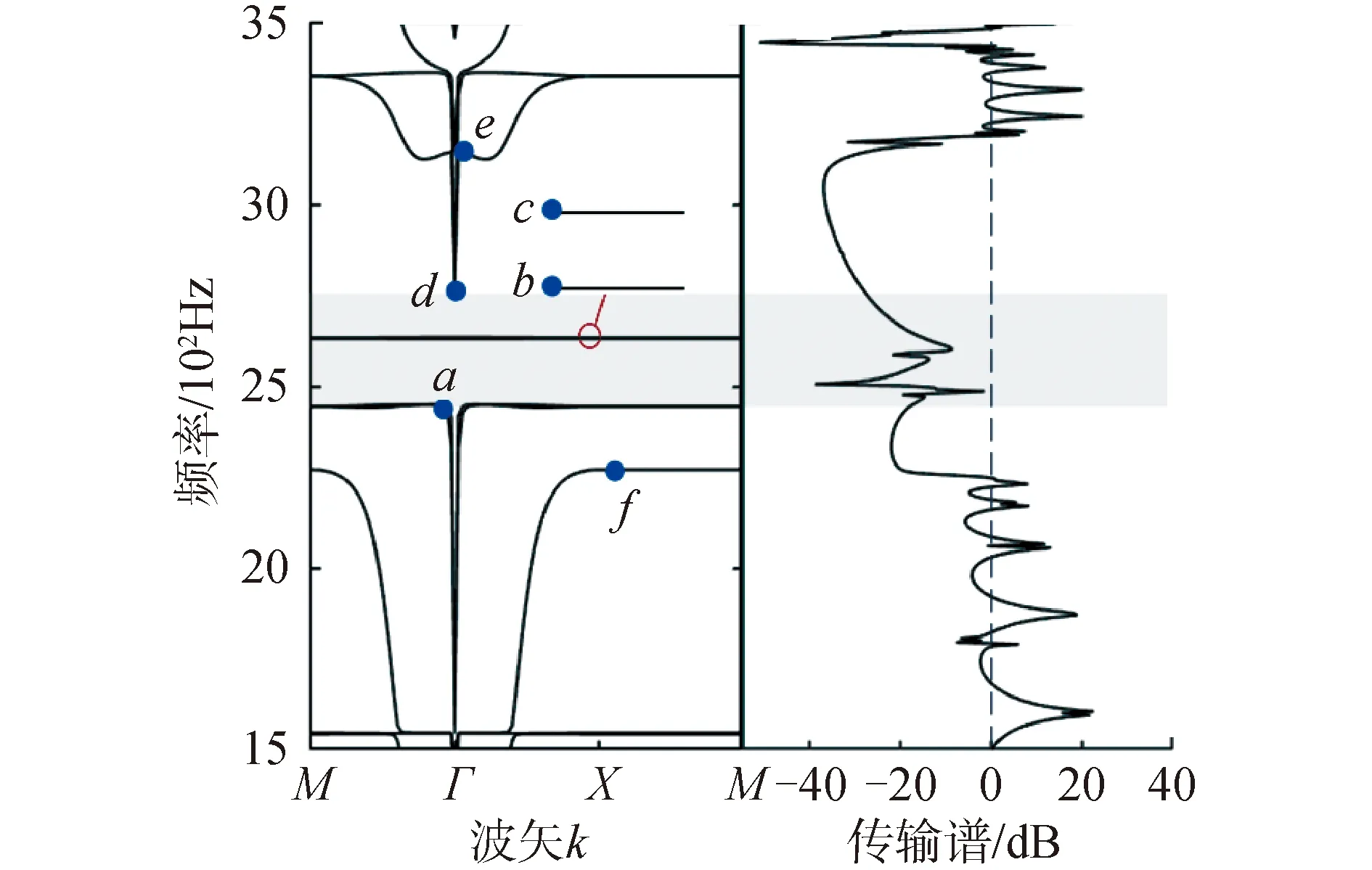
图2 能带结构及传输谱Fig.2 Band structure and transmission spectrum
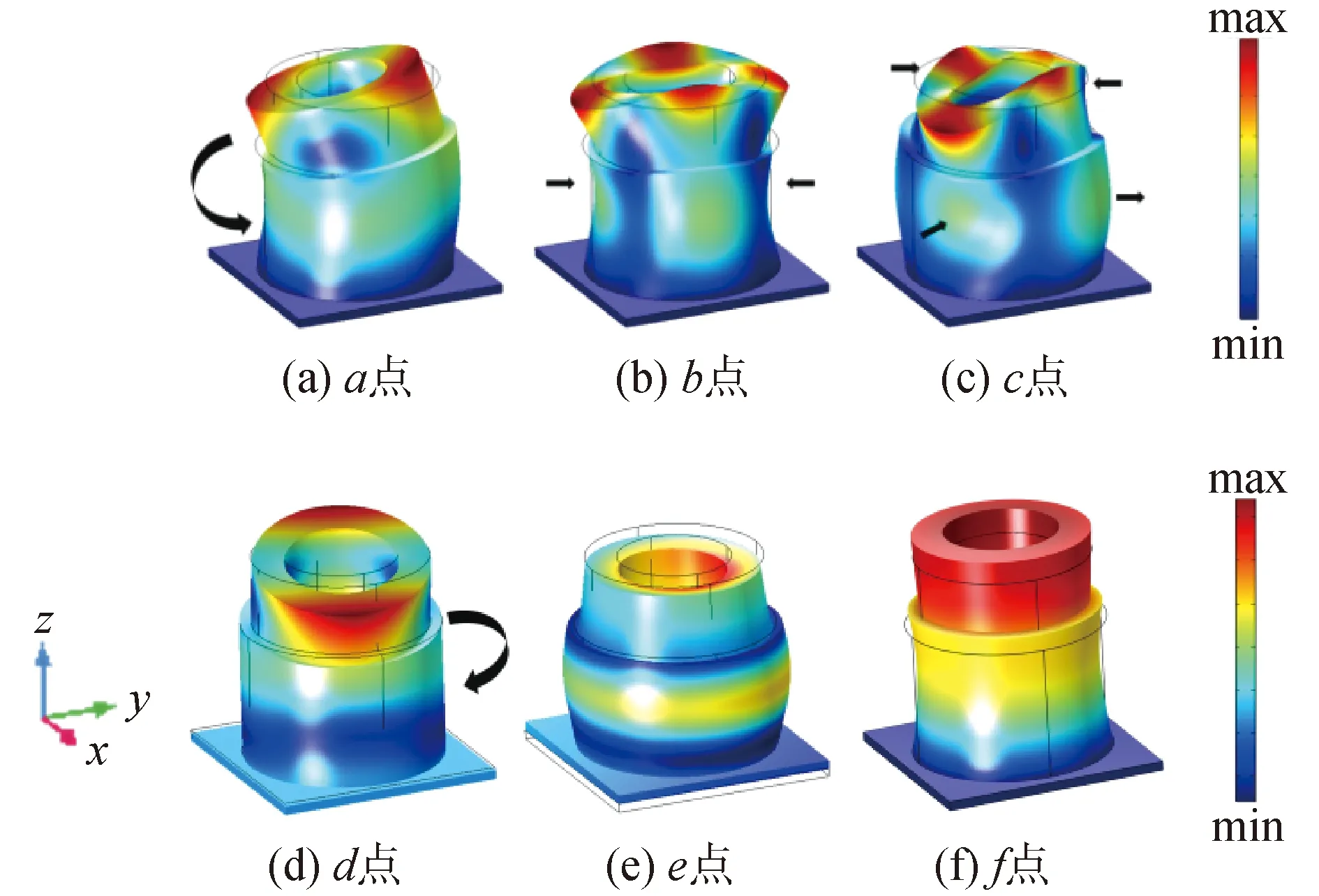
图3 振动模式Fig.3 Mode of vibration
3 完全带隙影响因素分析
局域共振单元可以等效为“质量-弹簧”系统,带隙的起始频率(固有频率)与谐振器的等效刚度和等效质量有关;而计算带隙的截止频率时,局域共振单元等效为“质量-弹簧-质量”系统,与等效刚度和散射体与基板质量有关[25]。故在分析结构参数对超材料能带结构的影响时,分别研究Helmholtz谐振腔内颈半径r1、内腔半径r2、内颈(内腔)高度h等结构参数对完全带隙的起始频率、截止频率和带宽的影响。
如图4所示,当h=4 mm,s=1 mm时,图4(a)~(c)分别为当控制r1为3.5 mm、3 mm和2.5 mm时,完全带隙起始频率和截止频率随内腔半径r2的变化曲线图,图4(d)为带宽随r1、r2的变化曲线图。从图2(a)~(c)可以看出,当改变r1的值从1~3 mm、改变r2的值为2.5~3.5 mm时,Helmholtz声学超材料的完全带隙起始频率和截止频率均在2 000~3 000Hz内。当r2不变时,完全带隙的起始频率和截止频率随着r1的增大而增大;当r1不变时,完全带隙的起始频率和截止频率随着r2的增大而减小。由此可得,Helmholtz声学超材料的起始频率和截止频率与内颈半径r1呈正相关,与内腔半径r2呈负相关。从图4(d)可得,Helmholtz声学超材料带宽随着内径r1的增大而增大,随着内腔半径r2的增大而减小,当r1=2 mm,r2=2.5 mm时,带宽最大值为226.5 Hz。由此可得,当内颈半径r1不变时,减小内腔半径r2可以获取更宽的带隙;当内腔半径r2不变时,增加内颈半径r1可以获取更宽的带隙,但增加内颈半径r1或减小内腔半径r2时,完全带隙的起始频率和截止频率均会增加。
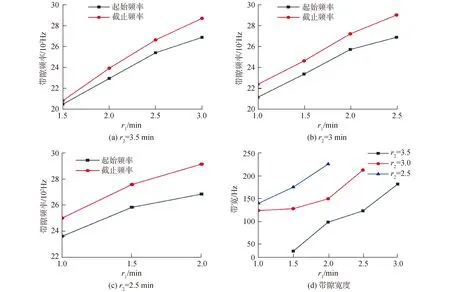
图4 r1、r2对完全带隙的影响Fig.4 Effect ofr1 andr2 on absolute band gap
图5为当r1=2.5,r2=3,s=1时,研究改变内颈、内腔高度h对完全带隙起始频率、截止频率和带宽的影响。由图5可得,Helmholtz声学超材料的完全带隙起始频率和截止频率随着h的增大而减小,起始频率由3 665.9 Hz减小到1 497.8 Hz,截止频率由3 709 Hz减小到1 674.1 Hz,而带宽随着h的增大而增大,当增大到5.5 mm时达到最大值(265.6 Hz),接着随着h的增大而减小,由此可见,内颈和内腔h与完全带隙的带宽并不呈正相关,但和完全带隙的起始和截止频率呈负相关,在进行结构设计时,选取最优的h值不仅可以节省材料,还能获得更宽的带隙。
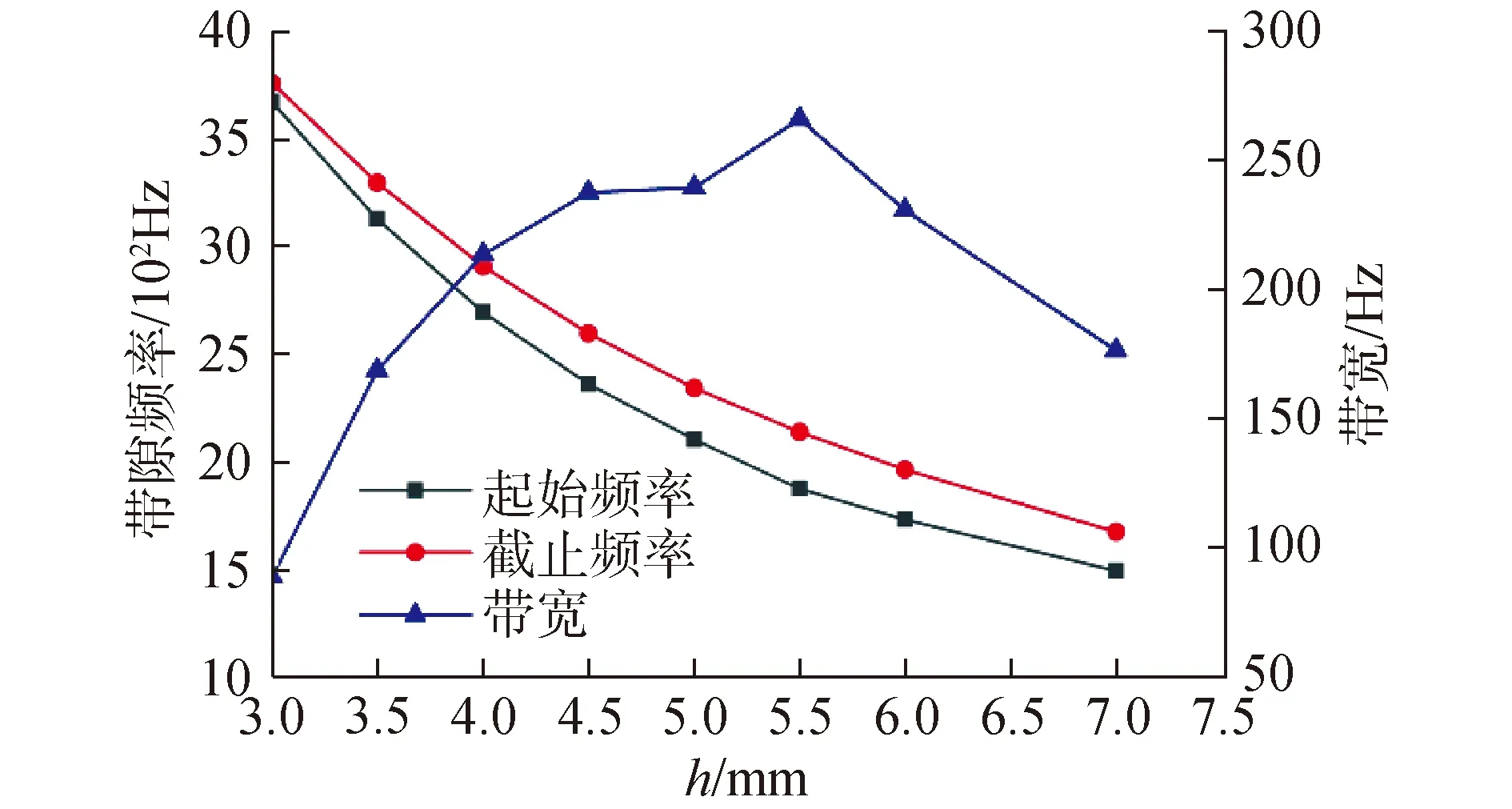
图5 h对完全带隙的影响Fig.5 Effect ofh on absolute band gap
固定r1=2.5 mm、r2=3 mm,研究腔体厚度s对能带结构的影响时分为2个方案,首先是保持Helmholtz谐振腔腔体大小不变,向两端增加s值(0.4~1.4 mm),如图6(a),研究其对能带的影响;接着保持r1+s和r2+s的值不变,改变腔体大小,也即向内增加s的值,如图6(b),研究其对能带的影响。
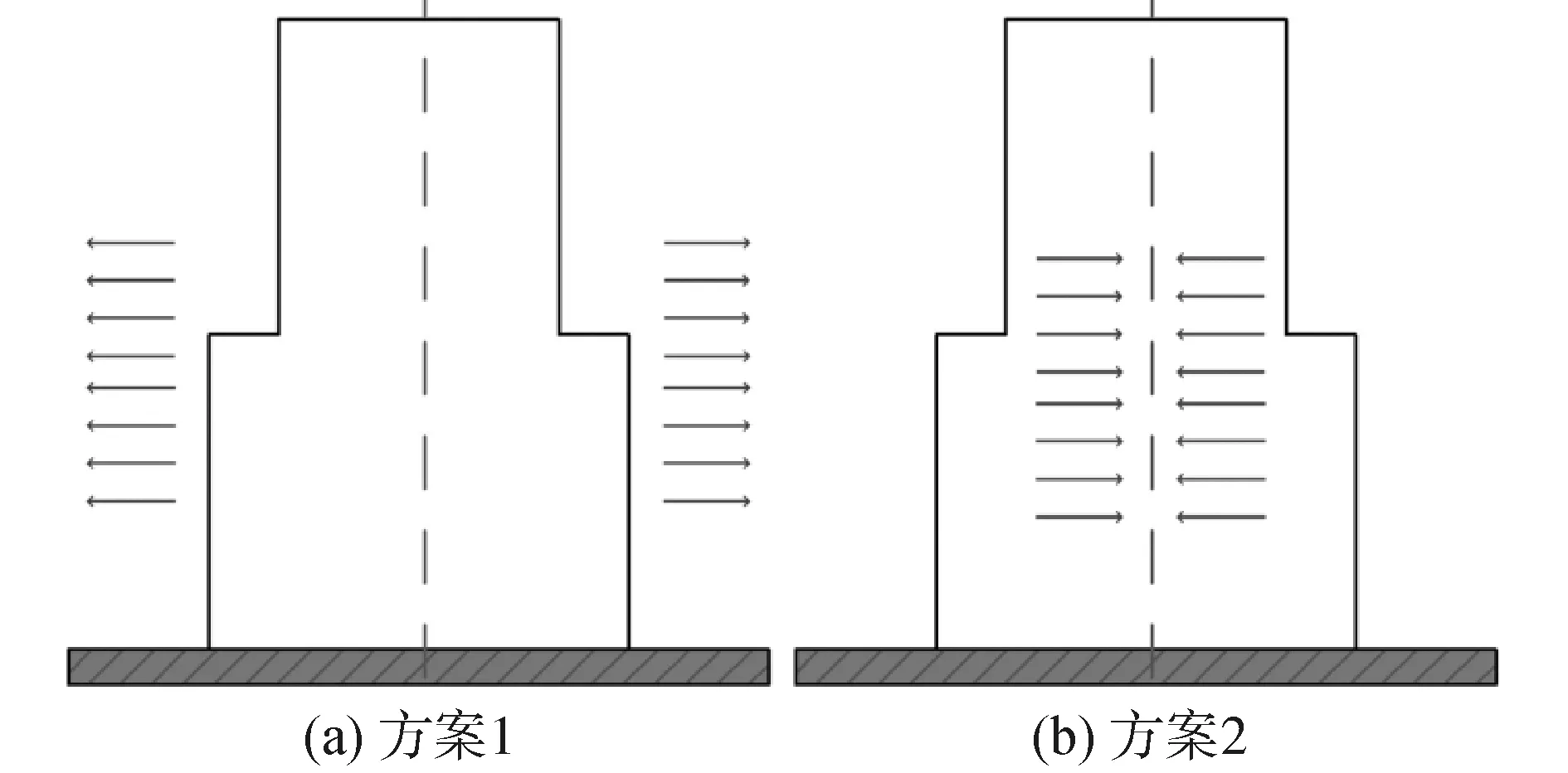
图6 不同方案对比Fig.6 Comparison chart of different solutions
如图7为方案1和方案2中s对完全带隙的影响。从图7(a)可知,当保持Helmholtz谐振腔的空气腔体大小不变时,随着腔体厚度s增大,Helmholtz声学超材料的完全带隙起始频率和截止频率增大,起始频率从2 055 Hz增大到2 481.4 Hz,截止频率从2 155.3 Hz增大到2 815.6 Hz,起始频率增大的速率小于截止频率,故而随着s增大,带宽也逐渐增大,当s增大到1.4 mm时,带宽最大值为334.2 Hz。从图7(b)可知,改变Helmholtz谐振腔的空气腔体大小,也即随着s的增大,Helmholtz谐振腔的空气腔体减小,Helmholtz声学超材料的带隙起始频率和截止频率增大,其带宽也随之增大,起始频率从2 071.2 Hz增大到2 403 Hz,截止频率从2 094.8 Hz增大到2 633 Hz,当s增大到1.4 mm时,带宽最大值为230 Hz。由此可得,随着s的增大,方案1和方案2的完全带隙起始频率增加速率差不多,但方案2的完全带隙截止频率的增加速率小于方案1的截止频率,因此方案1的带宽增长速率大于方案2的增长速率。所以在Helmholtz谐振器的结构设计中,在消耗相同的材料的情况下,选择方案1可以获得更宽的带隙范围。
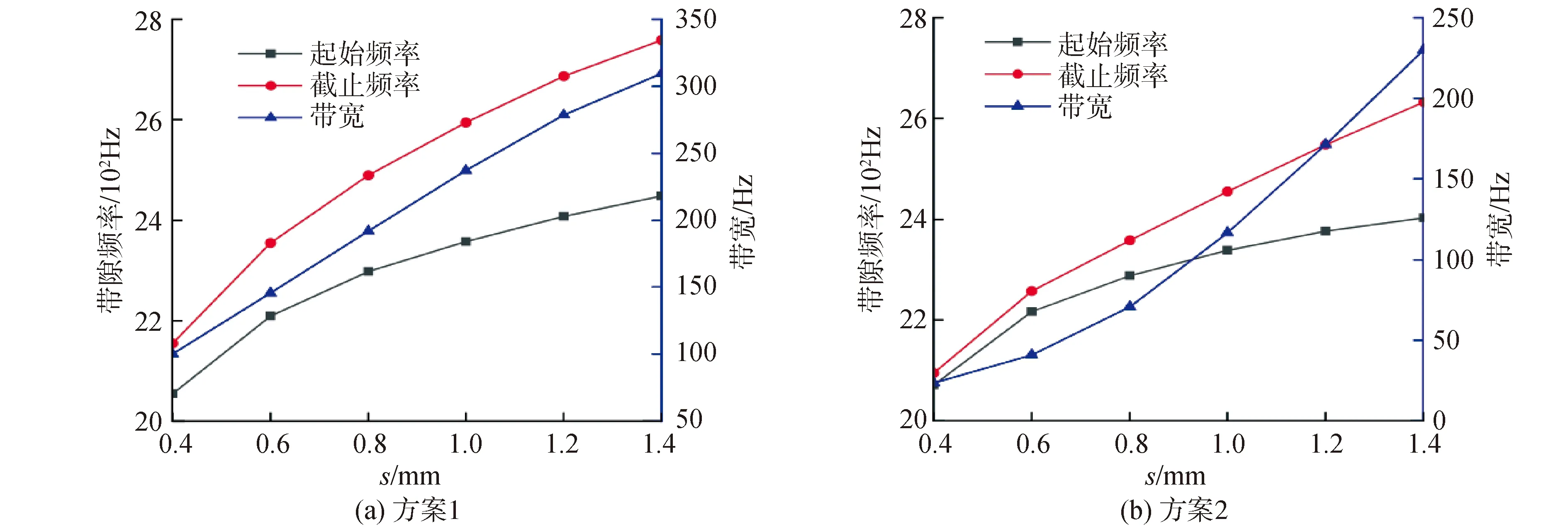
图7 腔体厚度s对完全带隙的影响Fig.7 Effect ofs on absolute band gap
4 结论
1)单元结构的完全带隙的起始频率和截止频率与内颈半径和腔体厚度呈正相关,与内腔半径和腔体高度呈负相关;
2)单元结构的完全带隙频率范围与内颈半径和腔体厚度呈正相关,与内腔半径呈负相关,而随着腔体高度的增加,带隙逐渐增大,在最佳高度时带隙宽度达到最大值。因此,在对超材料进行设计时,合理的选择单元结构的结构参数可以调控其在不同频率范围下对弹性波的抑制。
