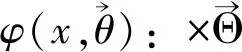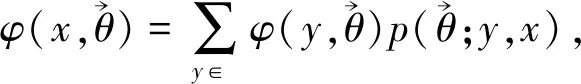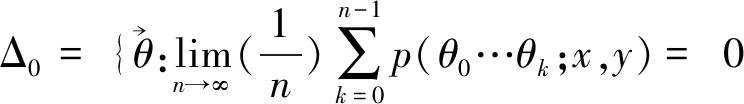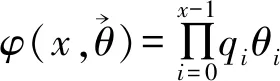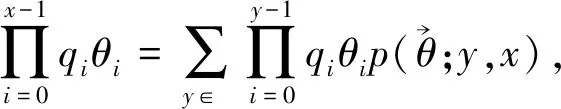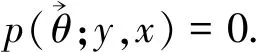依空随机环境中的更新过程
2022-10-08池夏夏
池夏夏,吕 平
(杭州师范大学数学学院,浙江 杭州 311121)
0 引言
20世纪80年代初, Cogburn[1-2]首次在马尔可夫链的影响因素中添入新的环境因素,并给出了随机环境中马尔可夫链随机模型的一般表达式,研究了其遍历理论以及有限不变测度存在的条件,使已有的经典马尔可夫链理论及其完整体系更加丰富. Hu[3-4]进一步对随机环境中马尔可夫过程进行推广和整理,形成目前完整随机环境中马尔可夫过程的理论体系,为后续了解并研究随机环境中的马尔可夫过程提供了理论依据. Li[5]研究了引入“初始时间”马尔可夫链的弱遍历性、一致弱遍历性、强遍历性和一致强遍历性等. Lü等[6]在给定条件下,给出了随机环境中某种扩散的重对数律. Hu[7]系统介绍了随机环境中的马尔可夫过程,为后续研究奠定了基础.本文在前人研究基础上,通过定义随机转移概率构建随机环境中的更新过程模型,给出其初达转移概率以及随机不变测度,进一步丰富了随机环境中的马尔可夫链理论.
1 符号及定义


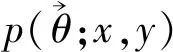
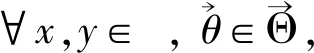
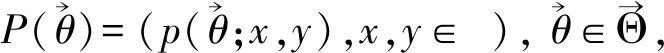

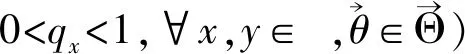
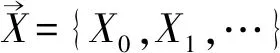

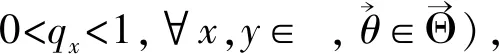
附注2规定qjθj≡1,当j=-1时,如不加以说明,该规定适用于全文.
Cogburn在文献[1-2]中分析了马尔可夫链与随机环境之间的关系,证明了随机环境中马尔可夫链的马氏性,探讨了其遍历理论,给出了有限不变测度存在的条件.最后讨论了状态分类以及连通性特性.本文研究依空随机环境中更新过程的马氏性、遍历理论以及随机不变测度的相关问题.下面给出依空随机环境中更新过程马氏性的直接结果.
定理1依空随机环境中的更新过程是随机环境中的马尔可夫链.
证明由依空随机环境中更新过程的定义以及Hu[7]对随机环境中马尔可夫链的定义易知,定理显然成立.
进一步研究依空随机环境中更新过程的遍历理论、不变测度,并得出其有关结论.
2 遍历理论
从随机环境中初达概率的定义出发,给出依空随机环境中更新过程初达概率的具体表达式,进而探究其遍历性质.


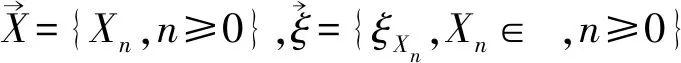
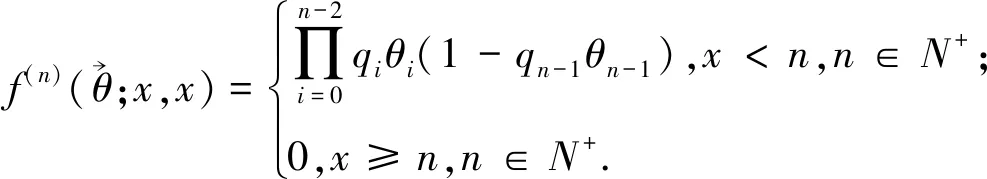
(1)
证明当x≥n时,式(1)显然成立. 故剩证x 首先考虑x=0, q0θ0q1θ1…qn-2θn-2(1-qn-1θn-1)= 其次考虑x≠0,此时有 qxθxqx+1θx+1…qn-2θn-2(1-qn-1θn-1)q0θ0…qx-1θx-1= 证毕. 为了进一步考虑依空随机环境中更新过程的遍历性,先探讨其在状态x=0处的常返性,了解关于状态可达以及状态互通的相关定义. 由依空随机环境中更新过程的随机转移概率的定义易知,各状态之间都是互通的. 而 因此该依空随机环境中的更新过程在状态x=0处具有常返性,显然它是非周期的.故此时0是遍历状态.对其他任意状态y∈X,由于y↔0.因而y也是遍历状态. 证明先考虑更新次数k=1的情况,此时更新间隔为m1.由已知随机转移概率可知, p(θ0;0,1)p(θ1;1,2)…p(θn-m1-1;n-m1-1,n-m1)= qxθx…qx+m1-2θx+m1-2(1-qx+m1-1θx+m1-1)q0θ0q1θ1…qn-m1-1θn-m1-1= 故k=1时,等式成立. 其次,当更新次数k≥2时,此时更新间隔分别为m1,m2,…,mk. qxθx…qx+m1-2θx+m1-2(1-qx+m1-1θx+m1-1)q0θ0…qm2-2θm2-2(1-qm2-1θm2-1)… 综上,证毕. 对不变测度进行研究,从随机不变测度的定义出发,得出依空随机环境中更新过程的随机不变测度. (2) 由文献[2]可知, Δ1表示的是所有满足φ(X×·)=π环境的集合. 证明先证不变测度的存在性. 本文已证明依空随机环境中的更新过程是马尔可夫链,再由文献[1]中定理3.1(2)可知,不变测度存在. (3) 其次考虑x=0的情况,此时 q-1θ-1(1-q0θ0)+q0θ0(1-q1θ1)+q0θ0q1θ1(1-q2θ2)+…= 1-q0θ0+q0θ0-q0θ0q1θ1+q0θ0q1θ1-q0θ0q1θ1q2θ2+…= 而 因此满足式(3). 最后考虑其他情况,即x≠0且x≠y+1.此时 要使 恒成立,当且仅当 综上所述,证毕.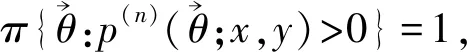
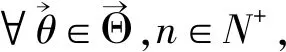


3 不变测度