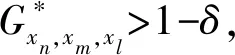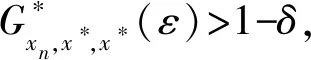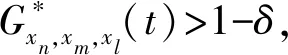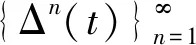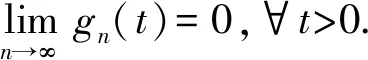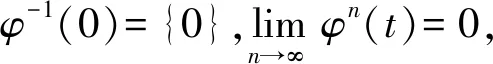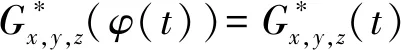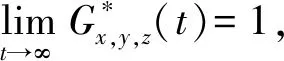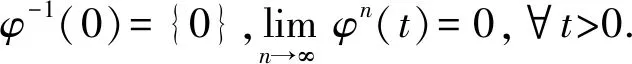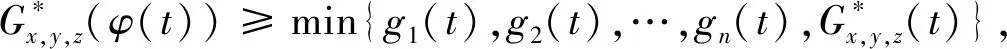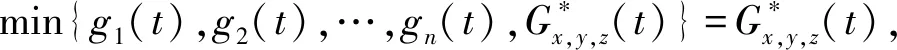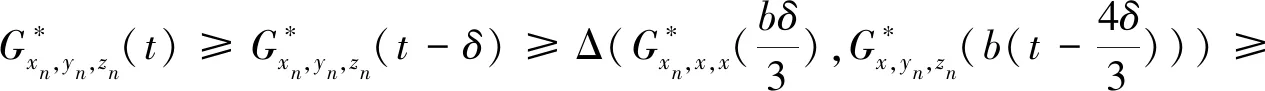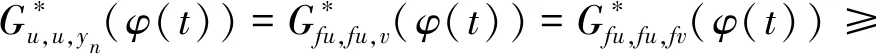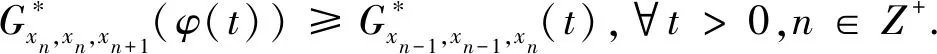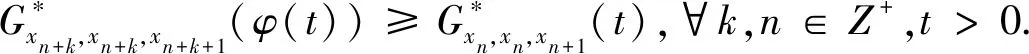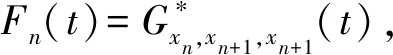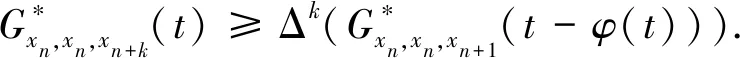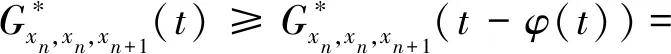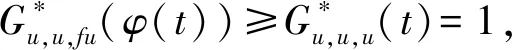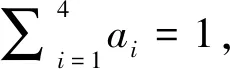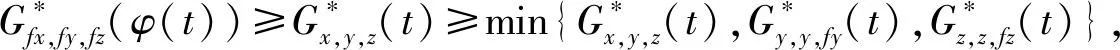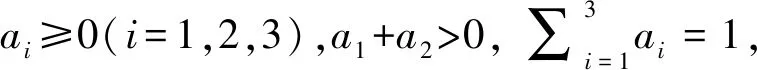Menger概率Gb-度量空间中的不动点问题研究
2022-10-08林亚磊
林亚磊,谷 峰
(杭州师范大学数学学院,浙江 杭州 311121)
1 引言和预备知识
自2019年Aghajani等[1]提出Gb-度量空间概念以来,Gb-度量空间中的相关理论得到了迅猛发展[2-5].本文在Gb-度量空间框架下,引入MengerPGbM-空间概念,证明该空间的拓扑性质和该空间中的一些不动点定理.
定义1[6]称映射F:R→R+为分布函数,如果它是单调不减的、左连续的,且满足inft∈RF(t)=0,supt∈RF(t)=1.
用D表示一切分布函数的集合,D+={F∈D:F(t)=0,∀t≤0},H(t)表示一特殊的分布函数,其定义如下:
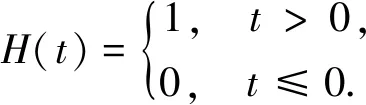
定义2[7]若映射Δ:[0,1]×[0,1]→[0,1],且∀a,b,c,d∈[0,1],有下列条件被满足:
(Δ-1) Δ(a,1)=a;
(Δ-2) Δ(a,b)=Δ(b,a);
(Δ-3)a≥c,b≥d⟹Δ(a,b)≥Δ(c,d);
(Δ-4) Δ(Δ(a,b),c)=Δ(a,Δ(b,c)).
则称Δ为三角范数(简称t-范数).
3个典型的t-范数是:
Δ1(a,b)=min{a+b-1,0},Δ2(a,b)=ab,Δm(a,b)=min{a,b},∀a,b∈[0,1].
以上3个t-范数显然满足:Δ1≤Δ2≤Δm.
定义3[8]MengerPM-度量空间是一个三元组(X,F,Δ),其中X是一个非空集合,Δ是一个连续的t-范数,F:X×X→D是满足下面条件的映射:
(PM-1)Fx,y(t)=1⟺x=y,∀x,y∈X,∀t>0;
(PM-2)Fx,y(t)=Fy,x(t),∀x,y∈X,∀t>0;
(PM-3)Fx,z(s+t)≥Δ(Fx,y(s),Fy,z(t)),∀x,y,z∈X,∀s,t>0.
定义4[9]设X是一个非空集合,G:X×X×X→R+为一函数,且满足以下条件:
1)G(x,y,z)=0⟺x=y=z;
2)G(x,x,y)>0,∀x,y∈X且x≠y;
3)G(x,x,y)≤G(x,y,z),∀x,y,z∈X且z≠y;
4)G(x,y,z)=G(x,z,y)=G(y,z,x)=…,∀x,y,z∈X;
5)G(x,y,z)≤G(x,a,a)+G(a,y,z),∀x,y,z,a∈X.
则称函数G是X上的一个广义度量,简称为X上的一个G-度量,并称(X,G)是一个广义度量空间,简称为G-度量空间.
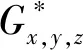
定义6[11]设X是一个非空集合,给定一个常数b≥1,使得函数
Gb:X×X×X→[0,+∞)
满足:
(Gb1)Gb(x,y,z)=0⟺x=y=z,∀x,y,z∈X;
(Gb2) 0 (Gb3)Gb(x,x,y)≤Gb(x,y,z),∀x,y,z∈X且y≠x; (Gb4)Gb(x,y,z)=Gb(x,z,y)=Gb(y,z,x)=…,∀x,y,z∈X; (Gb5)Gb(x,y,z)≤b(Gb(x,a,a)+Gb(a,y,z)),∀x,y,z,a∈X. 则称函数Gb是X上的一个广义b-度量,简称为X上的一个Gb-度量,并称(X,Gb)是一个广义b-度量空间,简称为Gb-度量空间. 综合上述定义,本文引入MengerPGbM-空间的概念如下: 注1由定义易知,当b=1时,MengerPGbM-空间就是一个MengerPGM-空间.但当b>1时,MengerPGbM-空间显然不是MengerPGM-空间. 定义8设(X,G*,Δ)是一个MengerPGbM-空间,x0∈X,对于任意的ε>0和0<δ<1,定义x0的(ε,δ)-邻域如下: 引理 1若0<ε1≤ε2,0<δ1≤δ2<1,则Nx0(ε1,δ1)⊂Nx0(ε2,δ2). 因此,由定义8得到z∈Nx0(ε2,δ2),故Nx0(ε1,δ1)⊂Nx0(ε2,δ2). 定理1设(X,G*,Δ)是一个MengerPGbM-空间,则(X,G*,Δ)是一个Hausdorff空间(在(ε,δ)-邻域族{Nx0(ε,δ):x0∈X,ε>0,0<δ<1}诱导的拓扑下). 即MengerPGbM-空间(X,G*,Δ)具有下列性质: 1)任取x0∈X,则至少存在x0的一个邻域Nx0,并且x0的任何一个领域都包含x0; 3)若Nx0是x0的邻域,且y0∈Nx0,则存在y0的邻域Ny0,使得Ny0∈Nx0; 4)若x0≠y0,则存在x0的邻域Nx0和y0的邻域Ny0,使得x0∈Nx0,y0∈Ny0,且Nx0∩Ny0=∅. 2)对于任意的ε1,ε2>0和0<δ1,δ2<1,令 是x0的两个邻域,取ε3=min{ε1,ε2},δ3=min{δ1,δ2}.令 因为Δ是连续的,且Δ(1-δ0,1)=1-δ0>1-δ1,所以存在δ2∈[0,1],使得Δ(1-δ0,1-δ2)>1-δ1. Δ(1-δ0,1-δ2)>1-δ1. 下证Nx0∩Ny=∅.否则,如果存在u∈Nx0∩Ny,则 使用(PGbM-4),得 这显然矛盾,故Nx0∩Ny=∅. 定义9设(X,G*,Δ)是一个MengerPGbM-空间,{xn}是X中的序列,x*∈X. 3)若X中的所有柯西序列都在X中收敛,则称(X,G*,Δ)是完备的. 引理2设(X,G*,Δ)是一个MengerPGbM-空间,{xn}是X中的序列,则以下叙述等价: 1){xn}收敛于x*∈X; 2)⟹3).因为 3)⟹2).因为 引理3设(X,G*,Δ)是一个具有连续t-范数Δ的MengerPGbM-空间,则以下叙述等价: 1)序列{xn}是柯西序列; 2)⟹3)显然成立. 3)⟹2).因为 为证主要结果,需要以下概念和引理. 显然有Δm(t)≤t,∀m∈Z+,t>0. 一个典型的H型t-范数是:Δm=min{a,b},其中a,b∈[0,1]. 定义11[13]如果函数φ:R+→R+满足φ(0)=0,则称φ是一个度规函数.如果t∈R+,则φn(t)表示φ(t)的n次迭代,φ-1(0)={t∈R+:φ(t)=0}. (1) 引理7设(X,G*,Δ)是一个具有连续t-范数Δ的PGbM-空间,xn,yn,zn是X中的3个序列,x,y,z∈X.如果{xn}→x,{yn}→y,{zn}→z(n→∞),则对任意t>0,有 证明对于任意的t>0,存在δ>0,使得t>2δ,由(PGbM-4)可得 和 如果∀x,y,z∈X,t>0,映射f:X→X满足下列条件: (2) 则映射f在X中有唯一的不动点. 证明任意x0∈X,定义迭代序列{xn}为xn=fxn-1,n∈Z+. 由式(2)可知,对于任意的t>0,有 由引理6得到,对于任意的t>0,有 (3) (4) 下证对于任意的k∈Z+,t>0,有 (5) 使用数学归纳法.当k=1时,有 即当k=1时,式(5)成立.假设当k=p时,式(5)成立,即 (6) 则当k=p+1时,由(PGbM-4)可得 (7) 由φ(t) 重复使用上式可得 (8) 由式(2),(8)和(6)可得 (9) 由式(7),(9)可得 上式说明,当k=p+1时,式(5)成立.由数学归纳法知,式(5)对于任意t>0,n,k∈Z+成立. 下证{xn}是一个柯西列. 下证fu=u.事实上,∀t>0,由φ(t) 最后证明不动点的唯一性. 设v∈X是f的另一个不动点,定义序列{yn}:yn=v,n∈Z+.则由式(2),∀t>0有 Qn(φn(t))≥Qn-1(φn-1(t))≥…≥Q1(φ(t))≥Q0(t). (10) 证明任取x0∈X,定义xn=fxn-1,∀n∈Z+,则{xn}是一个柯西列.由式(10),φ(t) (11) 反复利用上式,并注意到φ(t) 即 (12) (13) 下证,对于任意的k∈Z+,t>0,有 (14) 当k=1时,由G*的不减性和Δ的性质,有 即当k=1时,式(14)成立.假设当k=p时,式(14)成立,即有 (15) 则当k=p+1时,由式(10),(12),(15)和G*的不减性可得 使用(PGbM-4)和式(16)可得 即k=p+1时,式(14)也成立.由数学归纳法知,式(14)对于任意的k∈Z+,t>0都成立.同定理2相应部分的证明,可得{xn}是X中的柯西列.由X的完备性可知,存在u∈X,使得xn→u(n→∞). 下证fu=u.事实上,由式(10)及G*的不减性,有 在上式中令n→∞,使用引理2和引理7可得 最后证明u是f的唯一不动点.事实上,假设v∈X是f的另一个不动点,即fv=v,则由式(10)有 下面给出几个推论. 在定理2中令φ(t)=λt,λ∈(0,1),则可得推论1. 推论1设(X,G*,Δ)是一个完备的MengerPGbM-空间,其中Δ是H型t-范数,λ∈(0,1).如果f:X→X满足下列条件: ∀x,y,z∈X,t>0.则f在X中有唯一的不动点. ∀x,y,z∈X,t>0.则f在X中有唯一的不动点. 对于任意的x,y,z∈X,t>0.则f在X中有唯一的不动点. 在定理3中令a1=0,则可得以下推论4.
2 Menger PGbM-空间的拓扑性质
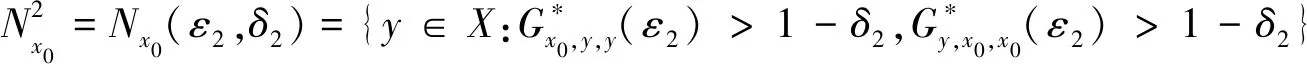
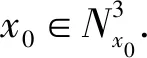

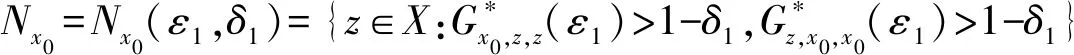
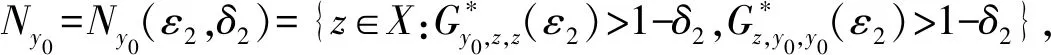
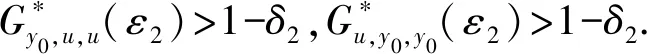
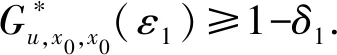

3 Menger PGbM-空间中的不动点定理