一阶非线性中立型脉冲微分方程解的振动性
2022-10-08韦晶晶申建华
韦晶晶, 申建华
(杭州师范大学数学学院,浙江 杭州 311121)
0 前言
众所周知,脉冲微分方程是研究动力学过程中状态突然发生变化的基本模型.在过去的几十年中,脉冲微分方程已被广泛研究.关于时滞微分方程和中立型时滞微分方程解性质的研究工作已十分丰富[1-9].文献[10-18]研究了脉冲扰动下时滞微分方程解的振动性.
文献[12]考虑了系统
(1)
得到了关于系统(1)所有解振动的充分条件.
文献[14]在文献[12]的基础上,研究了如下一阶中立型时滞微分方程
(x(t)-p(t)x(t-τ))′+q(t)G(x(t-σ))=0,t≠tk,t≥t0
(2)
本文的目的是研究如下中立型脉冲微分方程
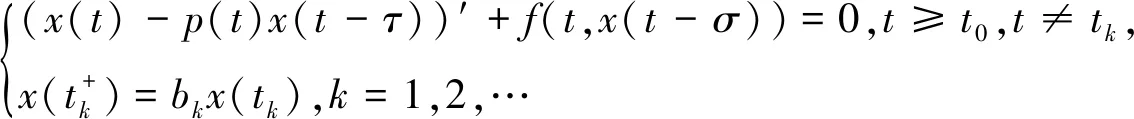
(3)
解的振动性,其中假设后面的条件(A)成立.为此先给出有关定义与假设.
定义1设I,J⊂,称函数φ:I→J属于PC(I,J),如果满足:

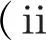
定义2实值函数x(t)被称作是系统(3)的解,如果满足:


系统(3)的解如果最终为正或者最终为负,则称解是非振动的.否则就称系统(3)的解为振动的.
假设如下条件(A)成立:
(A1)对t≥t0,f(t,u)关于u∈是奇函数,即f(t,-u)=-f(t,u);
(A2)存在g(t)≥0,G(u)>0, 使得f(t,u)≥g(t)G(u)对任意u>0和t≥t0成立;
(A3)τ∈(0,∞),σ∈(0,∞),p(t)∈PC([t0,∞),+),其中+=[0,∞). {tk} 是一个严格单调增加的正实数序列,满足0≤t0 (A4)G是非增的,对u≠0,有uG(u)>0.那么,存在一个常数L>0,使得|G(u)|≥L|u|,u∈.事实上,G可以写成G(u)=u(L+|u|μ),u∈,μ>0. 本节将给出一些引理,并运用这些引理得出系统所有解振动的充分条件.其中引理2的证明思想参考文献[12],但是文献[12]在对l个脉冲点进行排列后,并未考虑左端点t是否为脉冲点,这对于接下来证明过程中z(t)的单调性是否适用起着关键性的作用.本文对t是否为脉冲点的两种情况加以讨论,相较文献[12]更加严谨. 引理1假设条件(A)满足,存在一个序列{sn},使得对任意的n=1,2,…,有sn∈(tn,tn+1],sn+1-sn=τ,p(sn)>0,且 (4) 进一步,假设 (5) (6) z(t)=x(t)-p(t)x(t-τ), (7) 证明由(A4)和(7),有 z′(t)=-f(t,x(t-σ)≤-g(t)G(x(1-σ))≤-Lg(t)x(t-σ),tk (8) 首先有z(tk)≥0,k≥1.否则一定存在某个m≥1,使得z(tm)<0.由式(7),有 对k∈K1k,根据式(5)有 对k∈K2k,根据式(6)有 bkx(tk)-bkp(tk)x(tk-τ)=bkz(tk). 因为K1k∪K2k={1,2,…},由此可得 (9) 通过归纳,不难得到 从而,当n=1,2,…,式(7)意味着 x(sm+n)=z(sm+n)+p(sm+n)x(sm+n-1)≤ -bmbm+1…bm+nμ+p(sm+n)x(sm+n-1)≤ -bmbm+1…bm+nμ-p(sm+n)bmbm+1…bm+n-1μp(sm+n)p(sm+n-1)bmbm+1…bm+n-2μ-…- p(sm+n)p(sm+n-1)…p(sm+2)bmbm+1μ-p(sm+n)p(sm+n-1)…p(sm+2)p(sm+1)x(sm)= 这与事实z(tm+1)>0矛盾.从而,对t∈(tk,tk+1],k=0,1,2,…,有z(t)≥z(tk+1)>0.因此,z(t)>0 对任意t≥t0成立.引理证毕. 引理2引理1中所有假设都满足.此外,假设存在p∈(0,1],b>0,a>0,使得 p(t)≥p,bk≤b,tk+1-tk≥α,k=1,2,…. (10) 假设系统(3)有一解x(t),且x(t-σ)>0,t≥t0.令T=max{t0+σ,t0+τ},m=min{k:tk>T}.那么二阶脉冲微分不等式 (11) t 由式(8)和(9)有 如果t不是脉冲点,即t≠ti-1,那么 z(t)(ti-t)+biz(ti)(ti+1-ti)+…+bi…bi+lz(ti)(t+τ-ti+l)≤ z(t)(ti-t)+biz(t)(ti+1-ti)+…+bi…bi+lz(t)(t+τ-ti+l)≤ z(t)(ti-t)+bz(t)(ti+1-ti)+…+bl+1z(t)(t+τ-ti+l)≤ 如果t是脉冲点,即t=ti-1,那么一定有t≥t1,也就是i-1≥1.又bk≤b,对k=1,2,…成立,从而可知bi-1≤b.此时, bi-1z(ti-1)(ti-t)+biz(ti)(ti+1-ti)+…+bi+lz(ti+l)(t+τ-ti+l)≤ bi-1z(ti-1)(ti-t)+bi-1biz(ti-1)(ti+1-ti)+…+bi-1…bi+lz(ti-1)(t+τ-ti+l)≤ bz(t)(ti-t)+b2z(t)(ti+1-ti)+…+bl+2z(t)(t+τ-ti+l)≤ 令M=min{x(t):t0-τ≤t≤t0},对t∈(t0,t0+τ],有 对t∈(t0+τ,t0+2τ],有 通过归纳,对于t∈(t0+nτ,t0+(n+1)τ],有 因此,对于t∈(t0,∞),有 (12) 下面,分两种情况讨论. 情况Ⅰσ>τ. 对t>t0+σ,有 又t0≥0,上面的不等式可表示成 (13) s-σ+τ 根据式(8)和式(9),当s-σ+τ≠tk-1时,有 b-q-1z(s). 当s-σ+τ=tk-1时,有 b-q-2z(s). 因而有z(s-σ+τ)≥b-q-1z(s).联立式(13),可知 将上式代入到(8)中,看到 令 那么下面这个不等式成立 情况Ⅱσ≤τ. 对t>t0+τ,有 又t0≥0,上面的不等式可表示成 将上式代入到(8)中,看到 令 那么下面的不等式成立 综上,此引理得证. 引理3[12]考虑脉冲微分不等式 (14) 其中0≤t0 那么不等式(14)不存在这样的解x(t)使得对t>t0,有x(t)>0且x′(t)>0. 引理4[18]p(t)是分段函数,若 (15) 则不等式x′(t)+p(t)x(t-σ)≤0无最终正解. 在下面的定理1至定理3中,假设引理1的条件都满足. 定理1假设tk+1-tk≥α>0,k=1,2,….如果 (16) 那么系统(3)的所有解都是振动的. 证明运用反证法,假设系统(3)有非振动解x(t).不失一般性,假设对任意t>t0,有x(t)>0,x(t-ρ)>0.即x(t)是系统(3)的最终正解.若x(t)是系统(3)的最终负解,根据假设知-x(t)则是系统的最终正解,证明过程相似.因而证明中不再赘述. 由引理1可知,对任意t∈(tk,tk+1],k=0,1,2,…,有z(t)>0.现考虑以下两种情况: 情况Ⅰσ≥α>0. 此时 z′(t)=-f(t,x(t-σ))≤-Lg(t)x(t-σ)≤0. (17) 将上式从tk到tk+α积分,有 又z(t)=x(t)-p(t)x(t-τ)≤x(t). 因而 (18) 由于tk-σ<η-σ≤tk+α-σ≤tk, 式(18)可表示成 如果条件(16)满足,那么将产生矛盾.此种情况下系统的所有解振动. 情况Ⅱ0<σ<α. 对式(17)从tk到tk+σ积分,又z(t)≤x(t),有 (19) 由于tk-α≤η-σ≤tk,式(19)可表示成 如果条件(16)满足,那么将产生矛盾.此时系统的所有解振动. 综上,满足定理条件的系统(3)的所有解都振动.此定理证毕. 定理2假设存在常数p∈(0,1],b>0和α>0,使得对任意t≥t0,有p(t)≥p,bk≤b和tk+1-tk≥α,其中k=1,2,….并且存在函数f(t)∈PC([t0,∞),R+),满足 (20) 其中T=max{t0+σ,t0+τ},m=min{k≥1:tk>T},且 此时,系统(3)的所有解振动. 证明运用反证法,假设系统(3)有非振动解x(t).不失一般性,假设对任意t>t0,有x(t)>0,x(t-ρ)>0.即x(t)是系统(3)的最终正解.接着,由引理2看到二阶脉冲微分不等式 (21) 另一方面,根据引理3不难看出,式(20)满足意味着不等式(21)没有这样一个解x(t),使得对t>T有x(t)>0,x′(t)>0.这产生了矛盾,也就是说系统(3)的所有解振动.此定理得证. 定理3假设存在常数b>0,使得对任意t≥t0,有bk≤b.假设tk+1-tk≥α>0,k=1,2,….如果 (22) 证明假设系统(3)有一个最终正解x(t),且对t≥T>t0有x(t)>0,x(t-ρ)>0.根据引理1知道z(t)>0且z(t)在(tk,tk+1],k=1,2,…上非增. 0=z′(t)+f(t,x(t-σ))≥z′(t)+Lg(t)x(t-σ)≥ z′(t)+Lg(t)(z(t-σ)+p(t-σ)x(t-σ-τ))≥ z′(t)+Lg(t)(z(t-σ)+p(t-σ)z(t-σ-τ)) 下面对t-σ是否为脉冲点进行讨论. 第一种情况,t-σ是脉冲点. 当τ<α时,有 0=z′(t)+f(t,x(t-σ))≥z′(t)+Lg(t)(z(t-σ)+p(t-σ)z(t-σ)), 因此 z′(t)+Lg(t)(z(t-σ)+p(t-σ)z(t-σ))≤0 (23) 有一最终正解. 当τ≥α时,至少存在[τ/α]=l个脉冲点,使得 此时 (24) 有一最终正解. 第二种情况,t-σ不是脉冲点. 当σ+τ<α时,同样得到式(23).当σ+τ≥α时,同样得到式(24). 根据引理4易知,当条件(22)满足时,式(23),(24)都没有最终正解.这产生了矛盾,也就是说假设不成立.因此,系统(3)的所有解是振动的.定理得证. 例1考虑脉冲微分方程 (25) 易见 因而,式(25)满足引理1中所有条件. 又tk+1-tk=1≥α>0,令α=1,此时ζ=min{2,1}=1. 根据定理1,知道系统(25)的所有解都振动. 例2考虑脉冲微分方程 (26) 易见 因此,引理1的所有条件都满足.令 考虑 其中G(t)的计算如下: 显然式(20)满足,从而根据定理2,知道系统(26)的所有解都振动. 例3考虑脉冲微分方程 (27) 有 此外, f(t,u)=(2+t+u2)u(1+|u|2)≥(2+t)u(1+|u|2)≥g(t)G(u),u>0. 这里g(t)=2+t.易见f(t,u)=-f(t,-u),因此引理1的所有条件都满足.对于任意的t>T,即t>6,有 根据定理3,系统(27)的所有解振动.1 引理和主要结果
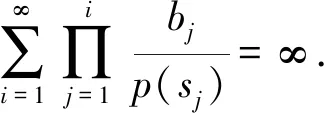

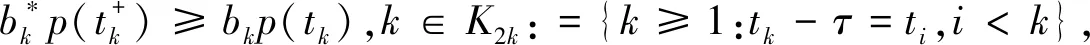




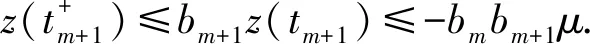
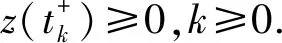
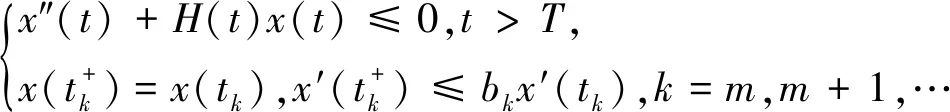
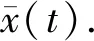

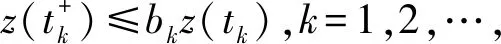
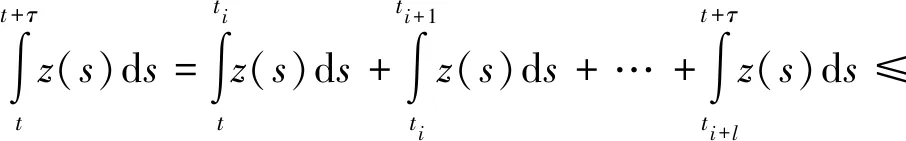

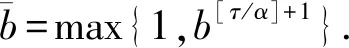


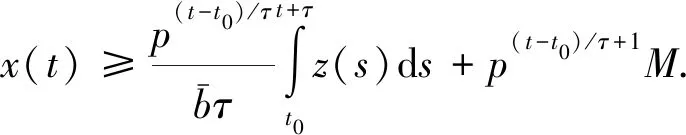


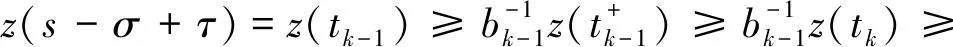





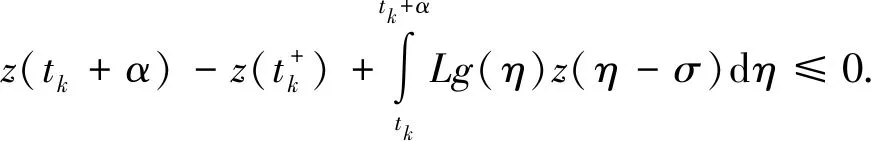


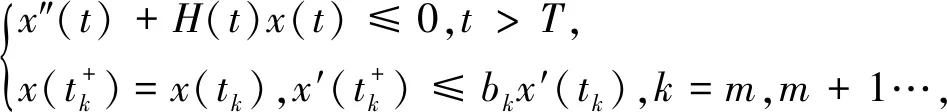



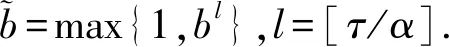
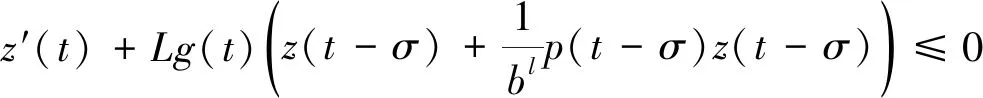
2 应用举例