非均匀锈蚀钢筋拉伸性能试验与模拟
2022-10-06李亚辉郑山锁董立国温桂峰
李亚辉, 郑山锁, 2, *, 董立国, 温桂峰
(1.西安建筑科技大学土木工程学院, 陕西西安 710055;2.西安建筑科技大学结构工程与抗震教育部重点实验室, 陕西西安 710055)
钢筋锈蚀是引发钢筋混凝土(RC)结构耐久性损伤与抗震性能劣化的主要原因[1].为评估在役RC结构的受力性能和抗震性能, 国内外学者开展了大量锈蚀钢筋力学性能研究.王波等[2]通过单调拉伸试验, 研究了锈蚀钢筋的受拉性能劣化规律, 指出锈蚀钢筋的名义本构关系与锈蚀率相关.Kashani等[3]通过试验研究, 分析了钢筋受拉性能随锈蚀程度的劣化规律, 建立了锈蚀程度与强度退化的关系, 但并未给出锈蚀钢筋本构模型参数标定理论.Almusallam等[4]基于锈蚀钢筋拉伸试验指出:钢筋的实际力学性能受锈蚀影响较小, 其名义力学性能劣化本质上是由截面积削弱引发的.因此, 科学认识锈蚀钢筋力学性能劣化机理的关键在于获取真实的钢筋锈蚀形貌.
现阶段, 国内外学者多采用质量损失率、最大截面损失率等参数来量化钢筋锈蚀程度, 量测方法也集中于失重法、游标卡尺量测法等.采用上述方法作为钢筋锈蚀程度量化指标, 虽可以在均匀锈蚀假定下近似给出钢筋名义力学性能指标的退化规律, 但并不利于深刻认识锈蚀钢筋力学性能劣化机理.近年来, 3D扫描技术作为实物立体信息转换的新兴技术, 在钢筋非均匀锈蚀力学性能研究中得到应用, 该方法采用激光扫描, 以0.02 mm精度的点云数据参数化逆向重构锈蚀钢筋的几何形貌, 从而在有限元分析软件中真实再现了钢筋非均匀锈蚀形貌, 为非均匀锈蚀钢筋的数值模拟分析及力学性能研究提供了新的技术途径.
鉴于此, 为深入研究锈蚀钢筋力学性能劣化机理与规律, 本文采用“电渗-恒电流-干湿循环”加速锈蚀方法与3D扫描技术, 获取并构建了不同锈蚀程度下、不同直径钢筋试件的非均匀锈蚀形貌, 进而通过对具有非均匀锈蚀特征的各钢筋试件进行单调拉伸试验和数值模拟, 研究锈蚀程度及钢筋直径对锈蚀钢筋力学性能的影响, 以期为在役RC结构受力与抗震能力评估提供参考.
1 试验
1.1 试件设计
非均质的混凝土材料使得侵蚀介质传输途径和输运机理存在差异, 从而导致了自然环境下混凝土内部钢筋锈蚀的非均匀性.因此, 为了获取与自然环境一致的钢筋锈蚀形态, 本文设计制作了13根不同锈蚀程度、不同直径的钢筋试件置于混凝土板件中进行加速锈蚀试验, 各试件设计参数如表1所示.混凝土采用P·O42.5R水泥配制, 设计强度等级为C40, 水灰比(质量比)为0.42.钢筋采用HRB400钢筋.通过材性试验测得混凝土立方体抗压强度为43.29 MPa, 弹性模量为30.9 GPa;钢筋的屈服强度为431.21 MPa, 抗拉强度为615.32 MPa, 弹性模量为205.0 GPa.
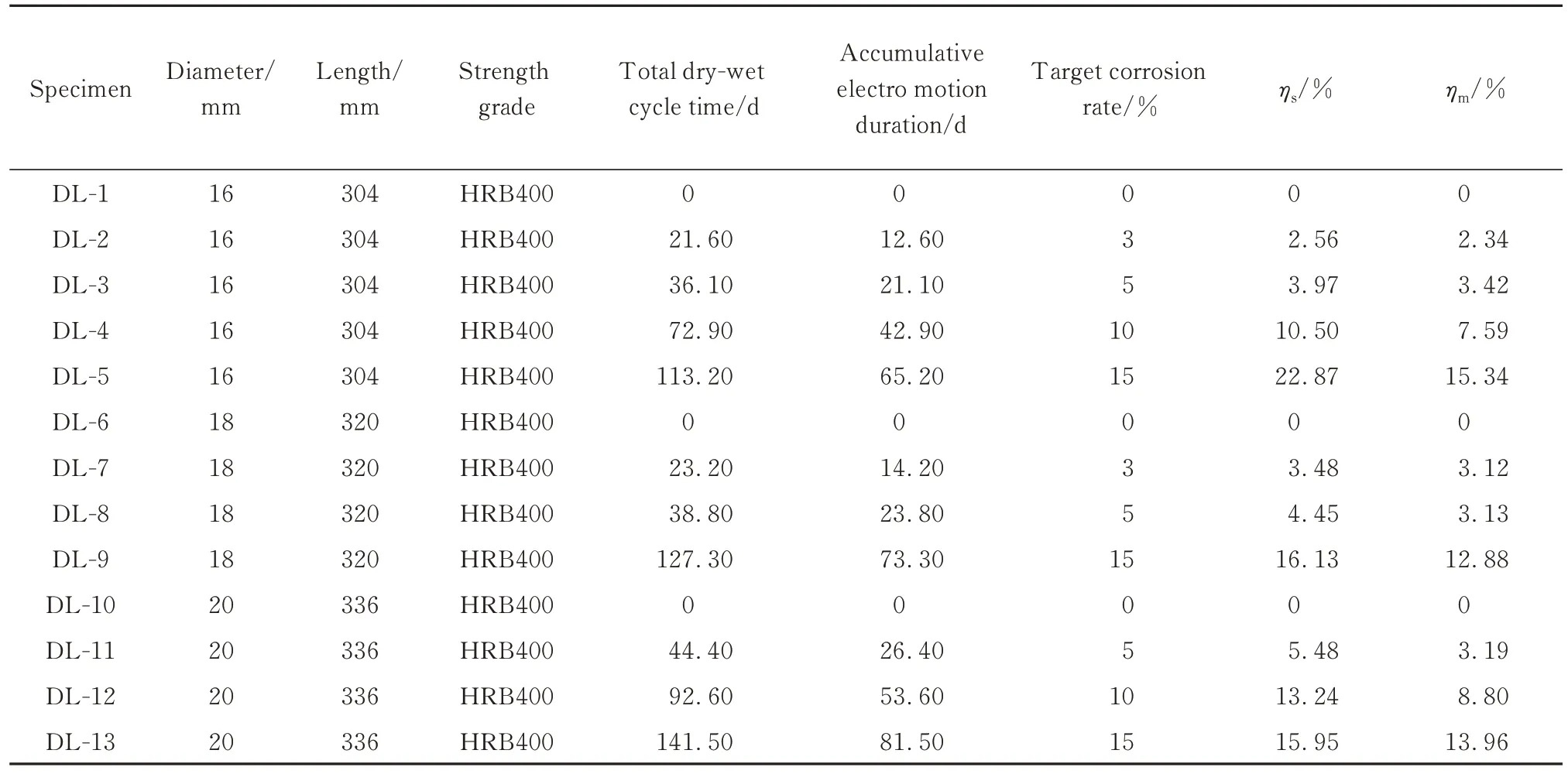
表1 试件设计参数Table 1 Design parameters of specimens
1.2 加速锈蚀方案
本试验采用金伟良等[5]提出的“电渗-恒电流-干湿循环”加速锈蚀方法, 对表1中各钢筋试件进行人工加速锈蚀试验, 锈蚀试验装置如图1所示.其中, 依据文献[5]计算可得电渗时长为48 h, 干湿循环制度为“干燥3 d, 通电4 d”.Sun等[6]的研究表明, 当锈蚀电流密度取0.1~0.5 mA/cm2时, 理论计算锈蚀率和实际锈蚀率误差小于5%.因此, 锈蚀电流密度i取0.3 mA/cm2, 累计通电时长和干湿循环总时长计算结果见表1.
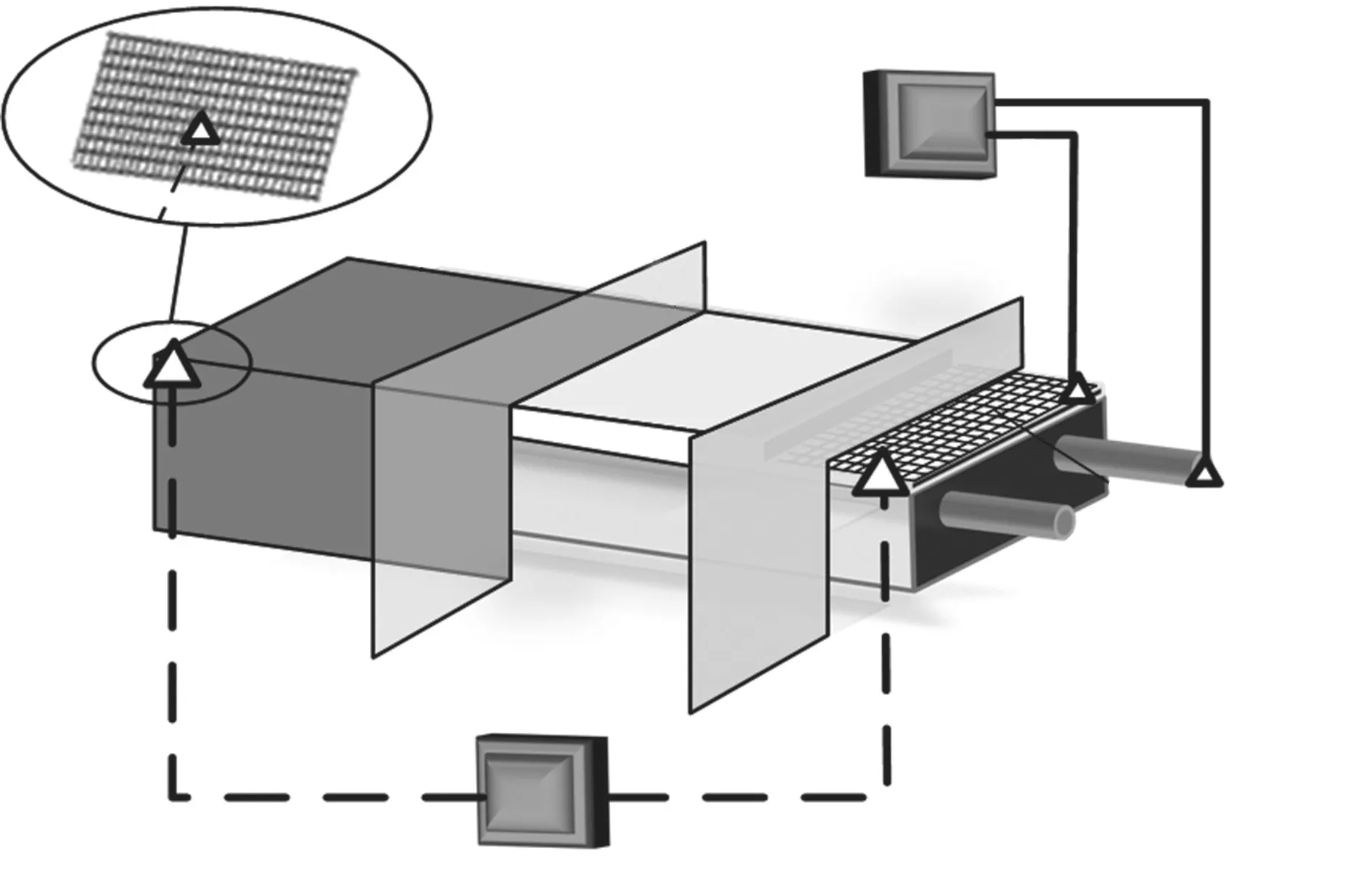
图1 加速锈蚀试验装置Fig.1 Accelerated corrosion test device
1.3 锈蚀钢筋三维模型重构试验
加速锈蚀试验完成后, 将钢筋试件从混凝土板件中取出除锈, 并使用无水乙醇清洗钢筋表面污垢, 于室内环境下充分干燥.使用精度为0.001 g的天平量测钢筋锈蚀前后的质量m0和m1, 并按式(1)计算各锈蚀钢筋的平均质量锈蚀率ηm, 结果见表1.
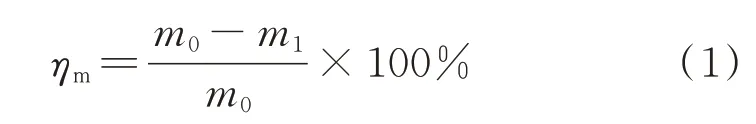
上述工作完成后, 使用精度为0.02 mm的激光扫描设备SCANTECH-900对各锈蚀钢筋试件进行3D扫描, 获取锈蚀后钢筋几何构形的点云数据, 并利用Geomagic Studio软件进行数据预处理, 去噪补缺, 保证点云数据的完整性和正确性.然后, 根据点云数据进行曲面重构, 构建锈蚀钢筋的三维虚拟模型.在Polyworks MS2020软件中将扫描结果进行三角化模型的特征抽取, 并创建沿钢筋纵向的1 mm等距离切面, 以获取其剩余截面积.按照式(2)计算钢筋最大截面锈蚀率ηs, 结果见表1.
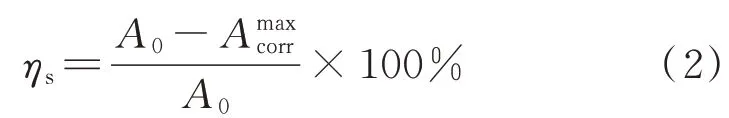
式中:A0为钢筋锈蚀前截面面积;Amaxcorr为锈蚀钢筋最大锈蚀截面面积.
1.4 加载测试
3D扫描完成后, 采用MTS 322型万能试验机对各试件进行单调拉伸试验, 锈蚀钢筋荷载-变形数据由控制系统自动采集.考虑到应变速率对锈蚀钢筋受力性能的影响, 参考GB/T 228.1—2010《金属材料 拉伸试验 第1部分:室温试验方法》, 采用等速位移控制加载方式对不同长度试件施加轴向拉力, 取不同长度试件的名义应变速率εv=6×10-5s-1, 并按式(3)计算各试件的控制加载速率κv.
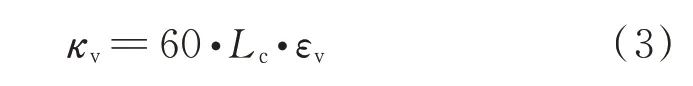
式中:Lc为试件的原始标距.
2 结果及分析
2.1 试验应力-应变曲线
根据单调拉伸试验结果, 绘制各钢筋试件荷载-位移(P-Δ)曲线, 并将各P-Δ曲线倒算为名义应力-应变(σ-ε)本构关系, 结果如图2所示.

图2 试件P-Δ曲线与σ-ε曲线Fig.2 P-Δcurves and σ-ε curves of specimens
由图2可以看出:锈蚀钢筋应力-应变曲线的名义屈服强度、名义极限强度、弹性模量等特征值均随着锈蚀率的增大逐渐降低, 名义屈服强度和名义极限强度退化率与最大截面锈蚀率增量基本相当, 各强度特征值的退化速率基本相近;硬化起始应变、名义峰值应变整体上随着锈蚀率的增加而下降, 但硬化起始应变随平均质量锈蚀率的退化速率较峰值应变更快, 且离散性较大;屈服平台长度随着平均质量锈蚀率的增加而逐渐变短直至消失, 钢筋的延性变差.对于锈蚀率相近而直径不同的试件, 锈蚀程度较小时, 直径较小的锈蚀钢筋名义屈服强度和名义极限强度退化速率更快, 受锈蚀率的影响更显著, 直径16 mm的试件DL-3和直径20 mm的试件DL-11, 在锈蚀率相近的前提下, 其名义极限强度退化量分别为32.02、9.84 MPa.其原因可能是, 直径较小的钢筋在开始锈蚀时受局部小点蚀坑引起的应力集中影响更显著.
2.2 非均匀锈蚀对钢筋力学性能的影响
采用微段切分法(见图3), 提取1.3中各1 mm等间距微段处的实际截面面积.根据式(4)依次计算不同非均匀锈蚀截面在各时刻拉力作用下的应力值σj.

图3 微段切分法示意图Fig.3 Schematic drawing of micro segmentation

式中:Pi为i时刻钢筋承受的拉力;Aj为钢筋第j段剩余截面面积.
以钢筋实际力学性能不变为前提[7], 采用完好钢筋拉伸本构模型, 按式(5)计算各截面处相应的应变值εj.

式中:f(σj)为未锈蚀钢筋本构关系的反函数.
依次计算各拉伸荷载下每个微段钢筋的变形量, 通过累加获得锈蚀钢筋的总变形量Δli, 见式(6), 进而得到锈蚀钢筋的P-Δ曲线.
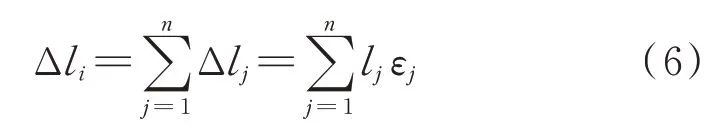
式中:Δlj、lj分别为钢筋第j段的变形量、等间距微段长度.
图4给出了由微段切分法所得各试件P-Δ曲线(derivation curve)与试验结果的对比.由图4可以看出, 钢筋的强度特征值及变形量与试验所测结果基本吻合, 只有试件DL-11强化段的强度特征值有一定误差, 这可能是由材料变异性波动造成的.因此, 锈蚀钢筋的名义拉伸力学性能退化是由钢筋各截面的削弱所致, 而其实际的材料性能未发生改变.以钢筋各截面实际剩余面积进行计算的微段切分法, 为非均匀锈蚀钢筋的强度及变形计算提供了新方法.
2.3 基于Abaqus的锈蚀钢筋模拟验证
本节基于1.3非均匀锈蚀钢筋的3D扫描模型, 通过Geomagic Studio软件进行模型文件格式转换, 获得可用于Abaqus有限元软件计算的STP格式实体模型.以1.1中未锈蚀钢筋试验数据为材料信息输入, 按照试验加载情况设置钢筋受拉段, 加载方式、加载制度以及边界条件均与试验保持一致, 采用C3D10四面体单元进行自适应网格划分, 并在局部坑蚀严重处采用较小网格进行二次划分.提取加载端耦合点的竖向位移以及固定端耦合点的反作用力, 获 得 锈 蚀 钢 筋 模 型 的P-Δ曲 线(simulation curve), 如图4所示.
由图4可知:试件DL-3、DL-9、DL-12基于实际锈蚀形态的锈蚀钢筋有限元模拟结果与试验结果吻合效果良好, 名义屈服强度、名义极限强度和弹性模量等特征值的模拟误差均在3%以内, 2条荷载-位移曲线基本重合;试件DL-5的名义极限强度在模拟时有一定偏差, 而其微段切分法结果与试验结果基本吻合, 原因可能是在实体模型转换时, 钢筋边缘处的格栅网片划分精度存在一定误差;试件DL-11的模拟结果与试验结果在强化段有约5%的误差, 而其模拟曲线与微段切分法结果差异较小, 其原因可能为完好钢筋材料的性能具有变异性.综上, 基于实际锈蚀形态的锈蚀钢筋有限元模拟结果与试验结果基本吻合, 各特征值的模拟结果基本与试验结果一致, 该方法可以较好地模拟非均匀锈蚀钢筋的力学性能.
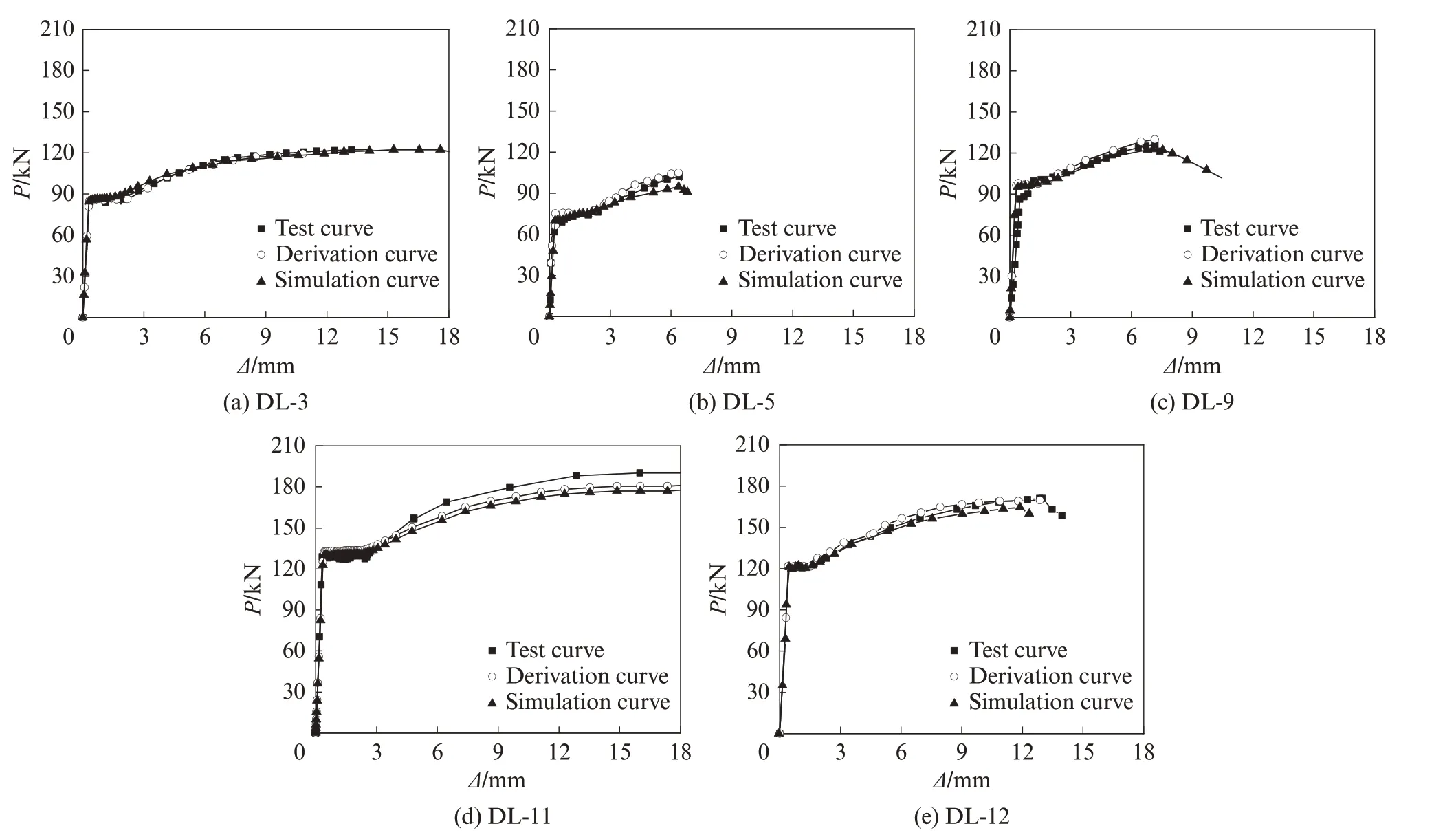
图4 锈蚀钢筋荷载-位移曲线对比Fig.4 Comparison of P-Δcurves of corroded steel bars
3 锈蚀钢筋拉伸本构模型的建立及验证
现阶段, 关于完好钢筋拉伸本构模型的研究已相对成熟, 可考虑钢筋单调加载时的屈服、硬化和软化等行为, 并已集成于OpenSees等软件实现程序化.而锈蚀钢筋本构模型因受限于锈蚀方法不同以及锈蚀随机性的影响, 导致其计算精度和通用性较差.鉴于此, 本文收集了部分既有锈蚀钢筋拉伸试验数据[6-7, 9-13](见表2), 以适用性较好的未锈蚀钢筋单调拉伸本构模型[8]为基础, 对相应模型参数进行锈蚀率影响修正, 从而建立以最大截面锈蚀率、平均质量锈蚀率为锈蚀程度量化指标的锈蚀钢筋拉伸本构模型.

表2 既有锈蚀钢筋拉伸试验数据Table 2 Summary of tensile data of corroded reinforcement
3.1 锈蚀钢筋拉伸本构模型的建立
为建立平均质量锈蚀率ηm与最大截面锈蚀率ηs的关系, 将Sun等[6]、罗小勇等[7]及本文所测数据绘制于图5(a)中.由图5(a)可以看出二者基本服从线性关系.因此, 采用线性拟合建立2种不同锈蚀程度量化指标的关系, 结果如式(7)所示.

由前文可知, 锈蚀钢筋名义本构模型的各强度特征值退化程度受锈蚀较大的最不利截面影响, 可选取最大截面锈蚀率ηs作为钢筋锈蚀程度量化指标, 来表征锈蚀钢筋名义屈服强度fyη、名义极限强度fsη和名义弹性模量Esη等强度特征值的退化规律.各变形特征值与沿钢筋纵向的坑蚀分布有关, 但考虑到现在还没有精度较高的量化钢筋纵向非均匀锈蚀分布的方法, 同时考虑到工程实际的可行性、钢筋材料的变异性以及锈蚀的随机性, 仍以平均质量锈蚀率ηm来表征锈蚀钢筋硬化起始应变εpη和名义峰值应变εsη等变形能力的退化.采用式(7)将所收集的不同锈蚀程度量化指标试验数据进行转换, 并将各特征值与锈蚀率的关系绘于图5(b)~(f).
由图5(b)~(f)可知:各应力-应变特征值均随最大截面锈蚀率ηs、平均质量锈蚀率ηm的增加而发生不同程度的退化, 总体退化趋势为线性衰减;其中各试验结果的名义屈服强度fyη和名义极限强度fsη均随着最大截面锈蚀率ηs的增加而表现出更好的线性退化趋势;变形特征值因材料本身的变异性及锈蚀的不确定性而表现出相对离散的线性退化趋势.

图5 钢筋名义本构模型特征量与锈蚀率的变化规律Fig.5 Variation of characteristic parameters of nominal constitutive model and corrosion rate of steel bar
为便于本构模型的应用, 采用线性拟合建立各锈蚀钢筋试验结果的名义屈服强度fyη、名义极限强度fsη、名义弹性模量Esη、硬化起始应变εpη、名义峰值应变εsη与最大截面锈蚀率ηs、平均质量锈蚀率ηm的关系, 结果如式(8)所示.

式中:fy0、fs0、Es0、εp0、εs0分别为未锈蚀钢筋的名义屈服强度、名义极限强度、名义弹性模量、硬化起始应变和名义峰值应变.
将前述以最大截面锈蚀率ηs、平均质量锈蚀率ηm为参数标定的各特征值退化关系引入到未锈蚀钢筋本构模型[8]中, 并对模型参数进行锈蚀率影响修正, 其中k1η为锈蚀钢筋名义硬化起始应变与名义屈服应变的比值;k2η为锈蚀钢筋名义峰值应变与名义屈服应变的比值;k4η为锈蚀钢筋名义极限强度与名义屈服强度的比值.将修正后的各参数代入, 得到锈蚀钢筋拉伸本构模型, 如式(9)所示.
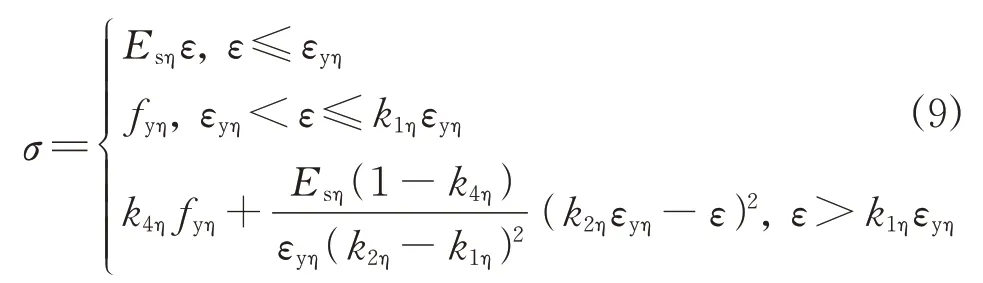
3.2 锈蚀钢筋拉伸本构模型的验证
采用本文试件DL-2、DL-8、DL-11、DL-12以及Sun等[6]、Imperatore等[11]的部分试验数据, 对所建立的锈蚀钢筋拉伸本构模型进行验算分析, 所得验算曲线与试验曲线的对比如图6所示.从图6可以看出:基于最大截面锈蚀率修正的名义屈服强度和名义极限强度等强度特征参数吻合较好, 试件DL-2、DL-8的名义屈服强度和名义极限强度的计算误差分别为-1.203%、-1.122%、0.516%、-0.965%;Sun等[6]、Imperatore等[11]部分数据在极限强度的模拟时有一定偏差, 这是由加速锈蚀方法和试验条件不同以及因锈蚀率增大使得钢筋力学性能不稳定所致, 但计算误差基本在8%以内.这说明以最大截面锈蚀率为锈蚀程度量化指标计算锈蚀钢筋的强度退化较为准确可行.由图6还可见, 基于平均质量锈蚀率的本构模型应变特征值计算结果与试验结果稍有误差, 推测其原因为:随着锈蚀率的增大, 钢筋截面削弱严重, 屈服台阶逐渐变短, 力学性能不稳定.但误差基本在15%以内且曲线相对吻合较好.综上, 本文建立的锈蚀钢筋拉伸本构模型验算结果与试验结果吻合良好, 模型准确性较高.
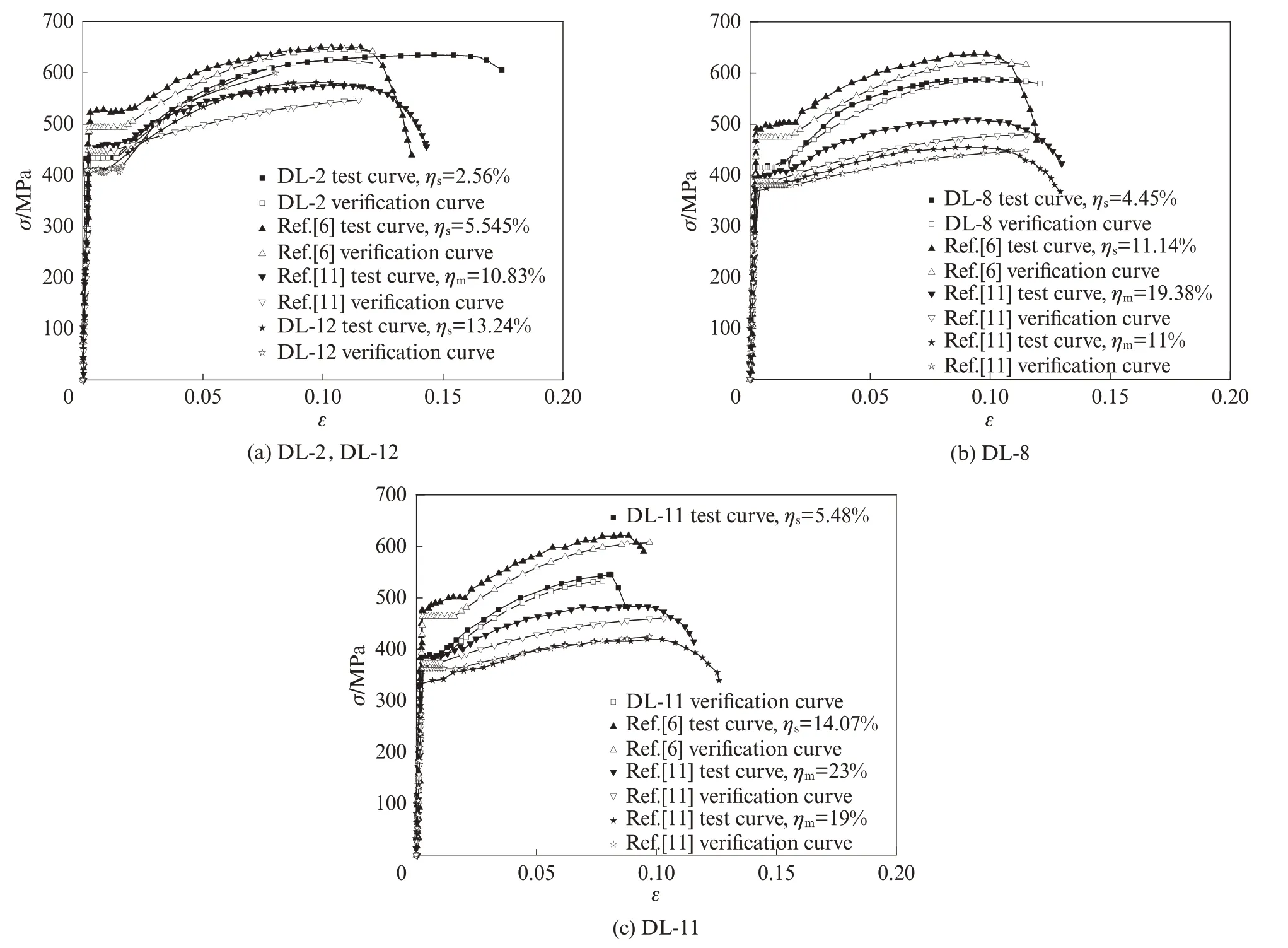
图6 锈蚀钢筋拉伸本构曲线验证Fig.6 Validation of tensile constitutive curve of corroded steel bars
4 结论
(1)锈蚀钢筋的名义屈服强度、名义极限强度、名义弹性模量均随最大截面锈蚀率的增大而呈线性退化趋势, 且退化率与最大截面锈蚀率增量基本相当, 各强度特征值退化速率基本相近.
(2)基于3D扫描技术获得非均匀锈蚀钢筋的真实形貌, 采用微段切分法证明了锈蚀钢筋拉伸力学性能的退化主要是由锈蚀造成的钢筋横截面积的削弱引发, 而其实际力学性能并不发生改变.
(3)基于已有试验数据, 建立了最大截面锈蚀率与平均质量锈蚀率的关系, 且定量描述了各特征值随锈蚀率的退化规律, 建立了锈蚀钢筋拉伸本构模型, 为在役钢筋混凝土结构的受力与抗震能力评估提供了参考.
